贝叶斯最优多阶段Ⅱa期自适应临床试验方法-BOP2设计

谢婉秋, 周 影， 郭东升

(1.黑龙江大学 数学科学学院, 哈尔滨 150080; 2.哈尔滨金融学院 投资保险系, 哈尔滨 150030;3.科临达康医药生物科技(北京)有限公司 生物统计与编程部门, 北京100026)

0 引 言

Ⅱ期临床试验的目的是评估新疗法的初步疗效，并确定这种疗法是否有进行大规模的Ⅲ期随机对照临床研究的研发前景[1]。其中Ⅱa期临床试验的基本设计特征是早期无效终止和中期go/no-go决策，防止过多的患者暴露在可能无效的治疗中[2]。已经有众多的频率设计和贝叶斯设计应用于国内外Ⅱa期临床试验[3-12]。目前国内的临床研究中，尤以著名的频率设计Simon两阶段设计应用最为广泛[13-14]，它在治疗是无效的原假设下，给定Ⅰ类和Ⅱ类错误率，可最大程度地减少期望的样本量或最大样本量。如果想多做几次中期观察，统计师也可参考其他相关研究包括Fleming的多阶段检验[15]、Ensign的最优三阶段设计[16]和Chen的最优三阶段设计[17]等。

另一面，以贝叶斯设计的观点来看，无效监测的一种方式是基于感兴趣事件的后验概率做出go/no-go的决策。Thall等基于这种思想，提出了一种贝叶斯Ⅱa期设计，如果中期数据表明治疗的缓解率有很高的概率小于预先指定的临界值，则终止试验；否则进入下一个中期观察。此方法原理直观，已在美国MD Anderson等癌症中心广泛使用[18]。在后验概率的基础上，Heitjan提出使用“说服概率”判断新疗法是否具有研发前景[19]。Tan等提出了两个贝叶斯两阶段设计，他们模拟了频率学派的多阶段设计[20]。Cai等提出可以通过使用多重插补方法处理延迟的疗效结局[21]。Lee等提出了另外一种基于预测概率的贝叶斯Ⅱa期设计，可以根据任意时刻的中期数据对最终数据进行预测并计算最终试验成功的概率[22]。然而，以上无论基于后验概率还是预测概率的设计大都集中在一个二元疗效终点，如客观缓解率，但随着新型分子靶向药物和免疫疗法的出现，主要终点变得更加复杂，可以是有序的或多变量的[23]。

以下列举了常见的四种不同类型终点的Ⅱ期试验，BOP2设计将采用统一的模型处理以下Ⅱ期设计。

例1. 二元疗效终点：一个Ⅱ期临床试验，目的是评估二甲双胍在复发性小细胞肺癌患者的疗效[24]。主要终点是ASO治疗复发性SCLC患者的客观缓解率(ORR)(使用RECIST1.1版[25]定义)。根据历史数据，原假设ORR≤5%，成立则认为治疗无效，备择假设ORR≥20%，成立则认为该疗法具有研发前景。该示例用于说明具有二元疗效终点的标准情况。

例2. 嵌套的疗效终点：一个Ⅱ期临床试验，目的是评估一种新型人源化单克隆抗体对自体干细胞移植后失败的霍奇金淋巴瘤患者的疗效。采用修订后的《国际恶性淋巴瘤工作组标准》[26]定义淋巴瘤治疗的有效性，从四种降低水平分类中选取一种，包括完全缓解(CR)，定义为所有疾病证据的消失；部分缓解(PR)，定义为可测量病灶的消退，没有新病灶；疾病稳定(SD)，定义为未达到CR、PR或疾病进展(PD)的标准；疾病进展(PD)，定义为任何新病变的证据或病变体积从先前受累部位的最低点增加了50%。在该试验中，尽管CR和PR均被认为是有利的疗效反应，但实际上CR更可取。原假设是Pr(CR+PR)≤30%且Pr(CR)≤15%，成立则认为治疗无效。备择假设Pr(CR+PR)≥50%或Pr(CR)≥25%，成立则该认为该疗法具有研发前景，其中第二种条件的终点嵌套在第一种条件终点中。

例3. 共同多疗效终点：一个Ⅱ期临床试验，方案名为GOG 0229E，主要目的是研究贝伐单抗对复发或持续性子宫内膜癌患者的疗效。该试验有两个共同的主要疗效终点：客观缓解率(ORR)和6个月无疾病进展(或死亡)生存的概率(PFS6)。客观缓解率使用RECIST 1.1[25]定义。无进展生存期(PFS)定义为从治疗开始到发生疾病进展或任何原因死亡的时间。原假设是ORR≤10%且PFS6≤15%。成立则认为治疗无效。两个指标在临床显著改善的差异为20%，所以备择假设ORR≥30%或PFS6≥35%，成立则认为该疗法具有研发前景。

例4. 联合监测疗效和毒性终点：一个Ⅱ期临床试验，主要目的是评价低剂量氯法拉滨和阿糖胞苷联合治疗复发或对低甲基化药物不敏感的高危骨髓增生异常综合征患者的疗效[27]。主要疗效终点是使用2006年修正的国际工作组标准定义的CR率联合监测治疗的安全性，以与研究药物相关的3级毒性率作为联合终点。原假设是CR率≤20%或毒性率≥30%，成立则认为治疗无效。如果CR率>20%且毒性率<30%，则认为该疗法具有研发前景。

本文重点介绍Zhou等2017年提出的一种灵活的贝叶斯最优Ⅱ期(BOP2)设计，该设计能够处理上述试验场景[1]。BOP2设计使用Dirichlet-多项式模型处理不同类型的终点。在每个中期阶段，通过评估事件的后验概率来做出go/no-go的决策。BOP2设计可精确控制Ⅰ类错误率，在某种意义上是最优的，包括在固定样本量的备择假设下优化检验效能或在原假设下最小化期望样本量。Thall等提出了针对多主要终点(例如毒性和疗效)的贝叶斯序贯监测设计[28]。与这些设计相比，BOP2设计具备更多的优势，包括：(1)提供一个更灵活的框架来同时监测多个事件，包括嵌套或共同主要终点；(2)精确控制Ⅰ类错误率并优化特定的目标函数，从而弥补贝叶斯设计与频率设计之间的差距，使所提出的贝叶斯优化设计更易于为广大用户和监管机构所用；(3)模拟研究表明，允许终止规则的临界值随中期样本量发生变化，从而提高设计的检验效能。

本文第1节详细介绍BOP2设计的概率模型，描述了试验设计和设计参数的优化；第2节实际临床试验案例分析，同时简要介绍www.trialdesign.org网站实现BOP2设计的软件操作；第3节采用模拟方法比较BOP2与其他贝叶斯Ⅱ期设计的优势，最后给出结论。

1 方 法

1.1 概率模型

尽管上述四个试验案例的主要终点采用不同的形式，但可以统一由服从多项式分布的随机变量X和K个类别表示：

X～Multinom(θ1,…,θk)

(1)

式中θk=Pr(X=k)是X属于第k个类别的概率，k=1,…,K。K个类别可以是单个终点的真实级别，也可以是多个真实类别终点的某种组合。如例1中单个二元疗效终点，多项式的分类K=2(OR，无OR)。例2中，X是有序结局指标，X=1,2,3和4分别表示CR，PR，SD和PD。例3中，X是具有4个类别的多项式变量：1 =(OR，PFS6)，2 =(OR，无PFS6)，3 =(无OR，PFS6)和4 =(无OR，无PFS6)。例4中，X是具有4个类别的多项式变量：1 =(毒性，CR)，2 =(无毒性，CR)，3 =(毒性，无CR)和4 =(无毒性，无CR)。

例1中N次抽样(即N个患者参与试验)，X为缓解的人数，服从二项式分布；类似的，例2、3、4将试验结局分为4组，4组中结局发生对应的概率分别为θ1,θ2,θ3,θ4，且θ1+θ2+θ3+θ4=1；用(X1,X2,…,Xn)分别表示N个患者中每个结局组的人数，则X=(X1,X2,…,Xn)服从多项式分布，可见例1为例3的特例，如果例3忽略PFS6，多项式分布则退化为二项式分布。

设b表示由元素0和1组成的设计向量，而在以上4个示例中中期观察的有效性可以表示为模型参数θ=(θ1,…,θk)T的线性组合：bθ≤φ或bθ≥φ，其中，φ代表预先指定阈值。

具体例1中，H0:bθ≤φ，其中b=(1,0)，φ=0.05；例2和例3中，H0:b1θ≤φ1且b2θ≤φ2，其中例2中b1=(1,0,0,0),b2=(1,1,0,0),φ1=0.15,φ2=0.3；例3中b1=(1,1,0,0),b2=(1,0,1,0),φ1=0.1,φ2=0.15；例4中，H0:b1θ≤φ1或b2θ≥φ2，其中b1=(1,1,0,0),b2=(1,0,1,0) ,φ1=0.2,φ2=0.3。以上结果汇总在表1中。

表1 四个试验案例的结局及参数设置Table 1 Outcome and parameter setting of four trail cases

在贝叶斯的框架下，通常为了方便推导参数的后验分布，会先假设参数的先验分布是联合似然函数的某个共轭分布，故假设θ=(θ1,…,θk)T服从Dirichlet共轭先验分布：

θ～Dirichlet(α1,…,αK)

(2)

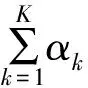
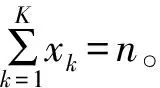
θ|Dn～Dir(α1+x1,…,αK+xK)

(3)

在X是二元结局的特例中(例1)，该Dirichlet-多项式模型退化为标准的Beta-二项式模型。

1.2 试验设计

设N代表试验的最大样本量。BOP2设计包括R个中期观察，当纳入的患者人数达到n1,n2,…,nR时，以及所有N个患者都纳入后的最后一次观察。如下文所述，每一次中期观察的目的包括评估新疗法是否具有研发前景或者由于目前试验累积的数据不足以支持任何结论而需要纳入更多的患者。换言之，患者分别纳入到大小为n1,n2-n1,…,N-nR的R+1队列中，并在每个队列入组后做出go/no-go的决策。当R=N-1时，获得了一个完整的序贯设计，在每个患者之后都会连续评估go/no-go决策。

设C(n)表示概率阈值，它是中期样本量n的函数。在这个设计中，每个中期阶段的go/no-go决策都是基于事件的后验概率来进行的。具体地，对于四个试验案例，在中期观察后，如果出现以下情形则终止试验：

例1： Pr(θ1≤0.05|Dn)>C(n)；

例2： Pr(θ1≤0.15|Dn)>C(n)且Pr(θ1+θ2≤0.3|Dn)>C(n)；

例3： Pr(θ1+θ2≤0.1|Dn)>C(n)且Pr(θ1+θ3≤0.15|Dn)>C(n)；

例4： Pr(θ1+θ2≤0.2|Dn)>C(n)或Pr(θ1+θ3≥0.3|Dn)>C(n)。

与大多数现有的贝叶斯设计[18,28]假定一个恒定的临界值不同，BOP2设计的作者们允许概率阈值C(n)是中期样本量n的函数。就像优化参数设计中展示的内容，这种修改可以大大提高设计的检验效能，是BOP2设计的点睛之笔。尽管这些停止规则在临床上有不同的解释，但是go/no-go决策都是可归结为基于对模型参数θ=(θ1,…,θk)T的线性组合的后验概率为评估基础，例如，

Pr(bθ≤φ|Dn)>C(n)

(4)

式中b是元素为0和1的设计矢量，φ是预定阈值。

Dirichlet分布有两个特性有助于对(4)中的后验概率进行评估。

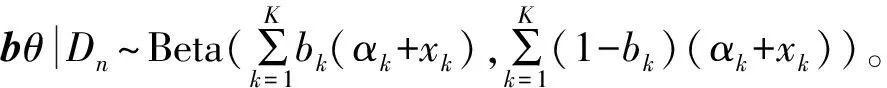
因此，可以将Pr(bθ≤φ|Dn)很容易地评估为

式中B(φ;ζ,ξ)是含有参数ζ和ξ的Beta分布的累积分布函数，并评估值φ。Pr(bθ≤φ|Dn)的性质导致以下结果。

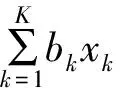
性质1和引理1的证明和解释过程见附件1。在实践中，Pr(bθ≤φ|Dn)的单调性很重要，由于单调性，不需要在搜索网格中的每一个点上执行实时计算，可在试验开始前，通过单调性来计算停止边界，这类似于Simon的两阶段设计。表2展示了在控制Ⅰ类错误率10%，已知最大样本量40，最大化检验效能的条件下，四个试验案例的停止边界。如例1中25例患者入组以后，如果缓解的患者数≤1则终止试验，判断新疗法没有研发前景；例2中，纳入25例患者后，如果CR人数≤4且CR+PR人数≤8则终止试验，判断新疗法没有研发前景。这个过程不需要任何复杂的计算，仅需计算相关的事件数，便可以做出go/no-go的决策，表2中数据可以在www.trialdesign.org网站获得，仅需输入几个简单的参数。这个属性使BOP2设计在实践中非常容易实现。

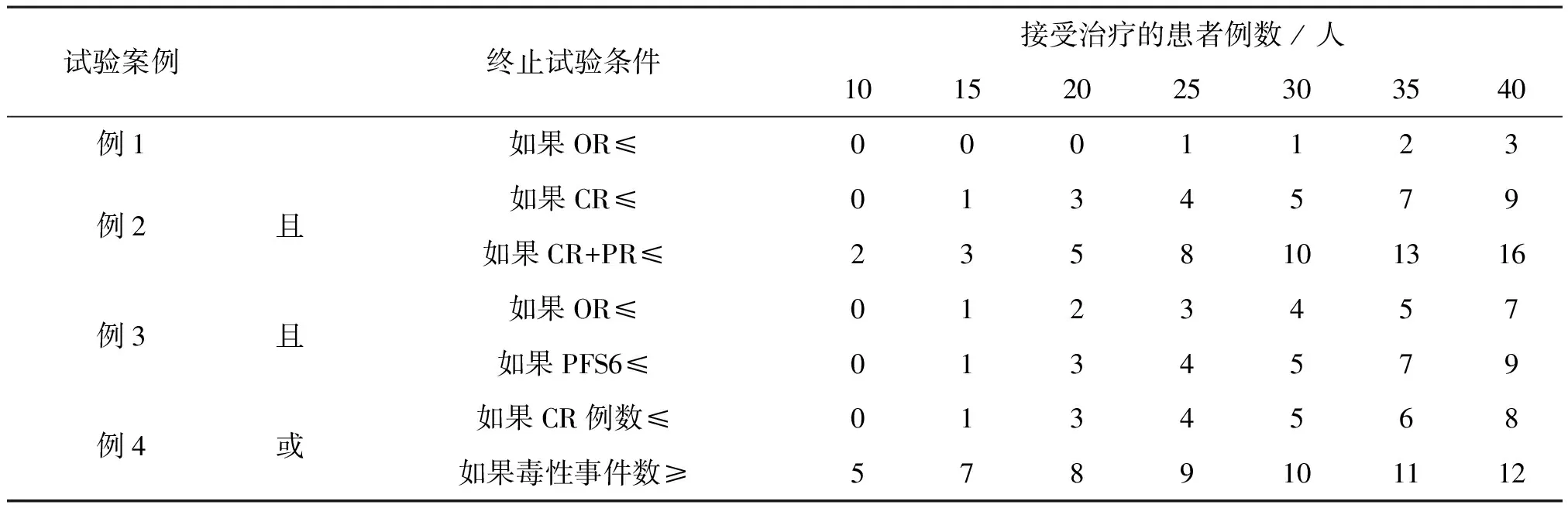
表2 四个试验案例的BOP2设计的停止边界值Table 2 Stop boundary value of BOP2 design of four trail cases

1.3 优化设计参数

首先，本设计需根据相关试验背景选择适当的原假设H0和备择假设H1，依据反证思想，原假设为希望依据数据拒绝的假设。原假设表示的θ认为该方法无效，而备择假设为希望得到的结论，即表示的θ认为该疗法有研发前景。Ⅰ类错误率和统计检验效能分别定义为在H0和H1下拒绝H0的概率，Ⅰ类错误率是指药物无效的原假设为真时拒绝原假设的概率，应使其得到有效控制即保证患者风险最小化;统计检验效能是指该疗法具有研发前景的备择假设为真时拒绝原假设的概率，应尽量在控制风险的前提下最大化检验效能以保证新药申办者的利益。如例2中，H0：θ1≤0.15和θ1+θ2≤0.3，一个可能的合理备择假设是H1：θ1≥0.25或θ1+θ2≥0.5。对于这种复杂的终点，H0和H1的预定阈值应通过与临床医生协商确定，用来反映在临床实践中可行的理想结果。未拒绝H0意味着试验结果未达到最低临床有效边界值，则该疗法无效，不具有研发前景。

与大多数贝叶斯设计假定一个恒定的临界值不同，BOP2设计的点睛之笔在于指定的一个概率阈值是中期样本量n的函数C(n)，这种修改可以大大提高设计的检验效能。C(n)可以使用任何灵活且合理的单调递减函数，但采用如下两参数幂函数可以具有良好的特性：

C(n)=1-λ(n/N)γ

(5)

其中λ和γ是调整参数。要求γ> 0，以便C(n)随着n/N单调递减，这样设计的优点是试验开始时数据比较稀疏，停止规则较为严格，避免意外终止，随着越来越多的数据积累，对目标终点的不确定性越来越小，停止规则自适应地变得更加宽松。为获得最优解，BOP2提出者设定了两种方式优化准则，在各类限制条件下的所有解中选取最合适的一组。

1.3.1 固定最大样本量和Ⅰ类错误的条件下最大化检验效能

在固定样本数量N时，通过选择调整参数λ和γ，将Ⅰ类错误率控制在特定的预定水平下(例如10%)最大化检验效能。按以下步骤进行：

步骤1： 从临床医生得到H0和H1，从申办方得到最大样本量，从监管机构得到Ⅰ类错误率。

步骤2： 找到控制的Ⅰ类错误率以下的所有(λ,γ)值，可以通过数值网格搜索来执行。

步骤3： 在步骤2中确定的(λ,γ)集合中，选择产生最大统计检验效能的集合作为最佳设计参数。

尽管BOP2设计是贝叶斯设计，但仍然必须确保设计具有所需的频率学特性[29](例如Ⅰ类概率和检验效能)。可控制的Ⅰ类错误率，能弥补贝叶斯设计和频率设计之间的鸿沟，使BOP2设计可供众多用户和监管机构使用。

1.3.2 控制Ⅰ类和Ⅱ类错误的条件下最小化期望样本量

另一种优化策略是给定预定的Ⅰ类和Ⅱ类错误率，选择λ和γ，在原假设为真的条件下，将样本量N的期望值E(N|H0)最小化。Simon的二阶段最优设计使用了这种优化标准。在这种方法中，不固定N，但是要优化设计参数，确定使E(N|H0)最小的(λ,γ,N)值，过程可以描述如下：

步骤1： 从临床研究者得到H0和H1，选择申办方可接受的Ⅱ类错误率，从监管机构得到Ⅰ类错误率。

步骤2： 找到控制的Ⅰ类和Ⅱ类错误率以下的(N,λ,γ)值，可以通过数值网格搜索来执行。

步骤3： 在步骤2中确定的(N,λ,γ)集合中，选择产生最小E(N|H0)的集合作为最佳设计参数。

在第2步中，有两个约束条件(即Ⅰ类和Ⅱ类错误率)，但需要确定三个未知参数(N,λ,γ)的值。因此，原则上会得到无穷多个解。通过将N值限制在(Nmin,Nmax)范围内可以解决此问题，其中Nmax是在实践中可以提供的最大样本量，由预算、增长率或其他实际因素决定。Nmin是试验的最小样本量，只要合理小(例如Nmin= 10)，就不会对设计的操作特性产生影响。给定N的特定值，基于两个约束的网格搜索，可以唯一地确定λ和γ的值。此优化策略的一个潜在限制是无法直接控制样本量N，并且在某些情况下，对于实际使用而言，使E(N|H0)最小的N值可能过大。因此，建议采用固定最大样本量和Ⅰ类错误的条件下最大化检验效能的方法计算合理的样本量。

2 实际案例分析

2.1 研究设计

根据文献报道，一项注册研究(NCT01210222)，试验方案为每周静脉注射15 mg·kg-1的特雷班尼布对持续或复发子宫内膜癌患者的疗效[30]，与很多处于Ⅱ期的癌症患者一样，这些患者的特点是病情进展迅速，对新增化疗药不敏感。该试验有两个共同的主要疗效终点：客观缓解率和6个月无事件生存期。客观缓解率使用RECIST 1.1[25]定义。无事件生存期(EFS)定义为从治疗开始到首次发生任何事件的时间，包括疾病进展而无法进行手术治疗、局部或远处复发、任何原因导致的死亡等。这两个终点都值得Ⅱ期研究中进一步探讨，因为他们都有望成为总生存期(OS)的有效替代终点。

本研究的原假设H0的界值是根据基于相似人群的历史数据集获得，H0联合规定ORR≤10%且EFS6≤20%，成立则认为治疗无效。临床上显著差异是指6个月无事件生存期发生率增加20%，或客观缓解率提高15%。所以，备择假设EFS6≥40%或ORR≥25%，成立则认为该疗法具有研发前景。

2.2 Web端软件操作

操作界面友好，非统计专业人员也能熟练操作和理解，本节将演示2.1节的试验案例软件操作，用户仅需选择试验主要终点的类型，中期观察及最大样本量，有效率或毒性率，Ⅰ类及Ⅱ类错误率等参数，即获得试验停止边界的表格(结果见表3)，与Simon两阶段法设计类似，BOP2设计的一个重要的优点是试验开始之前便可在试验方案中列出停止边界值，在试验进行中，无需统计专业人员干预，研究者仅需计算出相关事件的数量，通过查表(表3)观察是否超出边界便可做出go/no-go决策。网站www.trialdesign.org免费开放，无需注册。

表3 试验案例NCT01210222的BOP2设计的停止边界值Table 3 Stop boundary value of BOP2 design of trail case NCT01210222

2.3 研究结果

采用BOP2设计方法，在控制Ⅰ类错误率10%，已知最大样本量55的条件下，对比文献中两阶段法，本方法可中期观察多次，以观察4次举例，结果见表3：入组28例患者中，至多2名患者获得客观缓解(CR或者PR)或者至多5名患者获得6个月无事件生存期，则试验终止，定论试验药物没有研发前景；入组35例患者中，至多4名患者获得客观缓解(CR或者PR)或者至多7名患者获得6个月无事件生存期，则试验终止，定论试验药物没有研发前景；入组48例患者中，至多6名患者获得客观缓解(CR或者PR)或者至多12名患者获得6个月无事件生存期，则试验终止，定论试验药物没有研发前景；入组55例患者中，至多9名患者获得客观缓解(CR或者PR)或者至多15名患者获得6个月无事件生存期，则试验终止，定论试验药物没有研发前景。考虑两个终点正相关，该项研究检测出临床显著效果的检验效能(把握度)是99.13%，显著高于文献中两阶段法的90%～92%的检验功效。

3 模拟研究

本节介绍原文中的模拟比较结果并给予充分解释。BOP2作者通过模拟方法比较了BOP2与文献中其他贝叶斯Ⅱ期设计，在模拟研究中，所有设计的Ⅰ类错误率控制在10%。下面将重点讨论最大化检验效能的BOP2设计，最小化期望样本量E(N|H0)可查阅文献深入学习。在治疗首个10例患者后进行了中期分析，以后每增加5例有结局患者后观察一次，最大样本量N=40。

在每个场景下模拟10 000次试验，通过三个指标评估不同设计方法的性能：(1)拒绝无效假设(PRN)的百分比：定义为拒绝H0的模拟试验的百分比。当H0为真时，PRN为Ⅰ类错误率；当H1为真时，PRN为统计检验效能。PRN也可以解释为新疗法有效的百分比；(2)提早终止概率(PET)的百分比：定义为提早终止的试验的百分比；(3)实际样本量：定义为10 000个模拟试验中实际使用的平均样本量。

3.1 二元疗效终点

对于简单的二元疗效结局(即OR/无OR)，如试验案例1构建了四对不同原假设H0和备择假设H1的场景，并比较BOP2设计与Thall等提出的贝叶斯设计[8](简称为TS设计)，两个设计主要的区别在于定义临界值的方式不同(TS设计使用固定临界值C，而BOP2设计使用适应性概率阈值C(n))。表2列举出了BOP2设计的停止边界值，以中期观察到的有效的患者例数为依据，这些有效的患者用于在表4中场景1的每一次中期分析时做出go/no-go 决策。表4显示了ORR的四对不同H0和H1的场景下，两种设计的性能，分别列出4个场景下的PRN、PET和实际样本量，模拟结果可得到BOP2设计产生的检验效能比TS设计大得多。例如，场景2中，原假设ORR为20%，备择假设ORR为40%，当真实ORR为40%时，BOP2设计的检验效能为88.3%，而TS设计的检验效能仅为76.4%。此外，与TS设计相比，BOP2设计在新疗法有效时错误地终止试验的风险较小。例如，当真实ORR为40%时，TS设计错误地终止了23.5%的试验，而BOP2设计错误地终止了11.4%的试验。

表4 试验案例1二元疗效终点中BOP2和TS设计PRN、PET及实际样本量模拟结果比较Table 4 Comparison of BOP2 and TS design PRN, PET and actual sample size simulation results in the binary efficacy endpoint of trail case 1

在原假设下，TS设计比BOP2设计更有可能终止试验。因为TS设计有终止试验的高趋势，所以它的实际样本量比BOP2设计小。由于观察到的数据具有离散性，并且定义临界值的方式不同，在某些场景下，不可能将两种设计的Ⅰ类错误率精确匹配到10%。这就解释了在场景1中，TS设计的Ⅰ类错误与BOP2设计相等，而在场景2中，则略高。

3.2 嵌套的疗效终点

表5显示了在试验案例2的嵌套疗效终点的模拟结果，表2给出了相应的停止边界值。最初的10名患者入组后开始中期观察，然后每5名患者入组后进行中期监测。情景1是原假设，即H0:Pr(CR)≤0.15和Pr(CR+PR)≤0.3，情景7是备择假设，即H1:Pr(CR)≥0.25或Pr(CR+PR)≥0.5。同样将BOP2设计与TS设计进行比较，如表5所示，BOP2设计通常比TS设计具有更大的检验效能。如在场景7中，Pr(CR)=0.25,Pr(CR+PR)=0.5，则BOP2设计的检验效能为85.5%，而TS设计的检验效能仅为74.2%。比较这两种情况，观察到当真实的CR率从15%增加到20%时，BOP2设计可以将PRN从8.7%增加到24.2%。这恰好满足了可以对BOP2设计的期望，该设计可以同时监测嵌套的终点。相反，TS设计无法区分这两种情况，因为CR+PR比率均为30%。另外，当治疗实际上有效时，TS设计比BOP2设计倾向于更大的概率错误终止试验。如在场景7中，TS设计提前25.7%的时间终止了试验，而BOP2设计提前了9.9%的时间终止了试验。同样，由于早期终止试验的可能性很高，TS设计的实际样本量小于BOP2设计的样本量。

表5 试验案例2嵌套的疗效终点中BOP2和TS设计PRN、PET及实际样本量模拟结果比较Table 5 Comparison of BOP2 and TS design PRN, PET and actual sample size simulation results in the nested efficacy endpoint of trail case 2

续表

场景θ(CR,CR+PR)PRN / %PET / %样本量BOP2TSBOP2TSBOP2TS6(0.25,0.20,0.30,0.25)(0.25,0.45)72.359.019.340.937.129.17(0.25,0.25,0.25,0.25)b(0.25,0.50)85.574.29.925.738.533.08(0.30,0.25,0.25,0.20)(0.30,0.55)95.785.23.014.839.535.9

3.3 共同主要疗效终点

表6显示了在试验案例3具有两个共同主要疗效终点(即ORR和PFS6)的模拟结果，表2列出了相应的停止边界值。场景1和7分别展示了H0和H1。将BOP2设计与Thall等[18]提出的贝叶斯设计进行了比较，并将后者简称为TSE设计。为了公平比较，TSE设计与BOP2设计使用的模型和停止规则相同，只是临界值的方式不同(TSE设计使用固定临界值C，而BOP2设计使用适应性概率阈值C(n))。结果与前述案例一致，与TSE设计相比，BOP2设计产生了更高的统计检验效能，和更低的错误终止试验的概率。

表6 试验案例3共同的主要疗效终点中BOP2和TSE设计PRN、PET及实际样本量模拟结果比较Table 6 Comparison of BOP2 and TSE design PRN, PET and actual sample size simulation results in the common primary efficacy endpoint of trial case 3

3.4 联合监测疗效和毒性终点

表7显示了在试验案例4的模拟结果，该案例同时监控疗效和毒性。场景1和7分别代表H0和H1。同样对BOP2设计与TSE设计进行了比较，TSE设计与BOP2设计使用相同的模型和停止规则，只是TSE设计在停止规则中使用了固定的临界值C。同样，在相同的Ⅰ类错误率(即场景1中的PRN)的情况下，BOP2设计的性能优于TSE设计，具有更高的检验效能，并且错误终止试验的风险较小。

表7 试验案例4联合毒性和有效性疗效终点中BOP2和TSE设计PRN、PET及实际样本量模拟结果比较Table 7 Comparison of BOP2 and TSE design PRN, PET and actual sample size simulation results in the combined toxicity and effectiveness efficacy endpoint of trial case 4

相应的停止边界在表2中列出。在这种情况下，停止边界的使用与以前的案例略有不同。例如，在治疗30位患者之后，如果CR次数≤5或毒性反应≥10，则BOP2设计将终止试验。

续表

场景θ(有效性,毒性) PRN / % PET / % 样本量BOP2TSEBOP2TSEBOP2TSE5(0.15,0.35,0.05,0.45)(0.50,0.20)41.033.851.265.330.722.46(0.15,0.40,0.05,0.40)(0.55,0.20)60.848.633.550.833.926.17(0.18,0.22,0.02,0.58)b(0.40,0.20)86.182.411.818.238.139.58(0.15,0.30,0.05,0.50)(0.45,0.20)86.483.311.113.938.339.6

4 结 论

随着Ⅰ期临床试验完成对试验药物的安全性和耐受性的初步评估，新药研发会进入Ⅱ期临床试验阶段。Ⅱ期主要目的是评估药物在推荐剂量下的治疗效果，并进一步监控药物的毒性，防止过多的患者暴露在可能无效的治疗中。其中Ⅱa期临床试验的基本特征是早期无效终止和中期go/no-go决策，只有新疗法在Ⅱ期试验阶段表现出足够强的有效性，研发才会进入到耗时更长、耗资巨大的Ⅲ期临床试验。

目前国内的Ⅰ期临床试验已不再局限于传统的3+3设计，基于区间的BOIN、Keyboard和基于模型的CRM等贝叶斯适应性设计方法也被统计专业人员、研究者所接受、掌握和应用。着眼于Ⅱa期试验高效的设计方法，本文讨论的BOP2设计是一种灵活的贝叶斯优化设计，该设计能够同时处理简单(例如二元)和复杂(例如有序，嵌套和共同多)终点。设计使用Dirichlet-多项式模型统一适应不同类型的终点。且与Simon两阶段相比，BOP2设计可以多次中期观察，在每个中期阶段，通过评估事件的后验概率来做出go/no-go决策，在原假设下，对该决策概率进行优化，以最大程度地提高检验效能或减少患者人数。模拟研究表明，较其他现存的贝叶斯Ⅱ期设计，BOP2设计精确控制Ⅰ类错误率，保证患者风险最小化，具有更高的检验效能及更低错误地终止试验的风险，弥补了贝叶斯设计和频率设计之间的差距。此外，BOP2设计可以在试验设计阶段便枚举出终止边界值。这些特性使得BOP2设计可供众多用户和监管机构使用，且易于实现。

这一高精度、对试验过程高安全保障、对患者受益最大化的方法将推动中国早期临床试验的高速发展，虽然中国的新药临床试验日渐摆脱程式化，逐渐与国际接轨，总体研发能力和监管水平有了极大水平的提高，但是，早期新药临床试验因其特殊性和复杂性，无论是方案设计、试验管理以及最后的总结分析，仍然有非常大的提升空间，急需更多的研究人员发掘高效、高精度、高质量的方法，并应用在实践当中。