检测数据和专家知识混合驱动的小样本飞机结构件装配粗差判定

朱永国，邓 斌 ，霍正书，马国祥

(1.南昌航空大学 航空制造工程学院，江西 南昌 330063；2.中航飞机汉中飞机分公司 部件厂，陕西 汉中 723213)

0 引言

传统的飞机装配质量是利用检验卡板等专用工装实施的，随着数字化测量设备在飞机辅助装配与质量检测方面的逐步应用，飞机装配协调及其检测方法正向数字化方向发展，并在国内外多个飞机型号中得到成功应用[1]。飞机结构件中薄壁件变形与回弹；以及复合材料内应力使得飞机装配偏差呈现出不确定度大、强耦合等特点，不能建立精确的装配偏差分析模型[2-5]。激光跟踪仪等数字化测量设备已在零件制造、自动装配、装配质量控制等多个飞机制造领域得到广泛应用[6-8]，充分挖掘这些数字化测量设备测得数据所蕴含的信息，为保证飞机产品装配质量提供了新的有效途径[9-10]。检测数据计算分析的首要任务是识别出装配粗差数据，并将其剔除，以保证测量信息真实可靠。经典的测量数据粗差识别基于统计判别法等数理统计方法，明显不适用于飞机小批量研制。

目前，经典粗差识别方法主要基于统计判别法，利用数理统计方法对数据进行粗差识别[11]。数据探测法、抗差估计法、随机抽样一致性法、格拉布斯准则等的粗差检测方法多数应用于控制点的粗差检测。数据探测法利用观测值函数的统计量对粗差进行探测，但是真实误差存在不确定性，可能导致误检或漏检的情况[12]。经典的抗差估计法通常依据统计量的临界值进行粗差识别，但是临界值一般根据经验进行设定，导致抗差估计法在抗差性和合理性上存在风险[13]。随机抽样一致性算法利用观测数据迭代预估最优模型参数，迭代次数多、时间长，适用于低维数据检测[14]。格拉布斯准则通过统计量与临界值的比值大小判别粗差，适用于小样本数据检测，但临界值的选择存在主观性[15]。BRETAS等[16]提出一种加权最小二乘状态估计的多测量粗差检测方法，解决了三相配电系统的粗差判定，但飞机结构件装配易受外界因素影响，易导致识别精度不高。粗差的存在会对飞机结构件装配造成较大的影响，而传统的粗差判定方法依旧存在操作繁琐、应用数据类型有限等缺陷。聚类分析法可以量化个体或对象之间的关联程度，且对样本数量没有要求，适用于小样本数据分析处理[17-20]。为此，本文引入系统聚类方法来量化装配偏差检测数据之间的差异度。虽然系统聚类法可以判断出各装配偏差测量数据的差异性，但仍存在以下两方面待完善：①飞机结构件装配质量波动范围大[21]，容易造成误判；②领域专家的先验知识被忽略，未被利用。仅利用系统聚类方法进行粗差识别，对数据的依赖性较强，容易出现违背客观规律的情况[22-23]。

综合以上分析，飞机结构件装配检测数据粗差识别是检测数据计算分析的首要任务，是飞机数字化研制面临的新问题。本文针对飞机等航空航天复杂结构产品装配偏差数据样本少、装配累积偏差值不确定性大等特点，以小样本飞机结构件装配为研究对象，提出检测数据和知识混合驱动的小样本飞机结构件装配粗差判定方法，适应了飞机数字化装配快速发展，可为飞机研制提供可靠数据。

1 检测数据和知识混合驱动的小样本飞机结构件装配粗差判定

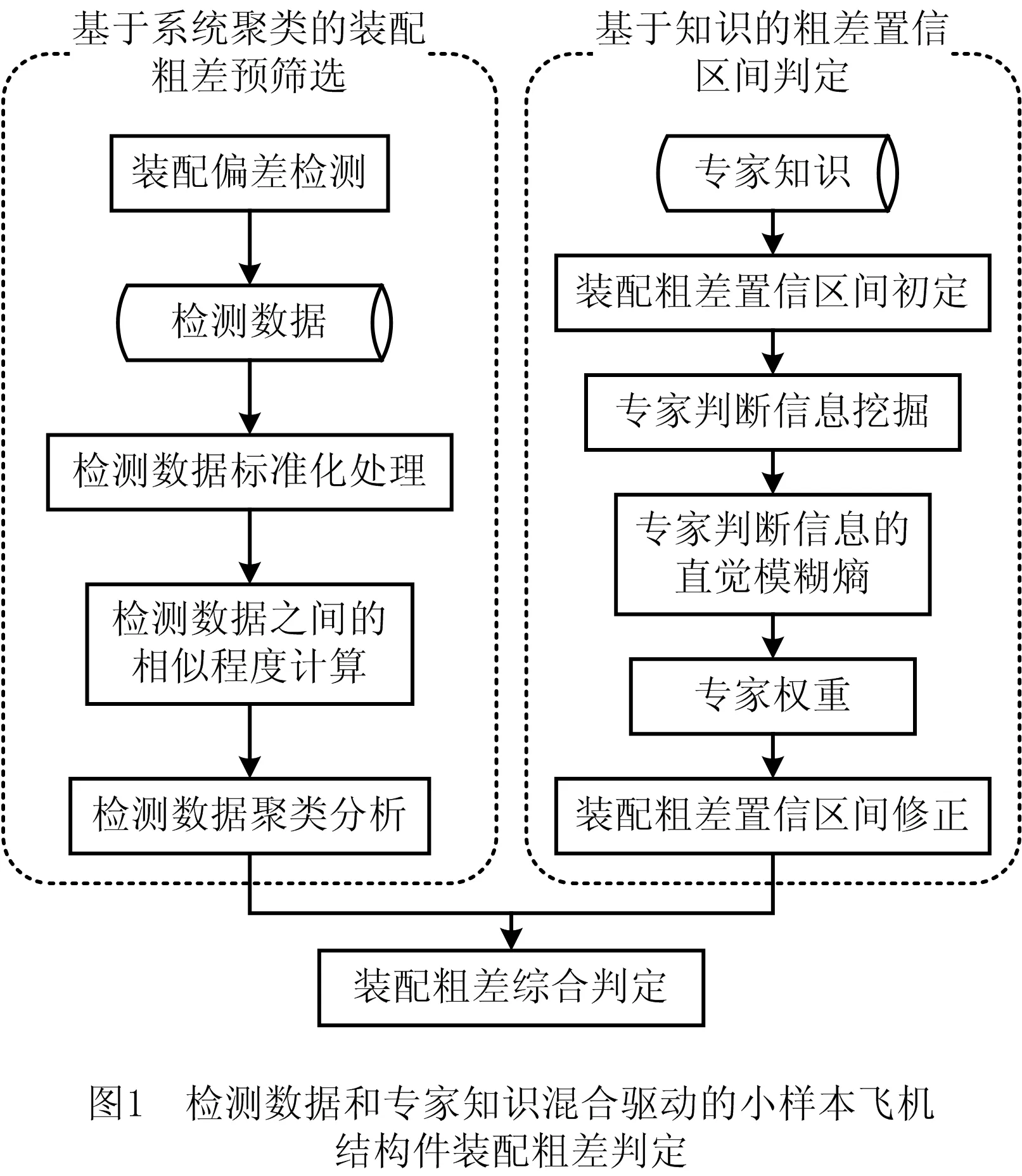
如图1所示为检测数据和知识混合驱动的小样本飞机结构件装配粗差识别流程。具体步骤如下：

(1)引入系统聚类方法，建立装配偏差测量数据聚类分析数学模型。①对装配偏差进行检测，获得装配偏差检测数据；②对装配偏差检测数据进行标准化处理；③利用欧式距离，计算装配偏差检测数据之间的相似度，对检测数据进行分类，获得相似度大的检测数据类；④运用组平均连锁量化检测数据类之间的相似度，实现检测数据类的再聚集，完成基于系统聚类装配偏差异类数据的预筛选。

(2)基于专家知识，判定装配粗差置信区间；①专家依据知识和经验初步判定装配偏差置信区间；②对专家判定装配偏差置信区间的数据进行挖掘；③引入直觉模糊熵，用精确数量化专家之间判定信息的直觉模糊相似度；④确定专家权重，对装配偏差置信区间进行修正，实现基于专家知识的粗差置信区间判定。

(3)依据系统聚类与专家知识，综合识别出存在装配粗差的结构件。

2 基于系统聚类的结构件装配粗差预筛选

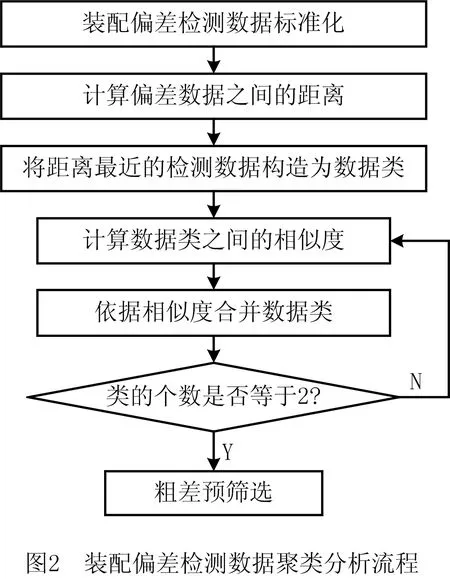
如图2所示为采用系统聚类方法实现装配粗差预筛选的流程，如图3所示为依据相似度量化评价装配偏差之间的差异程度，以实现装配偏差异常类的判定。首先，在装配质量检测数据标准化的基础上，利用欧式距离来量化装配质量检测数据之间的相似度。欧氏距离越小，表示两结构件装配质量之间的相似度越高。其次，依据欧式距离对检测数据进行聚类，构建检测数据类。然后，利用组平均连锁量化各检测数据类之间的距离。类距离越小，表示检测数据类之间的相似度越高，依据距离对检测数据类进行再聚类，实现装配粗差的预筛选。

(1)装配偏差检测数据标准化

(1)

式中:max{xδi}、min{xδi}分别表示取xδi中各元素的最大、最小值。

(2)检测数据之间相似度程度量化表示

欧式距离可表示空间中任意两点间的位置差，可实现数值特征差异的量化描述。为此，在偏差数据标准化处理的基础上，定义式(2)所示的欧氏距离来量化不同装配架次之间装配偏差的相似性。欧式距离越小，不同装配架次装配精度差异性越小，其相似度也就越高。

(2)

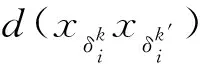
(3)检测数据类之间的相似度量化描述

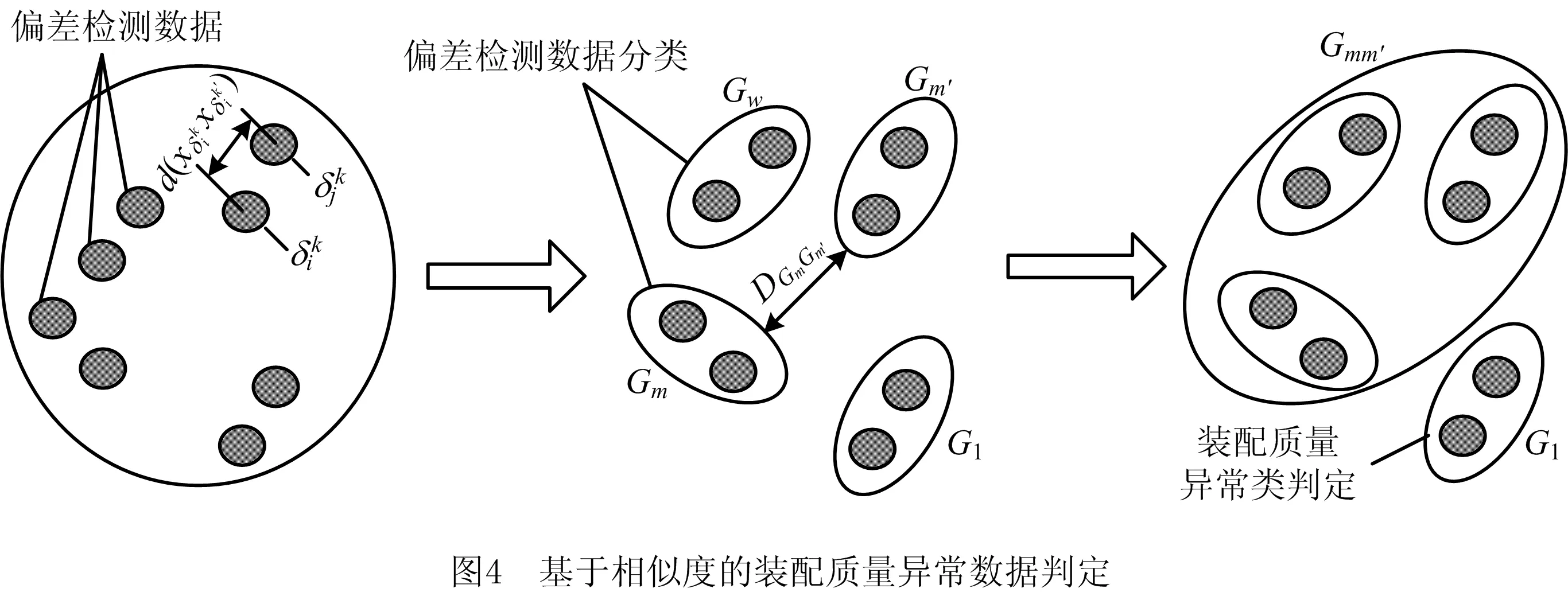
引入组平均连锁计算检测数据类之间的距离DGmGm′，以量化如图4所示检测数据类之间的相似度

(3)

式中φ1、φ2分别为检测数据类Gm、检测数据类Gm′中元素的个数。DGmGm′越小，类Gm和类Gm′的相似度越高。对相似度高的检测数据类进行聚类，如此往复，直到所有数据被分为两类为止。

3 基于加权直觉模糊熵的装配偏差置信区间判定

如图5所示为基于加权直觉模糊熵的装配偏差置信区间判定。首先，作为评价主体，专家以领域知识和经验为基础对装配偏差置信区间进行自觉判定。然后，针对专家知识信息进行挖掘，引入基于不确定性理论的直觉模糊熵法，用精确数量化专家之间判定信息的直觉模糊相似度。直觉模糊相似度越大，该专家提供的判定信息越能代表专家群体的意见，应赋予较大的权重；反之，则应赋予较小的权重。最后，根据专家权重对置信区间进行加权，得到装配偏差置信区间修正值。

(1)基于直觉模糊熵的专家权重量化

专家权重确定的方法是依据专家对于专家群体装配偏差判定区间的一致性程度来为专家赋权。首先，各专家依据各自的知识和经验给定各装配偏差分量的初始置信区间。然后，引入基于不确定度理论的直觉模糊熵法，利用直觉模糊集来表示专家给出的判定区间，计算专家判定直觉模糊数，通过将直觉模糊数转化为精确数来计算专家之间判定信息的直觉模糊相似度，最后，利用平均直觉模糊相似度确定专家权重。

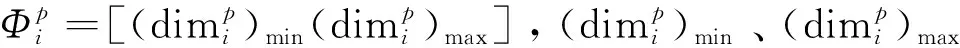
(4)

(5)

利用直觉模糊数量化任意两专家ep和eq判定信息之间的直觉模糊相似度

(6)

(7)

其中λ1、λ2分别表示专家之间直觉模糊数隶属度之间的相似程度和非隶属度之间的相似程度。

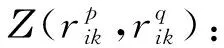
(8)

(9)

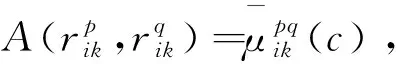
利用式(9)将相似度矩阵Zpq转化为精确数矩阵Apq：

平均相似度能够简明、直观地描述各专家之间区间判定的集中趋势。

(10)

对式(10)进行扩展，定义专家ep关于所有偏差分量的平均相似数矩阵AP:

(11)

对ωip进行扩展，可得各专家关于结构件装配偏差δ判定的权重矩阵Ω：

(2)基于专家权重的装配偏差置信区间修正

利用权重矩阵Ω，对判定区间矩阵Φ进行加权修正，即可得到装配偏差修正置信区间矩阵Φ′：

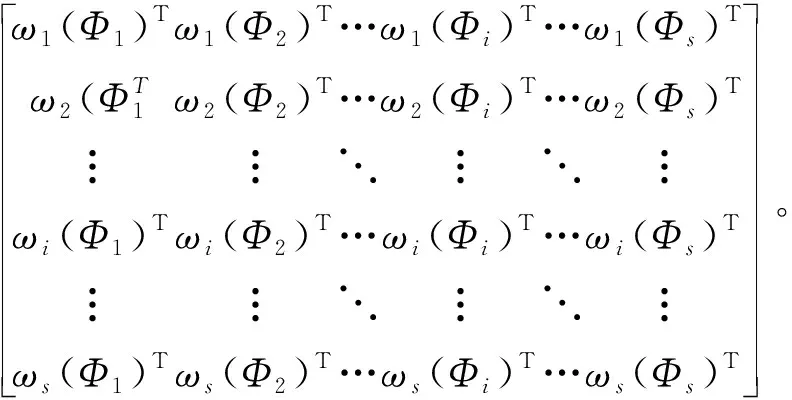
(12)

利用式(12)可求得第i个偏差分量的修正后置信区间(Φi)′：

(13)

4 应用案例

为验证检测数据和专家知识混合驱动的飞机结构件装配粗差判定方法的正确性与可行性，以某型飞机右上壁板装配为研究对象，实验中通过显著增大铆接力致使装配过程中产生异常变形，形成粗差源，导致装配粗差。该型号飞机前机身右上壁板由表1所示的变曲率蒙皮、隔框和长桁组成，零件尺寸分别如图6～图8所示，图9所示为该壁板的总体结构。该壁板各零件之间的连接方式为铆接。

本文对黑城的三件元代蒙古文、汉文文书做了释读，文书涉及亦集乃路的经济和税收，如蒙古人中的人力雇佣、亦集乃路的税粮征收，有的内容则与元朝后期亦集乃路儒学教官的赴任有关。这些文书的文字虽然有限，但在相关问题的研究方面，仍为我们提供了一些新的资料。

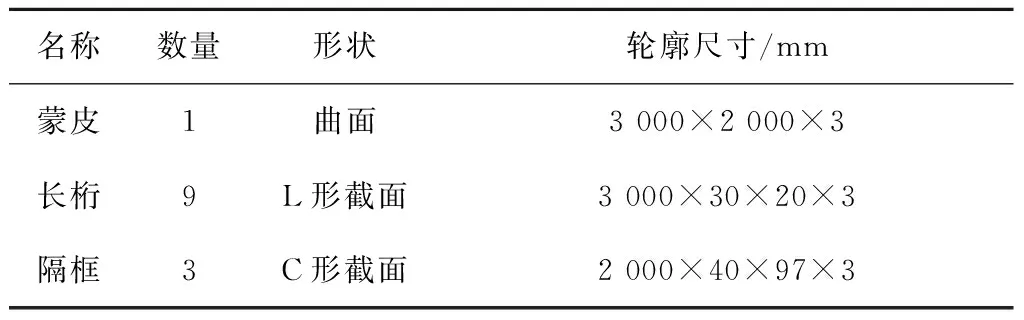
表1 某型飞机前机身右上壁板零件

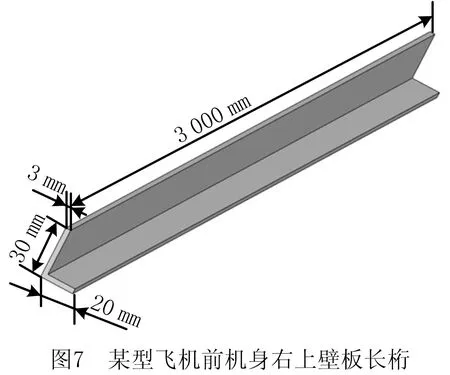
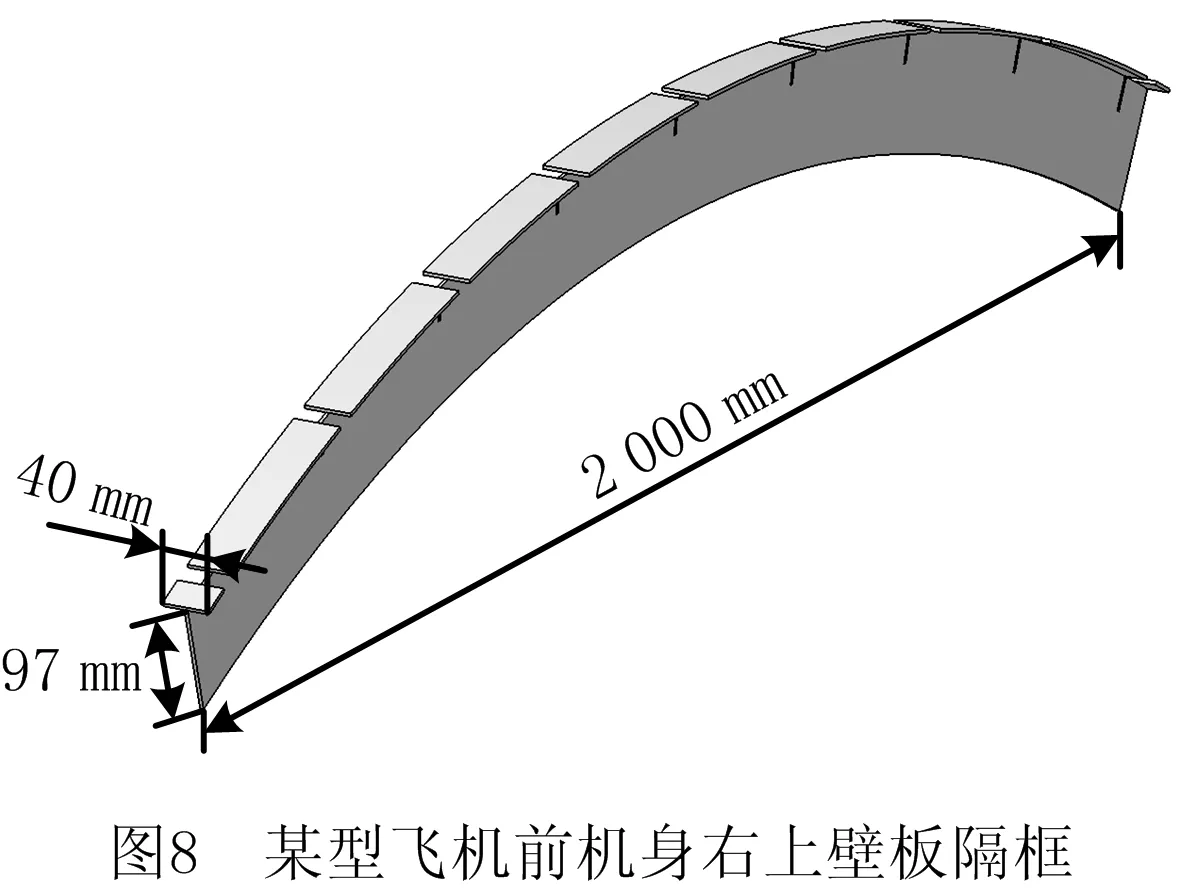
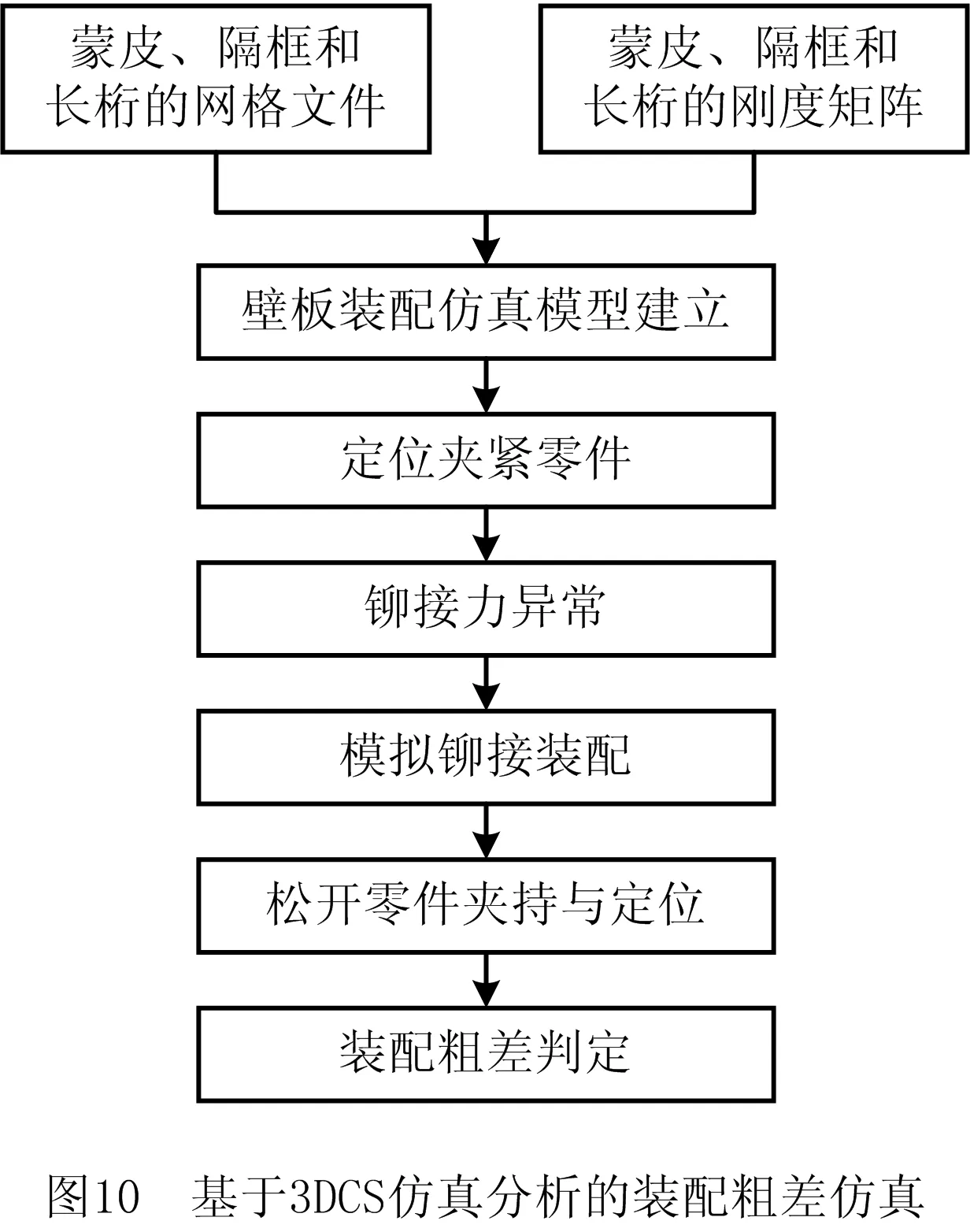
4.1 基于3DCS的装配粗差仿真分析

如图10所示为利用3DCS软件进行右上壁板装配粗差仿真流程。首先，将蒙皮、隔框和长桁的网格文件和缩减刚度矩阵分别加载到仿真模型中，作为计算变形的依据。然后，将蒙皮、隔框、长桁等模拟件定位夹紧到夹具上，并进行铆接仿真。其次，松开各个零件的夹持和定位，此时壁板装配件将发生弹性回弹。共进行10架次装配偏差仿真，其中第3、第8次装配过程中，显著增大铆接力导致装配粗差，直接影响装配质量控制点的位置度。网格文件单元类型均设置为C3D10；蒙皮、隔框和长桁的材料属性均相同，其中杨氏模量为2×1011Pa，泊松比为0.266，密度为7 860 kg/m3，延展性为1.17×10-5。

工程实际中，控制点坐标偏差是判断飞机装配后外形偏差、部件间相对位置准确度等的重要指标[24]。如飞机总装后，采用水平测量点偏差来表示飞机主要几何参数的误差。壁板的装配质量不仅包括各点的坐标偏差，还包括外形波纹度、表面平滑度等指标。为此，采用蒙皮外形关键控制点形变量，即关键控制点形变后的位置与初始位置之间的距离，来表征该壁板的装配质量。依据右上壁板装配质量关键控制点的设计要求，关键控制点分布在蒙皮中线以及外侧径向边缘起点、1/3、2/3处和终点，共有12个关键控制点，图11所示为通过关键控制点Kp1～Kp12来表征壁板的装配质量。经仿真得到表2所示各关键控制点位置度偏差。

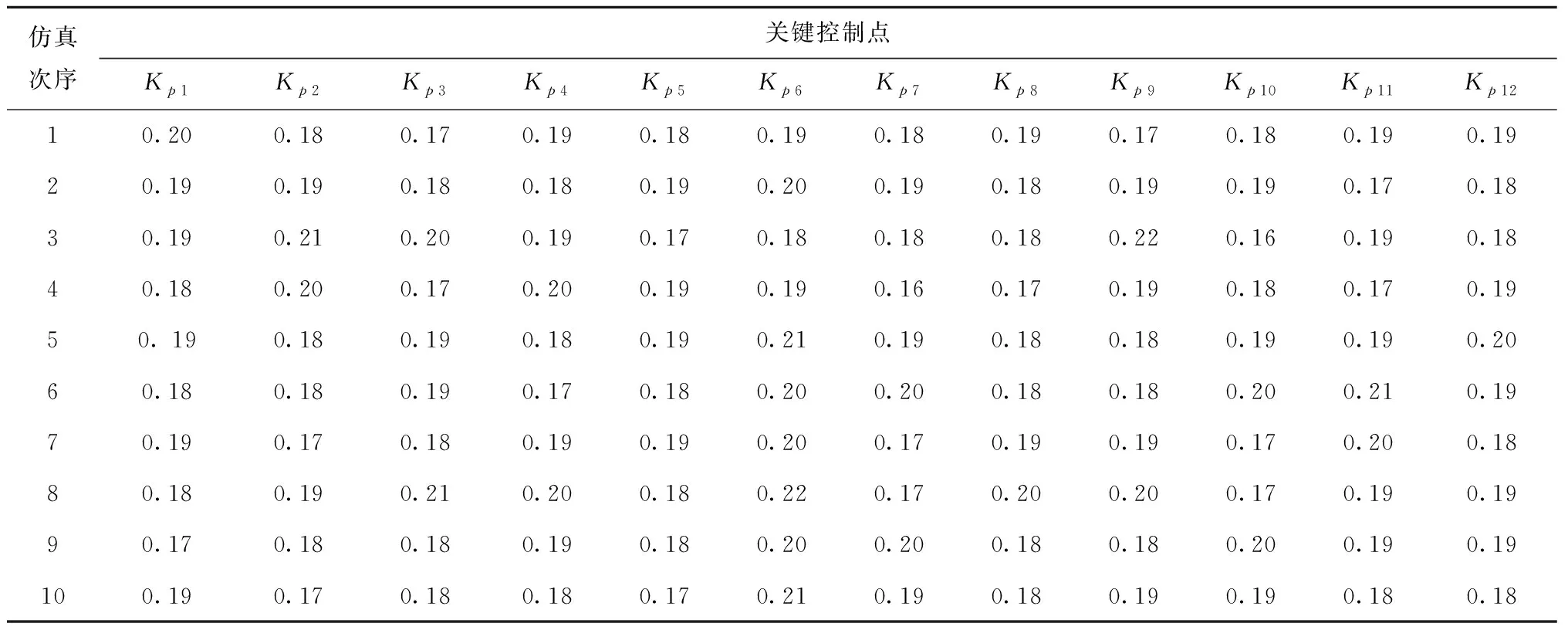
表2 关键控制点偏差 mm

4.2 检测数据和专家知识混合驱动的装配粗差判定

(1)基于系统聚类的装配粗差预筛选

依据右上壁板各关键控制点的检测数据，构建控制点偏差矩阵Dc：

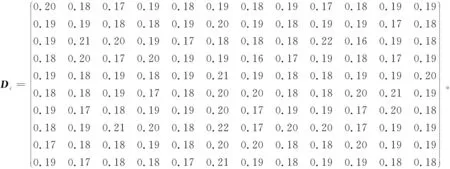
利用式(1)对Dc进行标准化处理，得

对(Dc)′进行分组，分别为G1=(Dc1)′，G2=(Dc2)′，…，G10=(Dc10)′。

利用式(2)计算G1～G10之间的欧式距离，如表3所示。

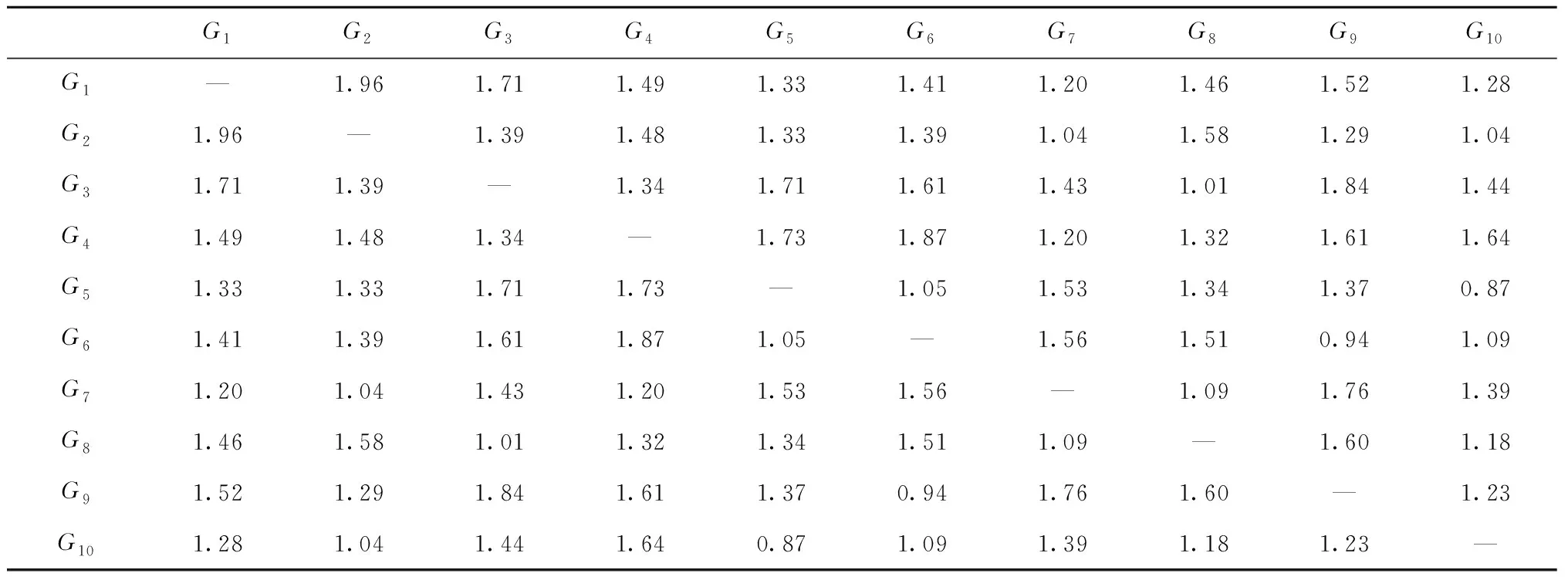
表3 G1～G10之间的距离

由表3可知，G5和G10两组数据之间距离最小，故两者之间的相似程度最大，因此，应将G5和G10聚为一类，记为G510。其余各组也依据距离大小一一进行聚类，其聚类结果分别为：G1和G7聚为一类，记为G17；G2和G4聚为一类，记为G24；G3和G8聚为一类，记为G38；G6和G9聚为一类，记为G69。

利用式(3)运用组平均连锁量化类G17、G24、G38、G510、G69之间的距离，如表4所示。

表4 G17、G24、G38、G510、G69之间的距离

由表4可知，G69和G510两类之间距离最小，将G69和G510聚为新的一类，记为G56910。G24和G17两类数据之间的距离为1.40，将G24和G79聚为新的一类，记为G2479。G38单独成一类。

利用式(3)，再次计算G56910、G1249、G38之间的距离，如表5所示。

表5 G56910、G1249、G38之间的距离

由表5可知，G56910和G1249两类之间距离最小，将G56910和G1249聚为新的一类，记为G124567910，G38单独成一类。由聚类分析结果可知，G38与其他类存在较大的差异，初步判定G38类中可能含有粗

表6 关键控制点装配偏差置信区间 mm

差，即第3次仿真或者第8次仿真可能含有粗差。

(2)专家权重求解与置信区间修正

基于表2，引入3位专家依据其领域知识和经验给出各关键控制点装配偏差的置信区间，如表6所示。

针对各次仿真实验，各专家对关键控制点Kp1～Kp12装配偏差一一进行估计，如表7～表9所示。

利用式(5)和表7～表9，经计算得各专家判定直觉模糊数，如表10～表12所示。

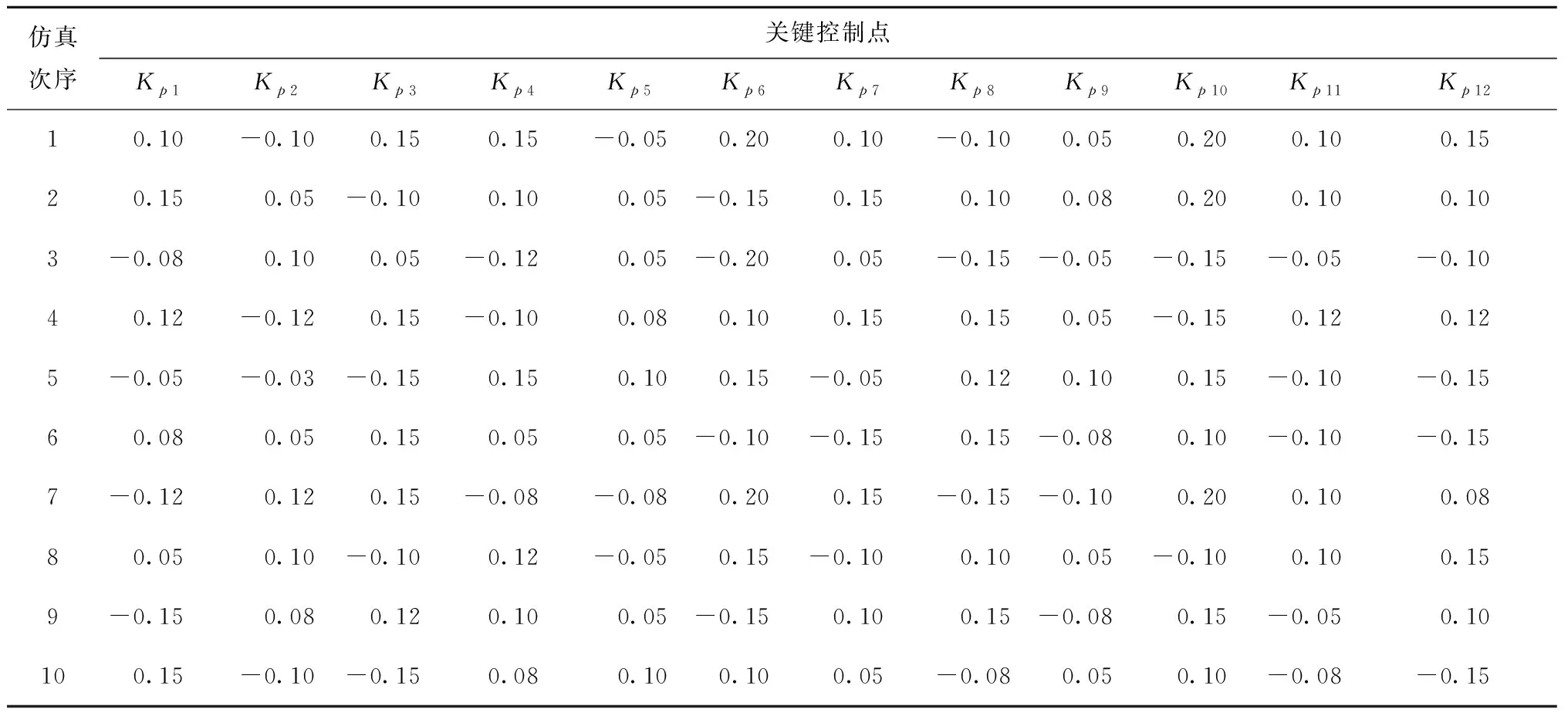
表7 专家1偏差估计值 mm

表8 专家2偏差估计值 mm

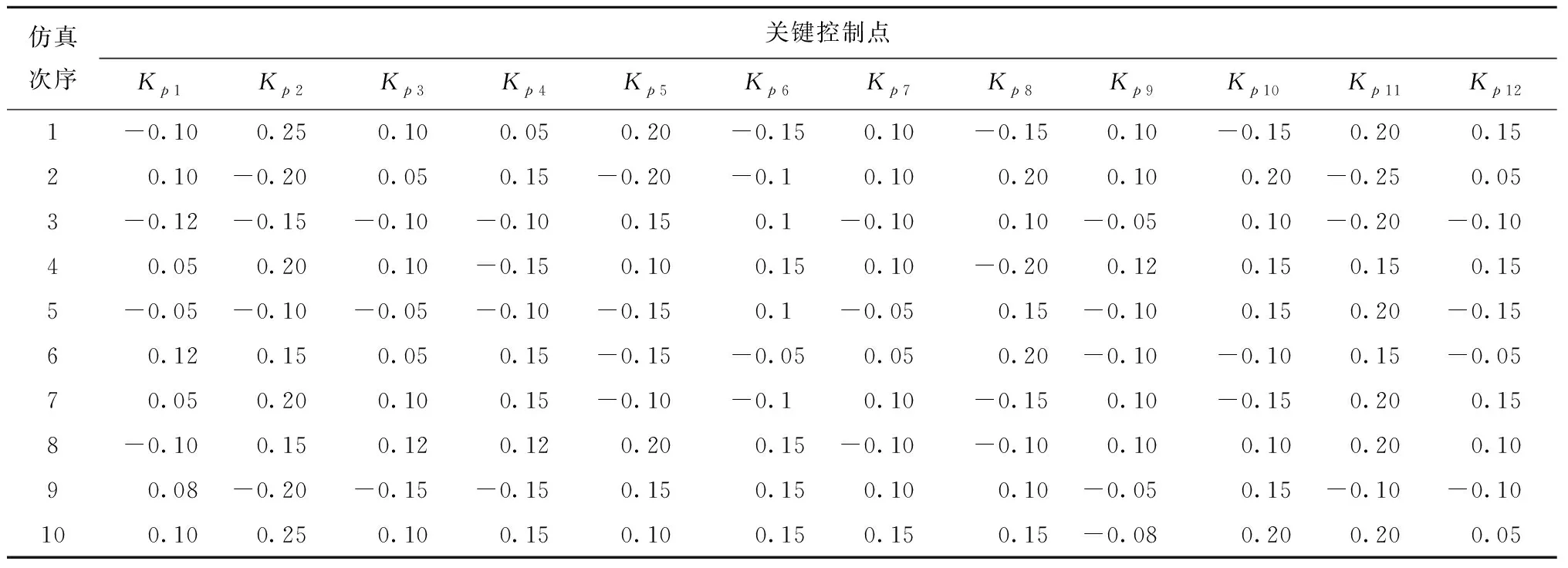
表9 专家3偏差估计值 mm

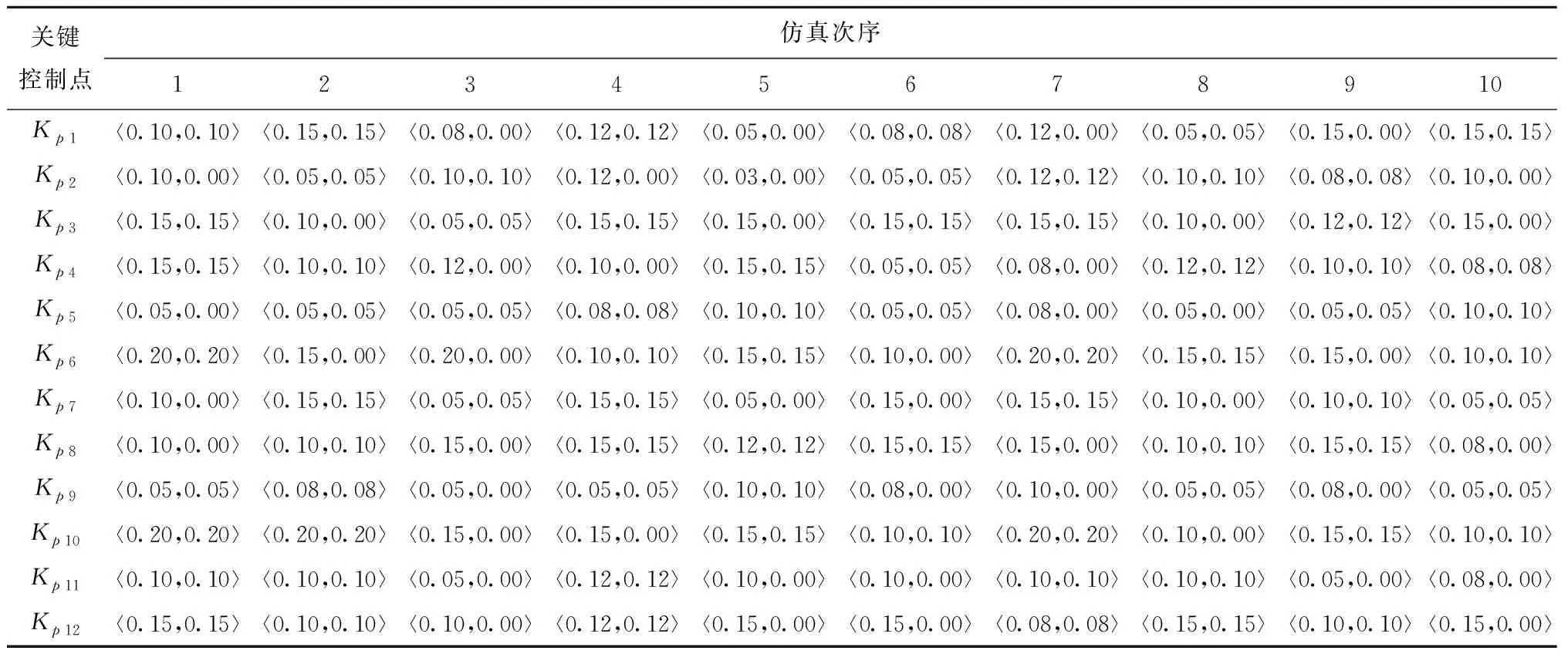
表10 专家1直觉模糊数

表11 专家2直觉模糊数

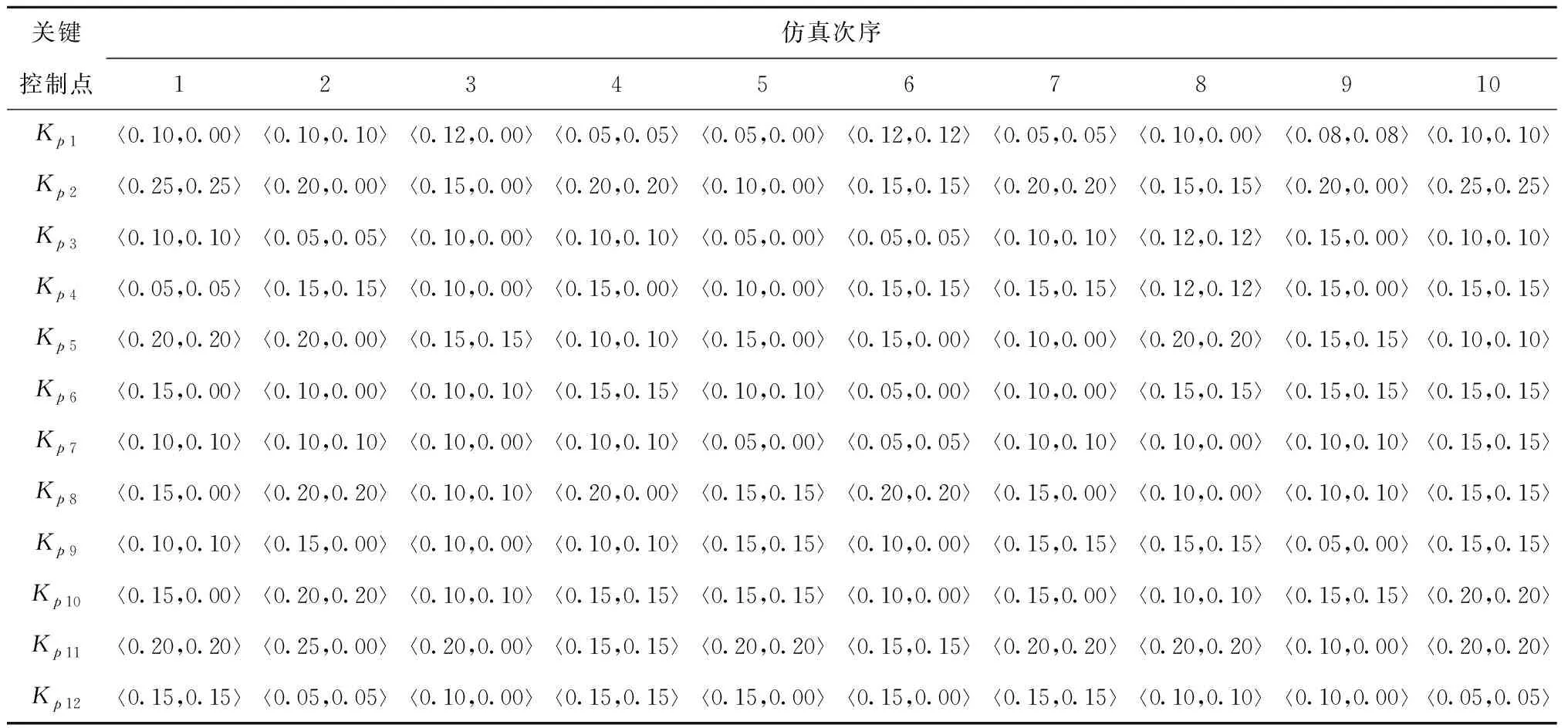
表12 专家3直觉模糊数

综合利用式(9)、式(10)和表10～表12，经计算得各专家平均相似度矩阵。

A1=[0.61 0.53 0.63 0.70 0.49 0.58 0.670 .74 0.63 0.65 0.60 0.72]，

A2=[0.53 0.54 0.72 0.70 0.62 0.54 0.65 0.69 0.65 0.47 0.68 0.62]，

A3=[0.56 0.47 0.68 0.62 0.63 0.63 0.68 0.67 0.73 0.65 0.59 0.67]。

利用式(11)和A1、A2、A3，经计算得各专家关于关键控制点Kp1～Kp12偏差判定的权重Ω

利用式(13)对初始置信区间进行修正，得到修正后Kp1～Kp12偏差置信区间分别为[-0.23, 0.23]，[-0.21, 0.21]，[-0.17, 0.17]，[-0.21, 0.21]，[-0.23, 0.23]，[-0.19, 0.19], [-0.18, 0.18]，[-0.22, 0.22]，[-0.21, 0.21]，[-0.19, 0.19]，[-0.21, 0.21]，[-0.11, 0.11]。

(3)基于聚类分析和专家知识的装配粗差识别

比较加权修正后Kp1～Kp12偏差置信区间和聚类分析异常类G38中的Kp1～Kp12偏差值，可发现：① 第3次实验Kp3、Kp9偏差值不包含置信区间中;② 第8次实验中Kp3偏差值均不包含置信区间中。综合聚类分析结果和装配偏差置信区间，可判定出第3和第8次实验都存在粗差。

4.3 实验方法分析对比

经典的格拉布斯粗差判定准则多数应用于航空航天、海洋资源勘察等领域的数据分析，取得了较好的效果[14]。利用格拉布斯准则，对飞机结构件装配粗差进行判定。其判定过程如下：

(1)排序 对表2各关键控制点位置度偏差进行从小到大排序。

(3)获取统计量 综合利用平均值、标准差，获取格拉布斯准则统计量。

(4)粗差判定 通过查询格拉布斯准则临界值检验表可知G90(10)=2.036，并与统计量进行比较。由于第3次实验中Kp9与第8次实验中Kp8位置度偏差值的统计量均大于格拉布斯准则临界值2.036，该关键控制点位置度偏差判定为粗差。

对比两者粗差判定方法结果可知：两种方法均能诊断出实验中关键控制点位置度存在粗差，但格拉布斯准则识别结果较为粗糙，存在错判和漏判的情况，如：第8次实验中的Kp8偏差值的错判、第3次实验中的Kp3偏差值的漏判等。其主要原因是经典的格拉布斯准则是依据统计量与临界值进行比较，从而判定粗差，但临界值的选择与检出水平有关，存在较大的主观性；而本文将检测数据和专家知识进行有机融合，利用平均直觉模糊相似度进行专家权重赋值，能较好地减少判定区间的主观性，并可较好地适用于薄壁件变形回弹、铆接干涉、多层级装配等多因素影响导致装配偏差不确定度大的粗差识别。

5 结束语

针对小样本、装配偏差不确定度大的飞机结构件装配检测数据预处理，本文引入测量信息论中的聚类分析法和基于不确定性理论的直觉模糊熵法，提出检测数据和专家知识混合驱动的飞机结构件装配粗差判定方法。

案例分析结果表明，与本文提出的装配粗差识别方法相比，经典的格拉布斯粗差判定准则存在漏判、错判等不足。利用本文提出的装配粗差检测方法准确实现了小样本、置信区间难以确定的飞机结构件装配粗差识别，提高了数据处理的效率，粗差识别准确率提高了12.5%，保证了数据的可靠性。

本文提出的基于系统聚类和专家判断数据融合的装配粗差检测方法具有很好的通用性，适用于航空航天等小批量复杂产品结构的数据处理和数据利用中，具有显著的工程意义。本文没有顾及到检测数据的时间分布，下一步可针对检测数据的动态特性开展深入研究。