基于数字孪生的多轴数控机床轮廓误差抑制方法
张 雷 ,刘检华 ,庄存波,王 勇
(1.天津商业大学 机械工程学院,天津 300134;2.北京理工大学 机械与车辆学院,北京 100081;3.北京理工大学长三角研究院(嘉兴),浙江 嘉兴,314000)
0 引言
随着航空航天、轨道交通、能源电力等领域的高端装备朝着精密化/复杂化/轻量化方向发展,对复杂曲面的数控加工精度要求日趋严格。作为数控机床的关键执行部件,多轴进给系统联动过程中变位姿、变负载等特点导致数控机床呈现明显的时变动态特性以及轴间动态特性不匹配。与此同时,联动过程中惯性力、摩擦力、切削力等非线性干扰必定会激发数控机床的振动与变形。这些因素均是影响轮廓误差的关键所在,直接决定着数控机床加工复杂曲面零件的轮廓精度[1]。工程中,轮廓精度是评价数控机床加工精度的重要指标之一。因此,轮廓误差抑制对提高数控机床加工复杂曲面零件的精度具有十分重要的意义。
鉴于轮廓误差抑制的重要性,国内外学者从不同角度进行了大量研究。在轮廓误差离线补偿方面,一部分学者针对轨迹曲率变化[2]、NURBS曲线轨迹[3]、切削力干扰[4]等,建立了轮廓误差与部分影响因素的函数关系,在此基础上进行速度规划,减小了轮廓误差,但是也降低了运行速度。另一部分学者考虑轨迹尖角[5]、曲率变化[6]等的影响,预估得到轮廓误差,进而对指令轨迹进行修正,在保证高速的前提下有效减小了轮廓误差。此外,学者们从不同角度提出了轮廓误差预测方法[7]、轮廓误差补偿策略[8]、离线增益调整法[9]等轮廓误差离线补偿方法。然而,离线方法建立的轮廓误差函数无法反映轮廓误差与其多种影响因素(进给系统动态特性参数、运动控制参数、非线性干扰、轮廓形状参数、运动学参数等)间的动态演变关系。
在实时插补方面,学者们起初在研究插补算法时,主要考虑几何、速度、加速度、加加速度等的约束进行速度规划[10-12],轮廓误差得以减小,但是无法将其减小至特定值。当前,学者们直接以轮廓误差为约束[13-17],考虑最小速度波动限制[14-15]和驱动限制[16]进行速度规划,根据轨迹曲率对进给速度进行调整,将轮廓误差减小至特定值。上述研究为了保证实时性,通常将各轴进给系统简化为一阶[13-15]或二阶系统[16],没有考虑进给系统的时变动态特性和轴间动态特性的不匹配。除了文献[17]考虑了切削力干扰,其他研究很少考虑非线性干扰引起的轮廓误差。此外,在进行速度规划时忽略了运动控制参数变化对轮廓误差的耦合影响。
数字孪生 (Digital Twin, DT) 是指利用数字技术对物理实体的特征、行为、形成过程和性能等进行描述与建模的过程及方法,是实现数字空间和物理空间双向映射、动态交互的重要手段之一[18],是信息物理系统 (Cyber-Physical Systems,CPS) 的关键核心技术和智能制造的关键使能技术之一,受到学术界和工业界的广泛关注。在数控装备领域,一部分学者基于虚拟模型与仿真的思想,通过将机械结构、切削过程和控制系统等进行多学科联合表达,建立了数控机床的DT模型,用于设计阶段的性能仿真与分析[19-21]。另一部分学者基于数据处理与分析的思想,针对机床运行过程中的大数据建立了数控机床的DT模型,结合OPC-UA[22]、MTConnect[23]通讯协议,通过数据挖掘与分析,实现了对机床运行状态的评估与预测。基于上述两类DT建模方法,学者们提出了虚拟模型与数据模型相结合的DT建模理念,其中虚拟模型用于表征数控机床的功能原理,数据模型用于表征数控机床的性能演变,两者的完美结合使得所建立的DT模型可以真实反映物理实体的机理和性能演变过程[24-28]。然而,针对数控装备的数字孪生体建模以及信息感知与融合的研究大多偏向概念、架构或定性分析,具体理论方法和关键突破技术的研究成果较少。
分析上述研究不难发现,轮廓误差预估精度不够高,影响了插补控制精度;插补算法未能考虑运动控制参数变化对轮廓误差的耦合影响,规划速度过于保守,降低了加工效率。基于数字孪生体建模与虚实同步,完成轮廓误差的动态精准预估,结合预估结果完成轮廓误差的综合抑制。如此,既可改善轮廓精度,还可保证加工效率。然而,如何建立随数控装备物理实体动态演变的高保真数字孪生体,如何在数控装备运行过程中实现轮廓误差的在线预测,都亟需从定量的角度进行研究[29]。
因此,本文针对数控加工中的轮廓误差抑制难题,结合数字孪生的虚实交互、同步演化等优势特点,提出基于数字孪生的轮廓误差抑制方法。首先,以多轴进给系统为具体对象,构建了面向轮廓误差的“建模-预测-控制”闭环抑制技术框架;然后,详细阐述了高保真数字孪生体建模、虚实精确同步、轮廓误差高置信动态预估以及轮廓误差综合抑制等关键实现技术;最后,以小型三轴数控机床为例,验证了所提方法的有效性。所提方法和技术对数字孪生在轮廓误差抑制领域的应用具有重要的借鉴意义。
1 面向轮廓误差的“建模-预测-控制”闭环抑制技术框架
多轴进给系统作为数控机床的关键执行部件,其运行过程中的轮廓误差直接决定着数控机床加工复杂曲面的轮廓精度。因此,以多轴进给系统为具体对象,构建轮廓误差的“建模-预测-控制”闭环抑制技术框架,如图1所示。该技术框架包括物理实体、数字孪生体、高置信动态预估模型、轮廓误差综合抑制方法、多粒度信息5部分,涉及高保真数字孪生体建模、虚实精确同步、轮廓误差高置信动态预估以及轮廓误差综合抑制4项关键技术。
物理空间中的多轴进给系统作为物理实体,具有时变动态特性、轴间动态特性不匹配、多属性交叉耦合等特点,其运行过程中还存在反向间隙、摩擦力、惯性力、切削力等非线性干扰。因此,考虑多轴进给系统时变动态特性和轴间动态特性不匹配,建立其时变耦合机理模型。针对多轴进给系统联动过程中反向间隙、摩擦力的跃变性以及惯性力、切削力的不确定性,建立多轴进给系统的数据驱动模型。将多轴进给系统的几何、物理、控制、通信等多种属性进行多领域、多维度融合,获得数字空间中能够真实映射多轴进给系统的高保真数字孪生体。
物理空间中的多轴进给系统和数字空间中的数字孪生体在运行过程中会产生海量的物理数据和孪生数据,如:振动、电流、位移、速度、应力、应变等,这些数据具有频率不同、量级不同、类型异构等特点,将其称为多粒度信息。多粒度信息的传输具有跨协议、跨接口的特点。因此,针对上述特点,建立数字-物理空间双向感知关系。针对多轴进给系统的性能状态(动态特性、跟随误差、轮廓误差等)动态演变现象,构建数据驱动的慢时间尺度数字孪生体同步演化模型,融合物理数据驱动数字孪生体的动态更新与重构。针对多轴进给系统的运行全过程,在数字空间对其性能状态进行量化表征,实现多轴进给系统运行全过程的性能状态虚实精确同步。

为了提高数字孪生体仿真预测的实时性,通过对数字孪生体进行降阶表征,建立轮廓误差与其多种影响因素(进给系统动态特性参数、运动控制参数、非线性干扰、轮廓形状参数、运动学参数等)间的动态映射模型。对数字-物理空间的多粒度信息进行跨空间深度融合,获得轮廓误差在线预估模型。对历史数据集进行更新学习与样本重训练,针对参数曲线轨迹实现轮廓误差的高置信动态预估。
将轮廓误差与其多种影响因素间的动态映射关系以及轮廓误差的动态预测结果作为轮廓误差综合抑制的基础,以轮廓误差最小化为目标,以弓高误差、向心加速度、向心加加速度等为约束,通过迭代、仿真、预测与优化,获得限制速度和运动控制参数的最优解或次优解。考虑加工时间最短,以最大限制速度、最小速度波动为限制条件,进行曲线分段和速度规划,获得平滑速度曲线,结合最优运动控制参数作为插补控制输入,实现对物理空间中多轴进给系统的反馈控制。
轮廓误差“建模-预测-控制”闭环抑制技术框架中,物理空间完成轮廓误差控制指令的输入与执行,数字空间完成与物理空间的同步以及轮廓误差动态预估,物理空间与数字空间通过多粒度信息实现实时交互与感知。由于考虑了物理空间中多轴进给系统的运行性能和运动控制参数的时变性,该技术框架的整个过程是不断循环往复的,能够实现对多轴进给系统轮廓误差的有效抑制。
2 基于数字孪生的轮廓误差抑制关键实现技术
2.1 多轴进给系统数字孪生体建模
考虑到多轴进给系统具有结构、力学、控制、通信等多属性交叉耦合的特点,数字孪生体建模需要涉及动力学、系统辨识、运动控制、信号测试、机器学习、网络通讯与计算机等多领域建模技术。与此同时,多轴进给系统运行过程中位姿、速度、加速度的变化以及非线性干扰的影响,导致其动态特性呈明显的时变性、轴间不匹配性和不确定性,数字孪生体建模需要顾及机理和数据的双重驱动。因此,本文针对多轴进给系统的上述特点,提出机理-数据混合驱动的数字孪生体多领域、多维度融合建模方法,如图2所示。
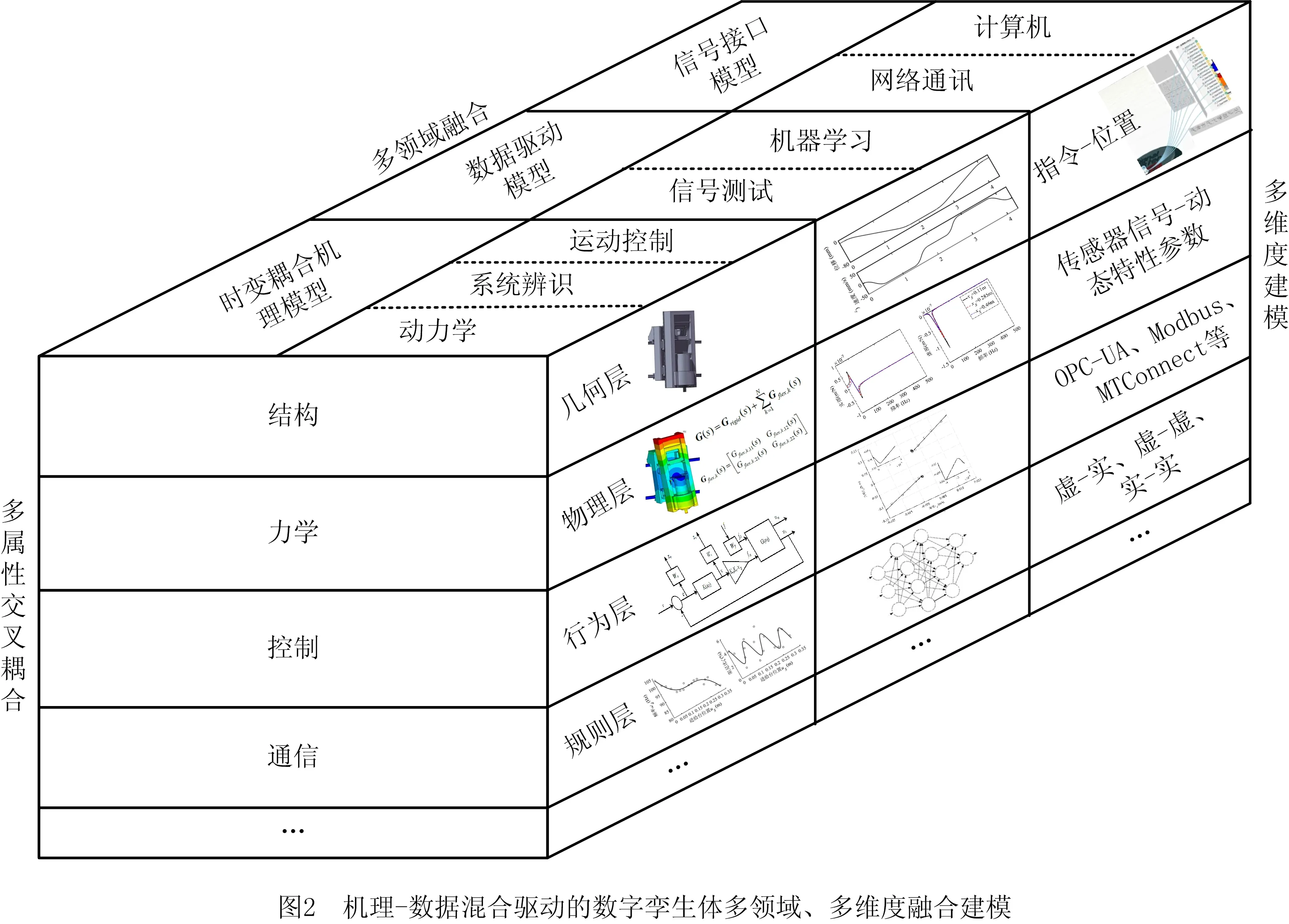
时变耦合机理模型是数字孪生体的核心基础,为保证数字孪生体的高保真度,从几何层、物理层、行为层以及规则层等多个维度对时变耦合机理模型进行建模。多轴进给系统的结构属性主要包括形位尺寸、装配关系和相对运动关系等,在几何层对其进行表达;多轴进给系统的力学属性主要包括静力学、动力学等,在物理层对其进行表达。针对多轴进给系统动态特性的时变性,考虑刚柔耦合振动与机电耦合刚度的影响,采用达朗贝尔定理与拉普拉斯变换,得到进给系统的多自由度刚柔耦合传递函数模型,统一表示为
(1)
式中:Grigid表示刚体传递函数矩阵,Gflex,k表示第k阶弹性体传递函数矩阵,s表示复变量。通过辨识实验,采用最小二乘法、正交多项式曲线拟合法等,估计得到进给系统的时变刚柔耦合传递函数矩阵,统一表示为:
(2)

多轴进给系统的控制属性用于各轴的运动与定位控制,常用的控制算法包括PID控制、滑模控制、鲁棒控制等,为了体现动态特性的时变性和轴间不匹配性,采用基于全局任务坐标系的多参数增益调度控制策略,在行为层对其进行表达,得到多轴进给系统的时变耦合机理模型,用状态空间模型统一表示:
(3)
同样地,行为层是基于物理层的时变耦合传递函数矩阵,集成增益调度控制策略的深层次表达。为了表征多轴进给系统的内在规律,需要从规则层对其进行表达,反映多轴进给系统的结构参数、动力学参数、控制器参数等的变化规律。
多轴进给系统运行过程中存在着反向间隙、摩擦力、惯性力和切削力等非线性因素,这些因素属于随机、不确定性干扰因素,当这些因素发生作用时,时变耦合机理模型将不足以准确表达多轴进给系统的内在机制和性能状态。因此,需要借助信号测试与机器学习等方法,建立多轴进给系统的数据驱动模型。同样的,从几何、物理、行为、规则等多个维度对其进行表达。
在几何层,针对进给系统反向间隙的跃变性,借助伺服驱动器,采集得到各轴的位移、速度、加速度等数据,采用机器学习方法,表征反向间隙对多轴进给系统位姿变化的影响关系。在物理层,针对惯性力、切削力的不确定性,借助伺服驱动器和外置传感器采集位置和力的数据,采用机器学习方法,表征惯性力和切削力作用下多轴进给系统的动态响应。在行为层,针对反向间隙和摩擦力的跃变性,采集位移、速度、力矩等数据,采用高斯过程回归法,表征多轴进给系统运行过程中死区、爬行等跃变现象。在规则层,通过对采集得到的多种数据进行大数据分析,采用深度学习方法,表征非线性外干扰作用下多轴进给系统位姿、动态响应、跃变及其相互间的影响关系。在数据驱动模型中,从几何层到规则层同样遵循层层深入的逻辑方式。
为了保证数字孪生体与物理实体间,以及数字孪生体各部件间的数据交互,需要建立信号接口模型。针对多轴进给系统的控制系统、伺服驱动、机械传动、传感器间的信号传递过程,在几何层着重建立指令信号与位置参数间的关系接口,在物理层着重建立传感器信号与动态特性参数间的关系接口,在行为层着重建立数字-物理空间信号传输的协议接口,在规则层着重建立虚-实之间、虚-虚之间、实-实之间的信号传递格式、译码规则等。
考虑到时变耦合机理模型、数据驱动模型和信号接口模型分别从不同学科领域对多轴进给系统进行了表达,基于通用语义表征方法,采用统一建模语言,将时变耦合机理模型、数据驱动模型、信号接口模型,从几何层、物理层、行为层、规则层等方面分别进行集成表达,得到多轴进给系统的高保真数字孪生体,以真实映射物理实体的性能状态及其内在影响因素。
2.2 多轴进给系统虚实精确同步
物理实体与数字孪生体间的数据交互是实现多轴进给系统虚实同步的前提保障。多轴进给系统的数据信息主要通过数控系统、伺服驱动器、外置传感器等进行传输,这些数据信息的采样频率、量级、类型等各不相同,故将其称为多粒度信息。此外,多粒度信息的传输具有跨协议、跨接口的特点。因此,基于总线、网口、串口传输机制,采用Modbus、OPC-UA、MTConnect、NCLink等具备强兼容性的通讯协议,建立数字孪生体与物理实体间的双向感知关系,如图3双向感知部分所示。数字孪生体通过信号接口感知物理实体的多粒度信息,将各类数据信息分别传输至时变耦合机理模型和数据驱动模型,为其提供同步更新的数据基础,进而实现数字-物理空间多粒度信息的精细化感知。
多轴进给系统的虚实同步不但需要位姿的同步,而且需要特征、性能的同步,甚至是逻辑、规律的同步,因此,基于所建数字孪生体的构成特点,分别从几何、物理、行为、规则等多个维度建立物理实体与数字孪生体间的同步机制,进而实现多轴进给系统的虚实精确同步。如图3虚实同步机制部分所示,在几何层,物理实体通过数控系统将CNC(Computer numerica control)代码等指令数据传输至指令信号接口,驱动数字孪生体完成位移、速度、加速度以及跃度的实时改变,与此同时,数字孪生体将改变后的位姿数据反馈给伺服驱动器,从而实现位姿的虚实同步。
为了准确表征物理层、行为层以及规则层的虚实同步,在标准时间t的基础上引入慢时间T,令t≤T≤3t。考虑物理实体动态特性、控制器参数、性能状态动态演变的特点,分别针对物理层、行为层和规则层的同步需求,基于所建数字孪生体提取关键表征参数,构建慢时间尺度下数字孪生体重构模型,融合物理数据驱动数字孪生体在物理层、行为层和规则层实现同物理实体慢时间尺度下的同步。
如图3虚实同步机制部分所示,在物理层,提取应力、应变、固有频率、阻尼比等作为关键参数,物理实体通过外置传感器将力、振动等时域信号和转化后的频域信号传输至时频域信号接口,在慢时间尺度下驱动数字孪生体重构以及关键参数的动态更新,从而实现静、动力学特性的虚实同步,通常取T=2t~3t。在行为层,提取控制器参数、摩擦力、爬行等作为关键参数,物理实体通过伺服驱动器将电流、转矩等传输至相应的信号接口,在慢时间尺度下驱动数字孪生体重构以及关键参数的实时更新,从而实现控制性能和跃变现象的虚实同步,通常取T=1t~2t。在规则层,提取位姿、动态特性、性能状态等作为关键参数,融合物理实体的各类实时数据、历史数据等,采用在线学习对数字孪生体重构模型进行修正,驱动关键参数的动态更新,从而实现演变规则的虚实同步,通常取T=1t~2t。

基于数字-物理空间的双向感知关系以及不同维度的虚实同步机制,从数字孪生体的几何层、物理层、行为层和规则层等多个维度,采用Apriori、C4.5、KNN(K-nearest neighbor)等机器学习算法对物理空间和数字空间的多粒度信息进行关联与分类处理,进而采用多元回归法、逐步回归法等对具体关联或同类数据进行挖掘与融合处理,得到各个维度上的有效数据。在此基础上,根据性能状态参数的理论计算公式,对多轴进给系统的动态特性(刚度、阻尼、固有频率)、跟随误差、轮廓误差等参数进行量化与赋值,最终实现数据驱动的虚实精确同步。
2.3 轮廓误差高置信动态预估
在多轴进给系统的运行过程中,对轮廓误差的影响因素众多,其中:进给系统的动态特性参数主要包括固有频率和阻尼比,统一用Dy表示;运动控制参数主要包括各类控制器参数,统一用Co表示;非线性干扰主要包括摩擦力、切削力、惯性力等,统一用Di表示;轮廓形状参数主要包括曲率、拐角等,统一用Sh表示;运动学参数主要包括速度、加速度、加加速度等,统一用Mo表示。与此同时,各影响因素相互耦合、彼此影响,如:动态特性参数直接影响着各类控制器参数,尤其是基于模型的控制器参数;非线性干扰会改变系统的动态响应;轮廓形状参数是运动学参数的重要约束,而运动学参数又会影响系统的动态响应和控制器参数。此外,多轴进给系统运行过程中,轮廓误差及其影响因素是时刻变化的,它们之间的关系是时变和动态的,而且这种关系很难用函数形式来描述。
为了准确描述轮廓误差与其影响因素间的复杂关系,并保证模型计算的高效性,采用核主成分分析(Kernel Principal Component Analysis,KPCA)、Relief算法、局部线性嵌入法(Locally Linear Embedding,LLE)等方法对数字孪生体进行降阶表征,得到轮廓误差与其多种影响因素间的动态映射模型,表示为:
CE=M(Dy,Co,Di,Sh,Mo)。
(4)
其中:CE表示轮廓误差,M表示轮廓误差与其影响因素间的映射关系,具体如图4所示。融合实测数据、软传感数据、计算数据、指令数据、机理公式等,采用Q-Learning、深度强化学习(Deep Reinforcement Learning,DRL)等强化学习算法对动态映射模型进行训练与精度修正,得到轮廓误差在线预估模型。
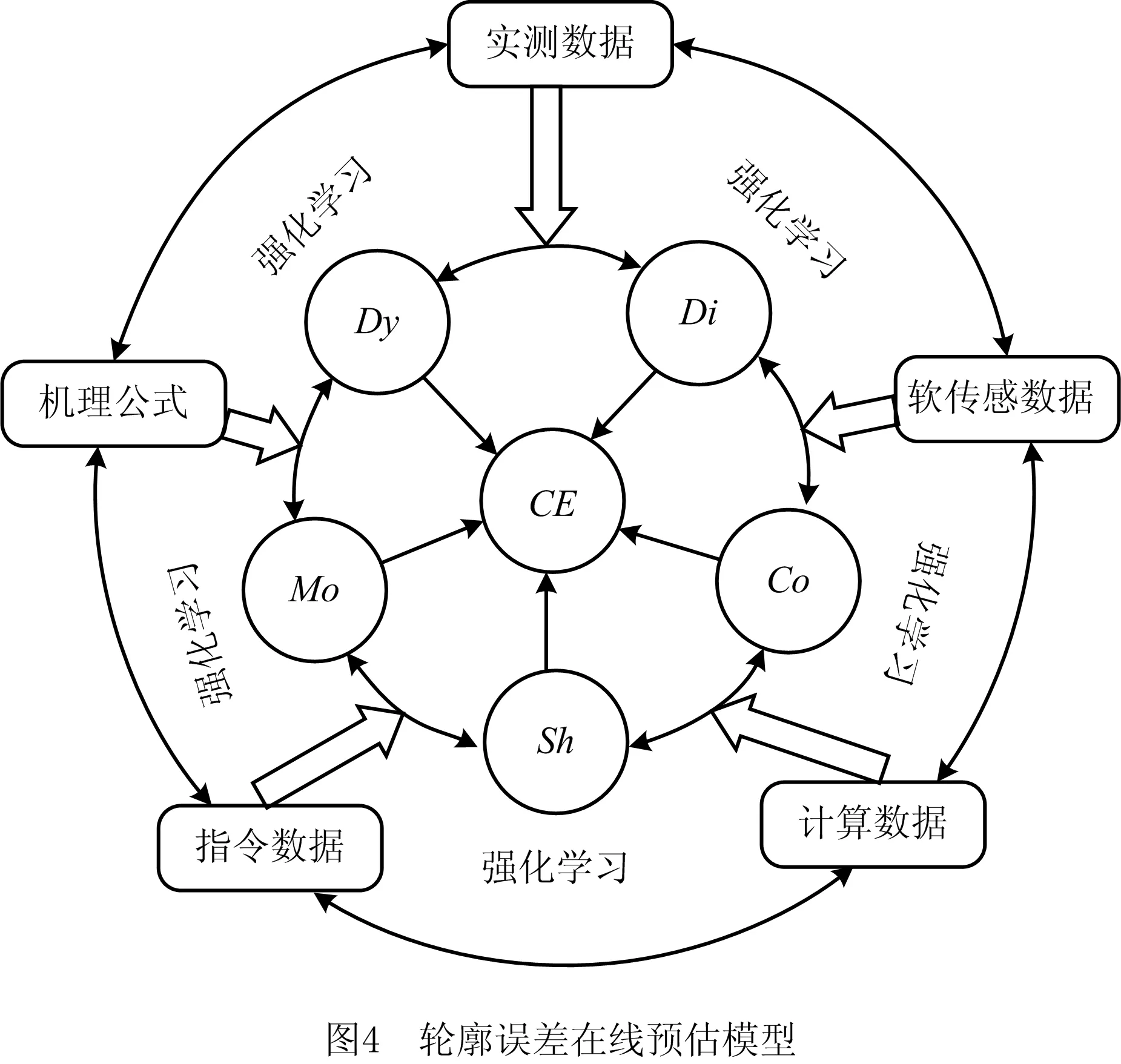
训练预估模型所用到的多粒度信息主要包括实时数据和历史数据,实时数据是轮廓误差在线预估模型能保持动态变化特性的关键所在,而预估模型的准确性更依赖于历史数据。针对实时数据量小而不足以保证模型准确性的特点,基于大量的历史数据,采用Bayes方法扩充样本数据。针对历史数据无法支撑在线预估精度的特点,基于规则对多轴进给系统运行过程中的数据集进行更新学习,对偏差较大的样本重新进行训练,保证数据的时效性,从而实现多轴进给系统轮廓误差的持续高置信预估。
2.4 轮廓误差综合抑制
作为轮廓误差抑制的主要手段之一,插补算法主要考虑几何约束、运动学约束、轮廓误差约束等对轨迹速度进行规划,通常假设运动控制参数是不变的。然而,高速运动中的多轴进给系统的动态特性是时刻发生变化的,致使运动控制参数必须是时变的,方能保证运动的高精度和平稳性。因此,重点考虑运动控制参数变化及其对轮廓误差的影响,首先采用多目标优化算法得到最优运动控制参数及与其相应的轨迹最大限制速度,然后将最大限制速度和其他常规因素作为约束,对多轴进给系统进行插补控制,从而实现时变运动控制参数下的轮廓误差抑制。
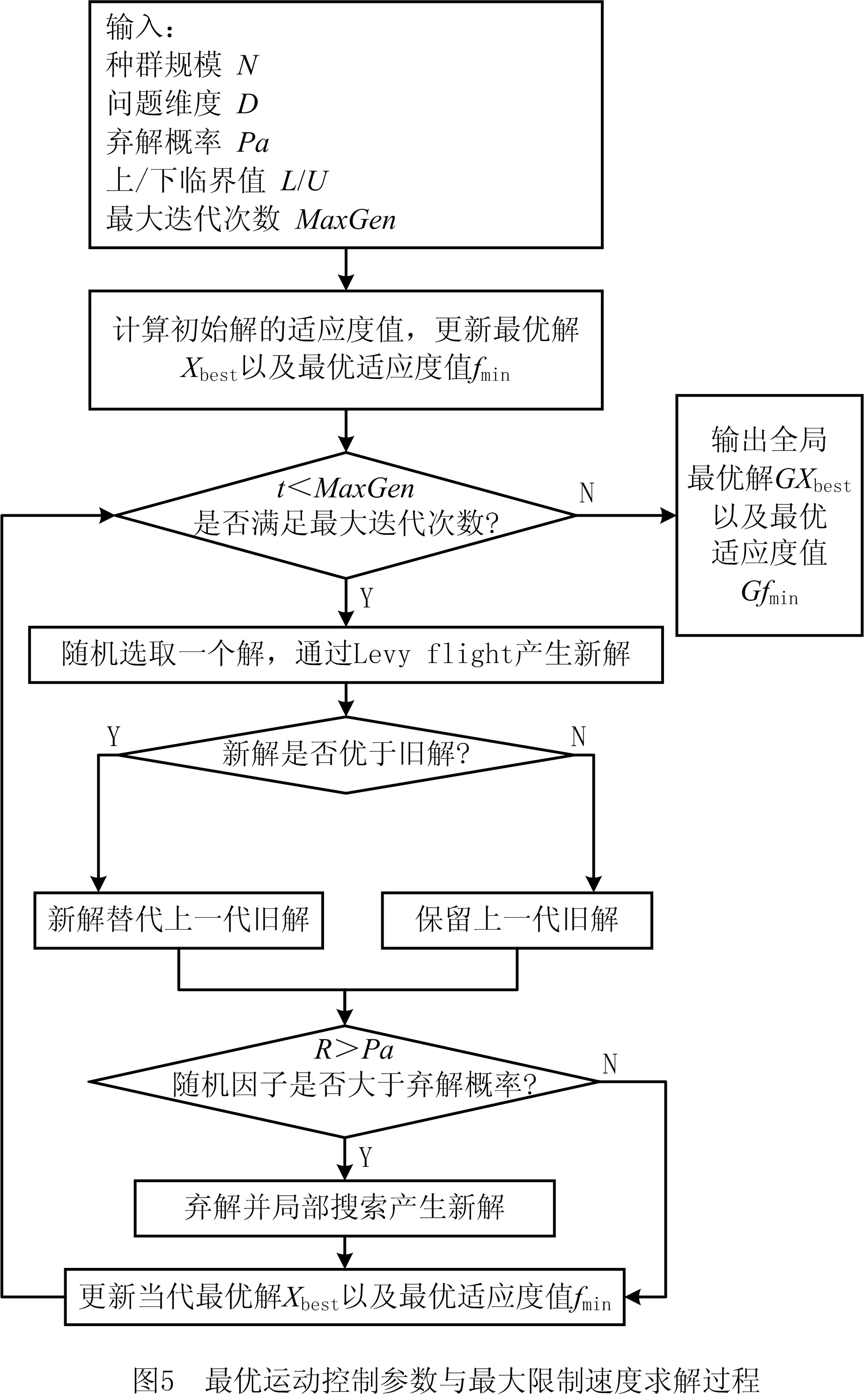
最优运动控制参数与参数曲线最大限制速度的求解流程如图5所示,基于轮廓误差与其多种影响因素间的动态映射模型,以轮廓误差最小化为目标,以弓高误差、向心加速度、向心加加速度等为约束,采用布谷鸟算法在限制速度和运动控制参数的可行域中进行寻优,其中:L/U表示最优运动控制参数与最大限制速度的上下临界值,适应度值f表示轮廓误差,解X表示最优运动控制参数与最大限制速度。
首先,根据经验和布谷鸟算法规则确定输入项,并根据轮廓误差在线预估模型计算得到初始适应度值。然后,对于迭代次数未达到最大的情况,随机选取一组解,并通过Levy flight产生新解,进而判断新解是否优于旧解,选取较优的解。通过判断弃解因子是否大于弃解概率,决定是否进行局部搜索并产生新解,并根据新解来更新最优解和最优适应度值。如此循环,直至得到全局最优解及最优适应度值,全局最优解即为包括轮廓误差在内的多约束条件下的参数曲线最大限制速度以及最优运动控制参数。
以得到的参数曲线最大限制速度为基础,采用参数曲线匀速分段算法进行曲线分段,如图6所示。将参数曲线上具有局部最大进给速度的点或断点间的区域作为关键区域,并据此将参数曲线划分为若干分段。为了避免进给速度的频繁波动,将各关键区域的最小进给速度确定为该区域的恒值进给速度,获得速度规划所需的分段曲线约束和规划参数信息,如起点或终点参数、估计长度、起点或终点参数最大进给速度等。然后,考虑加工时间最短,采用双向扫描前瞻算法进行速度规划,得到几何约束、动态性能约束以及最大限制速度、最小速度波动限制下的平滑速度曲线,如图6所示。将参数曲线对应的平滑速度规划与最优运动控制参数作为插补控制输入,实现多轴进给系统轮廓误差的综合抑制。

3 应用验证
以某小型三轴数控机床为例,验证本文提出的基于数字孪生的轮廓误差抑制方法。该小型三轴数控机床的物理实体如图7a所示,主要由数控系统、伺服驱动单元和机械结构组成。其中,伺服驱动器安装在机床床身内部,未在图中显示。机械结构部分主要包括X/Y/Z三个方向的进给系统,各轴进给系统均由伺服电机和滚珠丝杠副构成。按照本文提出的数字孪生体建模方法,建立小型三轴数控机床的数字孪生体,并借助智能制造系统可适应规划仿真平台软件(VE2)对其进行可视化呈现,如图7b所示。其中,数控系统采用C/C++编程语言,插补算法采用匀速分段算法和双向扫描前瞻算法,轮廓误差控制采用交叉耦合控制算法。各轴伺服系统采用PID控制,各轴进给系统的机械结构均通过传递函数建模与系统辨识建立时变耦合模型,与PID控制器一起形成各轴进给系统的伺服控制回路,并借助Python语言将上述模型集成于VE2软件中。借助VE2软件为各轴进给系统建立信号通讯接口,采用Modbus通讯协议实现物理实体与数字孪生体间的数据传输与双向交互,并通过C#语言对状态参数进行量化与可视化表征,进而实现数字—物理空间的虚实同步。


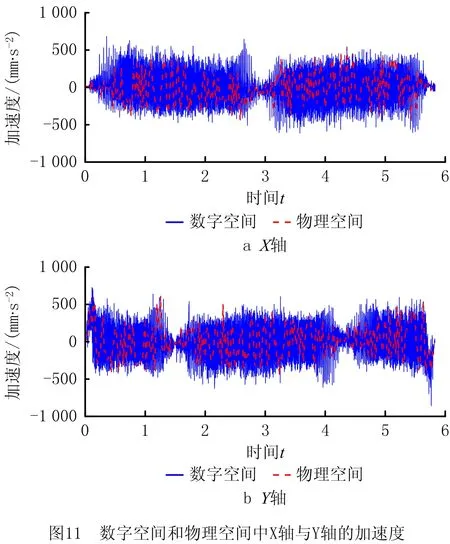
以半径为30 mm的整圆轨迹为例进行虚实同步运动实验,实验装置如图8所示,通过网口通讯的方式将物理空间中的数控系统与VE2软件中的数字孪生体建立通讯关系,通讯时间间隔为20 ms。在VE2软件中输入运动指令,其中轨迹进给速度为2 000 mm/min,切向加速度为500 mm/s2。数字空间中各轴的运动数据借助VE2软件的统计功能进行可视化呈现与存储,物理空间中各轴的运动数据通过伺服电机编码器得到。为了避免实验结果存在偶然性,该实验重复了3次,其中第3次虚实同步运动过程中,数字空间和物理空间的X/Y轴的位移、速度和加速度分别如图9、图10和图11所示。
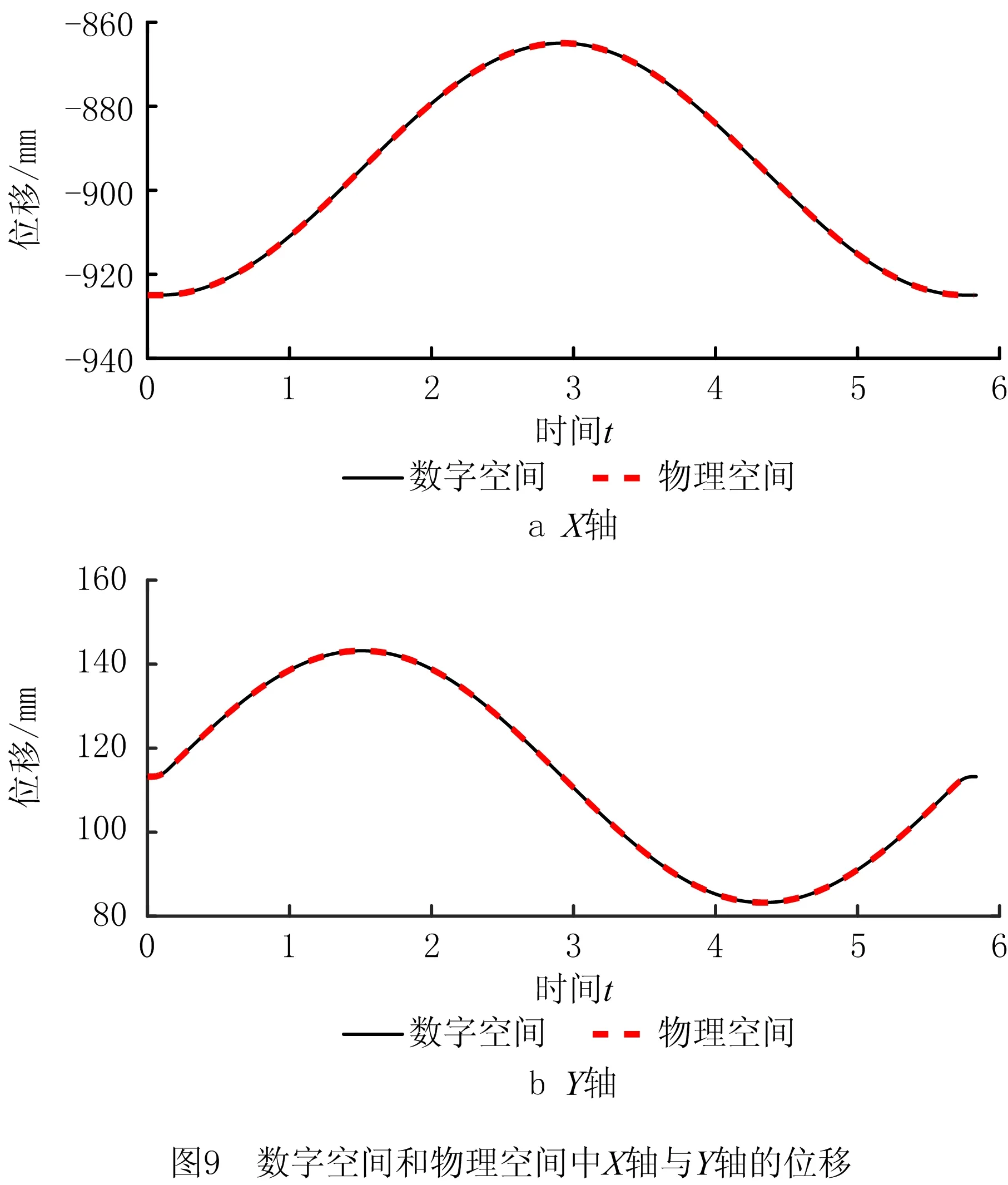

由图9可知,在数控机床按照整圆轨迹运动的过程中,数字空间和物理空间下X轴与Y轴的位移均能保持同步。由图10可知,数字空间和物理空间下X轴与Y轴的速度从趋势上可以保持同步,但是不能完全保证每个插补周期都能保持同步,究其原因,相对于插补周期而言,数字—物理空间的通讯周期较长,难以将数字空间中的实时插补数据传输至物理空间。同样的原因导致数字空间和物理空间下X轴与Y轴的加速度也仅能从趋势上保持同步,具体如图11所示。
3次虚实同步运动实验得到的整圆运动轨迹轮廓误差如表1所示,其中第2次虚实同步运动实验的轮廓误差如图12所示。

表1 整圆运动轨迹的轮廓误差 μm
由表1可知,第2次实验的轮廓误差最大,数字空间和物理空间中的轮廓误差最大值分别为19.3 μm和19.2 μm,但是跟其他两次实验结果相比,轮廓误差的最大值相差无几。此外,3次实验的轮廓误差平均值均为14.7 μm,均方根值均为15 μm,因此3次实验的轮廓误差基本相同。
由图12可以看出,虚实同步运动过程中,数字空间和物理空间下的轮廓误差值可以大致保持一致,但是无法实现在每个插补周期内保持一致,进而导致数字空间和物理空间下的轮廓误差最大值不相等,其根本原因同样是数字—物理空间的通讯周期大于插补周期。虽然数字空间和物理空间下各轴运动不能实现插补周期内的同步,但是对整圆运动过程而言,数字空间和物理空间中的轮廓误差均值和均方根值都相等。综上所述,物理空间中X轴和Y轴在执行数字空间反馈的控制指令时,能够保证一定的轮廓精度。

上述实验结果表明,本文提出的基于数字孪生的轮廓误差抑制方法具有可行性。与传统的轮廓误差抑制方法和技术相比,本文构建的轮廓误差抑制技术框架,创新性地引入数字孪生技术,利用数字孪生的虚实交互、同步演化等优势特点,实现了轮廓误差的“建模—预测—控制”闭环抑制,并且能够在数控机床中得以应用。
通过与文献[4,15-16]的实验结果对比,本文所提方法和传统方法均能将轮廓误差控制在十几到几十微米范围内。然而,受现有数控系统CPU和通讯性能所限,本文实验中,数字-物理空间的通讯间隔较大,暂时无法实现插补周期内的虚实同步。因此,对于包含尖角、变曲率等特征的复杂参数曲线轨迹,暂时难以对其轮廓误差进行有效抑制。鉴于本文所提方法和技术框架在轮廓误差抑制方面具有潜在优势,提高数字-物理空间的通讯频率和数字孪生体的运行效率,将是后续研究的重点。
4 结束语
本文针对轮廓误差抑制领域的瓶颈问题,提出了基于数字孪生的轮廓误差抑制方法,并构建了面向轮廓误差的“建模—预测—控制”闭环抑制技术框架。详细阐述了针对该方法的4项关键技术:高保真数字孪生体建模、虚实精确同步、轮廓误差高置信动态预估以及轮廓误差综合抑制,并在某小型三轴数控机床上进行了应用验证。结果表明,该方法能够实现数控机床的运动位移、速度以及加速度在数字空间和物理空间中的低延时同步。对于常规的参数曲线轨迹,该方法能够实现轮廓误差的有效抑制。通过与传统轮廓误差抑制方法进行对比分析,数字孪生在改善轮廓误差控制精度和插补效率方面具有明显的优势,后续研究将围绕提高数字—物理空间虚实同步的实时性开展,并针对如何将大数据、人工智能等技术与数字孪生技术相结合进行深入研究,进而提高数字孪生体运行效率。

