Peakon,Pseudo Peakon,Periodic Peakon and Compacton Determined by Exact Solutions of Singular Nonlinear Traveling Wave Systems

Li Jibin

(1.School of Mathematical Science,Huaqiao University,Quanzhou,Fujian362021,China;2.Department of Mathematics,Zhejiang Normal University,Jinhua,Zhejiang321004,China;3.Department of Mathematics,Kunming University of Science and Technology,Kunming,Yunnan 650093,China)

Abstract In this paper,we first study the exact peakon,periodic peakon,pseudo peakon as well as the compacton solutions for the generalized Camassa Holm equation and the Degasperis Procesi equation.Based on the method of dynamical systems and the theory of singular traveling wave equations,the exact explicit parametric representations of the above mentioned solutions are derived.These solutions tell us that peakon is a limit solution of a family of periodic peakons or a limit solution of a family of pseudo peakons under two classes of limit senses.The pseudo peakon and pseudo periodic peakon family are smooth classical solutions with two time scales.

Key words Nonlinear wave equation Traveling wave solution Bifurcation Pseudo peakon Periodic peakon Compacton Exact solution Peakon

1 Introduction

In recent thirty years,nonlinear wave equations with non smooth solitary wave solution(so called peakon)attract much attention in the literature.Peakon was first proposed by Cammasa and Holm[1,2],and thereafter other peakon equations were developed(see Degasperis and Procesi[3],Degasperis,Holm and Hone[4],Qiao[5,6],Li and Dai[7],Novikov[8],and cited references therein).Peakons are the so called peaked solitons,i.e.,solitons with discontinuous first order derivative at the peak point.Usually,the profile of a wave function is called peakon if at a continuous point its left and right derivatives are finite and have different sign(see Fokas[9]).

We emphasize that peakon is a special traveling wave solution of a nonlinear model(a PDE).Therefore,it is very important to study the dynamical behavior for the corresponding traveling wave system(an ODE)of the nonlinear model.

In Li and Qiao[10],the authors showed that there exists a pseudo peakon solution for nonlinear wave equations.The so called“pseudo peakon”means that the wave profile looks like peakon,but the solution still has continuous first order derivative.By using the dynamical system approach,it has theoretically been proved that if a boundary curve of a period annulus of a center contains a segment of the singular straight line of a traveling wave system,then,near this straight line,the parametric representation of every periodic orbit has two time scales.In fact,for a singular nonlinear traveling wave system of the first class,the following two results hold(see Li and Dai[7],Li and Chen[11],and Li[12]).

Theorem1.1(The rapid jump property of the derivative near the singular straight line)Suppose that in a left(or right)neighborhood of a singular straight line there exist a family of periodic orbits.Then,along a segment of every orbit near the straight line,the derivative of the wave function jumps down rapidly on a very short time interval.

Theorem1.2(Existence of finite time interval of solution with respect to wave variable in the positive or negative direction)For a singular nonlinear traveling wave system of the first class with possible change of the wave variable,if an orbit transversely intersects with a singular straight line at a point or it approaches a singular straight line,but the derivative tends to infinity,then it only takes a finite time interval of the wave variable to make moved point of the orbit arrive on the singular straight line.

In order to understand rigorously the occurrence of“peaked”traveling wave solutions and the change of wave profiles with the changes of the system parameters and level curves,we hope to obtain exact parametric representations of traveling wave solutions for a given nonlinear partial differential system.Using exact solution formulas to draw the wave profiles,we can see how to change of wave profiles.In section2of this paper,we take the following two nonlinear wave equations as examples to achieve this goal.

1.The generalized Camassa Holm(CH)equation with real parametersκ,α:

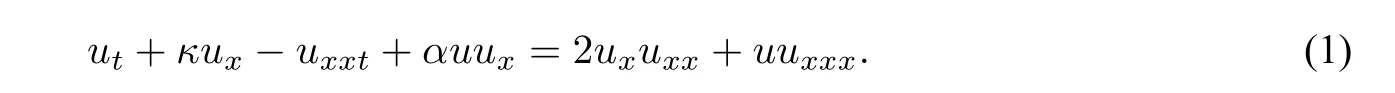
Equation(1)withα=3is exactly the standard CH equation[1]as a shallow water model.

2.The generalized Degasperis Procesi(DP)equation with real parametersκ,α:

Equation(2)withα=4is exactly the standard DP equation[3]as a shallow water model.

Letu(x,t)=ϕ(x−ct)=ϕ(ξ),then,equation(1)and(2)have the following traveling wave systems:

where we take the integral constants as zero.Two systems have the first integral,respectively,as follows:

The traveling wave systems(3)and(4)of equations(1)and(2)have a singular straight lineϕ=c.Under some parameter conditions,there exists at least one family of periodic orbits such that the boundary curves of the period annulus are a homoclinic orbit,a curve triangle or a arch curve(see the phase portraits in sections2).Applying the classical analysis method,we can obtain the parametric representations for these boundary curves.When we see these homoclinic orbit,arch curve and curve triangle into account as the limit curves of periodic orbit family in period annulus,these exact parametric representations provide very good understanding for the occurrence of peaked traveling wave solutions.Namely,the homoclinic orbit gives rise to a solitary peakon like wave solution(called pseudo peakon),a arch curve gives rise to a periodic peakon,while the curve triangle gives rise to a peakon solution.

How to classify traveling wave solutions seems kind of interest for a given traveling system.Lenells[13–16]studied traveling wave solutions for some nonlinear shallow water wave models admitting smooth,peaked,and cusped solutions,stumpons,as well as composite traveling wave with a fractal appearance.The author introduced the concept of distribution to understand peaked wave solutions.In fact,because the corresponding traveling wave equations of considered models are integrable planar dynamical systems,these models can not have so called composite traveling wave with a fractal appearance.Similar incorrect understand appeared in Geyer et al.[17],they stated that a shallow water wave model has“Cantor wave with peak elements and cusp elements”.

By adopting the method of dynamical systems with Theorem1.1 and Theorem1.2 ,we can obtain dynamical behavior of all traveling wave solutions to integrable PDE models.Therefore,we know which orbit gives rise to what wave profiles and how the wave profiles are changed depending on the parameters.In addition,applying the first integrals of the integrable traveling wave systems,we are able to get some exact explicit solutions(see Li et al.[18–21]and Li[11]).

Li et al.[18]showed the following two conclusions:(A)Under different parameter conditions,one nonlinear wave equation can have different exact one peakon solutions.(B)Different nonlinear wave equations can have different explicit exact one peakon solutions.Namely,there are various exact explicit one peakon solutions,which are different from the peakon solution given by equation(1)and(2).

This paper is organized as follows.In sections2,we first discuss the bifurcations of phase portraits and derive the exact solutions for the traveling wave systems of equations(1)and(2),respectively.The obtained result is used to study the classification of traveling wave solutions.In section3,we use three nonlinear wave equation models to show that there exist various exact explicit peakon solutions,which are different from the peakon solutions given by the generalized Camassa Holm equation and the Degasperis Procesi equation.In section4,we show that so called“peakon equations”in some references have no peakon.Because corresponding to these“peakon equations”,their traveling systems are singular traveling systems of the second kind(see Li[11]),which can not have the peakon solution.

2 Exact peakon,pseudo peakons,periodic peakon and compacton solutions of CH and DP equations

2.1 The bifurcations of phase portraits of system(3)and(4)

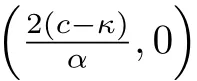
Making the transformation dξ=(ϕ−c)dζforϕ̸=c,system(3)becomes its regular associated system[10]:

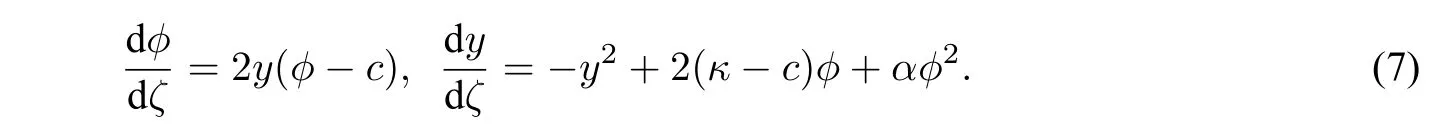
By the theory of planar dynamical systems,we obtain the bifurcations of phase portraits of system(3)for a fixedc＞0which are shown in Figure1.

Second,we consider the regular associated system of system(4):

By the theory of planar dynamical systems,we obtain the bifurcations of phase portraits of system(4)for a fixedc＞0which are similar to Figure1.

Figure1 Bifurcations of phase portraits of system(3)for α̸=0,β=κ−c

2.2 Exact pseudo peakon,pseudo periodic peakon solutions of CH and DP equations

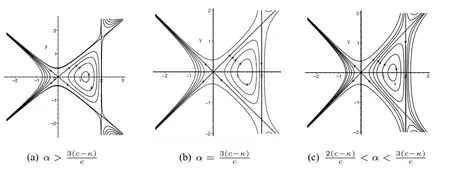
Figure2 The phase portraits of(3)for α＞0,β=κ−c＜0

Let us first consider the parametric representations of the bounded orbits given by Figure2(a).

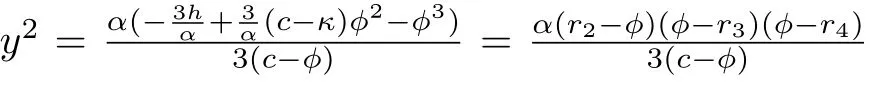
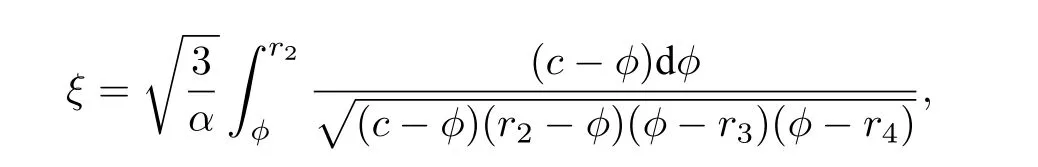
which leads to the parametric representation

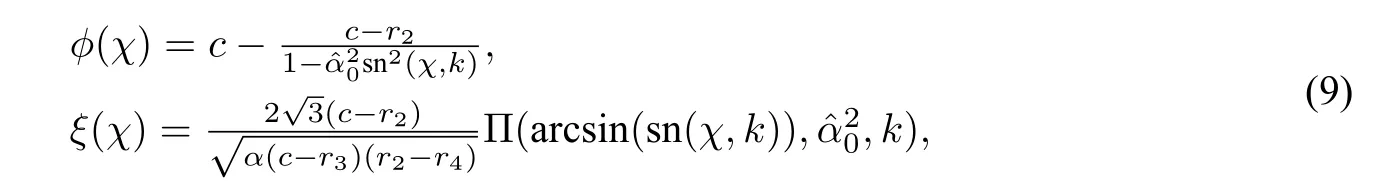
In addition,from(9),one can easily see that

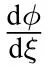
which leads to the parametric representation

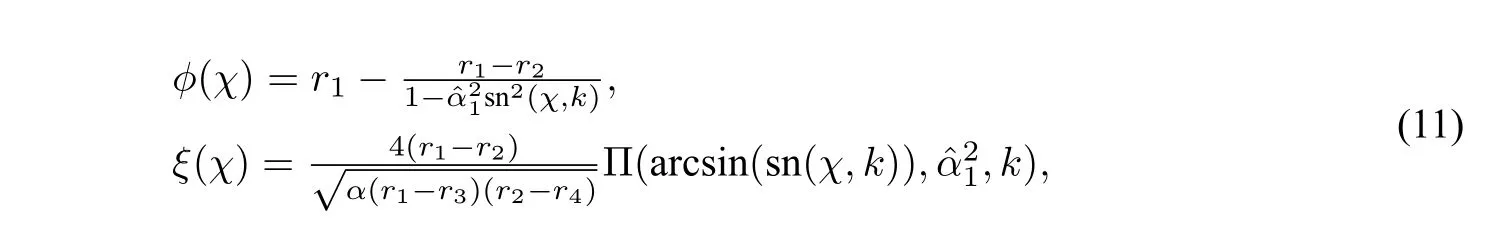
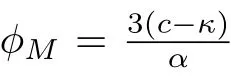
forχ∈(−∞,0]and forχ∈[0,∞),respectively.

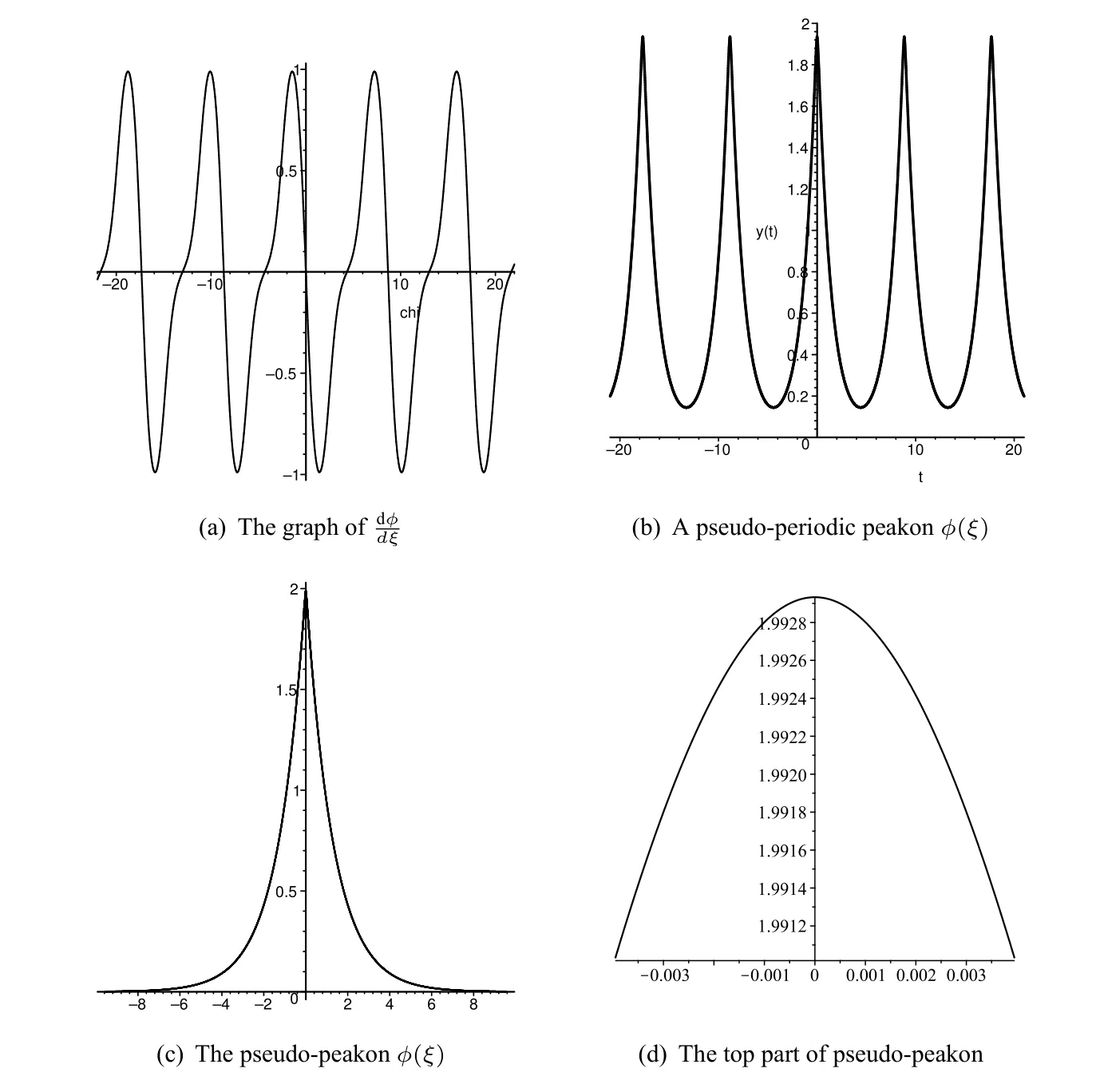
Figure3 The changes of wave profiles of ϕ(ξ)

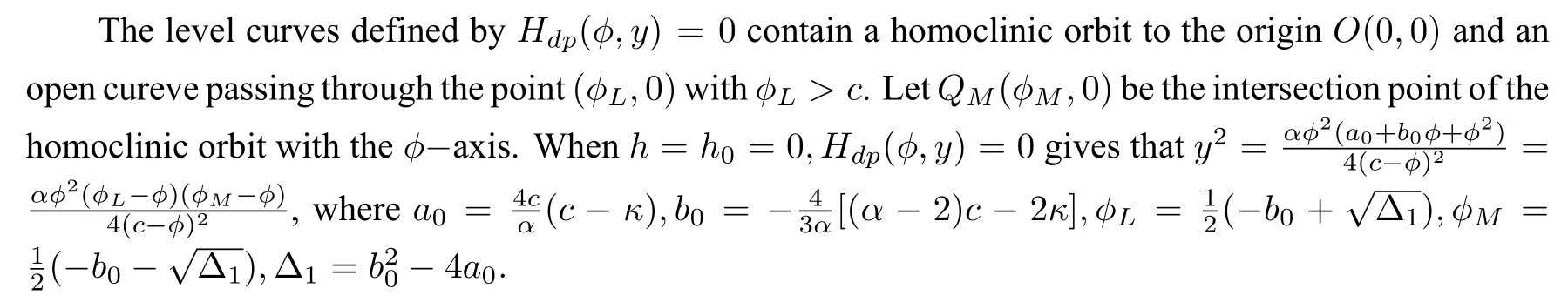
By using the first equation of system(4)and taking initial valueϕ(0)=ϕM,we obtain the parametric representation of the homoclinic orbit to the originE0(0,0)defined byHdp(ϕ,y)=0as follows:

2.3 Exact peakon solutions of CH and DP equations

(i)For the family of periodic orbits of system(3)and(4)defined byHch(ϕ,y)=h,h∈(0,h1)andHdp(ϕ,y)=h,h∈(h1,0)in Figure2(b),we have the same parametric representation as(9)and(11).

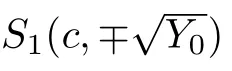
Forsystem(3),corresponding tothetwostraightlineorbitsconnectingthe equilibriumpointsO(0,0)definedbyHch(ϕ,y)=0,wehavey2=αϕ2.By theorem1.2insection1,wecan take initial value asϕ(0)=c.Then,we have which is a real peakon solution to CH equation(1)(see Figure4(b)).

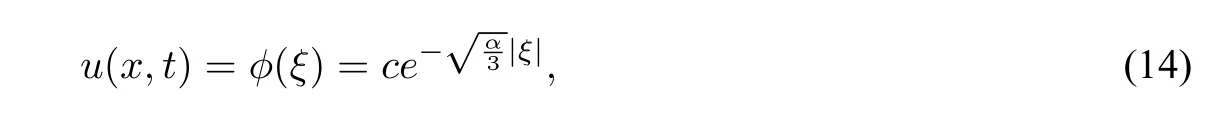
Figure4 The peakon of CH equation

2.4 Exact periodic peakon solutions of CH and DP equations given by arch curves and compacton families

We discuss the exact solutions for the orbits shown in Figure2(c).

(i)For the family of periodic orbits of systems(3)and(4)defined byHch(ϕ,y)=handHdp(ϕ,y)=h,h∈(hs,h1),respectively,we have the same parametric representations as(9)and(11).

(ii)For the arch orbit defined byHch(ϕ,y)=hsandHdp(ϕ,y)=hs,we havey2=(cm0+m0ϕ+ϕ2),wherem0=c−(c−κ)andy2=(cm1+m1ϕ+ϕ2),wherem1=[(α−4)c+4κ],respectively.Hence,we obtain the parametric representation of the periodic peakon wave solution of CH equation as follows(see Figure5(a)):

and the periodic peakon solution of DP equation(2)as follows:

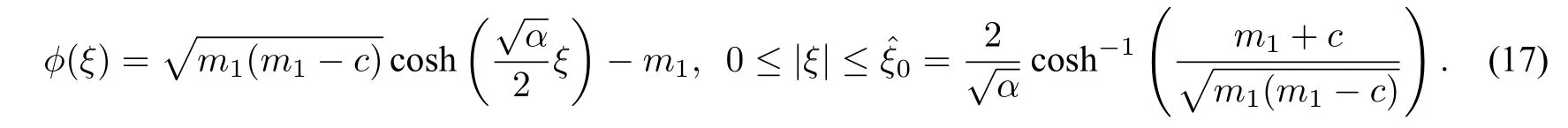
which leads to the parametric representation(see Figure5(b)):

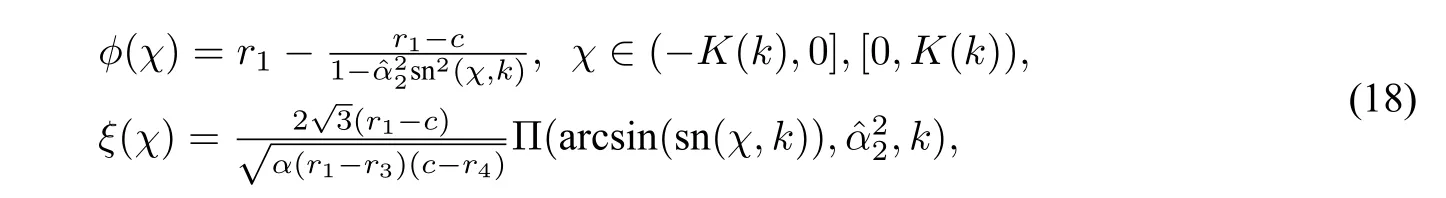
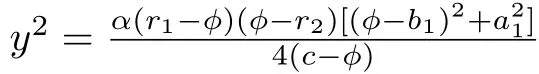
which leads to the parametric representation

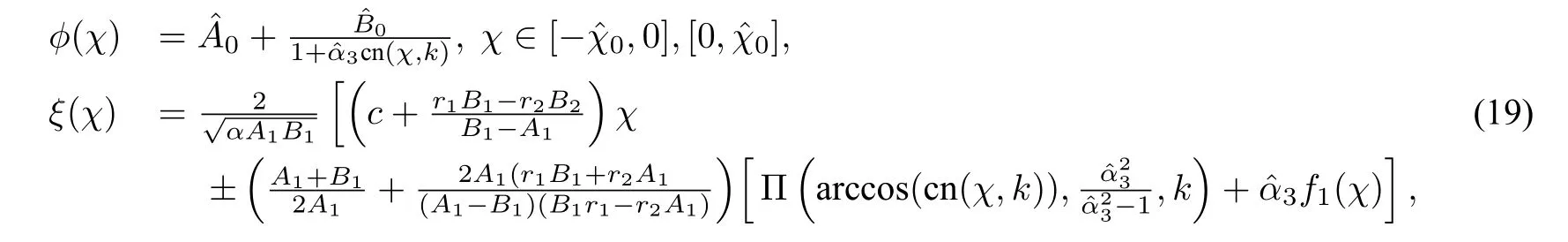
(18)and(19)give rise to,respectively,a family of compacton solutions of CH equation(1)and DP equation(2).We can see that the compacton family is a solution family of a singular system for which all solutionsϕ(ξ)have finite support set(see Olver and Rosenau[23]),i.e.,the defined region of everyϕ(ξ)with respect toξis finite and the value region of functionϕis bounded(see Figure5(b)).Some references call these solutions as“breaking wave solutions”,becauseξis not∈(−∞,∞).

(iv)The level curves defined byHch(ϕ,y)=0contain the stable and unstable manifolds of the saddle pointO(0,0)and a open curve passing through((c−κ),0).For the right stable and unstable manifolds,we have.On the basis of Theorem1.2 in section1,we can take initial valueϕ(0)=c.Using the first equation of(3),we have the following two exact solutions(see Figure5(c),(d))of CH equation(1):

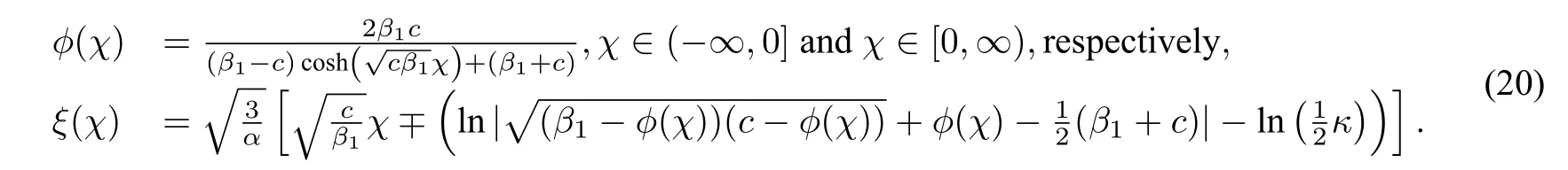
Notice that in some references,the authors compose the two solutions of stable manifold and unstable manifold as a cuspon solution.We see from Figure5(c),(d)that the CH equation and DP equation have no so called cuspon solution.

Figure5 The peakon of CH equation

To sum up,we obtain the following result.

Theorem2.1For the generalized Camassa Holm equation(1)and the Degasperis Procesi equation(2),considering their traveling wave system(3)and(4)with the wave velocity parameterc＞0fixed,the following conclusions hold.

Remark2.1Theorem2.1 answers the question what are the geometry of peakon and periodic peakon.Namely,

(A)As the bounded curves of a periodic anulus of a center,a curve triangle consisting of three segments of the stable and unstable manifolds of a saddle point and a singular straight line gives rise to a peakon solution.

(B)As the bounded curves of a periodic anulus of a center,the arch curves consisting of an arch curve and a segment of a singular straight line give rise to a periodic peakon solution.

Remark2.2We can see from Figure1(d),(e),(f)that whenβ=κ−c＞0andα＞0,there exist similar three phase portraits as Figure2.If we make the originO(0,0)in Figure2move toE1(ϕ1,0),we have the same phase portraits as Figure1(d),(e),(f).Hence,by shifting−ϕ1in the above exact solution formulas,we obtain new exact solutions.

Remark2.3We generally consider the planar dynamical system

withδ̸=1,2,system(22)has the first integral

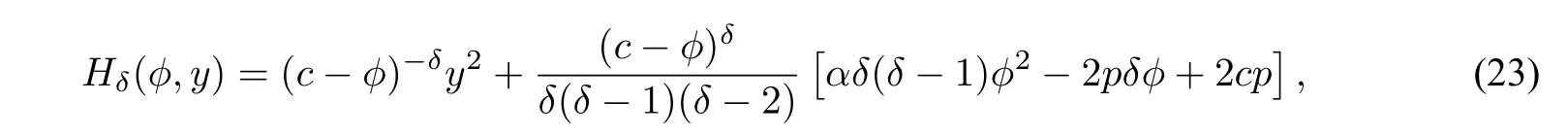
wherep=cα−(δ−2)(κ−c).Whenδ=−1,−2,we obtainHch(ϕ,y)andHdp(ϕ,y),respectively.

3 Variform exact peakon solutions for some nonlinear wave models

In this section,we discuss the exact peakon solutions for three nonlinear wave models.

3.1 Exact peakon of modified Serre shallow water wave equations

Consider the following modified Serre equation(see[24 26]):

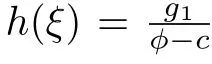
System(26)has the following first integral:

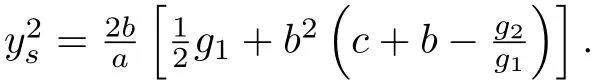
Figure6 Two phase potraits of system(26)

We next consider the exact parametric representations of peakon solutions of(26),which correspond to the curve triangles in Figure6(a),(b).

We see from(27)that

Note that,whenh=hs,one has

(ii)Second,consider the two curve triangles in Figure6(b),which are defined by the level curvesH2(ϕ,y)=hs=h3.

Corresponding to the left curve triangleEcS+S−,as a limiting solution of a family of homoclinic orbits,ash→hs,it gives rise to an anti peakon,which has the parametric representation(see Figure7(c)):

Corresponding to the right curve triangleS+E3S−,as a limiting solution of a family of periodic orbits enclosing the centerE2(ϕ2,0),ash→hs,it gives rise to a peakon,which has the following parametric representation(see Figure7(d)):

Figure7 Three wave profiles of system(26)

3.2 Peakon of the multicomponent Korteweg de Vries equation with dispersion

In1985,Kupershmidt[27]posed the following equations:

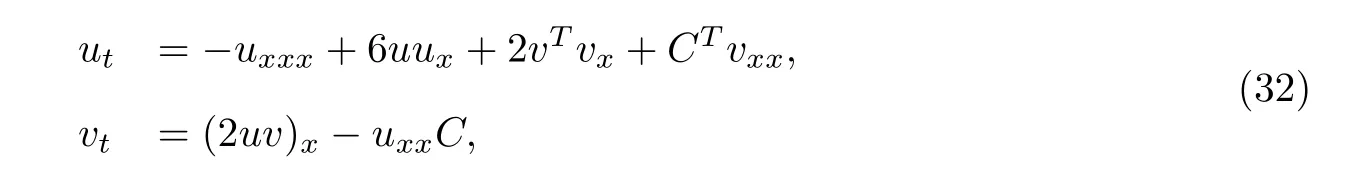
wherev=(v1,v2,···,vn)TandC=(c1,c2,···,cn)Tis a constant(column)vector.System(32)is a bi Hamiltonian system with an infinite number of conservation laws.

To investigate the traveling wave solutions of system(32),let

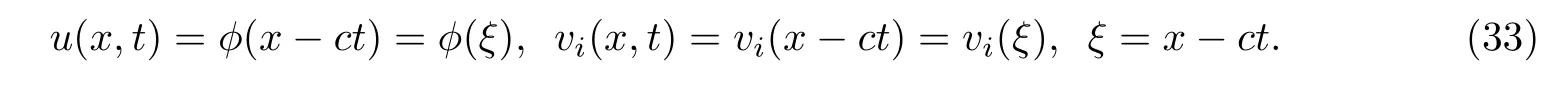
Substituting(33)into the second equation of system(32)and integrating the obtained equation once,we have

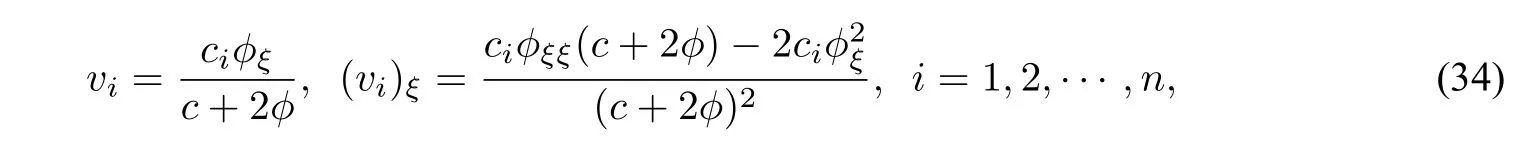
where we take the integral constant as zero.

Substituting(34)into the first equation of system(32)and integrating the obtained result once,we obtain the planar dynamical system(see[28]):

which has the first integral

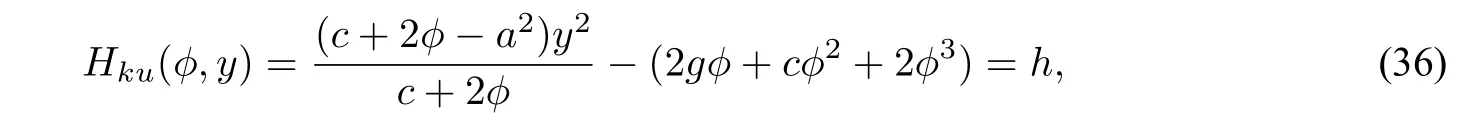
wherehandgare two constants.

Consider the associated regular system of system(35)as follows:

For the first integral given by(37),we write that

and

Figure8 The curve triangle defined by Hku(ϕ,y)=hs of system(32)

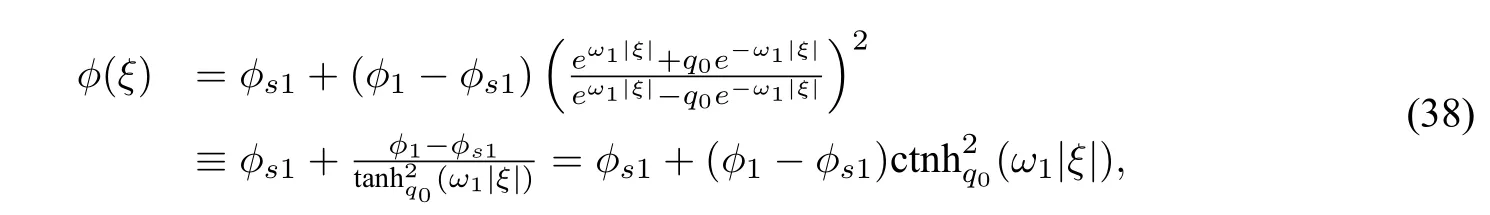
3.3 Peakon of the rotation two component Camassa Holm system

Consider the rotation two component Camassa Holm system(see[31],[32]):

To investigate the traveling wave solutions of system(39),by letting

u(x,t)=ϕ(x−ct)=ϕ(ξ),ρ(x,t)=v(x−ct)=v(ξ),

where,whereβis an integration constant andβ̸=0.By the first equation of system(39),we have

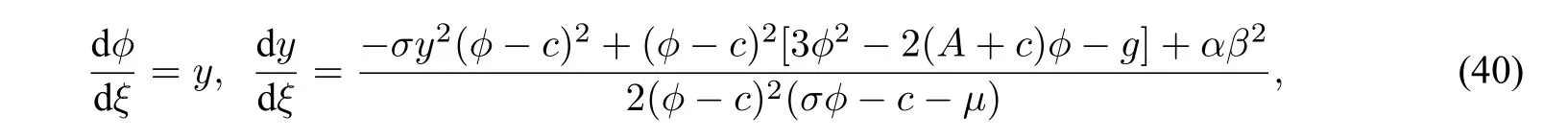
which has the following first integral:

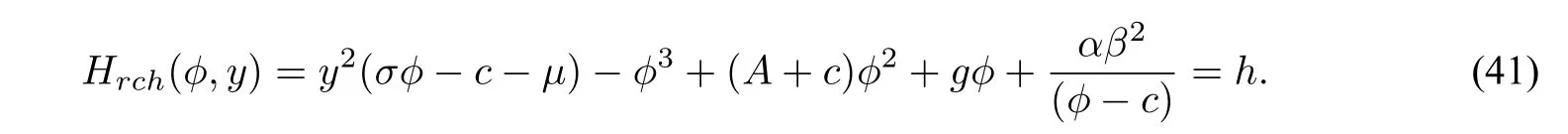
We next discuss the exact parametric representations of peakon and anti peakon solutions of system(40)corresponding to two curve triangles in Figure9(a)and(b).As can be seen from(41),for a fixed

Figure9 Phase portraits and curve triangle defined by Hrch(ϕ,y)=hs of system(40)

integral constanth,one has

By using the first equation of system(40)and taking integration along a branch of the level curve defined byHrch(ϕ,y)=hwith initial valueϕ(ξ0)=ϕ0,one obtains

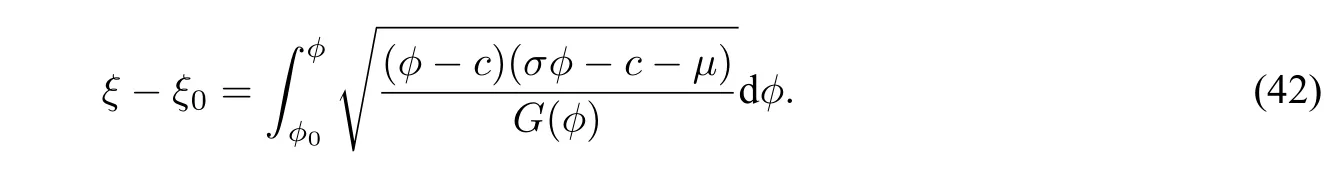
Hence,taking integrals along the curvesE3S+andS−E3,it yields from(42)that

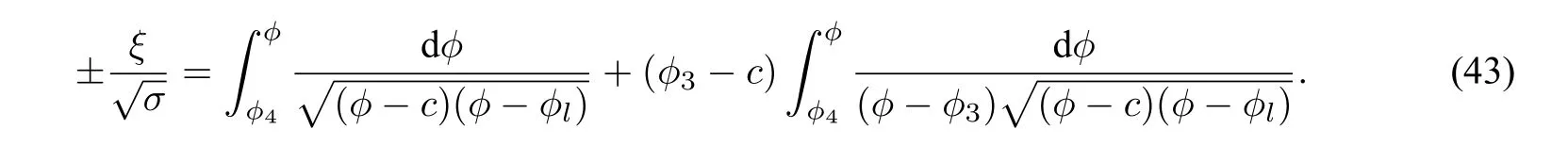
Thus,one obtains the following exact peakon solution of system(40)(see Figure9(d)):

where

(ii)Corresponding to the orbit triangle(see Figure9(b))connecting the equilibrium pointsE4(ϕ4,0)andS∓of system(40)and enclosing the centerE3(ϕ3,0)in Figure9(b),which is the level curve defined byHrch(ϕ,y)=hs=h4,one hasG(ϕ)=(ϕ4−ϕ)2(ϕ−(ϕ−ϕl).

Then,taking integrals along the curvesS+E4andE4S−,it yields from(42)that

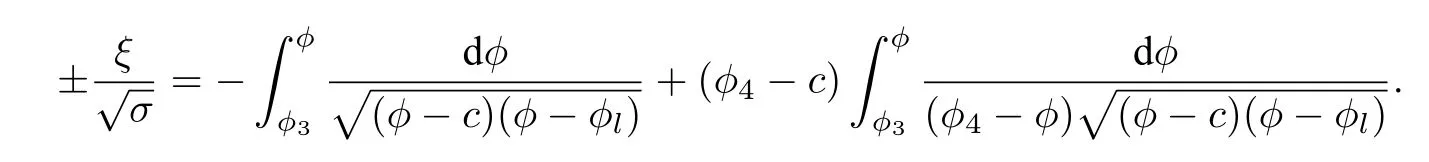
Thus,one obtains the following exact anti peakon solution of system(40):

where

4 So called“Peakon equations”have no peakon

In2019,Anco and Recio[33],introduced a general family of peakon equations involving two arbitrary functions of the wave amplitude and the wave gradient,in which one parameter subfamilies of the CH mCH Hamiltonian family are explored.The authors suggested to study the following“family of Hamiltonian multi peakon equations”

which involves two arbitrary functionsf1andg1ofu2−u2x.

Two subfamilies represent nonlinear generalizations of the mCH equation given by

and

A unified generalization of these two subfamilies is

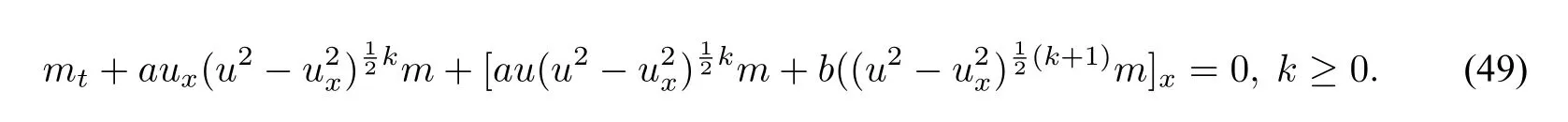
By puttingk=2p−2,b=0,a=1in the three parameter family(49),we obtain the one parameter family of generalized CH equation(47).Takinga=0,b=1,k=2p−1,equation(49)becomes equation(48).

The authors of[33]stated that“in the case of thep=2generalized mCH equation(47),the peakon and anti peakon can form a bound pair which has a maximum finite separation in the asymptotic past and future”.In[34–37],Anco et al.,studied other peakon equations.

Unfortunately,these authors did not derive the corresponding traveling wave systems of equations(47),(48)and(49).In this section,we consider the bifurcations problems of the solutions of the corresponding traveling wave systems of equations(47),(48)and(49)depending on the parameters of systems.

To study the traveling wave solutions of equations(47),(48)and(49),settingu(x,t)=u(x−ct)≡ϕ(ξ),whereξ=x−ctandcis the wave speed.Substituting it into(47),(48)and(49)and integrating the obtained equations once,we obtain

and

wheregis an integral constant.For equation(50),we suppose thatg̸=0.Otherwise,(50)becomes a linear equation.Equation(50),(51)and(52)are respectively equivalent to the planar dynamical systems

and

System(53),(54)and(55)have the first integrals,respectively,

and

Especially,whenp=1,system(53)becomes

with the first integral(see Li and Zhang[38])

Whenp=1,system(54)becomes the traveling wave system of Camassa Holm equation as follows:

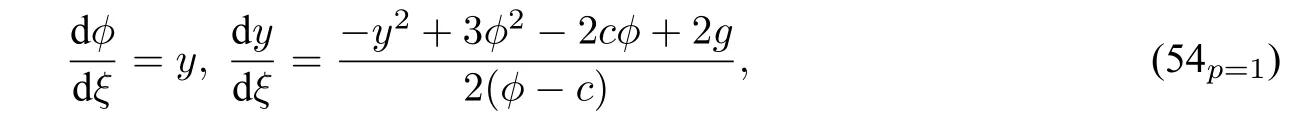
with the first integral

The bifurcations and exact solutions of system(54p=1)can be similarly seen in section2.So that,for equation(54),we only consider the casep≥2.

4.1 Bifurcation of phase portraits of systems(53),(54)and(55)

We always assume thatc＞0,g＞0andp≥1are positive integers.

4.2.1 We first consider all possible phase portraits of system(53).It is known that system(53)has the same invariant curve solutions as the associated regular system:

wheredξ=[c−(ϕ2−y2)p]dζ,forc−(ϕ2−y2)p̸=0.

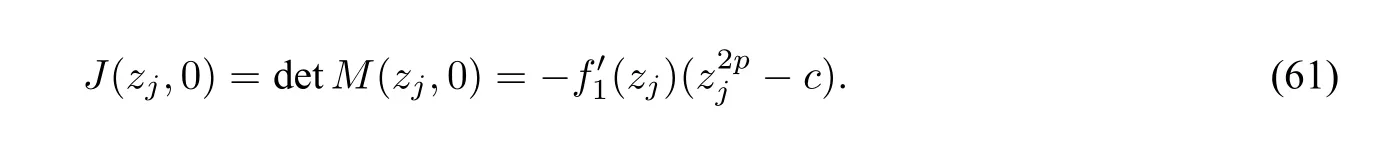
LetM(zj,0)be the coefficient matrix of the linearized system of(60)at an equilibrium pointEj(zj,0).We have By the theory of planar dynamical systems,for an equilibrium point of a planar integral system,ifJ＜0,then the equilibrium point is a saddle point;ifJ＞0,then it is a center point;ifJ=0and the Poincaré index of the equilibrium point is0,then this equilibrium point is a cusp.

We write thathj=Hp1(zj,0),j=1,2,3whereHp1is given by(56).

Wheng＜0,the bifurcations of phase portraits of system(53)are just the reflections of Figure10(a) (e)with respect to they−axis.Therefore,we only need to discuss the caseg＞0.

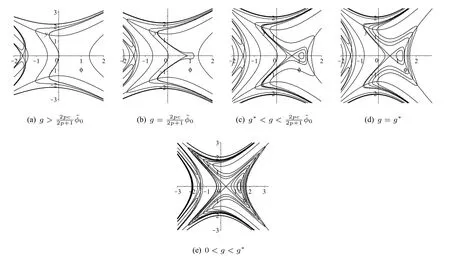
Figure10 The bifurcations of phase portraits of system(53)for a fixed c＞0,p≥1

4.2.2 We next consider all possible phase portraits of system(54).System(54)has the same invariant curve solutions as the associated regular system:

wheredξ=[c−ϕ(ϕ2−y2)p−1]dζ,forc−ϕ(ϕ2−y2)p−1̸=0.

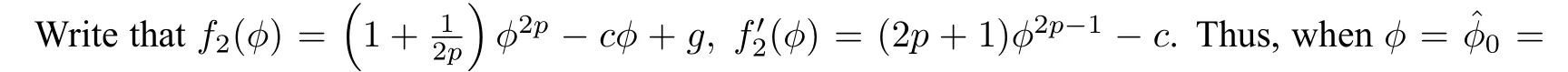
The equilibrium pointsEj(zj,0)of system(62)satisfyf2(zj)=0.It is easy to show for a fixedc＞0,the following facts hold.

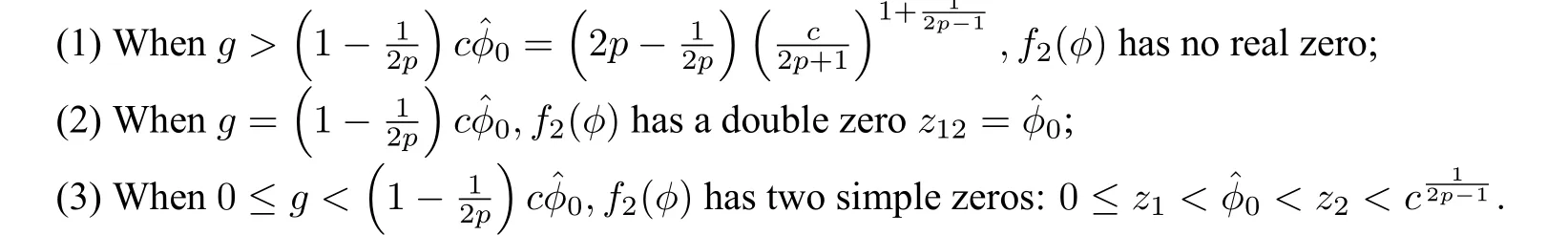
LetM(zj,0)be the coefficient matrix of the linearized system of(62)at an equilibrium pointEj(zj,0).We have

We write thathj=Hp2(zj,0),j=1,2whereH2is given by(57).

By using the above result to do qualitative analysis,with the change of the parameterg,we have the bifurcations of phase portraits of system(54)shown in Figure11.We also draw the graph of the hyperbolaϕ(ϕ2−y2)p−1−c=0in every phase portrait in order to show the position of the singular curve.

Figure11 The bifurcations of phase portraits of system(54)for a fixed c＞0,p≥2

4.2.3 We now consider all possible phase portraits of system(55).System(55)has the same invariant

curve solutions as the associated regular system:

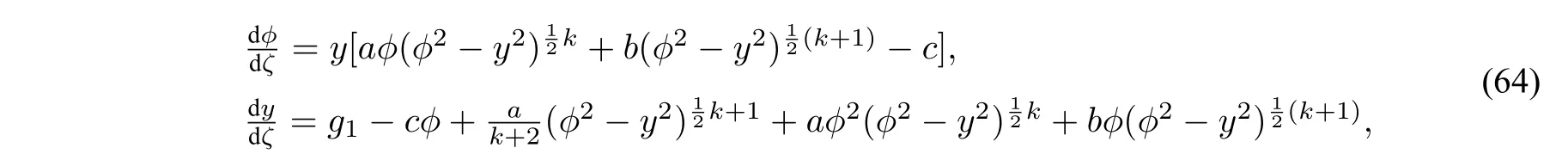
The equilibrium pointsEj(zj,0)of system(64)satisfyf3(zj)=0.It is easy to show for a fixedc＞0,the following facts hold.

LetM(zj,0)be the coefficient matrix of the linearized system of(18)at an equilibrium pointEj(zj,0).We have

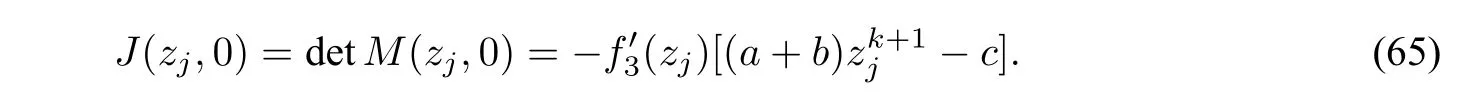
We write thathj=Hk(zj,0),j=2,3whereHkis given by(58).

By using the above result to do qualitative analysis,with the change of the parameterg,we have the bifurcations of phase portraits of system(55)like Figure11whenkis an even number.Whenkis a odd number,the bifurcations of phase portraits of system(55)are like Figure10.

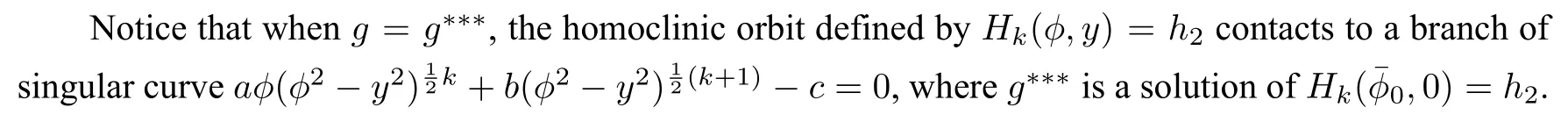
4.2 The solitary wave solutions determined by the homocinic orbits of systems(53),(54)and(55)

It is well known that a smooth homoclinic orbit of a traveling system gives rise to a solitary wave solution of the corresponding nonlinear wave equation.We always assume thatc＞0and is fixed.

Theorem4.1Assume thatc＞0is fixed.

Forp=1,to find the exact explicit parametric representation of solitary wave solution,we have from(56p=1)that

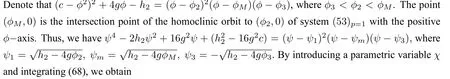
Thus,we have the following exact explicit parametric representations of smooth solitary solution of the system(53p=1)(see Li and Zhang[38]):

Forp≥2,because we can not explicitly solve the exactyfromHp1(ϕ,y)=h2,therefore,we can not give the exact solitary wave solutions of equation(53).

4.3 The M shape traveling wave solutions determined by the homocinic orbit of sysems(53),(54)and(55)

Figure12 The graph of(ϕ2−y2)p−c=0and the vector fields defined by(60)and(53)

Similarly,we can discuss the vector fields for systems(54)and(62).

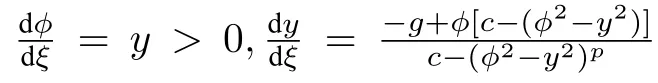
Figure13 M−shape wave solution of system(60)in the(ζ,ϕ)−plane when0＜g＜g∗

Figure14 The M shape wave consisting of three breaking waves of system(53)

The above statement is also holds for the systems(54)and(62).

Whenp=1in system(53),the exact parametric representation ofMshape wave solution had been given in Li and Zhang[38]and Li[11].

To sum up,we has the following conclusion.

Theorem4.2Assume thatc＞0is fixed.

(i)When0＜g＜g∗,equation(53)has aM−shape wave solution defined by a branch of the level curvesHp1(ϕ,y)=h2,which consists of three breaking wave solutions.

(ii)When0＜g＜g∗∗,equation(54)has aM−shape wave solution defined by a branch of the level curvesHp2(ϕ,y)=h1,which consists of three breaking wave solutions.

(iii)When0＜g＜g∗∗∗,equation(55)has aM−shape wave solution defined by a branch of the level curvesHk(ϕ,y)=h2,which consists of three breaking wave solutions.

We see from the discussion of this section that for the singular travelling wave systems of the second class,the dynamics of the orbits are different from the singular travelling wave systems of the first class.Because every singular curve intersects an orbit of the singular travelling wave systems of the second class only in a few isolated points,so that in systems(53)and(60),the variablesξandζhave the same“time scale”.The singular curves make the direction of vector field defined by the singular travelling wave systems of the second class swiftly change.It derives new breaking wave solutions.Equation(53),(54)withp≥2and(55)have no peakon solution in the sense of peakon in the Camassa Holm equation.Therefore,a lot of new peako models posed by some authors(for example,in[34–36])need to make new studies for their traveling wave systems.