基于CFD 的空气喷射器辅助结构研究

周三平，张旭坤

（西安石油大学机械工程学院，陕西 西安 710065）

喷射器是将工作流体所携带的能量传递给引射流体的装置，其最大特点是能够提高流体的压力而不消耗机械能，常用于高压流体抽吸低压流体的场合，由于没有机械传动部件，具有不消耗机械能、结构简单、运行稳定、维修便捷等优点，现已广泛应用于机械、石油化工、制冷、轻工等行业。

喷射器的研究有非常久远的历史。早在20 世纪末，G.Zenner 和M.Rankin 就基于混合的流体应用动量方程，提出了喷射器的理论基础[1]，在后来的研究中被广泛引用，并用实验加以验证。但是该理论存在一定的缺陷，不能够完全解决喷射器的计算问题，诸如喷射器的剖面形状、轴向尺寸等。随着流体力学和气体动力学研究的深入，喷射器的普遍性理论和计算方法被建立起来[2]，随后Elord、Dutton、Keenan 和Neumann 等一大批学者对喷射器的设计和理论做了进一步的完善[3-7]。现有的喷射器的设计方法，主要是前苏联的索科洛夫提出的一整套设计方法[8]，国内学者陆宏圻也出版总结了研究成果并阐述了理论体系[9]，但是这些理论并不能适用于所有的喷射器结构和工况。针对此问题，陈洪杰等人[10]引入单相及两相流声速计算模型，提出了基于实际气体的圆柱形混合室喷射器设计方法，周三平等人[11]则对喷射器的气体动力函数法的真实气体做了修正。这些研究在一定程度上完善了喷射器的设计理论。基于动力学函数的索科洛夫设计方法，只对横截面积进行了设计，对轴向长度基本都是基于经验数据得出的，所以在采用索科洛夫设计方法对喷射器进行设计之后，需要对所设计的喷射器的结构进行优化。

本文采用索科洛夫设计方法，先对空气喷射器的初始尺寸进行设计，再利用计算流体力学数值模拟软件Fluent，对该喷射器的喷嘴距、混合室长度和喷嘴喉部长度等轴向尺寸对喷射器性能的影响，进行了计算流体力学数值模拟，以获取空气喷射器的最佳轴向长度。

1 喷射器初始尺寸确定

喷射器主要由喷嘴、吸入室、混合室、扩压器等部分组成，结构如图1 所示。选用索科洛夫提出的基于气体动力学函数法的经验公式，对喷射器的初始尺寸进行设计。工作流体温度为200℃，压力为5MPa；引射流体温度为20℃，压力为20kPa，流量大于25kg·h-1；混合流体出口压力为50kPa。依据索科洛夫经验公式，设计的喷射器的各结构尺寸如表1 所示。

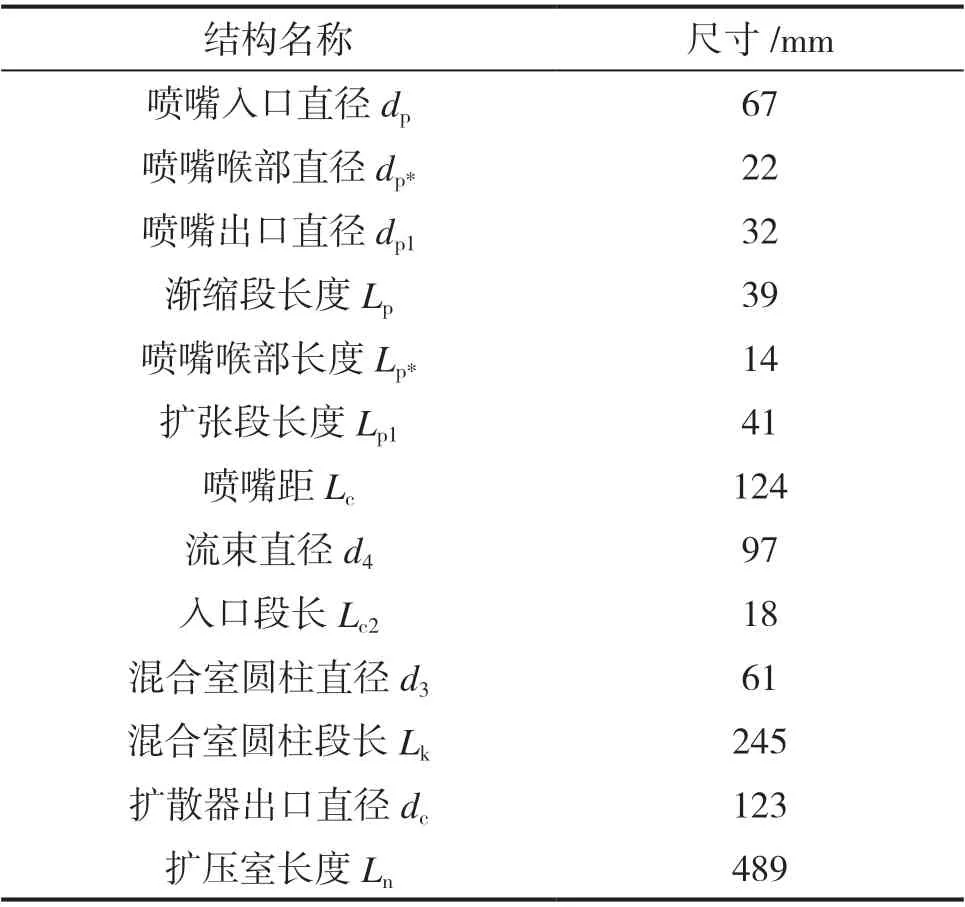
表1 空气喷射器结构尺寸计算结果

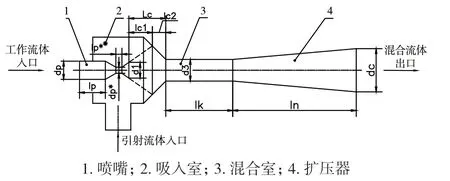
图1 空气喷射器结构简图

2 基于CFD 的空气喷射器辅助设计

采用计算流体力学数值模拟软件，对基于索科洛夫设计方法得出的喷射器的喷嘴距、混合室长度和工作喷嘴喉部长度等3 个轴向尺寸进行数值模拟，从而得出最佳轴向尺寸。

2.1 几何建模和网格划分

运用Ansys Workbench 中的Design Modeler 模块对空气喷射器进行建模，考虑到引射流体的速度相对于工作流体非常小，可以认为其对喷射器内部流场的影响可以忽略不计，因此将引射流体的径向入口改为轴向入口，此时喷射器结构为轴向对称结构，可以简化为二维结构并取一半的区域进行研究。为了提高网格精度，采用四边形结构网格，采用Mesh 模块进行网格划分，总体网格单元数176200个，部分网格结构如图2 所示。

图2 空气喷射器部分结构的网格划分

2.2 数学模型

对于空气喷射器，工作流体、引射流体及其混合流体的流动过程，遵守质量方程、能量方程和动量方程，如式（1）、（2）、（3）所示。

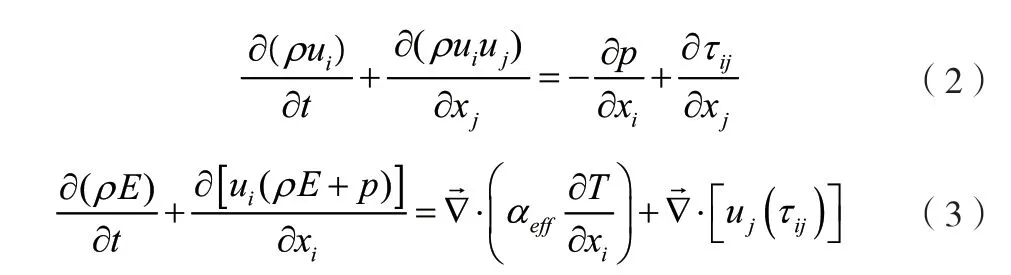
式中，ρ为密度；▽为哈密顿算子；T 为开氏温度，P 为压力；uij为速度在对应方向的分量；τ为切向速度；αeff为有效导热系数；τij为Reynold 应力项。

2.3 数值模拟方法与边界条件

采用Fluent 软件进行数值模拟，控制方程采用欧拉双流体模型，湍流模型采用Realizable k-ε，壁面用标准壁面函数，选择Coupled 算法进行算法迭代。为保证精度，动量方程、湍动能方程及湍流耗散率方程均采用二阶迎风格式离散。

喷射器的进出口均选用压力边界条件，工作流体入口5MPa，引射入口压力0.02MPa，混合流体出口压力0.05MPa。

2.4 喷射器的性能指标

喷射器性能可以用喷射系数来表征。喷射系数指的是引射流体与工作流体的质量流量之比，如式（4）所示。

式中，Gh为引射介质的质量流量，kg·s-1；Gp为工作介质的质量流量，kg·s-1，可以从模拟结果中读取。

3 数值模拟结果与分析

3.1 喷嘴喉部长度对喷射系数的影响

采用数值模拟方法，分别对喷嘴喉部长度Lp*为3.4mm、4.4mm、5.4mm、6.4mm、7.4mm、8.4mm 时的6 组数据进行了数值模拟，得到了喷嘴喉部长度对喷射系数的影响规律，结果见图3。由图3 可知，随喷嘴喉部的长度增加，喷射系数为先上升后下降，当长度为5.4mm 时，喷射器的喷射系数最大。

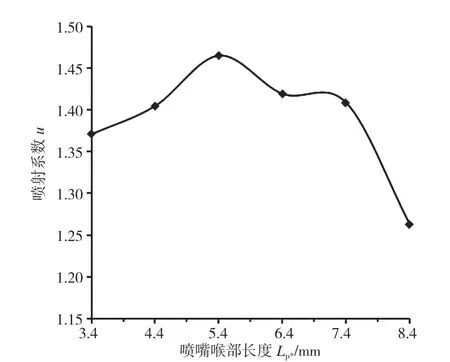
图3 喷嘴喉部长度对喷射系数的影响

3.2 喷嘴距对喷射系数的影响

采用数值模拟的方法，分别对喷嘴距Lc为64mm、74mm、84mm、94mm、104mm、124mm、134mm、144mm 时的8 组喷射器模型进行了数值模拟研究，获得了喷嘴距对喷射系数的影响规律，结果见图4。从图4 可以看出，当喷嘴距的长度在64～74mm 之间时，喷射系数u 随喷嘴距长度的增加而增大；喷嘴距的长度大于74mm 后，喷射系数u 随喷嘴距长度的增加而减小；喷射器的喷嘴距长度为74mm 时，喷射系数u 的值达到最大值。

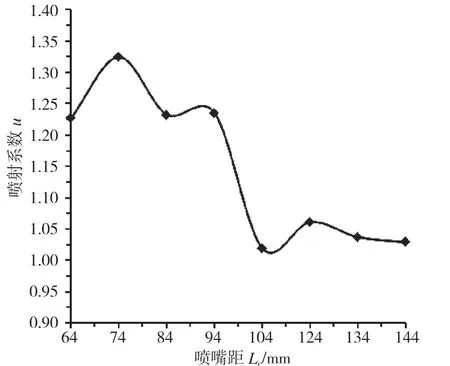
图4 喷嘴距对喷射系数的影响

3.3 混合室长度对喷射系数的影响

采用数值模拟方法，分别对混合室LK长度为250mm、255mm、260mm、265mm、270mm、280mm、300mm、310mm、320mm 的9 组数据进行数值模拟研究，得到混合室长度对喷射系数的影响规律，结果见图5。由图5 可以看出，喷射系数随混合室长度的增大而增大，达到300mm 以后，再逐渐减小。

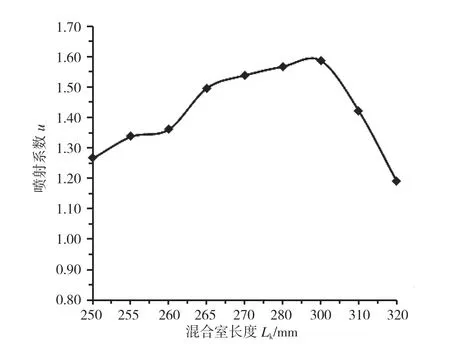
图5 混合室长度对喷射系数的影响

4 结论

1）喷嘴的喉部长度、喷嘴距和混合室长度对喷射系数的影响规律基本相似，喷射系数均先逐渐增大，达到最大值后再逐渐减小；

2）喷嘴的喉部长度、喷嘴距和混合室长度的最佳值分别为74mm、300mm 和5.4mm。与设计尺寸进行对比后可知，用索科洛夫设计方法所设计的喷射器并不是性能最好的。