如何正确运用χ2检验——Wald’s检验与SAS实现

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在构建广义线性回归模型、Cox比例和非比例风险回归模型的过程中，常涉及参数的检验问题，例如：检验部分或全部回归系数是否为0；还会涉及前述提及的各种情形下回归系数的区间估计问题；在处理复杂抽样设计定性资料时，可能会涉及一维频数分布表资料和二维频数分布表资料的独立性假设检验问题。本文介绍解决前述提及的三类问题所需要的Wald’s检验及其SAS实现。

1 Wald’s检验统计量的种类

1.1 一般Wald’s检验统计量和稳健Wald’s检验统计量

设logistic回归模型中只有一个自变量，则检验回归系数β是否为0，可用以下两个公式［1-3］之一：

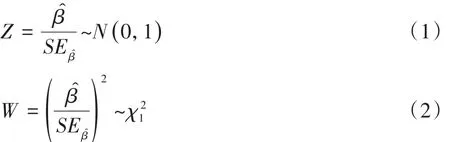
设logistic回归模型中的回归系数向量β具有K个分量，在SAS/STAT的PHREG过程中，给出的5个检验统计量（即似然比检验统计量、一般评分检验统计量、Wald’s检验统计量、稳健评分检验统计量和稳健Wald’s检验统计量）都服从自由度df=K的χ2分布。这5种检验都可以用于检验回归模型中全部回归系数是否都等于0，即H0：β=0。其中，一般Wald’s检验统计量和稳健Wald’s检验统计量的定义［4-5］如下：

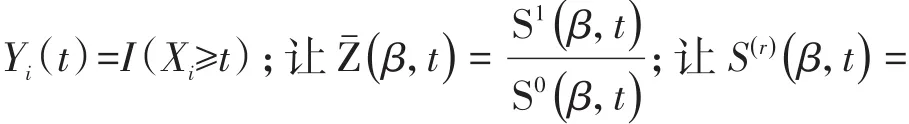
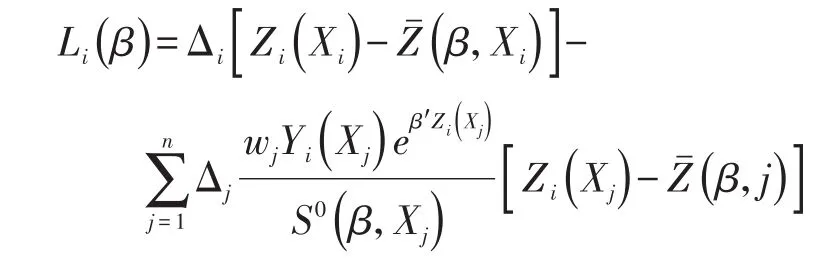
Binder于1992年将权重整合到分析之中，推导出β̂的稳健中间方差估计量：

式（5）中，I（β̂）是观测的信息矩阵，a⊗2=aa'。

注意：当wi≡1，V̂S（β̂）=D'D，此处，D是DFBETA残差矩阵（说明：DFBETA变量与回归分析资料中每一个观测有关，它是用来度量每个观测对回归系数影响大小的一个差量 δβ̂i= β̂- β̂（i），其中 β̂是全部观测所对应的回归系数或回归系数向量，而β̂（i）是第i个观测不在回归模型中所对应的回归系数或回归系数向量）。

【说明】Wald’s检验统计量可用于检验单个回归系数或全部回归系数是否为0；可用于检验已进入回归模型中的自变量是否可以被删除；还可用于估计回归系数的置信区间。

1.2 约束Wald’s χ2检验

关于回归系数β的线性假设可以表述如下：

式（6）中，L是线性假设的系数矩阵；c是常数向量；回归系数β的向量包含斜率参数和截距参数。与检验假设H0对应的约束Wald’s χ2检验统计量见式（7）：

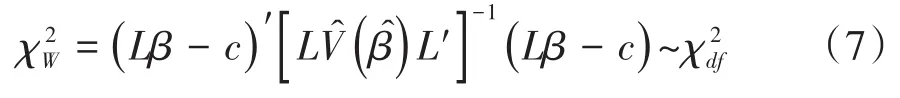
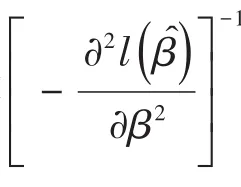
【说明】当取常数向量c=0时，此检验方法可用于检验回归模型中参数是否为0。

1.3 广义Wald’s检验统计量与广义Wald’s对数线性检验统计量

1.3.1 概述

在SAS/STAT的SURVEYFREQ过程中，针对复杂抽样设计（包括整群抽样和分层抽样）频数资料，有两种检验二维列联表资料中行、列两变量之间独立性假设的新方法，即广义Wald’s χ2检验与广义Wald’s对数线性χ2检验。其中，广义Wald’s χ2检验法是基于加权观察频数与加权期望频数之差量构造出来的；而广义Wald’s对数线性χ2检验法是基于对数优势比构造出来的。在构造这两种检验方法的过程中，都将复杂抽样设计考虑在内。在大样本条件下，前述提及的两种检验统计量均服从自由度df=（R-1）（C-1）的χ2分布。然而，依据实际的显著性水平和检验效能来考量，前述提及的两种检验方法已显示出较差的表现，特别是对于具有大的格频数或相对较小群数的二维列联表资料更是如此。为此，有多位统计学家提出了改进的建议，即采用F检验（用于2×2列联表资料）和校正F检验（用于非2×2列联表资料）。F检验和校正F检验比前述提及的两种χ2检验更稳定［4］。

1.3.2 广义Wald’s χ2检验统计量

在二维列联表资料中行、列两变量之间独立性假设成立的条件下，期望格频数的计算方法如下：

式（8）中，N̂r.与N̂.c分别代表第r行与第c列上估计的频数，N̂代表估计的总频数。总体加权频数等于期望频数的无效假设，可以采用下式表达：

式（9）中，r=1，2，…，（R-1），c=1，2，…，（C-1）。于是，广义Wald’s检验统计量的定义见下式：

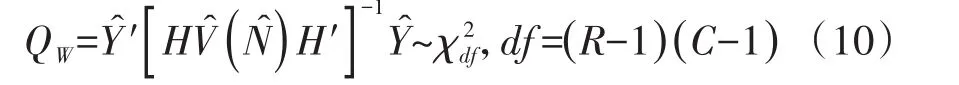
式（10）中，Ŷ是由（R-1）（C-1）个观察加权频数与期望加权频数之差量（N̂rc-Erc）组成的数组，HV̂（N̂）H'是Ŷ的方差的估计值，V̂（N̂）是N̂rc估计值的协方差矩阵。在SAS/STAT的SURVEYFREQ过程中，方差估计方法共有6种，即台劳级数方差估计量、复制方差估计量、自助法、平衡重复复制（BBR）法、Fay’s BBR法和刀切法［4］，因篇幅所限，此处从略。H是一个Q×P阶矩阵，其中，Q=（R-1）（C-1），P=R×C。H矩阵的元素为Ŷ的元素关于N̂的元素的偏导数。

1.3.3 广义Wald’s对数线性χ2检验统计量

对于R行C列的二维列联表资料，广义Wald’s对数线性检验基于一个（R-1）（C-1）维的数组导出，其元素Ŷrc定义如下：

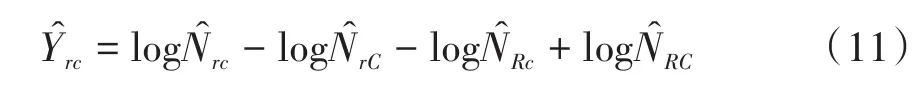
式（11）中，N̂rc是二维表中第（r，c）格上被估计的总频数。行与列变量之间的独立性假设可采用下式来表达：

式（12）中，r=1，2，…，（R-1），c=1，2，…，（C-1）。于是，广义Wald’s对数线性检验统计量的定义见下式：

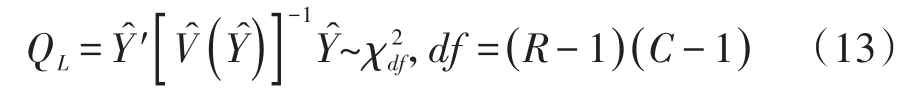
式（13）中，Ŷ是 Ŷrc的（R-1）（C-1）维的数组，V̂（Ŷ）是Ŷ的方差估计值，其计算见下式：

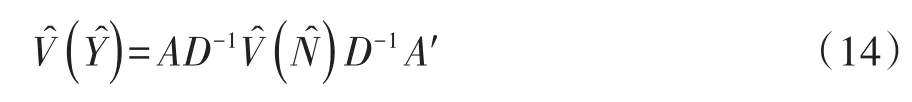
式（14）中，V̂（N̂）是估计量 N̂rc的协方差矩阵；D是一个对角矩阵，其对角线上的元素为估计的总数N̂rc；A是一个Q×P阶矩阵，其中，Q=（R-1）（C-1），P=RC×RC。

1.3.4 Wald’s F检验统计量与Wald’s校正F检验统计量

基于公式（10）得到Wald’s F检验统计量见式（15）：

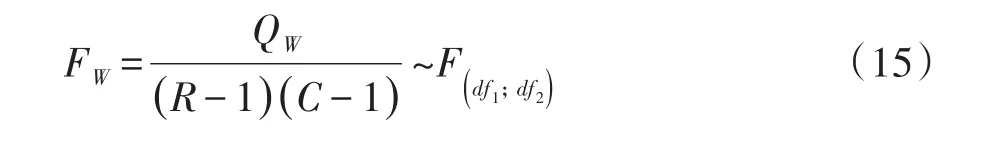
式（15）中，FW服从分子自由度df1=（R-1）（C-1）、分母自由度为df2的F分布。

对于大于2×2表的二维列联表资料，需要计算校正的F检验统计量。基于公式（10）得到Wald’s校正F检验统计量见式（16）：

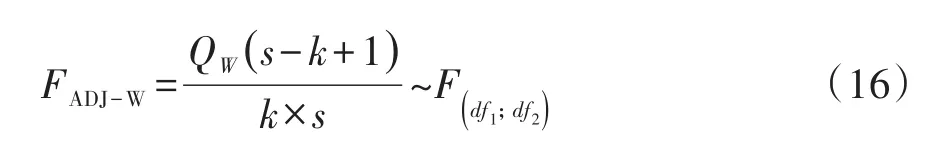
式（16）中，k=df1=（R-1）（C-1），s=df2。

上面提及的df2的取值与抽样设计和方差估计方法有关。如果采用台劳级数法估计方差，df2=群数-层数；如果没有群数，df2=观测数-层数；若不是分层设计，df2=群数-1。如果采用复制法估计方差，df2=复制数。如果采用BBR法估计方差，df2=层数。如果采用自助法和刀切法估计方差，df2=群数-层数；如果没有群数，df2=观测数-层数；若不是分层设计，df2=群数-1。

1.3.5 Wald’s对数线性F检验统计量与校正Wald’s对数线性F检验统计量

基于公式（13）得到Wald’s对数线性F检验统计量见式（17）：

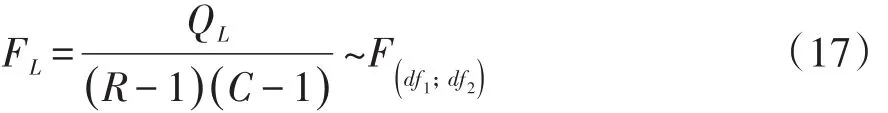
基于公式（13）得到校正Wald’s对数线性F检验统计量见式（18）：

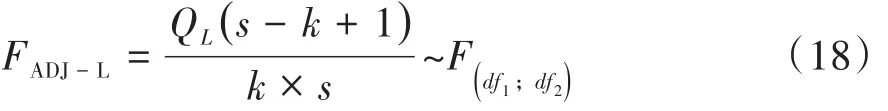
在式（17）和式（18）中，有关变量或符号的含义与式（15）和式（16）后面的解释完全相同，此处从略。

2 实例与SAS实现

2.1 问题与数据

【例1】为研究2型糖尿病患病的危险因素，某研究者随机选取某市社区常见慢性非传染性疾病的筛查中检出的2型糖尿病患者113例，同时在社区随机选取120名正常人，收集他们的相关资料，包括年龄（岁），性别（0=男性，1=女性），吸烟情况（0=不吸烟，1=吸烟），饮酒情况（0=不饮酒，1=饮酒），2型糖尿病（MD）家族史（0=无，1=有），动脉粥样硬化血栓形成（AT）家族史（0=无，1=有），收缩压（mmHg）、舒张压（mmHg）。用1和0分别表示患与未患2型糖尿病。表1列出了部分研究对象的资料［6］。试采用合适的方法分析哪些因素易导致受试对象患2型糖尿病。

表1 2型糖尿病相关危险因素的调查资料

【例2】文献［4］提供了一个关于学生信息系统（SIS）的顾客满意度调查资料。这次抽样调查的抽样设计是两阶段分层随机抽样设计。在第1阶段的各层中，根据学校的规模，采用按比例和无放回的概率抽样方式抽取学校。从每一个被抽取的学校中，随机抽取5名工作人员（包括3名教师以及2名管理者或指导者）完成SIS满意度问卷调查。SAS数据集SIS_Survey包含抽样结果和数据分析所需要的抽样设计信息。主要变量及含义如下：

Response（结果变量，即对SIS的满意程度）：很不满意、不满意、中立、满意、很满意；State（州）：乔治亚州、美国南卡罗来纳州、美国北卡罗来纳州；Newuser（用户类型）：新用户、续用用户；School（学校）：第1阶段的抽样单位；SamplingWeight（抽样权重）：基于每个抽样阶段来计算并根据是否缺失数据进行调整；SchoolType（学校类型）：高中、初中；Department（部门）：教师、管理者或指导者。其中，State（州）和Newuser（用户类型）是两个分层因素，共形成6层；School（学校）是群，共抽取了370个群。总样本含量为370×5=1850人。

基于此资料进行以下两种分析：①试分析Response（结果变量，即对SIS的满意程度）的频数分布；②试分析SchoolType（学校类型）与Response（结果变量，即对SIS的满意程度）两变量之间是否互相独立。

2.2 SAS实现

2.2.1 分析例1资料所需的SAS程序

【分析与解答】设所需要的SAS程序如下：

【程序说明】因本例中的数据很多，以文本格式存储在D盘文件夹MXWTTJXS中，数据文件名为prg35_3.dat；model语句中的选项“sle=0.5 sls=0.02”是为了演示SAS软件在逐步回归分析过程中的具体表现，即选变量进入回归方程采用的是评分检验；而从回归模型中删除自变量采用的是Wald’s检验。同时，还可以看到：检验回归模型中全部自变量的回归系数同时为0时，采用了3种检验方法，包括似然比检验、评分检验和Wald’s检验；估计回归系数的置信区间采用的是Wald’s检验。

【SAS输出结果及解释】

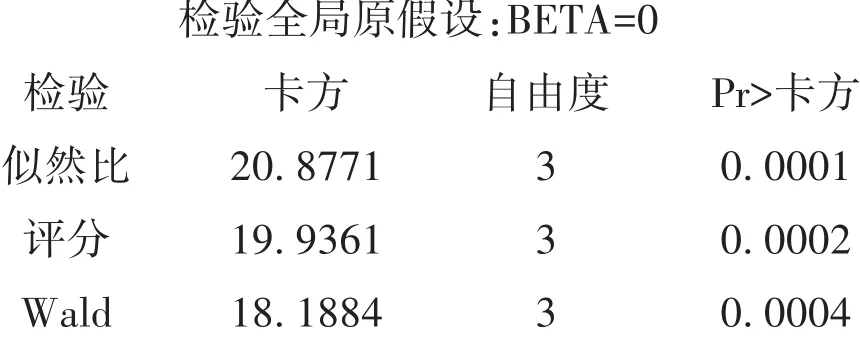
以上输出的是采用3种检验方法检验回归模型中3个回归系数同时为0的检验结果，因P值都小于0.05，说明3个自变量对因变量的影响都具有统计学意义，应该保留在回归模型中。

【说明】因篇幅所限，上面仅呈现了部分与Wald’s检验有关的输出结果，故不适合给出统计结论和专业结论。

2.2.2 分析例2资料中第1个问题所需的SAS程序

【分析与解答】设所需要的SAS程序如下：

【程序说明】tables语句中指定结果变量；strata语句中指定分层变量；cluster语句中指定群变量；weight语句中指定权重变量。第1个过程步产生单因素（这里实际上是定性的结果变量Response）频数分布表；第2个过程步是采用 Rao-Scott’s χ2检验进行拟合优度检验。

【SAS输出结果及解释】

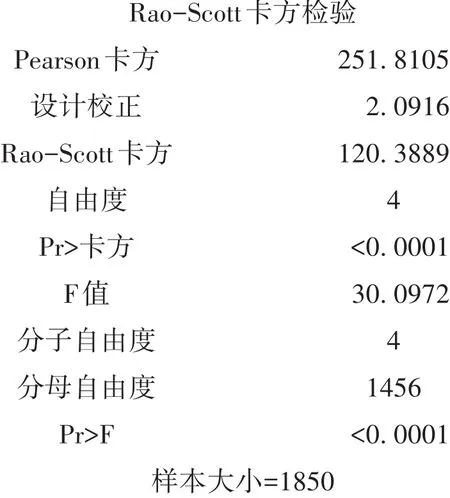
以上输出的是拟合优度检验的结果。

【统计结论与专业结论】拟合优度检验的结果为P<0.0001，说明评价结果（Response）5个档次中的频数不等，“中立”的频数最高，“很满意”的频数最低。

2.2.3 分析例2资料中第2个问题所需的SAS程序

【分析与解答】设所需要的SAS程序如下：

【SAS输出结果及解释】

以上输出的是采用 Rao-Scott’s χ2检验法对SchoolType（学校类型）与Response（结果变量，即对SIS的满意程度）两变量之间互相独立假设的检验结果。因P>0.05，说明两变量之间的独立性假设成立，即两种学校类型下评价结果的频数分布基本相同。

【说明】Rao-Scott’s χ2检验法是校正设计后的Pearson’s χ2检验法，因篇幅所限，该方法的计算公式从略，可参阅文献［4］。

【统计结论与专业结论】对学生信息系统（SIS）的评价结果不会随着学校类型的改变而改变，也就是说，各类学校给出的评价结果5种档次的频数分布与前面所呈现的“单变量频数分布”的结果（即全部被调查对象给出的评价结果）基本一致。

3 讨论与小结

3.1 讨论

Wald’s检验的应用场合比较多，不仅在广义线性回归模型的构建过程中的多个环节（例如：在检验全部回归系数是否为0、从回归模型中是否需要剔除某些自变量、求回归系数和优势比的置信区间等）上发挥了重要作用，而且在分析复杂抽样调查所得到的定性资料［7-10］方面，也起着不可或缺的作用。然而，在以下两种场合下，Wald’s检验不如似然比检验的效果好［1］：情形一，样本含量较小；情形二，回归系数的绝对值很大。

3.2 小结

本文介绍了广泛应用于定性资料统计分析的一类假设检验方法，即Wald’s检验。在定性资料和生存资料的回归分析中，常用的Wald’s检验有：一般Wald’s检验、稳健Wald’s检验和Wald’s约束χ2检验；而在复杂抽样调查定性资料的独立性检验中，常用的Wald’s检验有：广义Wald’s检验、广义Wald’s对数线性检验、Wald’s F检验、Wald’s校正F检验、Wald’s对数线性F检验和校正Wald’s对数线性F检验。本文结合两个实例并借助SAS软件，实现了前述提及的大多数检验。