如何正确运用χ2检验
——评分检验与SAS实现
胡纯严 ,胡良平 ,2*
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029*通信作者:胡良平,E-mail:lphu927@163.com)
在构建广义线性回归模型的过程中,常涉及参数的检验问题,例如:检验部分或全部回归系数是否为0,检验单个效应是否不在回归模型中以及检验平行线假定是否成立。在统计学上,实现前述检验的具体方法有评分检验、似然比检验和Wald检验。本文仅介绍评分检验及其SAS实现。
1 基本概念
1.1 评分函数
设资料由观测值 x1,x2,…,xN组成,并假定可用依赖于参数θ的概率模型f(x;θ)来描述该资料。当变量x只有有限个可能的取值代入函数f(x;θ),从而指定每一个输出的概率;当存在无穷多个输出f(x;θ)来指定概率密度函数时,对数似然函数可表示如下:

此时,评分函数[1]表示如下:

在式(2)中,“'”代表求函数的导数;若θ̂是θ的最可能值,则满足u(θ̂)=0。
1.2 评分检验统计量的定义
设θ0是θ的真值,则评分就具有均值为0、方差为i(θ0),则下式定义的检验统计量Z服从标准正态分布:

基于式(3)定义的检验被称为评分检验[1]。文献[1]还给出了Wald检验统计量,见下式:
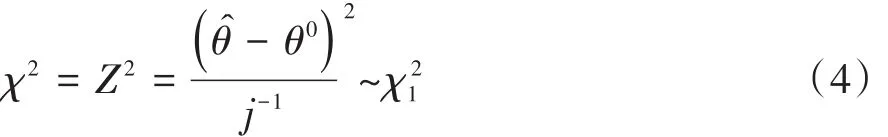
在式(4)中,θ̂是θ的最大似然估计值,θ0是θ的真值,j-1是θ的方差。
1.3 评分检验统计量的用途
在评分检验统计量中,参数θ可以是一维的,也可以是多维的(被称为参数向量)。在统计学上,经常将3种检验统计量(即评分检验统计量、似然比检验统计量和Wald检验统计量)[1-3]同时呈现出来,其主要用途如下:检验部分或全部回归系数是否为0、检验单个效应是否不在回归模型中、检验平行线假定是否成立以及检验线性假设是否成立等。
2 评分检验统计量的种类
2.1 一般评分检验统计量
设回归模型中的回归系数向量β具有K个分量,在SAS/STAT的PHREG过程中,给出的5个检验统计量(即似然比检验统计量、一般评分检验统计量、Wald’s检验统计量、稳健评分检验统计量和稳健Wald’s检验统计量)都服从自由度df=K的χ2分布。这5种检验都可以用于检验回归模型中全部回归系数是否都等于0,即H0:β=0。其中,一般评分检验统计量的定义有以下两种表达形式,见式(5)、式(6)[2-3]:
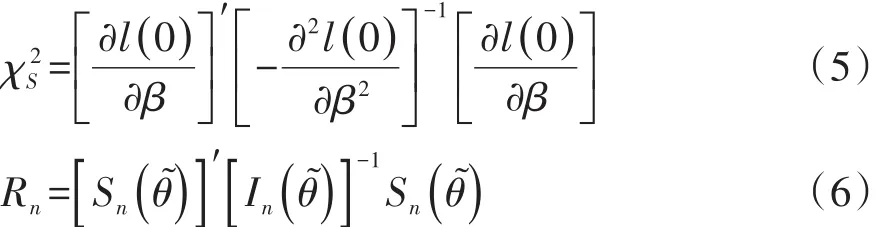
2.2 稳健评分检验统计量
在SAS/STAT的PHREG过程中,稳健评分检验统计量的定义[2]如下:
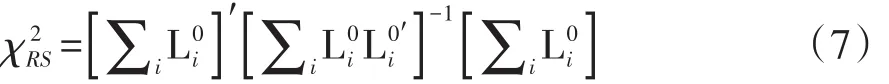
式(7)中,L0i是第i个受试者在β=0处的评分残差;也就是说,L0i=Li(0,∞),得分过程L(iβ,t)的定义如下:

向量L̂i≡Li(β̂,∞)是第i个受试者的得分残差。
【说明】在SAS/STAT的PHREG过程中,介绍了4种残差,分别是边际残差、偏差残差、Schoenfeld残差和得分残差。上式中涉及其他一些变量或符号,参见文献[2],此处从略。
2.3 残差评分检验统计量
2.3.1 检验部分或全部回归系数是否为0
在累积和广义(或扩展)的logistic回归模型中,假定因变量有K(i=1,2,…,K)个类别,共同的自变量有S个。也就是说,在每一类中拟合logistic回归模型时,都涉及一个截距项和S个自变量(注:指尚未筛选掉某些自变量)。为了检验部分回归系数是否为0,可以采用残差评分χ2检验。
让g(β)代表对数似然函数关于参数向量β的一阶偏导数向量;让H(β)代表对数似然函数关于参数向量β的二阶偏导数矩阵。也就是说,g(β)是梯度向量,而H(β)是哈森矩阵。让I(β)代表“-H(β)”的期望。考虑一个无效假设H0,让β̂H0是无效假设条件下β的最大似然估计值(MLE)。在SAS/STAT的LOGISTIC过程中,残差评分检验统计量的定义如下:

式(9)中的χ2RS渐近服从自由度为df的χ2分布。其中,参数向量β、无效假设H0与H0对应的向量β和自由度df都会随着因变量的具体情形不同而有所变化。具体地说,有以下两种情形。
情形一:累积反应变量模型或称多值有序因变量模型。
参数向量β=(α1,α2,…,αK,β1,β2,…,βS)';无效假设 H0:βt+1=βt+2=…=βS,t 情形二:广义反应变量模型或称多值名义因变量模型(当K=2时为二值反应变量)。 参数向量 β =(α1,α2,…,αK,β'1,β'2,…,β'S)';其中,β'i=(βi1,βi2,…,βiS);i=1,2,…,K;无效假设 H0:βi,t+1=βi,t+2=…=βi,S,t 2.3.2 检验单个效应是否不在回归模型中 解决问题的基本思路:假定有两组自变量,A组中有S个自变量(可构建一个全模型);B组中有S-1个自变量(可构建一个简化模型);B组中的全部自变量都包含在A组中。将A组比B组多出来的一个自变量记为xt[t∈(1,2,…,S)],于是,将A组与B组自变量及其资料分别代入式(4)计算,便可得到两个χ2值,它们具有不同的自由度。求出这两个χ2值之差,再基于它们的自由度之差,就可依据χ2分布求出尾端概率。 自由度的确定方法:若是多值有序因变量,全模型与简化模型的自由度之差等于1;若是多值名义因变量,全模型与简化模型的自由度之差等于K(当K=2时为二值因变量的情形)。当检验结果为P<0.05,表明不在B组中的自变量xt[t∈(1,2,…,S)]具有统计学意义;反之亦然。 2.3.3 检验平行线假定是否成立 设因变量Y为多值有序的且水平数为K+1(即水平数大于2),让因变量Y的取值分别为1,2,…,K,K+1。假定有S个自变量,在没有平行线假设的条件下,一般的累积logistic回归模型可用下式表达: 在 式(10)中 ,g(·)是 连 接 函 数 ;βi=(αi,βi1,βi2,…,βiS)'是Y=i条件下的一个未知参数向量,它的分量分别是一个截距、S个斜率。这个一般累积模型的参数向量可表示成:β=(β'1,β'2,…,β'K)',它是由K个分量组成的一个向量,而每个分量就是前面所呈现的向量[即βi=(αi,βi1,βi2,…,βiS)']。 给定平行线的无效假设:H0:β1m=β2m=…=βKm,1≤m≤S。回归系数β有两个下标,第1个下标代表因变量Y的取值或水平代码,第2个下标代表自变量的顺序编号。若用语言描述上述无效假设H0,即在因变量Y的K个水平条件下的K个logistic回归模型中编号相同的自变量具有相等的回归系数。也就是说,K个logistic回归模型仅截距不同,自变量线性组合中只有一组共同的回归系数。 用统计学语言表述如下:让 β1,β2,…,βS代表共同斜率系数,让 α̂1,α̂2,…,α̂K和 β̂1,β̂2,…,β̂S分别代表截距参数与斜率参数的最大似然估计值。那么,在H0成立的条件下,β的最大似然估计见式(11): 此时,与无效假设H0对应的残差评分χ2检验统计量见式(12): 【说明】对平行线假定的检验可视为对参数有线性约束的检验(简称约束检验[6])的特例,后者常被冠以拉格朗日乘数检验(参见下文)。 让β͂为在限制条件L'β=0下从广义估计方程中求解得到的回归参数;让 S(β͂)为在 β͂时广义估计方程的值。Boos和Rotnitzky与Jewell描述了在广义估计方程中将评分检验应用于检验L'β=0,其中L'是用户指定的r×p阶比较矩阵。于是,广义评分检验统计量[2]见下式: 在式(13)中,∑m是基于模型的协方差估计值,∑m是经验协方差估计值,T服从自由度df=r的χ2分布。 在SAS/STAT的GENMOD过程中的定义如下:当用户给回归模型中的参数施加某些限制(例如:NOINT,即强制性要求截距为0;又例如:NOSCALE,即强制性要求某些定量随机变量的概率分布中的尺度参数取固定值)时,需要有相应的检验方法来评价这些限制的有效性。这个检验方法被称为拉格朗日乘数检验或约束评分检验。检验统计量[2]见式(14): 式(14)中,S是在与被限制参数对应的限制的最大值点上估计的评分向量的成分;而V=I11-I12I-122I21,其中矩阵I是信息矩阵,下标中的1指被限制的参数,下标中的2指未被限制的其他参数。 【说明】因篇幅所限,在SAS/ETS的ENTROPY过程中的定义、在SAS/ETS的MDC、MODEL和QLIM过程中的定义以及在SAS/ETS的PANEL过程中的定义从略。 【例1】一项关于成年人心理健康问题的研究,调查了某城市40例成年居民的心理健康状况(1=无心理问题,2=存在轻微症状,3=存在中度症状,4=存在精神损害),考察的两个原因变量分别是社会经济地位(0=低,1=高)和生活事件评分,资料见表1[4]。试分析心理健康状况与两个原因变量的关系。 表1 成年人心理健康状况调查资料 【例2】随机纳入30例在某医院就诊的仅有胸闷症状的非器质性心脏病患者,收集患者在24小时中的早搏数(y),试问早搏是否与吸烟(x1)、性别(x2)和喝咖啡(x3)有关。资料见表2[5]。 表2 某医院伴有胸闷症状的非器质性心脏病患者情况 3.2.1 对例1的分析与解答 【分析与解答】设所需要的SAS程序如下: 【SAS输出结果及解释】 第1个过程步的主要输出结果: 以上是模型中含有截距项和自变量life时的比例优比假设的评分检验结果,也被称为平行线假设检验结果。因χ2RS=0.8865,df=2,P=0.6419,说明资料满足构建logistic回归模型的前提条件。 以上是采用3种检验方法检验此时的logistic回归模型(含截距项和一个自变量life)是否成立,由于3种检验结果均有P<0.05,说明此时的logistic回归模型成立。 以上是逐步选择汇总,从第2列与倒数第3列可知,选择自变量进入回归模型时采用的是评分χ2检验;而从第3列与倒数第2列可知,删除自变量时采用的是 Wald χ2检验。 第2个过程步的主要输出结果: 以上输出的是平行线假定的检验结果,因P=0.6761>0.05,说明资料满足构建logistic回归模型的前提条件。 以上是采用3种检验方法检验此时的logistic回归模型[含截距项和两个自变量(life和society)]是否成立,由于3种检验结果均有P<0.05,说明此时的logistic回归模型成立。 以上输出的是线性假设检验结果。第1行的结果说明0.5×β1+1×β2=0的假设成立;第2行的结果说明 β1=β2的假设不成立。这里采用的是 Wald χ2检验,而不是似然比χ2检验和拉格朗日χ2检验。 【说明】为节省篇幅,以上仅呈现了与评分检验有关的输出结果,故不适合给出统计结论与专业结论。 3.2.2 对例2的分析与解答 【分析与解答】设所需要的SAS程序如下: 【SAS输出结果及解释】 第1个过程步的主要输出结果: 以上输出的是拉格朗日乘数检验结果,χ2LM=8.6315,P=0.0017,说明资料存在过度离散现象,不适合直接拟合Poisson分布回归模型。 第2个过程步的主要输出结果: 以上输出的是拉格朗日乘数检验结果,χ2LM=0.9727,P=0.1620,说明此时的资料(不包括自变量x3)不存在过度离散现象,可直接拟合Poisson分布回归模型。 第3个过程步的输出结果与评分检验无关,为节省篇幅,此处从略。 【说明】为节省篇幅,以上仅呈现了与评分检验有关的输出结果,故不适合给出统计结论与专业结论。 在进行广义线性模型[6]分析,特别是进行多重logistic回归模型[7-10]分析时,在多个环节上需要对参数进行假设检验,有时还需要在参数处于特定约束条件下对其进行检验。通常涉及3种检验,即评分检验、似然比检验和Wald检验;当有约束条件时,其检验被称为约束检验[6]或拉格朗日乘数检验[2],但它们也被称为评分检验[2]。当在某种场合下同时应用以上提及的多种检验方法时,检验结果可能不尽相同,但通常情况下不会出现截然相反的结果。事实上,在上述提及的几种检验统计量的推导过程中,一般都基于大样本条件下给出渐近的结果,而不是精确计算的结果。 本文介绍了与评分检验有关的基本概念,介绍了5种评分检验统计量,即一般评分检验统计量、稳健评分检验统计量、残差评分检验统计量、广义评分检验统计量和拉格朗日乘数(或约束评分)检验统计量。在介绍残差评分检验统计量这部分内容时,详细呈现了在构建广义线性模型过程中的3种适用场合;在介绍拉格朗日乘数(或约束评分)检验统计量这部分内容时,详细呈现了此种检验统计量的多种不同定义形式,该检验主要用于对参数有线性约束的场合。最后,基于两个实例并借助SAS软件,说明了评分检验的常用场合和呈现形式。
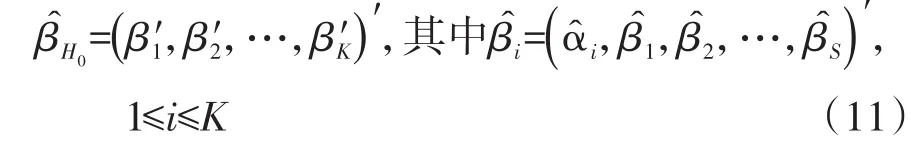

2.4 广义评分检验统计量
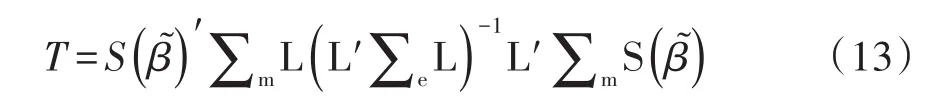
2.5 拉格朗日乘数(或约束评分)检验统计量

3 实例与SAS实现
3.1 问题与数据


3.2 分析与解答












4 讨论与小结
4.1 讨论
4.2 小结

