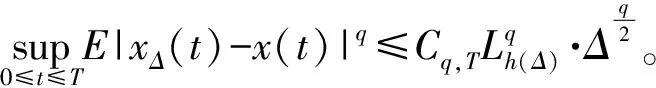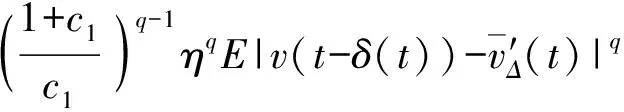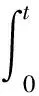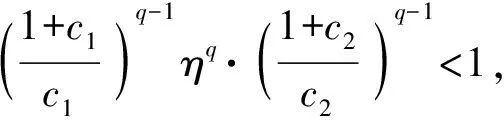中立型变时滞随机微分方程数值解的强收敛性
王 歌 兰光强
(北京化工大学 数理学院,北京 100029)
引 言
中立型时滞随机微分方程是描述诸如医学、生态学、经济学、物理学等学科中众多现象的一种重要工具。然而,由于此类方程的复杂性,虽然其应用广泛,但是解析解却很难得到,因此研究其数值解以及数值解的收敛性很有必要。另一方面,过程的当前状态依赖于其过去的状态,但是这种依赖未必是常时滞的,从而使得考虑变时滞情形具有重要的实际意义。Mao等[1-2]提出截断Euler-Maruyama(EM)方法,并对该方法得到的数值解的收敛性和稳定性进行了研究。Miloševi[3]和Guo等[4]分别研究了时滞随机微分方程和中立型时滞随机微分方程数值解的收敛性。Lan等[5-7]提出了修正截断EM方法,并且得到典型随机微分方程和中立型常时滞随机微分方程的数值解的收敛速度和渐进稳定性。由于在变时滞情形下通常的修正截断方法会变为隐式格式,而相比于显式格式隐式格式通常计算量较大,因此本文将研究对应方程的显式格式(改进的修正截断EM方法)的收敛性及收敛速度。
1 基本假设、定义及重要引理
设(Ω,F,{Ft}t≥0,P)是一个完备的概率空间,考虑中立型变时滞随机微分方程为
d[x(t)-u(x(t-δ(t)))]=f(x(t),x(t-δ(t)))dt+g(x(t),x(t-δ(t)))dB(t)
(1)
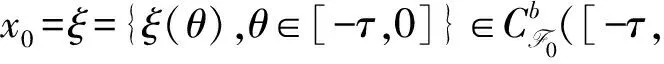

H2存在常数η∈(0,1),对∀x,y∈Rn,都有|u(x)-u(y)|≤η|x-y|,当u(0)=0时,|u(x)|≤η|x|。
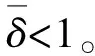
H4(Khasminskii-type条件) 存在常数p≥2和K>0,使得对于∀x,y∈Rn,a∈(0,1],有
|x|2+|y|2)
H5存在常数Cξ,对于p≥2有
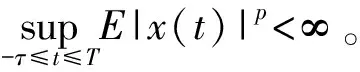
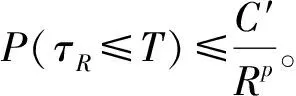
令Δ∈(0,1)为步长且τ=mΔ,对于充分小的Δ*>0,令h(Δ)是正的严格递减函数h:(0,Δ*]→(0,∞)且满足
(2)
由文献[6]知若给定LR,则函数h一定存在。
对任意的Δ>0,定义修正截断函数fΔ为
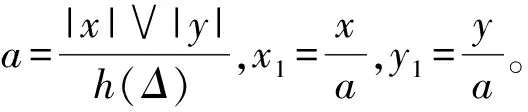
下面定义改进的修正截断EM格式。令tk=kΔ,N=T/Δ,Xk=ξ(tk),-m≤k≤0,X-m-1:=X-m,若k=0,1,…,N,令
Xk+1=u(Xk-Ik)+Xk-u(Xk-1-Ik-1)+fΔ(Xk,Xk-Ik)Δ+gΔ(Xk,Xk-Ik)ΔBk
(3)

为定义连续格式,令
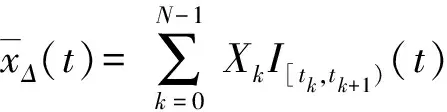
(4)
(5)
(6)
(7)
定义xΔ(t)=ξ(t),t∈[-τ,0],对∀t∈[0,T],令
(8)
对∀t∈[tk,tk+1),上述格式也可写成如下形式
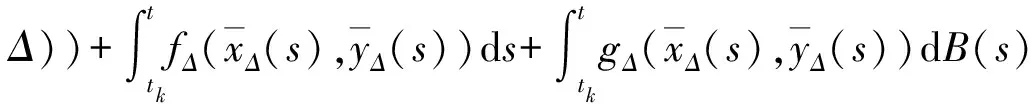
(9)

引理1假设H1成立,那么对于任意固定的Δ>0,有
证明参见文献[7]中引理3.1。
引理2假设H4成立,则有

证明参见文献[7]中引理3.2。
引理3对于∀t≥0,有
证明不妨设t∈[tk,tk+1),由式(6)、(7)可知
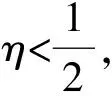
证明由式(9)易知,
又由式(6)、(7)可知
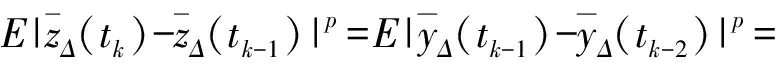
根据[x]的定义和假设H3可知
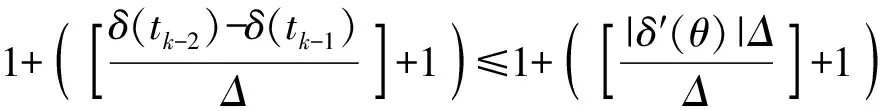
故
又由引理1,所以得到
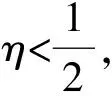
引理5设引理4中的条件均成立,则
证明不妨设t∈[tk,tk+1)。由式(9)得
注意到
从而由引理4得
根据引理5不难得到
引理6假设H1~H5均成立,则
证明由伊藤公式得
下面分别估计I1、I2、I3、I4这4项。
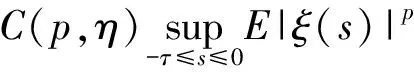
(10)
由引理2和Young不等式得
(11)
由引理1和Young不等式得
(12)
同理,由引理5和Young不等式可得
(13)
由式(10)~(13)得
再根据Gronwall引理[8]即可得证。
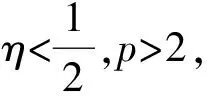

证明
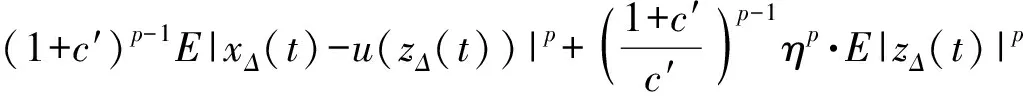
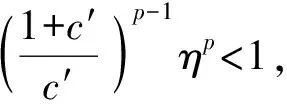
(14)
显然将式(14)中的xΔ(t)换成xΔ(t∧ρΔ,R)不等式仍成立。

引理8假设引理7中的假设均成立,则对∀t∈[tk,tk+1)和充分小的Δ(<1),2 证明显然t-δ(t)∈[tk-1-IkΔ,tk+1-Ik+1·Δ),由H3,可得 tk+1-Ik+1Δ-(tk-1-IkΔ)=2Δ+(IkΔ-Ik+1Δ)≤3Δ+[|δ′(θ)|]Δ=3Δ 由引理7,结论得证。 证明截断函数定义为FR(x,y)=fh-1(R)(x,y)和GR(x,y)=gh-1(R)(x,y),取Δ充分小,易知对任意|x|∨|y|≤R≤h(Δ),FR(x,y)=fh-1(R)(x,y)=f(x,y)=fΔ(x,y),同理GR(x,y)=gh-1(R)(x,y)=g(x,y)=gΔ(x,y)。 设v(θ)=ξ(θ),θ∈[-τ,0],当t≥0时考虑如下中立型变时滞随机微分方程。 d[v(t)-u(v(t-δ(t)))]=FR(v(t),v(t-δ(t)))dt+GR(v(t),v(t-δ(t)))dB(t) (15) 对任意固定的R,FR、GR满足全局Lipschtiz条件,故方程(15)有唯一的解v(t),t≥-τ,所以有 P(x(t∧τR)=v(t∧τR),∀t∈[0,T])=1 (16) 由解的唯一性,方程(1)、(15)对应的数值解满足 P(xΔ(t∧ρΔ,R)=vΔ(t∧ρΔ,R),∀t∈[0,T])=1 (17) 令l(t)=v(t)-u(v(t-δ(t))),lΔ(t)=vΔ(t)-u(v′Δ(t)),则 根据引理5和引理8得 (18) 同理可得 (19) 易知将t替换成t∧θΔ,R,其中θΔ,R=τR∧θΔ,R,式(19)仍成立。类似于文献[6]中引理4.1的证明,由Gronwall引理得 其中, 由式(16)、(17)以及停时的定义可得 再由标准的截断程序[1,5]和引理7即得
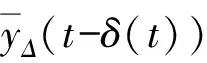

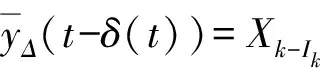
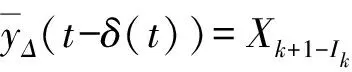
2 主要结果与证明