考虑螺栓连接的航空发动机管路建模及振动特性分析
刘中华 ,李建福 ,孙志航 ,柴清东 ,马 辉 ,贾 铎
(1.空装驻沈阳地区第二军事代表室,沈阳 110043;2.东北大学机械工程与自动化学院,沈阳 110819;3.中国航发沈阳发动机研究所,沈阳 110015)
0 引言
针对航空发动机外部管路采用卡箍支撑的结构特点,尹泽勇等[4]对卡箍刚度进行了有限元计算,并通过试验对典型卡箍的刚度进行了验证,获得了卡箍刚度的计算方法,可用于工程实际;Ulanov等[5]通过迟滞回线确定了卡箍刚度及等效黏性阻尼,提出一种基于ANSYS 的振动特性分析方法,且仿真计算与试验结果吻合较好;Nassar 等[6]通过试验分析了拧紧速度等因素对螺栓连接性能的影响,提高了估算其夹紧力的可靠性;李占营等[7]对柔性卡箍的实际结构进行分析,得出卡箍横向刚度具有分段线性的特点,并进一步分析了其对振动响应的影响;Qiu 等[8]基于有限元法分析了影响螺栓连接性能的各项参数,表明预紧力是最为主要的参数;Gao 等[9]采用梁单元模拟管路,用弹簧模拟卡箍的形式建立卡箍管路系统模型,并通过试验验证了模型的有效性;Rao 等[10]基于有限元提出反推螺栓预紧力的算法,获得了螺栓不松动的预紧力范围;Kim 等[11]采用有限元软件通过不同的建模方法建立了带有螺栓连接的结构,表明采用实体螺栓模型的计算结果最为准确。
由以上的文献分析可知,针对管路-卡箍系统的力学模型,大多将卡箍螺栓的拧紧影响等效为卡箍本身的刚度特性,与实际结构存在一定的差距。本文在已有研究基础上,考虑管路-卡箍系统模型中螺栓拧紧的影响,采用有限元接触模型与试验相结合的方式进行对比研究。
1 有限元模型建立
1.1 实体模型建立
考虑管路-卡箍系统的实际结构,基于ANSYS有限元软件,建立了管路卡箍支撑条件下的实体接触有限元模型,如图1所示。
其中管路外径8 mm,内径6.4 mm,长500 mm,卡箍跨距450 mm 且对称分布。相应管路、卡箍及其他构件的材料参数[12]见表1。

表1 管路及卡箍材料参数
管体、金属橡胶及卡箍板材均选用Solid45 实体单元进行网格划分,共46690 个节点,43156 个单元。金属橡胶与箍带间采用共节点操作,模拟真实焊接结构;金属橡胶与管路间为标准接触,其中金属橡胶面为接触面,管路面为目标面,接触单元与目标单元分别选用Conta174 和Targe170 单元;卡箍螺栓部分采用Beam188 梁单元建模,每个螺栓划分为4 个单元,5 个节点,在螺栓中心节点添加Prets179 预紧力单元,模拟卡箍螺栓的预紧效果;螺栓头部与螺栓台采用刚性区域模拟,即螺栓头部与箍带相接触的区域的所有节点采用刚性区绑定在一起;考虑到拧紧后上下箍带的实际接触长度,对上箍带边缘3 个节点的位移约束为0,达到固定约束的目的。
1.2 管路弹性模量优化
通过对管路的测量,其结构参数误差较小,而由于自购管路其弹性模量可能存在一定的偏差,为了消除管路自身的误差,更好地反映卡箍对管路的动力学特性所造成的影响,提高螺栓拧紧对管路动力学影响的分析精度,需对管路弹性模量通过自由模态试验进行修正。采用1 阶优化算法对最佳弹性模量进行寻优,优化范围为1.8×1011~2.4×1011Pa,迭代次数50次,初值为2.04×1011Pa。优化后的弹性模量结果为1.99×1011Pa,其中前8阶固有频率对比结果见表2。
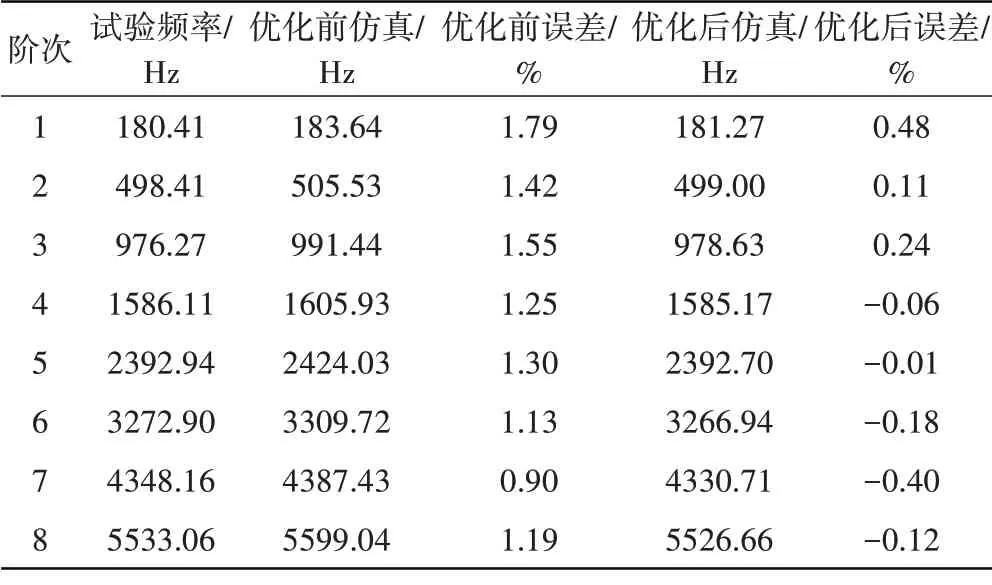
表2 试验与优化结果对比
2 模型验证
2.1 模态试验验证
采用上文修正后的管路模型,考虑卡箍螺栓的预紧力效应对管路固有特性的影响,在拧紧力矩为7 N·m下对固有频率进行仿真计算,采用如下经验公式[13]。
(1)计算预紧力。
高校学历继续教育人才培养质量观主要有两种:一种是学员学科知识理论扎实、专业基础牢固,另一种是学员实践能力强、综合素质高。如大众化以后的高校教育面临的变化首先就是学历继续教育学员的专业水平比过去低,且参差不齐,社会却对学员素质呈现出多元化和多层次要求,按专业目标与规格培养的规模化人才忽视学生和成人学员的个体差异,不利于学员的发展。所以高校学历继续教育人才培养应定位为大众教育,树立以学员实践能力与综合素质提升为主的教育质量观[1]。

式中:T为拧紧力矩;d为螺栓直径,本文d=6 mm。
由于预紧力的存在,在ANSYS 软件模态求解前应进行静力学分析以考虑预应力影响。
为证明仿真模型有效性,通过锤击法获得管路系统固有频率及振型[14],试验测试现场如图2 所示。采用DH5956测试系统进行数据采集和分析。

图2 锤击试验
仿真计算与试验测试对比结果见表3。从表中可见,在拧紧力矩为7 N·m 时,管路各方向仿真计算的前2 阶固有频率与试验结果基本一致,误差均在4%以内,能够满足实际工程需要。其中管路x方向固有频率低于管路y方向的,这是因为金属橡胶卡箍y方向是螺栓预紧的方向,而在x方向管路靠卡箍结构形状夹紧,所以管路x方向固有频率低于管路y方向的。这也体现出卡箍不同方向刚度不一致的特点。

表3 固有频率仿真与试验结果对比
管路y向试验及仿真前2 阶振型对比如图3 所示;x向振型与之类似,不再赘述。

图3 振型对比
2.2 基础激励试验验证
航空发动机管路经常受到旋转机械产生的周期性不平衡激励作用,当激振频率接近管路的固有频率时,往往导致管路产生大幅度共振。卡箍管路系统在基础激励下的振动测试系统如图6 所示。电磁振动台用于模拟机匣的基础激励,激振加速度为0.5g。
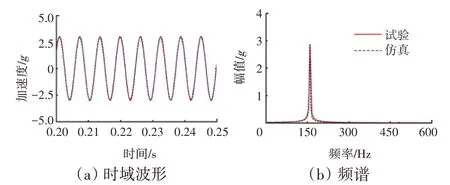
图4 仿真与试验振动响应对比
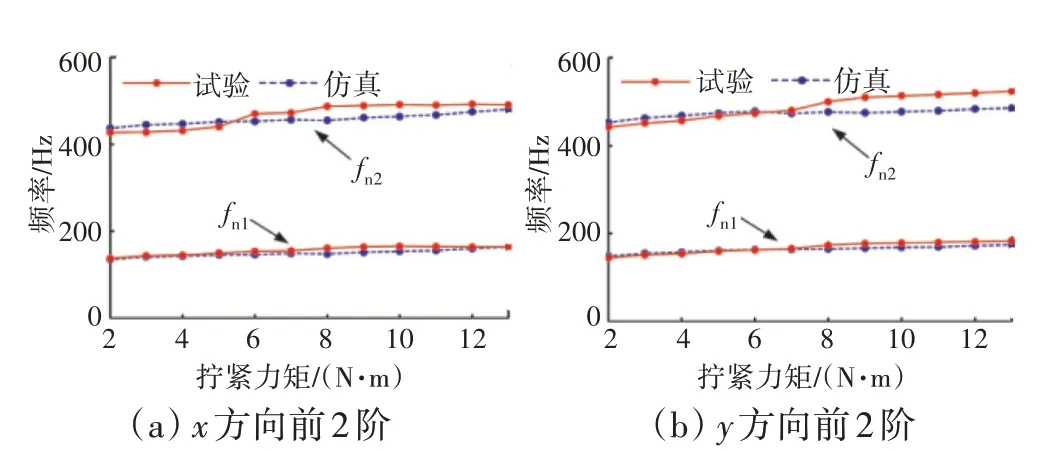
图5 仿真与试验固有频率对比

图6 不同跨距下频响函数
在响应计算中选取比例阻尼进行求解,模态阻尼比均为0.04,仿真计算与试验测试的对比结果如图4所示。二者吻合较好,充分验证了本文模型的有效性。
3 固有特性参数分析
3.1 拧紧力矩对管路固有频率的影响
航空发动机外部管路在机匣外装配过程中,卡箍上的螺栓通过人工手动拧紧,拧紧力矩存在差异。仿真模型选用上文修正后的有限元模型,在螺栓上施加不同拧紧力矩,分析管路卡箍螺栓在拧紧力矩为2~13 N·m 下的固有频率。仿真计算与试验测试对比结果如图5所示。
从图5 中可见,随着拧紧力矩的不断增大,管路的固有频率逐渐升高,这是由于随着螺栓的拧紧,金属橡胶逐渐被挤压,支承刚度逐渐增大,使管路固有频率不断提高。在不同拧紧力矩下,管路不同方向第1、2 阶固有频率最大误差均在8%以内,满足实际工程需求。此外,在拧紧力矩达到8 N·m 以上时,管路的固有频率提高缓慢且趋于稳定,这是因为金属橡胶已经被压实,支承刚度增大有限。
3.2 卡箍跨距对管路固有频率的影响[15]
卡箍在航空管路的布局中起着固定约束的作用,但由于发动机装配空间问题,许多管路的固定卡箍跨距均不相同。采用与前文相同的管路模型,通过固定管路一端卡箍,调整另外一端卡箍位置,分析管路在不同卡箍跨距下,管路系统在2000 Hz 以内的固有频率,并通过试验验证仿真计算的准确性。在不同跨距下试验的频响函数如图6 所示,仿真计算与试验测试的对比结果见表4。从图6 和表4 中可见,在不同卡箍跨距下,固有频率均吻合较好,最大误差未超过6.06%。一方面,说明卡箍模型的准确性,相应的卡箍模型可应用于工程实际;另一方面,根据计算结果,在固定一端卡箍时且保证管长不变的情况下,增加卡箍跨距将使管路基频呈现先提高后降低的趋势,这是由于管路在小跨距时,一端悬臂,随着跨距的增大,管路悬臂端逐渐减小,因此呈现此趋势。
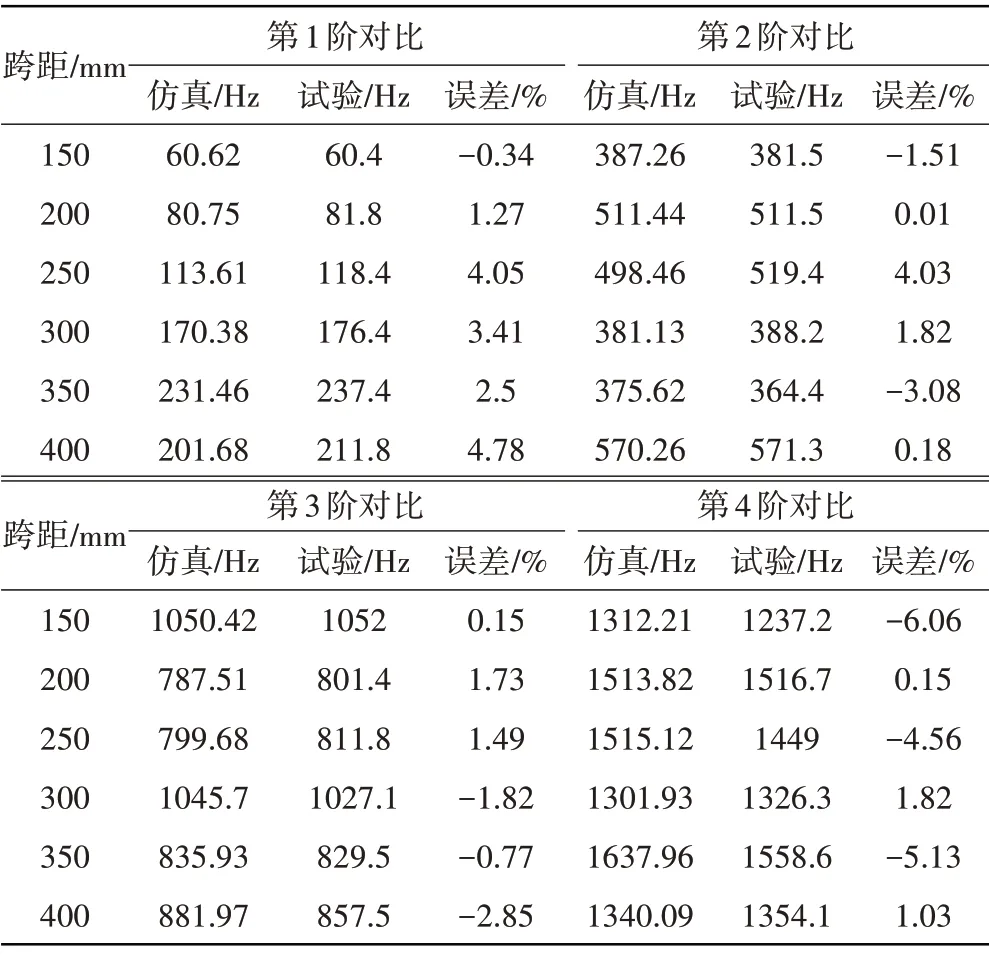
表4 不同跨距下管路固有频率
3.3 拧紧力矩对不同管长固有特性的影响
在实际管路布局安装时,通常管路长度、跨度及拧紧力矩会有所不同。研究长0.2、0.4、0.6 m 的管路在拧紧力矩为2~13 N·m 下的固有频率变化规律。在建模过程中,卡箍中心距离管路两端均为0.025 m,其余参数参考前文的有限元模型。
仿真计算结果如图7 所示。对于不同的管长,管路y方向固有频率均大于x方向的,这与前文的原因相同。从图中可见,当管长为0.2 m时,随着拧紧力矩的增大,管路y方向第1阶固有频率提高了205 Hz;而当管长为0.6 m 时,随着拧紧力矩的增大,管路y 方向第1 阶固有频率仅提高20 Hz。即随着管路长度的增加,固有频率受拧紧力矩的影响逐渐减小,也即卡箍的支承刚度对管路固有频率的影响逐渐减小。这是因为随着管路长度的增加,管路的结构刚度对固有频率的影响逐渐增大,而支承刚度的影响逐渐减弱。
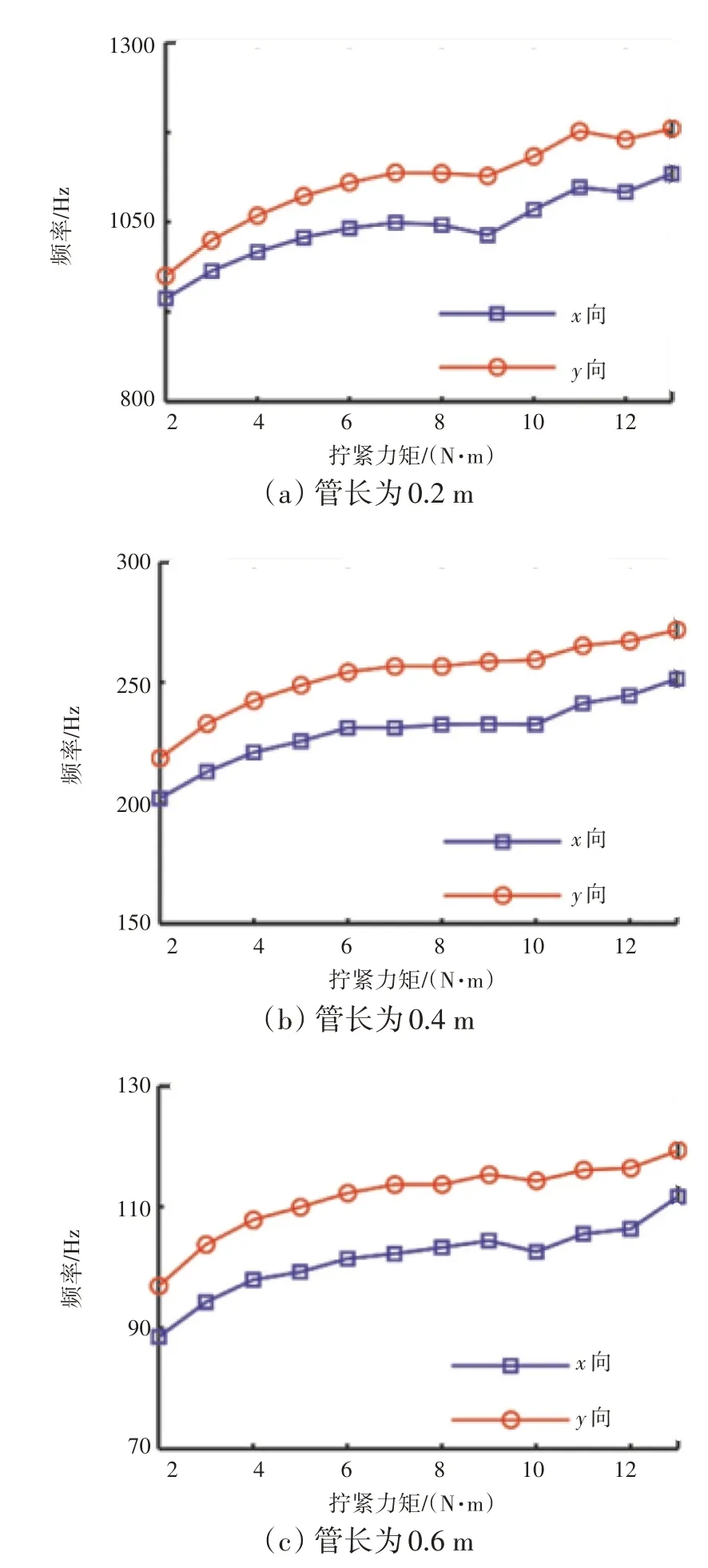
图7 拧紧力矩对不同长度管路固有特性影响
4 结论
(1)针对双卡箍夹持管路系统,基于ANSYS软件建立了考虑螺栓连接的管路系统有限元模型,利用锤击试验和基础激励响应试验进行验证,结果充分表明本文模型的有效性。
(2)由于卡箍自身结构的不对称性,卡箍刚度也具有不对称的特点,螺栓预紧方向的刚度大于另一方向的,通过试验与仿真计算的验证。
(3)通过试验及仿真对比可知,随着拧紧力矩的增大,管路的固有频率呈提高趋势,对于本文的研究对象而言,在拧紧力矩达到8 N·m 以后,管路固有频率趋于稳定。
(4)拧紧力矩对不同长度管路固有特性的作用不同,管路越长,拧紧力矩的作用越弱,即卡箍的支承刚度对管路固有频率的影响越弱。

