基于无迹粒子滤波算法的航空发动机排气温度预测

余 臻 ，刘 洋 ，魏 芳 ，刘利军 ，

（1.厦门大学航空航天学院，福建厦门 361005；2.中国航发商用航空发动机有限责任公司，上海 200241；3.中国船舶航海保障技术重点实验室，天津 300450）

0 引言

航空发动机的工作环境恶劣，多为高温、高腐蚀、高转速条件，其安全工作寿命难以准确得知[1]。发动机性能指标包括排气温度裕度（Exhaust Gas Temperature Margin，EGTM）、高压压气机转子角速度偏差量（Delta N2，DN2）、平均滑油消耗率（Average Oil Consumption，AOC）等，其中EGTM 是最重要的指标之一，是发动机在海平面压力、拐点温度条件下全功率起飞时，排气温度与标准规定的排气温度红线值之间的差值。随着发动机飞行循环数的增加，发动机各零部件磨损老化程度增加，排气温度持续升高，使得EGTM值逐渐降低，达到标准规定的EGTM阈值。

在20世纪90年代初建立的基于发动机性能参数的性能衰退失效分析方法，为高可靠性设备的可靠性分析提供了新的分析方法。Gertsbackh 等[2]率先提出基于性能退化数据的设备可靠性模型的预测方法；Nelson[3]发现发动机部件的失效特性会在发动机衰退信息中有所体现，这些信息能具体反映出零部件的衰退状态；Meeker 等[4]利用退化失效模型解决了传统可靠性理论无法很好处理的一些实际问题；Wu 等[5]基于数据驱动的退化量统计模型，采用模糊聚类方法研究了零部件退化失效分布。随着发动机制造技术的进步，发动机可靠度提高，发动机失效数据大大减少，使得样本数量减少。Erto[6]利用发动机零部件常见的先验信息，分别对经典的概率分布模型进行分析，对参数进行了估计；Cox[7]给出了针对单系统的剩余寿命分布的混合估计方法；王鑫等[8]提出了LSTM 预测模型参数优选算法，提高了对故障时间序列预测的准确度；张营等[9]在过程神经网络的基础上提出了优化算法，结合混沌粒子群算法对发动机的排气温度进行预测，获得较高的预测精度。

发动机的性能衰退主要表现为其性能衰退参数值呈非线性减小趋势[10-11]，可采用能够处理非线性时间序列的方法进行预测。

本文提出了一种基于粒子滤波[12-14]（Particle Filter，PF）的航空发动机剩余大修寿命预测方法。提出的无迹粒子滤波（Unscented Particle Filter，UPF）算法首次应用在航空发动机EGTM 预测领域，UPF 以无迹卡尔曼滤波（Unscented Kalman Filter，UKF）的结果作为建议分布[15]，引入最新观测值进行预测修正。

1 无迹粒子滤波算法

粒子滤波基于蒙特卡罗和递归贝叶斯滤波方法[16]。为了解决粒子权重差异大的问题，有2 种策略，即重采样和选择合理的建议分布[17]。重采样会导致粒子贫化，选择合理的建议分布是解决退化问题的较优选择。

粒子滤波是由表示未知状态空间的采样值的1组粒子的近似。目前，粒子滤波已经成为了解决非线性、非高斯系统参数估计和状态滤波问题的主流方法。

1.1 粒子滤波框架

对于航空发动机EGTM 预测，可以用如下的数学状态空间方程来表示。

系统状态方程

系统观测方程

式中：xt∈Rn，为系统的状态变量；yt∈Rnz，为系统在t时刻的测量值；ft为通过上一时刻的状态值预测下一时刻状态值的函数；ht为通过当前时刻状态值预测输出值的函数；mt、nt分别为系统的过程噪声和观测噪声，二者之间相互独立。

贝叶斯滤波包含预测和更新2 部分。预测部分是利用系统的状态方程，在系统测量值未知的前提下，预测状态的先验概率密度

而更新部分则是在已经得到最新的观测值yt的条件下，对先验的概率分布进行修正，得到xt的后验概率

对于一般高阶非线性、非高斯过程，式（4）难以求解。所以粒子滤波采用蒙特卡洛采样来避免积分难的问题。利用一系列从已知分布采样的粒子来估计后验概率

式中：δ()为狄拉克函数；N为粒子个数；i为粒子序号。在得到后验概率后，当前时刻的后验期望值为。

然而，因为无法获知真实的状态后验概率，所以如果需要通过后验概率来获取粒子分布，则需要从1个已知分布q(x|y)中采样得到粒子

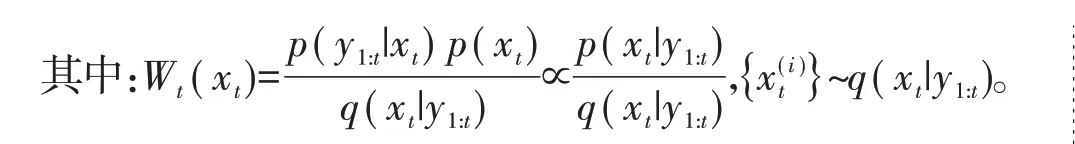
上述粒子权重的计算采用直接计算方式，每进行1 次迭代就需要重新计算，效率低。所以需要重新对权重公式进行递推

至此描述了完整的粒子滤波算法。从上述算法得知，建议分布q(xt|y1:t)的选取对于算法的效果非常重要。上述涉及到建议分布的内容主要包含2 部分：一部分是粒子是从建议分布中选取的，另一部分是粒子的权重计算需要用到建议分布。同时可知，当建议分布选取为系统先验分布p(xt|xt-1)时，权重的计算复杂度会大幅降低，即为

这极大地促进了粒子滤波的实际应用。但粒子滤波在易于实现的同时也会导致其他后果：（1）导致了更高阶的蒙特卡洛协方差，进而使预测效果变差；（2）使用先验概率作为建议分布之后，忽略了最新的系统观测值，可能导致粒子严重退化，即大多数粒子的权值都趋近于0，尤其是在似然函数达到峰值而预测的状态却在似然函数的边缘时。建议分布的取值在理论上有无穷多种可能性，但是最优的分布-权值的方差最小，即使存在，求解也十分困难。因此，选择1 个合理的建议分布，对于避免粒子退化、得到良好的滤波结果具有深刻意义。

1.2 无迹粒子滤波算法

上文已经指出了使用先验概率作为建议分布会导致系统缺陷，而改进建议分布最明显的方法是纳入当前观测的数据。于是学者设计出很多的卡尔曼滤波器来改进建议分布[18]，但是这些滤波器的表现多基于各自不同的近似假设。迄今为止，无迹卡尔曼滤波器是针对非线性系统表现最为优秀的卡尔曼滤波器。通过采用无迹卡尔曼滤波器产生合适的建议分布，可以将通用粒子滤波转化成高性能无迹粒子滤波。下文将讨论无迹卡尔曼滤波的基础——无迹变换，并且给出完整的无迹粒子滤波算法。

在许多现实应用中，都需要估计经过非线性变换y=g(x)的随机变量的低阶统计量，例如均值和协方差。无迹变换能够准确地计算出g(x)的泰勒级数展开不超过2阶的均值和方差。

假定n为系统变量x的维度，x的均值为，方差为Px，则通过无迹变换计算得到y=g(x)的均值和方差。

（1）确定2n+1个sigma点Si={Xi,Wi}。

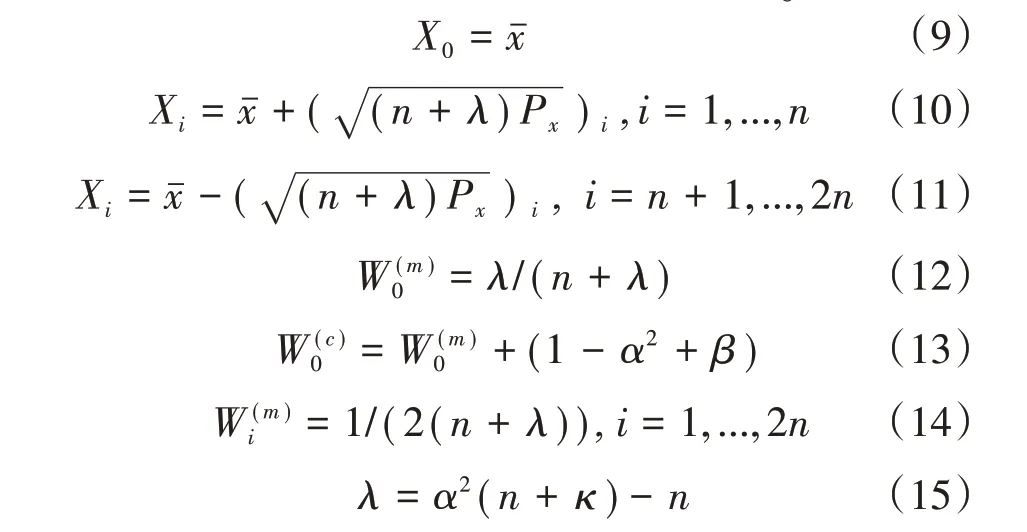
式中：κ为尺度参数，用来控制sigma 点与均值的距离；α为正的尺度参数，用以控制来自非线性函数g(x)的更高阶部分的影响；β为用来控制初始的sigma点权重的参数。

纵观现有的研究仍然存在着研究视角单一，对于组织边界、组织域的关注较少，缺乏对于组织机制及运作逻辑的结构性分析和建构过程的讨论。对于体育社会组织的制度约束、资源困境等关注过多，忽视了对于包括文化传统、道德习俗等非正式制度对于组织运作机制的形塑过程的分析，缺乏对于中国传统社会“合群立会”等历史视角的社会学想象力。从研究方法上看，个案研究过多，定量研究较少，从理论的解释力来看，理论与经验的不匹配、理论和方法背后的逻辑推演的不清晰，引进的西方理论的适用性等问题仍存在于目前的研究当中。

对于标量情况来说，最优值为α=0,β=0,κ=2。请注意，在计算平均值和协方差时，初始的sigma点的权重是不同的。

（2）通过非线性函数传播sigma点。

（3）计算y的均值和方差。

保证y的均值和协方差精确到泰勒级数2阶展开。

无迹卡尔曼滤波可以通过扩展状态空间以包含噪声分量来实现，即。而Na=Nx+Nm+Nn则是扩展之后的状态空间的维度，其中Nm和Nn是噪声mt和nt的维度，Q和R则是噪声mt和nt的协方差。整个UKF过程如下。

（1）初始化。

（2）按时间迭代。

a.用上述过程计算sigma点。

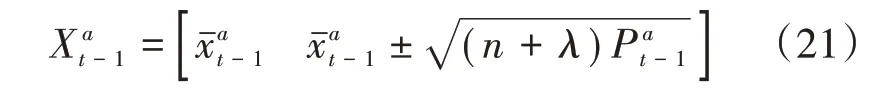
b.时间更新。

c.测量更新。

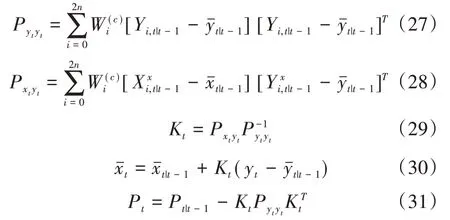
UKF 为2 阶近似，所以在准确度上要胜过1 阶近似的扩展卡尔曼滤波器（Extended Kalman Filter，EKF），而且在计算效率上同样优于EKF，因为UKF不需要计算雅克比矩阵和海森矩阵。

至此已讨论传统的粒子滤波及其不足之处，随后引入了无迹卡尔曼滤波。然而，无迹卡尔曼滤波对状态分布做了高斯假设。另外，对于粒子滤波，可以对任意分布进行建模，但是将新的观测加入到建议分布中并不容易。本文提出了改进办法，在航空发动机领域，利用UKF 来为粒子滤波生成建议分布，引进最新的观察来更新状态估计，即为无迹粒子滤波。对于每个粒子的取值概率分布明确为

值得注意的是，即使在估计后验分布p(xt|xt-1,y0:t)时高斯分布假设是不现实的，但对于每个粒子都有1个不同的均值和方差都不是问题。而且，使用UKF得到的均值和方差均达到2 阶展开，所以系统的非线性特性得以保存。将式（32）代入到传统粒子滤波算法中，即可得到UPF。完整的预测步骤如下。

（1）利 用式（21）～（31）的UKF 算法 来更 新,i=1,...,N，得到粒子的均值和协方差。

（3）利用式（5）计算出各粒子的权重。

（4）利用式（6）来归一化权重。

（5）计算有效的粒子规模大小S。

（6）如果有效粒子数少于有效数阈值，则对应生成N个等权粒子。

（7）利用式（7）来计算系统状态后验分布的期望值。xt的条件均值可以通过xt+1=f(xt)计算得到，而xt的协方差可以通过计算得到。可以使用计算得到的条件均值和协方差来得到发动机当前时刻排气温度的概率密度分布[19-21]。UPF 的流程如图1所示。

图1 UPF的流程

2 EGTM的预测算法及实现

2.1 EGTM预测过程

系统的测量方程和状态方程为

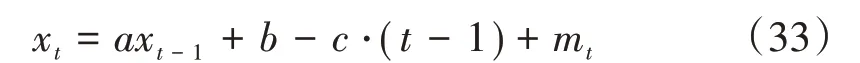
式中：a，b，c均为系数。

式（34）中的yt即为t时刻系统的观测值，是航空发动机EGT 的测量值与EGT 红线值的正差值，系统噪声和测量噪声均假定遵循高斯分布。根据粒子滤波方法，EGTM值估计为

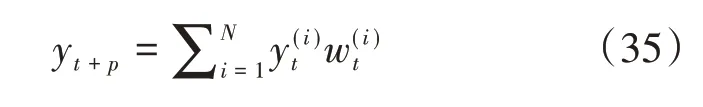
所以在t时刻的p步预测表示为

EGTM的后验概率密度为

当设定的EGTM 阈值为Y时，达到阈值的循环为L，则

所以在t时刻预测发动机在现有EGTM 条件下得到循环阈值的概率密度分布为

2.2 仿真结果分析

在本次仿真试验中，每次迭代中所取的粒子数均为100。采用无迹粒子滤波方法在18 和30 循环处对数据进行预测，状态方程的参数见表1。

表1 根据历史数据得到的状态方程参数

35 循环处传统粒子滤波方法的预测结果如图2所示。

图2 传统粒子滤波在35循环处的预测

由于没有考虑到最新的观测值，采用传统粒子滤波方法得到的数据与真实的发动机水洗循环数相差较多，预测概率密度是假定阈值为50 ℃时的数据，而当阈值为35 ℃时，预测的循环数在120 循环之后，与实际值相差较多。

在18 循环时刻的无迹粒子滤波预测结果如图3所示。

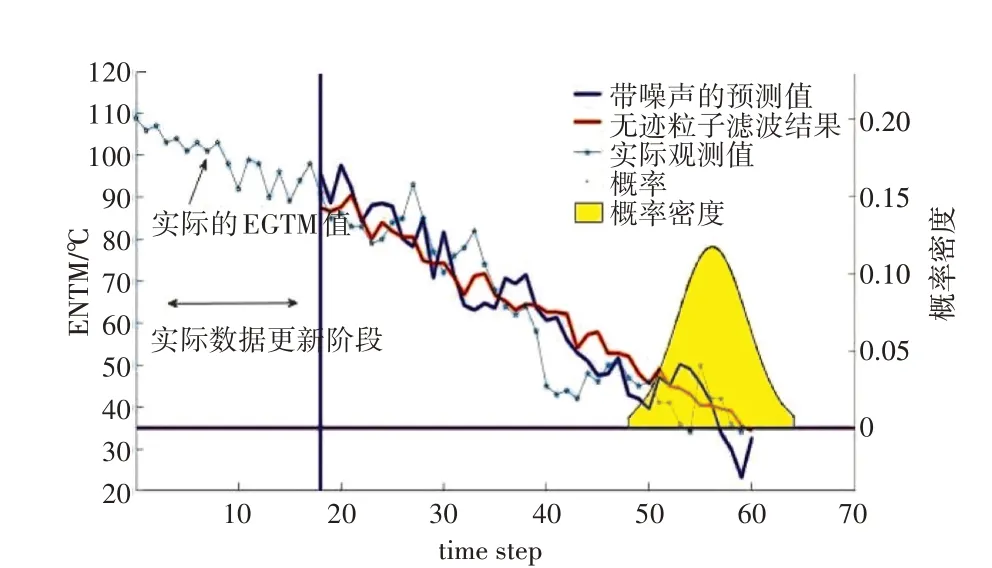
图3 无迹粒子滤波在18循环处的预测

前18 循环的航空发动机EGTM 实际数据将用来更新模型。从图中可见，在达到阈值35 ℃时，预测的最终循环数为60，而实际的飞行循环数为59，预测误差为1 循环，同时预测的EGTM 在阈值时的循环数的宽度为16。

前30 循环的发动机EGTM 实际数据将用来更新模型，如图4 所示。在达到阈值35 ℃时，预测的最终循环数为59，而实际的飞行循环数为59，预测误差为0 循环，同时预测的EGTM 在阈值时的循环数的宽度为7。从上述试验结果可见，因为有更多的实际数据用以更新模型，所以模型的准确度得到了提升，模型的拟合优度统计见表2。预测的循环数的宽度收窄了，说明预测的精度更高了。

图4 无迹粒子滤波在30循环处的预测

表2 拟合优度统计

3 结束语

随着民航产业的飞速发展，做好航空发动机性能衰退预测，对于发动机有效及时恢复性能和节约成本具有重要意义。针对发动机领域的特点，本文所提出的无迹粒子滤波算法作为一种改进的粒子滤波方法，充分利用了最新观测数据对系统模型进行修正，也降低了重采样对样本贫化的影响。因此，该方法不仅有抑制粒子退化的优点，而且在一定程度上保持了粒子的多样性。通过对无迹粒子滤波预测结果和传统粒子滤波计算结果的比较研究可知，无迹粒子滤波方法在预测的准确度（均值与真实值的接近程度）和预测的置信度（概率密度分布的狭窄程度）上都显示出巨大的优势。