陶瓷基复合材料力学性能计算及涡轮导叶宏观响应分析方法
刘 鑫 ,乔逸飞 ,董少静 ,申秀丽
(中国运载火箭技术研究院空天业务部1,空间物理重点实验室2:北京 100076;3.北京航空航天大学能源与动力工程学院,北京 100191)
0 引言
为了不断提高航空发动机推重比,对高压涡轮导叶等高温部件的耐高温能力的要求将越来越高。目前推重比15~20 一级的发动机涡轮前温度已经高达1900~2100 ℃[1]。SiCf/SiC 陶瓷基复合材料(Ceramic Matrix Composite,CMC)因具有耐高温(最高使用温度可达1450 ℃[2])、耐腐蚀、低密度的优点,不仅满足高压涡轮导叶工作超高温度要求,还可以减轻导叶质量,提高发动机推重比。
完整的材料性能参数是CMC 涡轮导叶结构强度分析的基础,为获取力学性能参数,开展大量的试验,时间和经济成本较高。同时,2D 编织CMC 面内力学性能参数可通过试验测得,而面外法向的力学性能参数很难通过试验测量[3]。一般通过描述CMC 的细观结构特征建立代表性体积单元(Representative Volume Element,RVE)模型,结合特定的数值计算方法,预测CMC 宏观材料参数[4-5]。但多数RVE 模型对材料的细观特征大幅简化,与真实结构有较大差距,无法准确描述细观参数对材料性能的影响[6]。尤其对化学气相沉积(Chemical Vapor Infiltration,CVI)工艺制备的CMC,材料孔隙率一般在10%以上,真实细观结构较为复杂[7]。Chateau等[8]讨论了孔隙对单向纤维增强SiCf/SiC 复合材料弹性性能的影响,表明孔隙率从4%增加到9%,复合材料横向模量降低了50%[8]。因此有必要建立考虑缺陷特征的细观RVE 模型来预测材料的力学性能。
目前主要的材料性能数值计算方法包括通用单胞模型法[9]、双尺度渐进均匀化方法[10]和细观有限元法[11]。其中细观有限元法不受模型复杂程度的影响,可以在考虑缺陷的RVE 模型基础上开展计算,使数值预报结果更为准确,且实现过程简单,是目前应用较为广泛、成熟的数值计算方法。李波等[12]针对单向纤维增强复合材料建立了描述孔隙缺陷的RVE 模型,结合细观有限元法讨论了孔隙缺陷对材料力学性能的影响;McWilliams 等[13]、CHEN 等[14]、WANG 等[15]分别建立2D、2.5D及3D编织RVE模型,通过细观有限元法预测了材料宏观力学性能。可见细观有限元法对不同预制体结构的复合材料均具有较好的适用性。
编织结构复合材料为正交各向异性材料,对于CMC 涡轮导叶等复杂的形状构件,材料的局部坐标系是随结构不断变化的[16]。因此在完整材料性能参数基础上预测CMC 涡轮导叶宏观应力应变响应时,先针对导叶结构和工艺特点描述有限元模型的材料分布情况,以保证数值仿真的准确性。Brewer 等[16]、Verrilli 等[17]对CMC 导叶有限元模型施加局部材料坐标,计算得出导叶的宏观应力应变分布,在热载荷下导叶尾缘位置出现较大应力,可见尾缘位置为CMC涡轮导叶宏观响应分析的关键位置。
基于以上国内外研究,本文利用细观有限元计算方法,通过一种考虑缺陷位置及形状的CVI 工艺2D编织复合材料RVE 模型预测了SiCf/SiC-CMC 各方向的宏观力学性能。开展面内拉伸、剪切力学本构试验并对预测结果进行验证。结合CMC 涡轮导叶典型结构的加工工艺,建立材料分布映射模型,预测了典型结构在给定条件下的宏观应力应变响应。
1 2D编织结构RVE模型
2D 编织CVI 工艺SiCf/SiC-CMC 细观编织结构如图1所示。
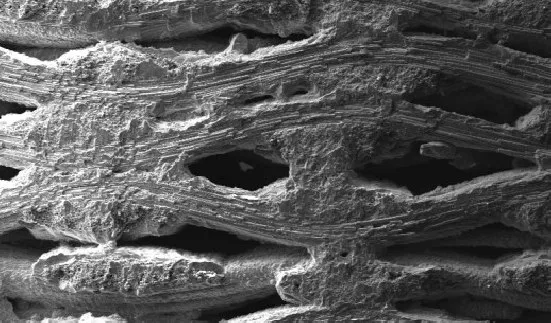
图1 2D SiCf/SiC-CMC细观编织结构
CVI工艺2D编织结构CMC 细观结构具有如下特征:(1)预制体均匀分布,纤维束截面形状保持一致,纤维束间通过基体连接;(2)纤维束表面基体厚度基本相同,单层SiC基体沉积完成后该层即封闭;(3)孔隙分布于基体内,位置和形状大致满足周期分布的特点。
根据以上特征,通过对材料不同位置电镜扫描(Scanning Electron Microscope,SEM)图片进行统计分析获取编织结构建模特征参数,如图2 所示。对2D编织SiCf/SiC 试验件进行分割,观测并统计材料不同位置的SEM图像,最终得到RVE模型参数,见表1。表中,w为纤维束截面宽度;t为纤维束截面厚度;p为相邻纤维束截面中心间距;h为RVE厚度;s为基体宽度。

图2 细观编织结构建模参数
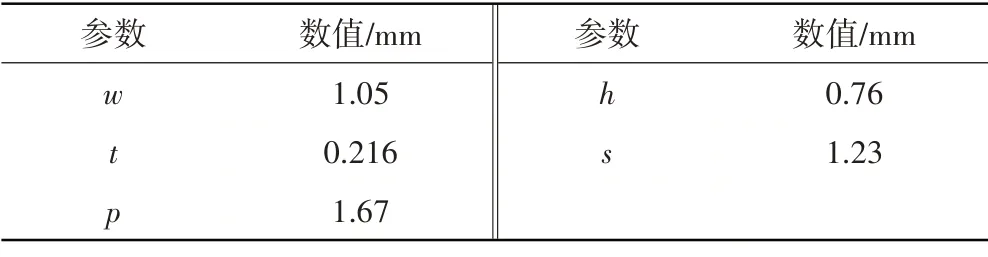
表1 2D编织SiCf/SiC-CMC细观建模参数
根据以上参数,建立了本文研究的CVI 工艺2D编织SiCf/SiC复合材料RVE模型,如图3所示。
山洪预警指标FFG是指可引发山洪的时段降雨量,在美国通常是指1、3、6小时三个固定的时间段。需要说明的是:FFG是指预报河流断面上游流域上的平均雨量;由于山洪不仅与当前降雨有关,还与小流域下垫面条件、前期洼蓄量、土壤湿度等因素有关,在不同条件下,导致某一山洪沟发生洪水所需的降雨量也不同,因此FFG不是一个固定值,而是一个需要估算的动态变化值。
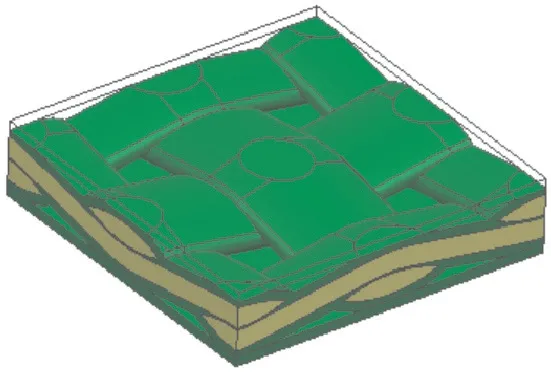
图3 2D SiCf/SiC-CMC编织尺度RVE模型
2 CMC弹性性能计算及试验验证
本文采用细观有限元法对CMC 宏观弹性性能进行预报。目前采用细观有限元法开展的复合材料计算中,大多采用统一周期边界条件对RVE 模型进行约束。在统一周期边界条件下,除加载方向外,其他方向对应面的节点相对位移为零,统一周期边界条件模拟的是在空间内有无数RVE 模型相连的情况,RVE 模型对应点的变形和应力完全相同。而实际力学本构试验中的试件宽度为10 mm,仅包含4~6 个单胞。另外,施加的统一周期边界条件要求RVE 模型对应面上的网格完全一致,对于考虑缺陷建模的有较复杂结构的RVE 模型,周期性分网是比较困难的。因此,对RVE 模型中除加载方向外的对应面采用自由边界条件,不进行约束,计算得到的弹性常数也具有很高准确性[18]。
基于均匀化思想,在预测弹性性能时,可将2D编织SiCf/SiC 复合材料视为均匀正交各向异性弹性体,其等效本构关系为

RVE 模型平均应力、应变可以通过RVE 模型每个单元应力及应变得到
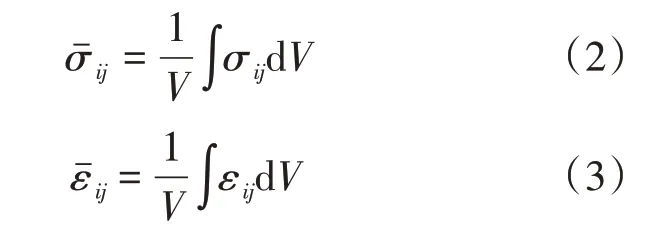
式中:σij、εij分别为每个单元的应力和应变;V为RVE模型的体积。
通过以上积分公式求得;在施加统一周期边界条件时设置。材料的弹性常数为


表2 纤维束的力学性能[19]
基体为各向同性,其弹性模量为227.8 GPa,泊松比为0.2[19]。本文所研究的SiCf/SiC 复合材料界面层厚度较小,在微观结构SEM 图像中几乎难以辨别,开展弹性性能预测时微观模型中界面层可以忽略不计。在纤维束和基体力学性能基础上,分别取各方向应变为0.05%(所取应变值应在弹性范围内),采用细观有限元法计算得到2D 编织SiCf/SiC-CMC 力学性能。为验证计算方法的准确性,通过力学本构试验测得材料面内拉伸、剪切模量,见表3。

表3 2D编织SiCf/SiC-CMC力学性能试验结果
数值模拟与试验结果对比见表4。表中:下角标x、y为面内方向,z为面外法向。面内拉伸和剪切模量通过试验测量分别为190 GPa 和71 GPa,预测值与试验值误差在8%以内。可以将计算得到的材料性能参数用于后续CMC涡轮导叶宏观热力学响应分析。

表4 2D编织SiCf/SiC-CMC数值模拟值与试验值对比
3 CMC涡轮导叶典型结构热载荷试验
对2D 编织SiCf/SiC-CMC 涡轮导叶典型结构进行热载荷下的宏观响应试验,试验件如图4所示。通过叶身上的安装孔固定试验件及换热金属,由于CMC 具有不导电的特性,在试验时先感应加热金属片,再通过金属加热试验件。

图4 CMC涡轮导叶典型结构及加热装置
通过热电偶监测试件加热区域温度变化,在试验稳定时测得温度为638 ℃。通过非接触式全场应变仪(Digital Image Correlation,DIC),测得CMC 涡轮导叶典型结构尾缘处的平均第1 主应变为0.00328,如图5 所示。该结果可用于验证宏观响应计算方法的准确性。

图5 CMC导叶典型结构试验段尾缘第1主应变
4 CMC导叶典型结构宏观响应计算
4.1 材料映射模型
在叶片加工时以2D 编织SiC 纤维布进行铺层,采用CVI工艺得到叶型毛坯件,再利用机械加工得到CMC 导叶。叶身切割解剖如图6所示。材料局部坐标系随构件形状而变化,但其材料分布仍保持连续性,RVE 沿叶身弧线分布均匀,材料主轴根据纤维布编织方向和曲面形状确定。

图6 导叶叶身切割解剖典型结构
材料分布模型包括2部分:
(1)面内材料以纤维束经向或纬向作为第1 主轴方向(经向与纬向相互垂直,选择便于描述的作为主轴方向);
(2)导叶叶型曲面的局部法向作为第3 主轴方向。第2 主轴方向由第1、3 主轴方向利用右手定则惟一确定。通过材料分布模型对有限元模型施加局部材料坐标,如图7所示。

图7 导叶典型结构有限元模型中某单元的材料局部坐标
4.2 典型结构热响应计算
采用宏观温度场计算时,在上缘板安装边表面和叶片底部平面设置室温25 ℃,中间加热部分温度设置638 ℃,与试验温度保持相同。2D 编织SiCf/SiCCMC 的导热系数λ和热膨胀系数α见表5。根据复合材料均匀化思想,在构件计算中忽略RVE 模型的细观结构,保留材料性能数值和主方向,采用热固耦合分析方法[20]计算得到的导叶典型结构温度场分布如图8所示。
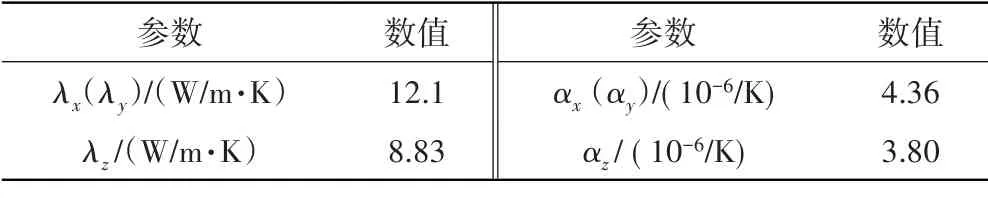
表5 2D编织SiCf/SiC-CMC热物理性能[20]
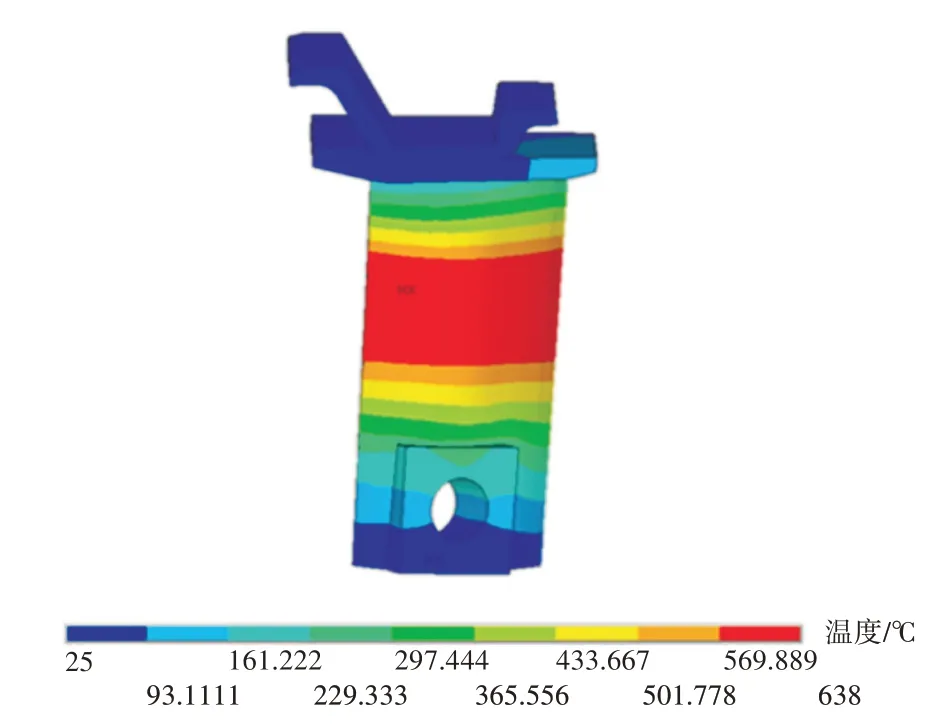
图8 导叶典型结构温度场分布
在安装孔设置沿x、y、z方向的位移约束作为结构分析施加的边界条件。计算得到的叶身加热段x方向(轴向)应力分布如图9 所示,其最大应力值为24.6 MPa;y方向(周向)应力分布如图10 所示,其最大应力值为20 MPa;z方向(径向)应力分布如图11 所示,其最大应力值为169 MPa。从图中可见,导叶沿径向温差较大,导致沿径向的应力也较大,试验测得2D编织SiCf/SiC-CMC 径向拉伸强度为259 MPa,在本文给定的热载荷下不会导致叶片失效损坏。
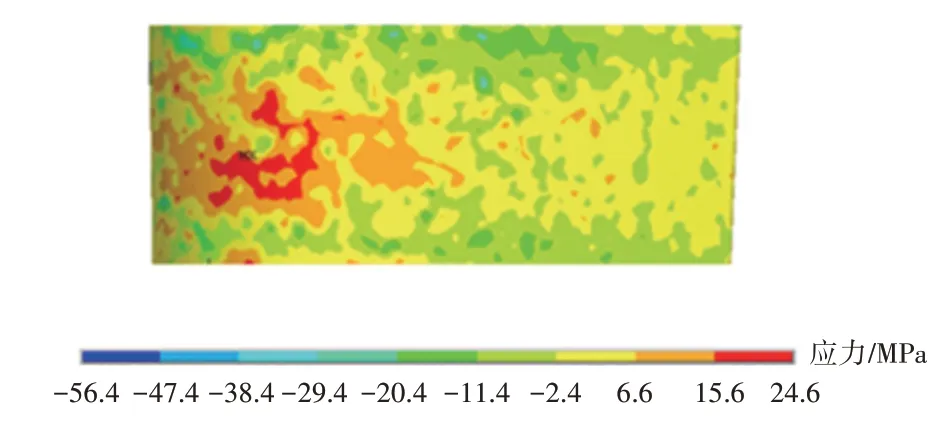
图9 加热段x方向(轴向)应力分布
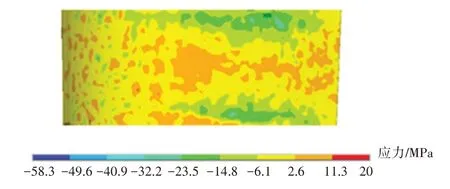
图10 加热段y方向(周向)应力分布
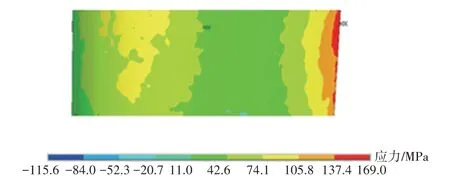
图11 加热段z方向(径向)应力分布
根据数值模拟结果,叶片的最大径向应力出现在尾缘部分,叶片尾缘为计算校核的关键位置。CMC涡轮导叶尾缘加热段第1 主应变分布如图12 所示。叶片尾缘平均应变计算值为0.00310,而热加载试验值为0.00328,相对误差为5.5%。可见通过构建材料映射模型对CMC 典型结构宏观热响应的计算具有较高的准确性。
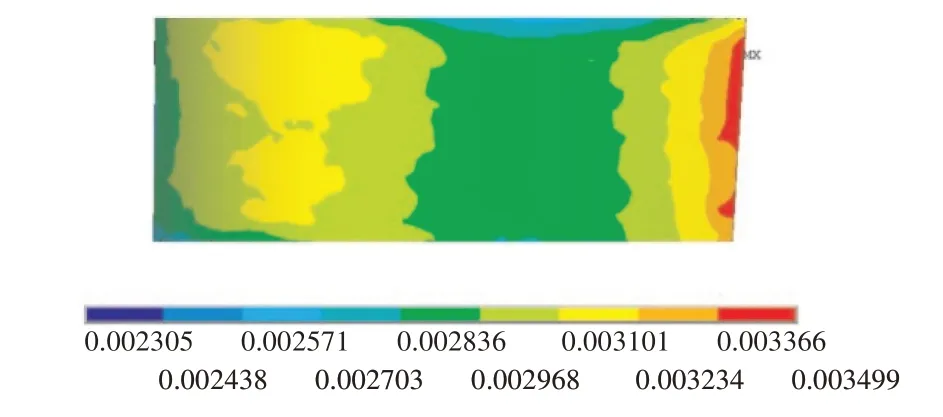
图12 加热段第1主应变分布
5 结论
(1)本文对2D 编织SiCf/SiC-CMC 进行断面电镜扫描,测量统计RVE 模型特征结构参数,建立了考虑孔隙形状、大小、位置的CVI 工艺2D 编织RVE 模型,该模型与真实结构具有良好的一致性。结合细观有限元方法,利用本文建立的RVE模型,计算得到2D编织CVI 工艺SiCf/SiC 复合材料的完整力学性能参数。面内拉伸模量预测值比试验值低4.4%,剪切模量预测值比试验值高7.8%,证明了性能预测方法有效。
(2)根据CMC 涡轮导叶典型结构加工工艺特点,建立了材料映射分布模型,结合预测得到完整的SiCf/SiC-CMC 力学性能参数,计算了涡轮导叶典型特征结构在一定温度下的宏观热响应。通过典型结构热载荷试验测量得到加热段尾缘的第1 主应变,预测值比试验值低5.5%,证明了该计算方法有效。

