风扇整体叶盘振动响应数值仿真及试验验证

刘一雄 ，杜 青 ，陈育志 ，徐可宁 ，丛佩红 ，莫 妲

（1.中国航发沈阳发动机研究所，沈阳 110015；2.辽宁省航空发动机冲击动力学重点实验室，沈阳 110015；3.中国航空发动机研究院，北京 101304）

0 引言

航空发动机叶片/盘设计的主要任务之一就是确保在工作转速范围内不发生有害共振，在工程上常常结合振动特性分析结果绘制坎贝尔图，评估叶片的共振转速裕度进而采取避开共振转速的措施，然而由于无法对真实的振动应力进行精确预测，仅能预测到可能存在的共振转速和振型，这种方法受到较大的限制，只适用于设计初期对叶片的共振情况的初步了解。

为了获取叶片/盘的真实振动响应，国内外学者开展了较多研究工作。Kielb 等[1]针对涡轮叶片尾流激振的强迫响应开展了数值模拟和试验验证；Sayma等[2]建立了非线性振动响应预测模型；赵书军[3]在3维流场计算的基础上，采用ANSYS 软件开展了谐响应分析，获得了叶片的稳态受迫振动响应；邵帅等[4]采用模态局部化因子评价了失谐叶盘的振动模态局部化问题；王梅等[5-6]研究了将前排静子叶片尾流场作用下叶片非定常流场转换为结构载荷压力场的形式，结合实测阻尼，求解出转子叶片的响应，建立工程适用的振动应力预估半经验方法；王营等[7]采用流固耦合的方法计算了宽弦空心风扇叶片的响应，给出了叶片的位移响应；张大义等[8]完善了双向顺序耦合求解理论，计算了静子叶片在气流激励下的响应；弓三伟等[9]利用CFX 和ANSYS软件，采用单通道耦合模型计算了稳态载荷作用下叶片的位移和应力；张明明等[10]同样利用上述软件，开展了压气机转子全周3 维进气畸变数值模拟，并考虑了双向耦合作用；徐可宁等[11-12]发展了3 维叶轮机气动弹性计算软件系统，基于时间推进方法求解转子叶片的瞬态位移及动应力，并开展了压气机转子错频对叶盘结构的振动响应影响分析；牛永红等[13]研究了非均匀静子布局对转子叶片振动响应的影响；王娇[14]利用解析法与有限元方法相结合，考虑了不同气动载荷加载对叶片振动响应的影响。

上述研究大多采用流固耦合方法开展叶片的振动响应分析，只不过在方法上区分弱耦合或强耦合。随着计算机技术的发展，流固耦合求解振动响应必然成为叶片共振设计的发展方向。实际上，整体叶盘结构的振动响应求解与叶片结构并无本质区别，然而与传统榫连叶/盘结构相比，整体叶盘的盘体更薄，盘叶耦合性更强，必须开展耦合共振分析[15]，与单个叶片的坎贝尔图不同的是，整体叶盘的坎贝尔图交点极多且复杂，在工作范围内避开所有共振点是无法实现的，如何合理选取危险振型开展响应分析是工程设计中的一大难点。同时，整体叶盘结构是无榫设计，无法设置缘板阻尼器、难以设计凸肩拉筋叶冠等常规摩擦阻尼结构，阻尼通常较小[16]，进行响应分析时阻尼的正确选取关系着计算结果的正确性。

本文在风扇整体叶盘耦合振动分析的基础上，绘制耦合共振坎贝尔图，结合工程设计经验，给出危险振型筛选原则，获得叶片真实振动应力，并通过台架整机动应力测量进行试验验证。

1 研究方法及模型

本文的研究对象为风扇整体叶盘，其受尾流激振、进气畸变等因素形成的非均匀气动激振较为明显，由强迫振动导致的高周疲劳失效问题更为突出，有必要开展响应预测技术研究和验证。

研究由静子尾流非常定气动力引起的叶片振动，理论上应该考虑叶片振动与非定常气动激振力之间的耦合作用，但这需要巨大的计算成本[17-18]。基于工程应用的目的，本文忽略叶片振动与气动非定常力之间的耦合作用。

风扇叶盘的材料为TC17合金，密度为4640 kg/m3，弹性模量为113.5 GPa，泊松比为0.3。采用20节点六面体单元对叶盘进行网格划分，1/20有限元模型如图1 所示。进行流场分析时建立了考虑前后级静子叶片的整环非定常流场模型，其中转子和前、后排静子的叶片数分别为20、23、45，流场模型如图2所示。

图1 风扇整体叶盘扇段有限元模型

图2 风扇整体叶盘非定常流场分析模型

2 振动响应分析

针对整体叶盘结构盘片耦合效应强、振型复杂的情况，为了准确识别风扇整体叶盘结构的危险振型，给出了振动响应分析流程，如图3所示。

图3 振动响应分析流程

2.1 危险振型识别

首先对风扇叶盘开展振动特性分析，通过在盘体切割面施加周期对称边界条件模拟整个叶盘，并通过摄动分析考虑了几何非线性的影响。在危险节径判定方面，中国学者开展了较多研究，王延荣等[15]探讨了如何确定盘片耦合结构的危险节径数，姚建尧[19]提出振型节径谱对失谐叶盘进行分析，乞征等[20]和李琳等[21]通过转静干涉激励的角度对危险激励阶次进行分析，本文在文献[22]中提出的危险节径与转、静子叶片数关系的基础上，根据式（1）计算得到可能存在的危险节径，见表1。同时，根据“激励阶次等于节径数会激起危险共振”的原则，考虑机匣椭圆度的影响，绘制了耦合共振图，如图4所示。

图4 低阶盘片耦合振动坎贝尔图

表1 与静子叶片数相关的危险节径

式中：dm为危险节径；k为激励阶次；NS为前排或后排静子叶片数；n为整数；NR为转子叶片数。

结合耦合共振图，通过计算共振转速裕度，给出了前10 阶振型下可能存在的危险共振转速和共振频率，见表2。

表2 低阶危险共振转速计算结果

2.2 非定常流场分析

在表2 获得的共振转速的基础上采用CFX 软件开展非定常流场分析，以2E激起的2节径1阶共振为例进行说明，首先对所有排叶片进行单通道定常分析，提取图2 中的3 排转、静子叶片的进、出口边界条件并扩展至全环，该计算模型既考虑了上游叶片的尾流激振，也考虑了下游叶片势流扰动对上游叶片的影响。流场网格节点总数为3000 万，湍流模型为k-ξ模型，近壁面采用标准壁面函数。进行非定常计算时选取瞬态计算模块，时间步长定义为扫掠过后排静子叶片每个通道的1/40。将振荡收敛后最后1 个周期内叶片表面的气动压力进行拓展后作为响应分析的输入条件。在计算过程中通过设置谐波数考虑了机匣椭圆度2E～6E的影响，每个共振点的非定常气动力计算耗时约为1周。

计算得到的风扇叶盘静压分布如图5 所示，叶尖前缘监测点的静压随时间的变化曲线如图6所示。

图5 某时间点叶片表面压力分布

图6 叶尖上某点沿时间静压

2.3 振动响应预估

进行振动响应分析时首先将非定常气动力转化为随时间变化的节点压力，施加于风扇叶盘有限元模型上；采用模态叠加法对叶盘进行瞬态响应分析。其中阻尼的选取对响应计算结果有较大的影响，对于本文的计算模型，通过敲击法获得叶片模态阻尼比。

2.3.1 阻尼测试

用力锤敲击叶盘，采用自由振动衰减法计算获得叶盘的模态阻尼比

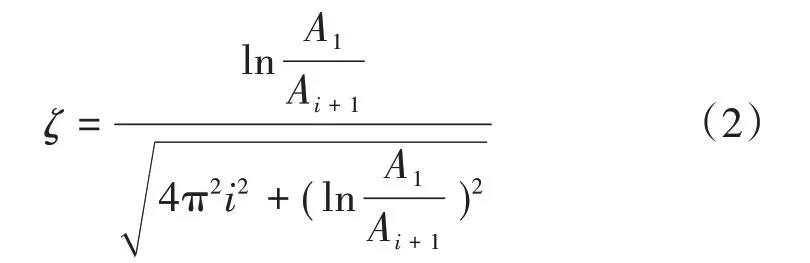
式中：ζ为阻尼比；i为参与计算的波的个数；A1、Ai+1为参与计算的首、尾波峰值。

进行数据处理时将实测的含有多阶频率的信号通过数字带通滤波处理分离成各目标阶次频率的单频振动信号，进行时域阻尼比计算以获得各阶振动频率对应的阻尼比。并采用峰值拾取法将频响函数分成实部分量和虚部分量，直接从实、虚频图上读取数据后进而获得模态参数。

在试验过程中可能带来误差的有测试系统、敲击力大小、数据分析方法及应变片贴片位置等因素。因此，周向随机选择3 片叶片在叶尖相同部位粘贴应变片，并在力锤上连接传感器，取相同的敲击力下叶盘的测试结果，进行多次敲击试验后取模态阻尼比的平均值。前3 阶的频率和对应的模态阻尼比的平均值见表3。

表3 叶片前3阶频率及其阻尼比

2.3.2 响应预估

以1 弯振动响应预估为例进行说明。首先开展考虑离心载荷的静力学分析，然后进行包含预应力的瞬态响应分析。将第2.2节中获得的叶片表面随时间变化的非定常气动载荷插值到有限元模型，作为叶片表面节点压力，在时间域内开展响应分析；同时，对于前3阶模态阻尼比按表3中试验获得的数据以瑞利阻尼形式给出。对于高阶模态阻尼比的选取，考虑到整体叶盘没有榫连结构、凸肩等结构阻尼件，忽略结构阻尼的影响，主要考虑材料阻尼，在真空条件下将叶片根部固支，获得了钛合金弯曲模态的材料阻尼比为0.0003，扭转模态的材料阻尼比为0.0001[16]，本文将此数据作为高阶阻尼以瑞利阻尼形式给出。

选取叶盘根部最大振动应力部位作为监测点，如图7 所示。经过若干周期计算迭代后，叶盘表面监测点的振动应力趋于收敛，如图8 所示。此时计算得到的振动应力为叶盘真实振动应力，稳定后的A点振动应力为35 MPa，整圈叶盘的振动应力分布如图9所示。

图7 2节径1弯振型监测点

图8 1弯振型下收敛稳定后的应力幅值

图9 1弯振型下振动应力分布

3 试验验证

为了摸清风扇叶盘的真实振动情况，验证振动响应计算结果的精度，在风扇叶盘上粘贴应变片并开展整机动应力测量。贴片方案（如图10 所示）依据振动特性和振动响应计算结果制定，主要考虑前5 阶模态的振动应力大点。其中A点主要用于监控1 阶弯曲振动，贴片位置与图7 中监测点A的位置一致，周向连续的5 个叶片上均在A点粘贴应变片。H、L1和L2为无量纲尺寸。

图10 应变片贴片方案

将整机动应力试车结果与计算结果进行对比分析，见表4。通过周向连续粘贴应变片的相位分析结果及光纤测量结果，判定A位置发生了2节径1弯振动，计算的振动应力与实测结果吻合较好。

表4 数值仿真与试验结果对比

表中C、D位置的数值仿真结果与试验结果存在一定误差。带来误差的可能原因有计算振型选取、激振力计算精度和阻尼比给定。频率对比分析结果表明，计算频率与实测频率基本一致；试验时在同一叶片3 个不同部位均粘贴应变片，通过所测的3 个部位应力比值与有限元计算结果进行对比，确定计算振型与实测结果基本一致，上述分析可以确定计算振型的准确性。影响转子叶片振动响应的主要是前、后级静子叶片的激励，在进行非定常流场分析时建立了考虑前后级静子叶片的模型，通过设置较小的计算步长，可以捕捉到高阶激振的频率信息，并且低阶计算的准确度也验证了算法的精度。由于高阶频率对应的阻尼比是通过参考文献给出的，考虑到文献中叶盘尺寸、造型、材料性能与本文研究的叶盘有所不同以及受失谐等因素的影响，高阶阻尼比的给定存在一定误差。综合分析认为，高阶振动应力预测存在误差的的主要原因是选取的阻尼比与实际略有偏差所致。

4 总结

本文基于弱耦合方法开展了风扇叶盘结构的振动响应数值模拟研究，通过3 排叶片全环非定常流场分析获得了随时间变化的转子叶片表面的气动压力，可以较好地模拟前后排静子叶片带来的影响，响应分析采用实测的模态阻尼比，提高了计算精度，经验证，数值模拟结果与试验结果吻合较好，可以满足工程使用要求。