航空航天用CQFP 封装复杂集成电路振动夹具优化设计
王小强,李 斌,邓传锦,罗 军,余永涛
(1. 华南理工大学 电子与信息学院,广州 510640; 2. 工业和信息化部电子第五研究所,广州 511370)
0 引言
强推力、大负载的飞行器,在发射、起飞、飞行等过程中会产生宽频、高量级的振动,这对航天航空装备用集成电路产品的力学环境适应性和可靠性提出了更高要求,因此产品必须要经过振动试验的考核。夹具作为振动台与试验产品的连接部件,其设计是振动试验中的一个重要环节[1],但目前我国仍未有关于集成电路振动试验夹具设计要求的相关标准。航空航天用复杂集成电路产品以及更严酷的试验条件对振动试验夹具设计方法提出了挑战:根据MIL-STD-883K[2]及GB/T 2423[3-4],航空航天用装备的振动试验频率要求为20~2000 Hz,正弦加速度为20g~50g或随机振动加速度均方根值为16.9g~29.2g。由于复杂集成电路芯片管脚数量可达上千,封装复杂且难于刚性固定,导致其振动试验夹具在安装后整个夹具系统结构刚度下降,可能造成能量传递失真,在试验频率范围内易引发共振或传递振动量级超过允许误差范围。
计算机仿真技术的发展使得振动夹具的设计从多次经验设计与修改,甚至是多版本实物夹具更新的迭代,发展为“设计—仿真分析—优化改进设计”的路线。而目前基于有限元软件开展的振动夹具优化设计方法研究[5-9]大多只对夹具的材料、结构及尺寸的某一方面进行仿真优化,未能对夹具进行全面的优化设计,缺乏实际参考价值。同时,由于仿真及夹具制作等过程存在误差因素,实际制作的夹具在振动试验中还可能存在响应均匀性差、共振等不足。
本文针对航空航天应用环境条件以及复杂集成电路产品振动夹具设计的高标准技术需求,选用典型CQFP228 封装航空航天用复杂集成电路芯片,合理设计振动夹具:建立有限元模型,采用基于拓扑优化和尺寸参数优化的集成电路振动夹具综合优化设计方法,并进行夹具的扫频振动以及随机振动响应仿真分析和试验验证,旨在为航空航天用复杂集成电路产品振动试验夹具优化设计提供参考。
1 夹具设计要求与流程
1.1 设计要求
参考集成电路常用振动试验标准、美国桑地亚公司提出的夹具标准[10]以及振动夹具设计相关文献[1,11],本文提出对复杂集成电路振动试验夹具的基本要求:
1)可方便地与振动台面和试件连接,并且应方便更换试验方向以及安装更多试验样品;
2)为减少振动传递的失真,应尽量使夹具在试验频率范围内无共振;
3)夹具质量应尽可能小,因为夹具的质量直接影响振动系统的总质量,影响振动台装上试件后所能达到的最大加速度数值。
为保证传递到样品的试验应力符合标准要求,夹具的传递性能应符合标准中对样品的试验要求:扫频振动2000 Hz 内加速度响应偏差在±20%以内;随机振动1000 Hz 内功率谱密度响应偏差在±1.5 dB 以内,1000~2000 Hz 功率谱密度响应值偏差在±3 dB 以内。
1.2 设计流程
复杂集成电路振动夹具设计流程如图1 所示。首先依据夹具设计目标进行初始形状与功能设计;再基于有限元仿真分析对初始方案进行评估与修改;然后再使用拓扑优化和结构尺寸参数优化设计方法对夹具进行优化;对优化后的夹具模型进行扫频振动以及随机振动响应仿真分析,最终使设计的夹具满足模态特性、质量要求、传递性能等多方面指标要求;生产加工夹具并对其进行试验验证,以验证夹具是否满足设计要求;若不满足,则继续交互使用拓扑优化和结构尺寸优化设计方法对夹具进行优化,直至其通过试验验证。
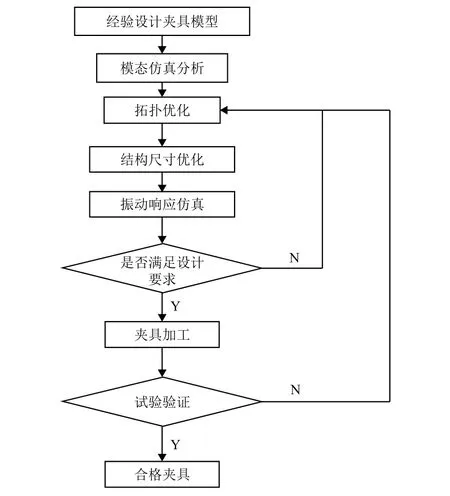
图1 集成电路振动夹具设计流程Fig. 1 Flowchart for integrated circuit vibration fixture
2 结构设计
2.1 设计对象及振动载荷
以某型航空航天用CQFP228 封装集成电路为例,其样品见图2。该芯片管脚数量达到228 个,管脚间距为0.5 mm。其应用环境的抗振性能要求:正弦振动试验频率为20~2000 Hz,加速度20g;随机振动试验频率为50~2000 Hz,功率谱密度20 (m/s2)2/Hz。

图2 CQFP 封装集成电路Fig. 2 CQFP packaged integrated circuit

2.2 振动试验夹具结构设计
按图1 设计流程,根据前文的夹具设计需求,结合常见集中夹具组合结构类型的用途与特点[12],初步确定采用6061 铝合金材质、六面体子母夹具组合结构的设计方案。六面体的母夹具(见图3(a))底面可以与振动台连接,其余面均可与子夹具连接,这样可较高效率地实现受试样品转换试验方法的要求。而子夹具(见图3(b))则根据试样的外观尺寸,设计相应的凹槽以安装试样,用盖板或较细的压条压紧试样以保证试样与夹具刚性接触。
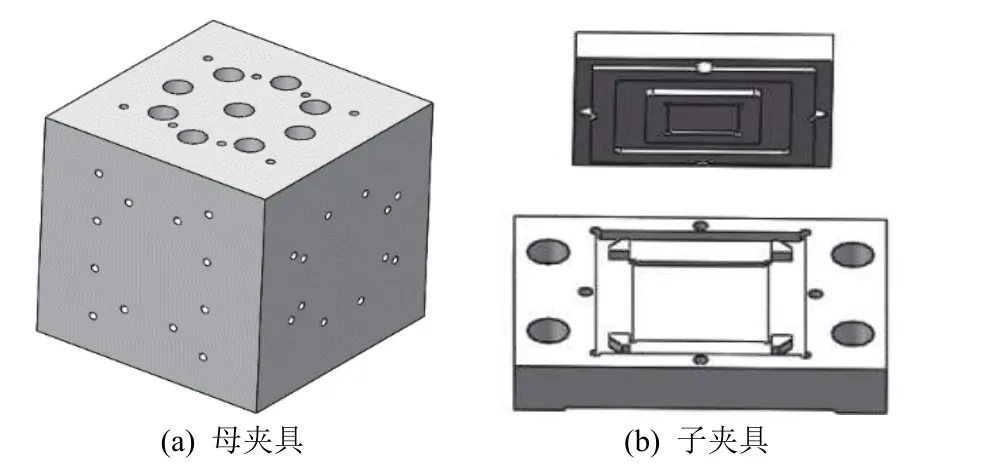
图3 子母夹具组合的夹具结构Fig. 3 The fixture structure of base fixture and sub-fixture
该夹具结构模态仿真结果如表1 所示。结果表明:子夹具一阶固有频率远超2000 Hz,并且质量较轻,可不需要优化;而母夹具及夹具装配体前两阶固有频率较接近2000 Hz,并且质量过大。为确保试验时夹具的模态特性符合要求,并尽量降低夹具质量,需要使用上述优化方法进行设计改进。

表1 初次设计夹具的模态仿真结果Table 1 Simulated modal results of initial design of the fixture
3 振动夹具设计优化
3.1 布局优化
相对于尺寸优化和形状优化,拓扑优化具有更多的设计自由度,使用的有限元模型不需要参数化,能够获得一个正确的结构优化布局。因此,首先对夹具进行拓扑优化。
本优化中夹具为连续体结构。连续体拓扑优化方法主要有[13]SIMP 变密度法、均匀化方法和水平集法。其中,SIMP 变密度法基于各向同性材料,以区间[0,1]内的相对密度作为拓扑设计变量,通过定义经验公式,人为假定相对密度和材料弹性模量之间的非线性关系,寻求结构最佳的传递路线,以实现优化设计区域内的材料分布[14-15]。该方法可以得到边界清晰、规则的结构,并且较为成熟,已集成于大部分商业有限元软件中,具有程序易实现、计算效率快、计算精度高的优势。本拓扑优化设计具体采用ANSYS Workbench 软件的SIMP 变密度法实现。
为了减少分析的运算量以及出现不合理的可能性,在建立拓扑优化夹具有限元模型时,需要对模型进行必要的简化。简化的原则是删除对结构刚度影响不大但对模型的复杂程度影响很大的小构件、小孔、倒角及圆角等细节特征。本算例中去除夹具上螺孔中的螺纹以及倒角等细节。
选择优化区域时,由于母夹具底部采用螺栓与振动台固定,底部中间有固定孔,并且六面体中五个面设计螺孔用于将子夹具固定,故除固定孔与螺孔这两部分外其他部分均需优化。为提高优化效率,优化过程以材料分布最优为约束,一阶频率大于2000 Hz 为目标,且限定优化结果在迭代次数100 次内满足收敛条件。拓扑优化的约束条件及目标函数为
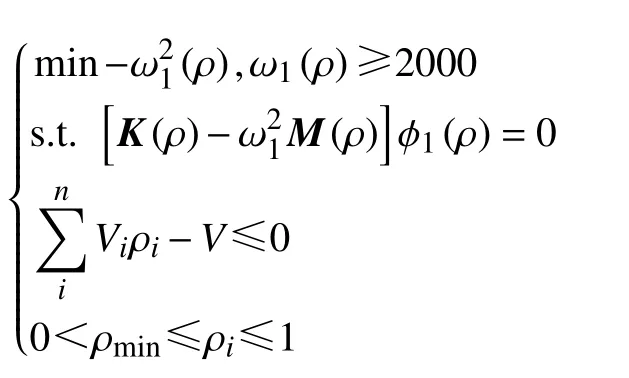
式中:ω1和φ1分别为结构的一阶固有频率和振型;ρ=[ρ1,ρ1,…,ρn]T是有限元离散的单元的当量密度;K(ρ)为结构的整体刚度矩阵;M(ρ)为整体的质量矩阵;Vi和V分别为单元体积和目标体积;ρmin是为防止零密度造成整体刚度矩阵奇异而设定的密度下限,一般取为0.001。由图4 可以看出,在迭代第39 次时,系统收敛到最优解。通过图5 拓扑优化结果可以得到优化后的大致形状。根据结果采用两种方式改进结构形状:1)将不连续边界缺失单元填充;2)将多余单元删减,使边界连续。改进后的母夹具结构如图6 所示。

图4 夹具优化迭代过程Fig. 4 Iterative process of the fixture optimization

图5 拓扑优化结果Fig. 5 Topology optimization results
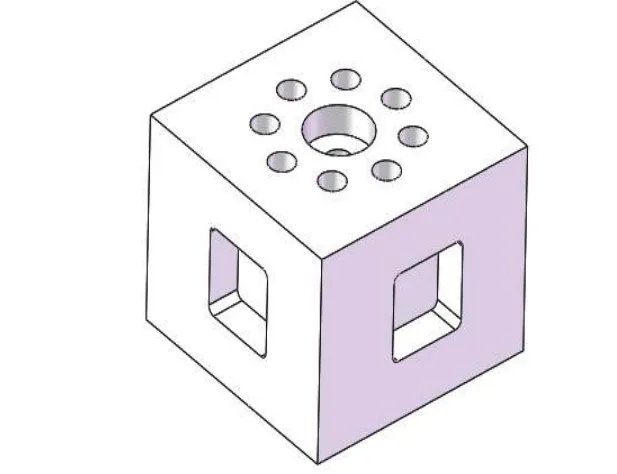
图6 改进后母夹具结构Fig. 6 Structure of improved master fixture
拓扑优化后的夹具模态仿真计算的前4 阶频率分别为3904.0、3904.4、4282.9 和8405.7 Hz,优化后模型质量为10.36 kg。
3.2 尺寸优化
经拓扑优化后夹具基本形状己经确定,母夹具的一阶固有频率已远超2000 Hz,但夹具质量仍相对较大。在确保夹具一阶固有频率的基础上,对其进行结构尺寸优化,以进一步提高其固有频率并降低夹具质量。
结构尺寸优化是一个多目标优化问题[16-18],最优解一般称作Pareto 最优解[19]。基于Pareto 排序的多目标遗传算法的特点是利用各代间包含潜在解的种群,进行多向性和全局性的搜索,这是求解Pareto 最优解集的一种有效手段[20,21]。为了使振动夹具的一阶固有频率达到最优,质量最轻,本优化中采用ANSYS Workbench 软件中基于多目标遗传算法(MOGA)的尺寸参数优化方法进行优化。以母夹具的长、宽、高度,侧面凹槽的宽、深度,以及中间圆形凹槽的直径、深度共7 个尺寸作为优化参数。以振动台动圈尺寸以及子夹具外形尺寸作为母夹具长、宽、高3 个参数的约束条件,并根据夹具结构大小设置侧面凹槽及中间圆形凹槽的尺寸约束条件,以夹具一阶固有频率最大化以及夹具质量最小化为优化目标进行优化设计。尺寸优化约束条件及优化目标见表2。
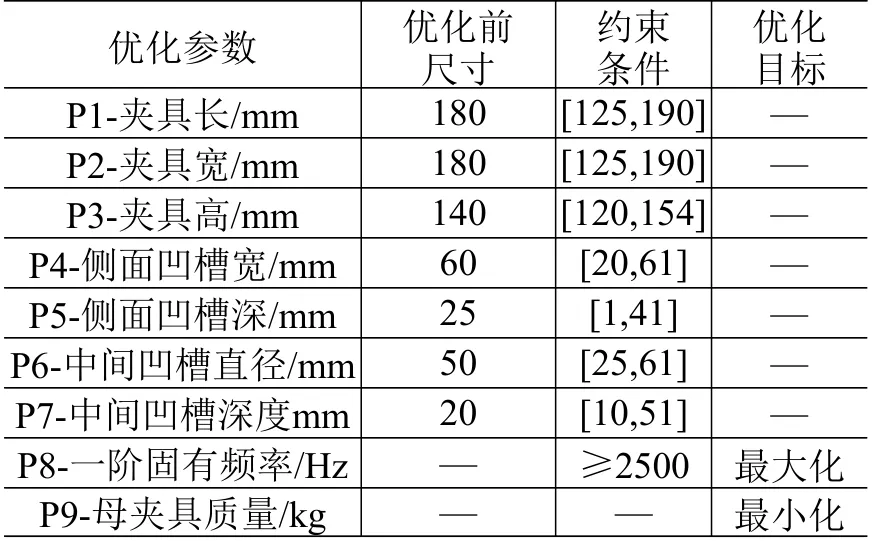
表2 尺寸优化约束条件及优化目标Table 2 Size optimization constraints and optimization goals
结构尺寸优化设计主要步骤如下:首先采用蒙特卡罗抽样技术进行设计参数样点的选取;其次,求解每个样点的响应结果,借助二次插值函数完成设计空间响应面的建立;最后,借助响应面分析结果实现多目标遗传算法优化分析,得到一组不同的Pareto 最优解集,并按照需求选择其中一个最优解作为优化方案。
结构尺寸参数优化试验设计采用默认的中心符合设计法,自动生成79 组设计样点。对79 组样点进行计算,形成响应面结果,如图7 中所示,可以看出两个目标参数的设计点均非常接近对角线,说明拟合程度较好。利用多目标遗传算法,在响应面上实施优化,收敛准则如下:在本次迭代过程中,当有70%的样本分布在Pareto 优化前沿时,迭代结束。其中,种群总数设置为1000 个,最大迭代次数设置为100。

图7 响应面拟合度离散图Fig. 7 Discretization of fitting degree of the response surface
本优化中,夹具的一阶固有频率与质量同样重要,因此在目标函数的重要性(importance)中将两个设计目标的重要性设置为默认值(Default),则两个目标值的权重值各取0.5。
结构尺寸参数优化得到3 个优化方案,它们的一阶频率均远高于试验最高频率2000 Hz,选择优化方案中质量最小的一组作为最优解。
考虑到方便机械加工,对最优解的尺寸进行圆整,重新进行三维建模并计算母夹具模态。结构模型随优化设计变化的过程如图8 所示,优化前后尺寸参数对比见表3。母夹具优化后的一阶固有频率为3903.4 Hz,远超2000 Hz,较拓扑优化前提高1217 Hz,提高了45.3%;优化后质量为4.00 kg,较优化前降低16.49 kg,降低了80.5%。
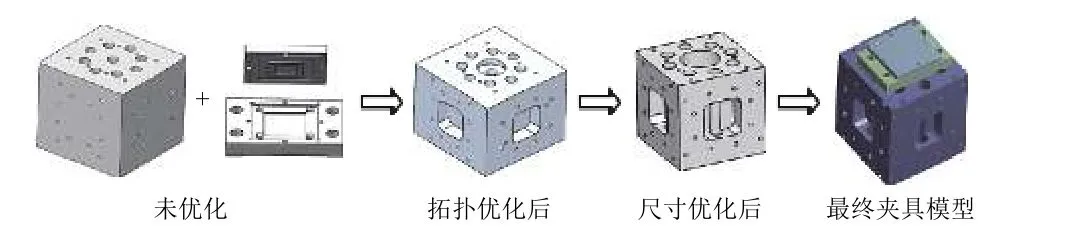
图8 优化过程夹具模型结构变化Fig. 8 Structural optimizations of the fixture model
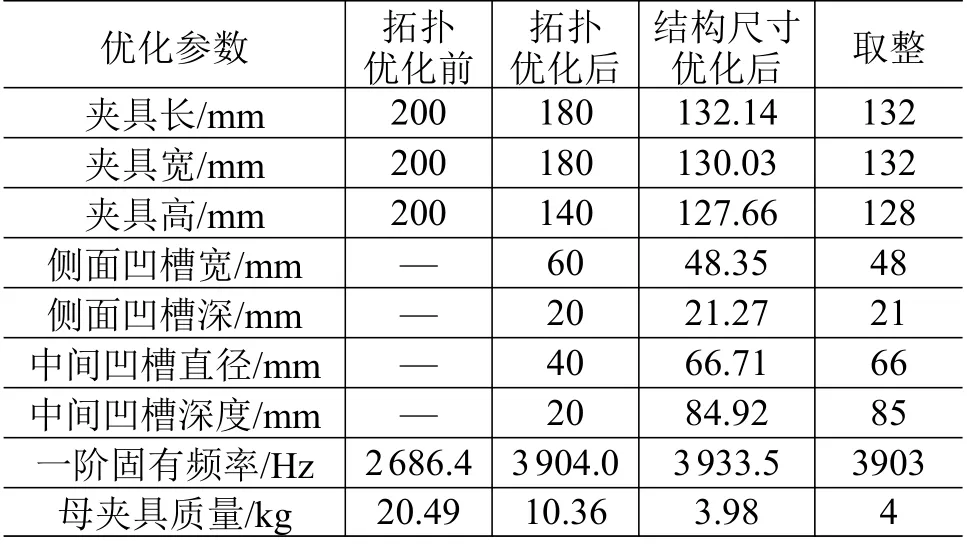
表3 母夹具优化前后尺寸参数对比Table 3 Comparison of dimensional parameters of the master fixture before and after optimization
将优化后的夹具装配体进行模态仿真分析,结果如图9 所示,其前4 阶模态分析结果分别为3 087.3、3 210.3、4 283.6、5 797.5 Hz。仿真结果表明优化后的夹具的固有频率及质量均满足设计要求。
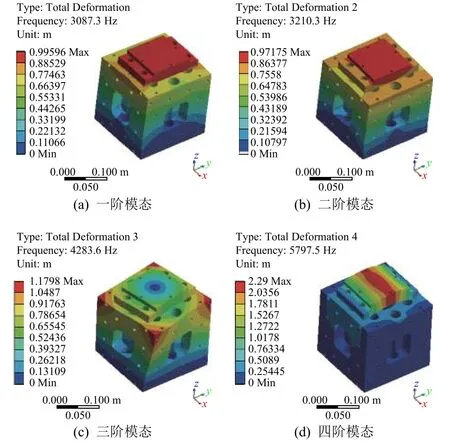
图9 优化后夹具装配体前四阶模态Fig. 9 The first to the fourth modes of the fixture assembly after optimization
4 优化结果验证
4.1 响应仿真分析
模态分析只能提取到夹具的模态频率和阵型,可以初步判定夹具设计的合理性,但无法得知夹具在振动工况下的具体响应情况,因此还需要对夹具进行随机振动以及扫频振动响应分析,得到夹具在振动下的响应情况。
随机振动分析步骤为:建模→获得模态解→转换成谱分析类型→定义和施加功率谱密度激励→求解→查看结果。
扫频振动分析步骤为:建模→获得模态解→转换成谐响应分析类型→定义和施加加速度激励→求解→查看结果。
本次仿真是在夹具安装状态下,选取垂直于振动台台面的激励方向,取子夹具盖板中间点的振动响应进行分析。
施加的随机振动激励如表4 所示。

表4 随机振动输入激励Table 4 Input excitation of random vibrations
随机振动加速度响应结果如图10 所示,可见,功率谱密度最大为20.579 (m/s2)2/Hz,与输入激励偏差+0.12 dB,符合夹具设计要求。
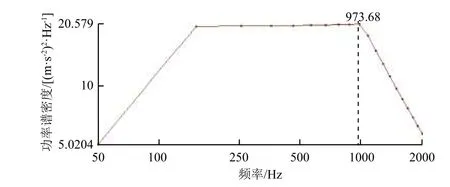
图10 随机振动响应分析结果Fig. 10 Random vibration response analysis results
施加扫频振动激励如图11 所示,加速度响应结果如图12 所示。可见,夹具扫频振动分析结果中响应加速度与输入激励信号幅值并无明显变化,扫频加速度响应值稳定在196 m/s2,符合±20%的响应范围要求。
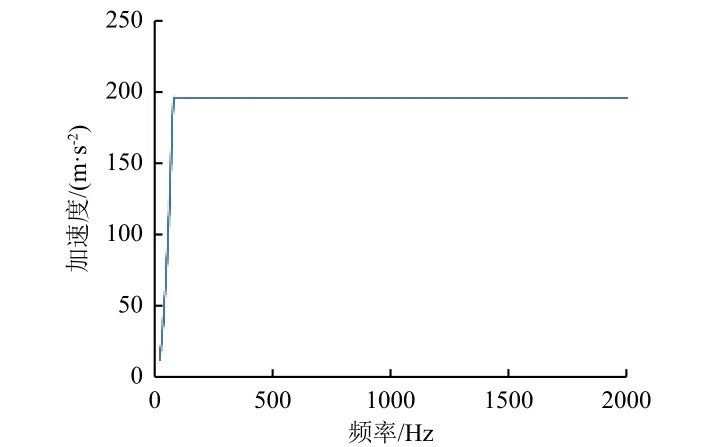
图11 扫频振动输入激励曲线Fig. 11 Input excitation curve of sweep frequency vibration

图12 扫频振动响应分析结果Fig. 12 Analysis results of response of sweep frequency vibration
4.2 试验验证
在确保夹具一阶固有频率、质量以及传递响应均符合要求后,加工夹具并对其进行试验验证,主要测试按标准要求的振动输入激励下夹具的加速度响应是否符合设计要求。如图13 所示,夹具实物质量与仿真结果相差较小,在振动台动圈以及子夹具盖板上各安装1 个加速度传感器,动圈上传感器作为振动激励输入控制传感器,子夹具盖板上传感器作为响应监测传感器。结果见图14 和图15,其中,黑色曲线为激励输入,紫色曲线为监测的响应。可见:集成电路振动夹具在2000 Hz 试验范围内扫频无共振,夹具处加速度响应在±5%内;随机振动功率谱密度响应偏差在±1.5 dB 内。结果表明夹具设计符合要求。

图13 夹具装配实物Fig. 13 The fixture assembly
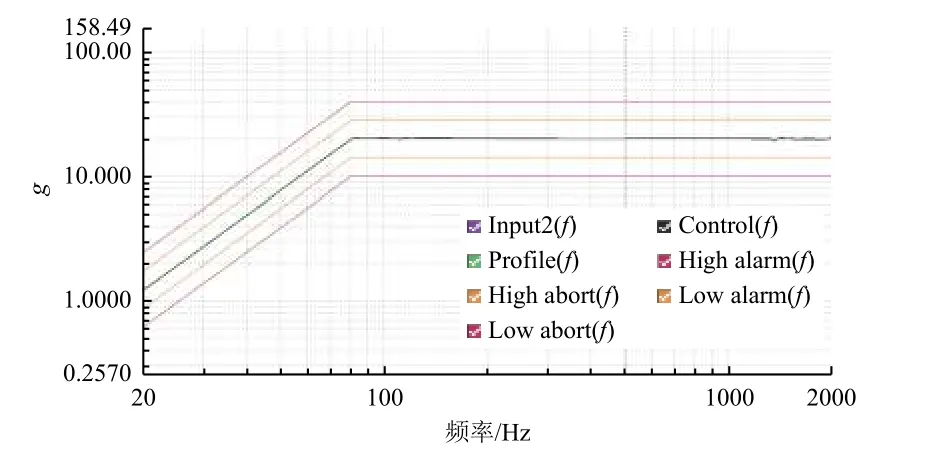
图14 夹具正弦振动响应测试Fig. 14 Sinusoidal vibration response test for validation of the fixture

图15 夹具随机振动响应Fig. 15 Random vibration response for validation of the fixture
5 结束语
本文以某型航空航天用CQFP228 封装复杂集成电路为例,针对航空航天严酷的振动试验条件以及复杂封装结构难以刚性固定的特性,采用基于拓扑优化和多目标遗传算法的振动夹具优化设计方法,对夹具结构的固有频率以及质量进行优化,并对夹具模型进行扫频振动、随机振动试验响应仿真分析,最后对夹具装配实物进行了测试,验证了夹具的设计、优化方法的合理性及有效性。该算例中振动夹具一阶固有频率较优化前提高了45.3%,质量较优化前减小80.5%,扫频振动以及随机振动响应均符合标准要求。
本文设计方法有效解决了以往采用经验或仅用单一尺寸优化设计的复杂集成电路振动夹具可能出现的固有频率低、振动加速度响应均匀性差和夹具质量过大等常见问题,对航空航天用复杂集成电路振动夹具的设计和改进具有参考价值。

