基于数据驱动的电动汽车充电站选址布局研究

杨晓东 马洪恩 王宁 许可

（1.杭州微联智控科技有限公司，杭州311100；2.同济大学 汽车学院，上海2018041）

主题词：电动汽车 充电桩 选址 贪心算法 P中值模型

EV Electric Vehicle

SOC State Of Charge

NCBDC National College Big Data Competition

全国高校新能源汽车大数据创新创业大赛

NP Non-deterministic Polynomial

0 前言

我国目前已经是全球充电设施网络规模最大的国家。尽管如此，截至2020年6月，我国新能源汽车市场保有量为417万辆，就此数据对比来看，车桩比为3.1∶1，车桩比仍较为悬殊。随着未来中国新能源电动汽车产业的发展，新能源汽车的增长速度将会更快，到2030年，我国新能源汽车数量预计要达到6 000万辆，于此同时车桩比也要进一步降低，未来十年，我国充电桩的缺口还会更大。

随着电池技术的发展，新兴的新能源造车势力的兴起，传统车企在新能源研发和建设方面逐渐加大投入，以及国家对新能源车的各种优惠政策的加持，目前新能源汽车正在逐渐走向成熟。充电基础设施作为保障电动汽车可以大规模使用的配套基础设施，将很大程度上影响和制约着整个电动汽车行业的发展和电动汽车车主的用户满意度。因此，一个城市电动汽车能否充分普及和应用与城市是否提前对充电站的布局进行了科学合理的规划息息相关。

由此可见，对充电桩的建设进行合理规划将是每个城市在发展新能源汽车时所必须要研究的一个课题。如果建设的前期缺乏有必要的规划，只是盲目地追求充电桩的数量、充电站的规模，必然会造成充电桩得不到充分利用的资源浪费问题以及公共充电站覆盖范围重复的问题。所以，各大城市在建设充电基础设施之初，必须要充分考虑到电动汽车的数量、电动汽车的时空分布情况、用户的用车出行习惯方面因素，才能对充电设施的建设做出科学合理的优化。做到既可以满足未来电动汽车数量增长而产生的充电需求的同时，又不会使充电设施大量浪费。

因此本文从满足用户充电需求的角度出发，利用P中值模型和贪心算法来进行电动汽车充电站选址布局。利用此方法，既可以满足用户的充电需求，又能使公共充电设施得到合理的优化配置。于此同时，由于电动汽车的充电功率远高于一般家用电器的使用功率，在进行充电基础设施建设之前应当与当地的电力公司、国家电网等充分沟通、相互协调，将充电桩与充电站的建设有效地纳入到城市电网的发展规划中。只有城市电网与充电桩充分的相互协调与配合，才能使充电设施有可靠的电力供应，才会使城市电网能够安全平稳的运行。因此本论文所讨论的对规划选址问题的研究十分必要。

1 出行实时数据处理

本文所用数据为2020年NCBDC大赛提供的2019年10月-12月，北京市87辆纯电动私人乘用车的运行数据。

科学合理的对新能源乘用车充电需求进行测算，是确保充电桩“新基建”落地的关键因素。通过新能源汽车运行数据测算这些车辆的充电需求数据，对公共充电站选址定容具有重要意义。

数据的主要字段为车辆唯一编号、数据采集时间、车辆状态、充电状态、电池电量(State of Charge,）以及经纬度信息。字段说明如表1所示，其中每辆车都会有一个唯一的随即编号，车辆采集时间精确到秒，数据时间间隔以30 s居多，车辆状态中1表示启动，2表示熄火，3表示其它。充电状态中1表示停车充电，2表示行驶充电，3表示未充电状态，4表示充电完成。的范围为0%～100%，精度为1%。经纬度默认为东经、北纬。

表1 原始数据字段说明

利用以上数据，本案例从北京市政府角度出发，对即将发放的新能源小客车指标，提前进行充电基础设施的选址布局规划。本案例假设政府只能在提出申请加装充电桩的现有停车场的备选范围内，通过给予停车场经营者部分补贴的方式，对相应停车场进行充电基础设施的建设。因此，本文假设某月共56个停车场提出加装充电桩申请，政府需要根据其是否能满足用户充电需求为衡量指标，在这56个停车场中选出部分停车场给予补贴，从而对充电站的建设顺序进行一定的选择，防止出现建设过快和过慢现象的发生。本文所建充电站均为满足公共需求的充电站，如前所述，目前，公共充电站只是充当电动汽车临时充电的场所，因此用户对大充电功率要求较高，本文选址布局的充电站均可以满足这一趋势需求，并且假设充电站的建设对北京电网影响不大。

原始数据有大量的缺失和异常2种情况，包括数据值缺失、工况矛盾、车辆状态变化异常以及数据数值情况异常的情况。因此根据物理意义，本文数据清洗时，对部分可修复数据进行了修复。对于数据值缺失，比如一些车辆的充电状态数据有缺失，需要根据其的变化来对缺失值进行补充。如果上升，则将充电状态重新设置为1（停车充电），如果下降，则将充电状态重新设置为3（未充电状态）。对于工况矛盾这种情况，比如某辆车同时处于启动和停车充电两种状态时，可以根据前后时段的变化，来得到具体哪个值异常，并将其重置。对于车辆状态变化异常，有些车辆的车辆状态一直为熄火，但其经纬度会发生变化，于是便需要根据车辆经纬度变化情况，重新设置其车辆状态。对于数据数值情况异常情况，比如某辆车在短时间内突然增加到100%，或突然降为零，那么会判定该数据值异常，此时会根据其前后情况，插值得到此时刻的。

数据清洗结束后，与原始数据进行对比，发现原始数据中存在异常值的数据约占数据总数的25%，对其中64%的数据进行了重构与补充，修复了47%的异常数据。之后对原始数据汽车的充电片段进行累积，去除了3个月内累计充电时长小于1 h的10辆车。并删除相应数据，得到有效数据2 708 403条和有研究价值的车辆77辆。通过地图得到北京市的经纬度范围,即北京位于北纬39.5˚到41˚之间,东经115.5˚到117.5˚之间。因此对不在本文研究范围内的北京市以外区域的数据进行删除，最终得到2 414 754条在研究范围内的数据。

2 用户公共充电需求分析

通过对车辆充电状态进行筛选，得到各充电状态为1的点，并将其充电位置的经纬度在图中显示出来，便可得到该辆车日常充电的点的位置。

最终将763个不同经纬度的充电点聚合为267个充电桩。之后依据充电桩服务的车辆是否唯一，以及充电的时间是否规律，来判断这267个充电桩是私人桩还是公共充电桩。最终得到这些充电桩有49个私人桩，218个为公共桩。

对用户的充电习惯进行分析，即将每个用户的充电数据单独提取出来，得到用户每次充电的起始值。将每个用户充电的起始值从大到小排序，选取下四分之三位数作为此辆车充电的最低阈值。由于每辆车的电池容量以及车主的使用习惯不同，每辆车的充电最低阈值也各不相同，但其充电阈值均在20%到40%之间。由于本文所用数据车辆数量较少，采取一车一阈值的方式，以最大程度上保障需求的可靠性。

对数据中所给车辆的电池电量进行分析，发现样本中车辆电池电量平均值为45.06 kW·h，考虑到用户长时间使用车辆后电池会有一定的衰减，因此数据中每辆车可装载的最大电量平均为40 kW·h左右。通过对所有车辆信息进行统计，发现用户在3个月内的平均充电次数为24.73次。平均私家车用户每3到4天充一次电。数据中有私人桩的私家车为49辆，无固定充电桩的车辆为28辆。拥有私人充电桩与没有私人充电桩的比例为7：4。

对数据进一步研究发现，拥有私人充电桩的用户对公共充电需求较低，平均每月在外充电1次左右。拥有私人桩的车主在外充电主要原因是由于当日出行较远，其电池电量无法支撑其一整天的行程距离之和时才会选择在公共充电桩进行临时充电。通过对用户出行较远时行驶距离进行统计，发现当用户每日行程往返超过130 km时，认为此用户当日出行必有公共充电需求，这一数据可能会由于未来电池最大容量的提升而发生变化。

3 用户公共充电需求测算

上文已经将存在充电需求的点在地图上表示了出来，在这些点中，用其最终停车点表征其这段路上的需求。将离车辆自己家用充电桩附近的需求点去掉，即可得到这辆车的真实公共充电需求点的分布。由于电动汽车车主充电行为随机性很强，而以往的研究将充电概率设为一个固定的常数，这样的做法有些主观，不够准确。本文考虑了电动汽车当前的荷电状态与车主下一次行驶里程这两个主要因素，将上文提到的各个需求点建立了一个充电概率计算模型，作为该需求点的权重。概率模型公式为：

式（1）中：P、P分别表示当前电动汽车的电池荷电状态与下一段行驶里程对充电概率的影响；表示电动汽车电池荷电状态的最小阈值； 表示电池容量；ω表示每公里耗电量；表示下一段行驶里程；、为影响因子。

本文假设电动汽车的当前电量如果不足以支撑其下一次出行，那么电动汽车车主必定选择充电，并且为了安全性，电动汽车的需要有一定的阈值。所以，当电动汽车满足上述假设条件时，车主充电概率为1。

对于下一行驶目的地，可以根据下次车辆状态为熄火的地点来判定。众所周知，电动汽车当前越低，下一次行驶里程越高，充电概率越高。基于这一规律，考虑不同影响因素建立出的概率计算公式见式（2）。

电动汽车当前对电动汽车充电概率影响具体计算公式如式（2）所示：

下一次行驶里程对电动汽车充电概率影响具体计算公式如式（3）所示。

式（3）中：与为根据北京市地图确定为5和105。本文引入、两个参数作为影响因子，代表电动汽车当前与下一次行驶里程这两个因素所占的权重，本文认为电动汽车的当前对电动汽车是否进行充电影响较大，因此，取：=0.65，=0.35。将式（2）与式（3）代入式（1）中，便可以得到电动汽车充电概率计算模型。

通过概率公式得到各点的需求概率作为权重，赋予每个需求点。

将需求点在地图上（基于百度folium地图生成器，图1～5）显示出来，需求点的散点图、热力图和聚类数字图如图1、2、3所示。

图1 充电需求点散点图

图2 充电需求热力图

4 选址模型

考虑到本文所用数据类型为汽车经纬度点，以及上文所得到的需求为点需求，所以决定用P中值模型作为本文的充电站选址模型。考虑到目前北京市的房价和地价，以及土地利用率，得出北京市市中心目前很难会再有空地来单独建设充电站，因此目前充电桩的建设将以在现有停车场上加装充电桩为主。在北京市发展和改革委员会官方网站上得到拟申请市政府固定资产投资补助的公用充电桩项目清单，找到其经纬度点，作为P中值模型中的候选点集合，并将各停车场位置在图中标识出来，如图4所示，备选停车场集合为图中蓝色点。将充电需求点为作为客户，以备选停车场集合作为服务点，从而构造出从需求点到备选停车场距离之和最短的P中值模型。

图3 充电需求点聚类数字图

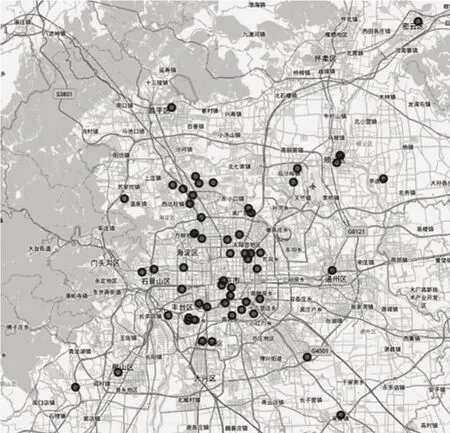
图4 备选停车场位置

当充电需求点与备选停车场个数较大时，P中值模型具有组合爆炸的特点，因此P中值模型是NP难题。由于本文所用数据遍布北京市，范围较大，因此选用贪心算法进行求解。

贪心算法并不一味地追求最优解，只需从众多解中得到一个较为满意的解即可。在算法设计时，首先要明确目标函数和优化条件，并制定一个可行的贪心准则。之后并不需要列举所有情况，而是以当前情况为最优解，利用制定的贪心准则，一步步往下搜索，直到找到满足该问题的目标值。贪心算法具有步骤相对简单，计算量较小、节约时间的优点，因此在解决NP难题以及具体的选址问题中得到了广泛应用。

基本步骤如下：

（1）令当前选中设施点数=56，也就是将所有56个候选停车场全部都选中；

（2）求出各个需求点到离其最近的停车场的距离，并乘以各需求点的权重，计算出总距离；

（3）将56个设施候选点从候选集中每次取出一个，比较这56种情况下的总距离，找出总距离增量最小的停车场，将其从候选集中去除。

依此类推，当k值减少到P时，得到的即为最能满足公共充电需求的站点。通过对总距离增量的分析，发现P值在15左右增长迅速，结合前文对充电站规模的测算，P值选为15左右也较为合理。最终选址15作为本文模型的P值。

最终将选择的15个停车场在地图上显示出来，如图5所示，最终得到备选点为图5中圆环点所示，浅色点为需求点，深色点为未被选中的停车场。

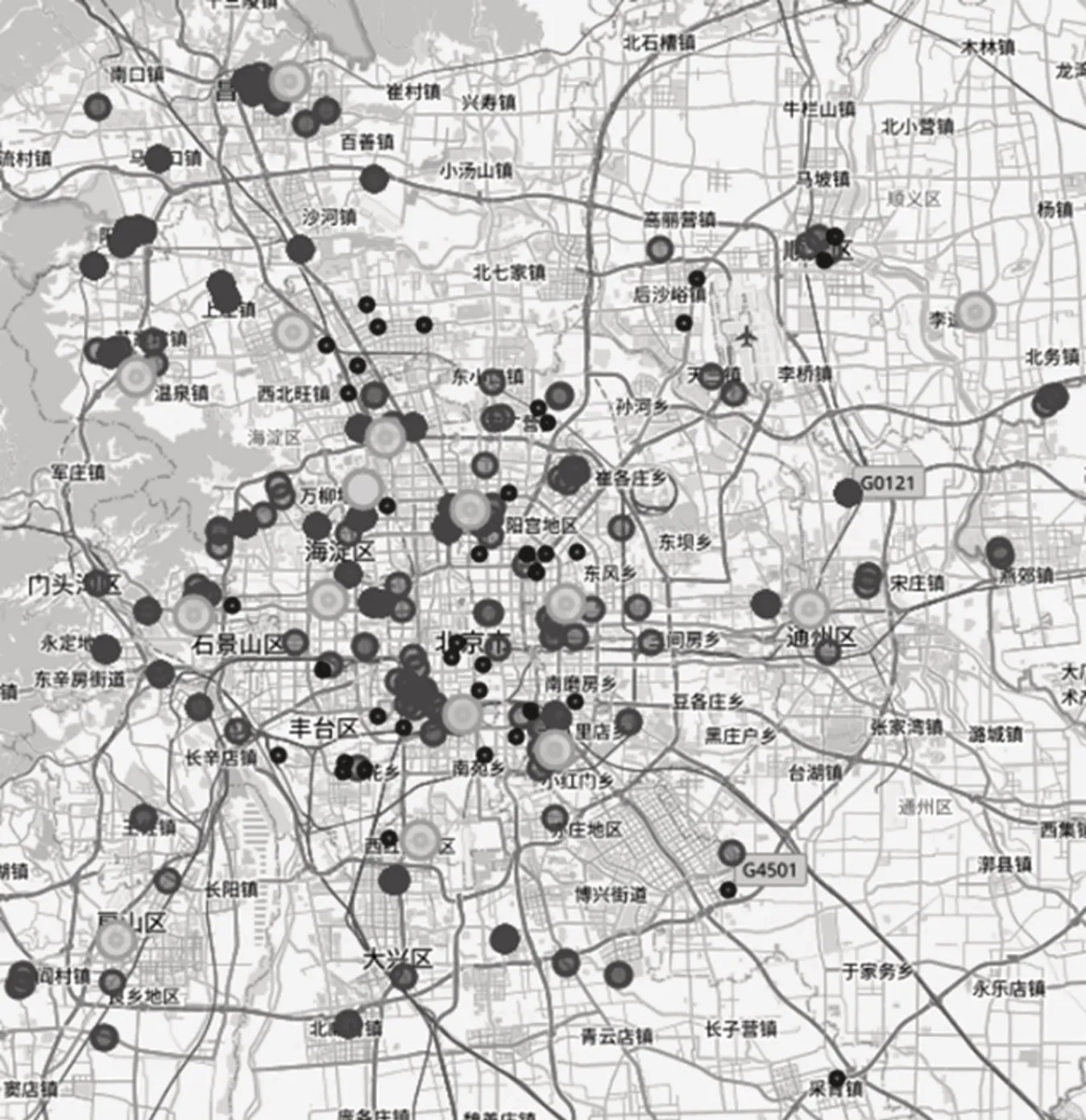
图5 最终选定停车场位置

5 结论与展望

通过研究发现，采用需求点的测算方式在测算纯电动汽车充电需求时可以有一定作用，可以对需求做出合理的测算。另外，以往的研究将充电概率设为一个固定的常数，这样的做法有些主观，不够准确。通过考虑电动汽车当前的荷电状态（）与车主下一次行驶里程这两个主要因素，结合点需求与出行链需求，将各个需求点建立了一个充电概率计算模型，这样的需求测算更加科学合理。在选址模型上，P中值模型在解决从备选点中选出服务点的这类选址问题中优势明显。最终提出了一种将电动汽车用户需求与电动汽车充电概率模型相结合的充电站选址方法，并采用贪心算法得到了最终选址方案。此方法不仅可以确定最终的选址方案，还可以为各个候选点进行排序。

由于本文采用数据驱动的方式，从真实数据出发，通过对北京市充电基础设施相关问题的调研，并结合北京市实际停车场的位置确定最终选址方案。因此，得到了一系列选址布局优化建议与选址方法，可以指导未来北京市及其它城市的充电站建设。同时此方法的数据处理方式、研究模型与方法也具有充分的扩展性，只要给定设施候选点，便可得到最为满足需求的选址位置，并可对各个充电站选址位置进行排序，可直接移植到更大数据量的选址问题中。

但是，由于用户的充电行为具有一定的主观性，需求测算模型考虑因素还不够全面。后期可增加测算模型因素，如：充电站的建设成本以及充电站建设对电网的影响、分时定价方案对于用户充电需求的影响等，并对各类参数进行回归分析，进行准确程度验证，提升数据真实性。另外，本文充电桩样本数较少，只是使用了北京市77辆车所用的充电桩数据，未来可以拓展数据量。相关数据由于受到限制的原因，无法进行深入分析。未来可以将更多影响充电站建设的因素加入到需求测算与选址模型中，使模型更加科学合理。