城际铁路预应力混凝土简支箱梁梁端局部应力分析

张磊

（中国铁路设计集团有限公司土建设计研究院，天津 300308）

1 引言

预应力混凝土简支箱梁截面由于结构简单、受力性能良好、施工方便，已在我国城际铁路桥梁建设中被广泛应用[1]。但是，箱型截面力学特性不够明确，尤其是梁端锚固区，受力更为复杂。锚下混凝土承受经锚具及垫板传递而来的端部预压力，处于三维空间应力状态，在预应力筋张拉后可能产生较大的局部压应力和横向（与荷载轴线垂直的方向）拉应力[2]，导致混凝土产生压碎或者拉裂破坏，影响预应力的有效传递，从而降低结构的安全性和耐久性[3]。同时，大吨位预应力体系的应用促进了桥梁轻型化的同时，也进一步加剧了梁端局部应力大、容易开裂的问题，这种情况在预应力混凝土大跨度简支箱梁中尤为突出[4]。因此，开展城际铁路预应力混凝土简支箱梁的力学特性分析，深入研究梁端锚固区局部应力水平显得尤为必要。

针对预应力混凝土简支箱梁的端部应力问题，很多学者开展了研究工作。李瑞林[5]基于有限元对预应力梁梁端局部应力进行了分析，阐述了端部应力集中引起锚下劈裂区和锚间剥离区的机理；白鸿国[6]利用ALGOR 软件计算分析了秦沈线32 m 双线整孔箱梁端部的应力分布情况，提出了梁体端部横向拉应力的改善方法；潘春风[7]分析指出预应力梁端块局部承压、预应力梁端块的横向拉力、预应力传递长度，是梁端锚固区的主要问题；薛洪卫[8]针对32 m 高速铁路简支梁结构进行分析，提出了支座纵向布置的方案优化；何旭辉[9]针对T 型梁锚固区布置，对梁端局部应力的影响开展了研究，指出支承中心线与端部的距离，钢筋的弯起角度以及梁端锚具的分布对梁端应力影响较大；陈艳[10]针对大跨度预应力混凝土连续梁端部预应力锚固区，基于Ansys 软件建立了精细化的有限元模型，分析了端部阶段的局部应力，阐述了锚垫板周围产生较大的拉应力的机理；王树平[11]建立了32 m 预应力铁路简支箱梁的三维有限元精细化模型，改变槽口半径，对该桥进行了锚固端局部应力分析。结果表明，随着槽口半径的增大，锚穴及检查孔槽口倒角处混凝土的拉应力先增大，再降低，再增大的趋势。

上述研究主要针对高速铁路桥梁开展的，目前对于城际铁路预应力简支箱梁的梁端应力研究仍较为少见。因此，本文拟基于有限元方法，建立精细化的整梁实体分析模型，采用实体单元模拟混凝土主梁、锚垫板，采用壳单元模拟支座钢垫板，采用杆单元模拟预应力钢筋。通过自由度耦合模拟混凝土主梁与预应力钢筋之间的连接，通过共节点模拟支座钢垫板、锚垫板与主梁之间的连接。基于该模型，在ZC 荷载（中国城际轨道交通活载）作用下对梁端局部应力进行分析，为设计提供一定的参考。

2 箱梁概况

以时速200 km 的城际铁路32 m 双线简支箱梁（2.3 m 梁高）为例，其设计最高行车速度为200 km/h，上铺双块式双线无砟轨道，正线线间距为4.2 m，适用于直、曲线段落，最小曲线半径为2 200 m，困难时可为2 000 m，活载类型为ZC 荷载。

2.1 几何尺寸

梁部基本信息如下：

1）截面类型为单箱单室等高度简支箱梁，梁端顶板、底板及腹板局部向内侧加厚；

2）桥面宽度：防护墙内侧净宽8.0 m，桥梁宽10.6 m，桥梁建筑总宽10.95 m；

3）梁长为32.6 m，计算跨度为31.5 m，横桥向支座中心距为4.1 m，箱梁梁体中心线处高度为2.30 m，支座中心线至梁端0.55 m。

2.2 梁端布置

梁端预应力钢束布置基本信息为：

1）底板中央开设1 700 mm×250 mm×550 mm（横向×纵向×竖向）的进人洞，洞内布置1 根N1a、2 根N1b 共3 根钢束（均为14-7φ5 mm），底板进人洞外布置2 根N2a、2 根N2b 共4 根钢束（均为14-7φ5 mm）；

2）腹板布置N3～N7 各2 根共10 根钢束（均为15-7φ5 mm），相邻两束预应力钢筋间的竖向间距分别为300 mm、400 mm、300 mm、400 mm；

3）支座横向间距4.1 m，腹板束及底板束布置避开了支座上座板预埋件。腹板与底板交接处的倒角半径为300 mm。

梁端预应力钢束布置如图1、图2 所示。

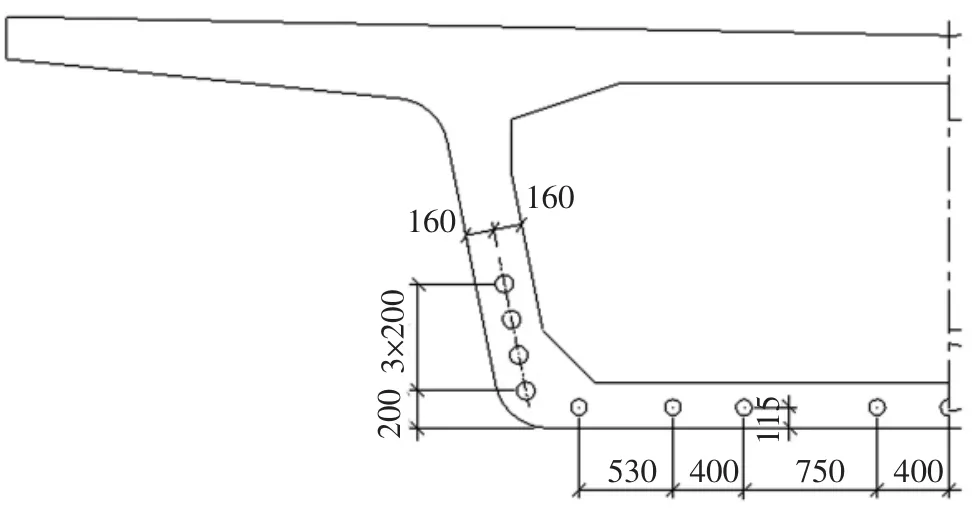
图1 梁端预应力钢束布置一

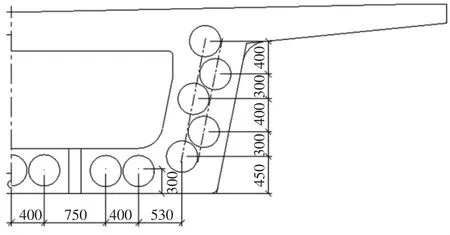
图2 梁端预应力钢束布置二

3 有限元分析模型

3.1 模拟方法

基于Ansys 软件建立有限元模型，其中，混凝土主梁采用实体单元模拟（SOILD45），共93 592 个单元，26 438 个节点；支座钢垫板采用实体单元（SOILD 45）模拟，共344 个单元，156 个节点；钢筋采用杆单元（LINK180）模拟，共630 个单元，647 个节点；锚垫板采用板单元（SHELL181）模拟，共2 824 个单元，1 854 个节点。

混凝土主梁与预应力钢筋之间通过自由度耦合的方式进行连接，支座钢垫板、锚垫板与主梁之间均通过共节点的方式进行连接。混凝土主梁有限元模型如图3 所示，预应力钢筋有限元模型如图4 所示。

图3 混凝土主梁有限元模型

图4 预应力钢筋有限元模型

3.2 模型验证

为验证模型的正确性，以支座反力、预拱度（扣除自重影响）、静活载挠度和竖向基频为例，将有限元模型计算结果与设计指标的对比结果见表1。可以看出，各项指标的相对误差均在5%以内，模型计算值与设计值吻合良好，表明有限元模型具有可靠性。

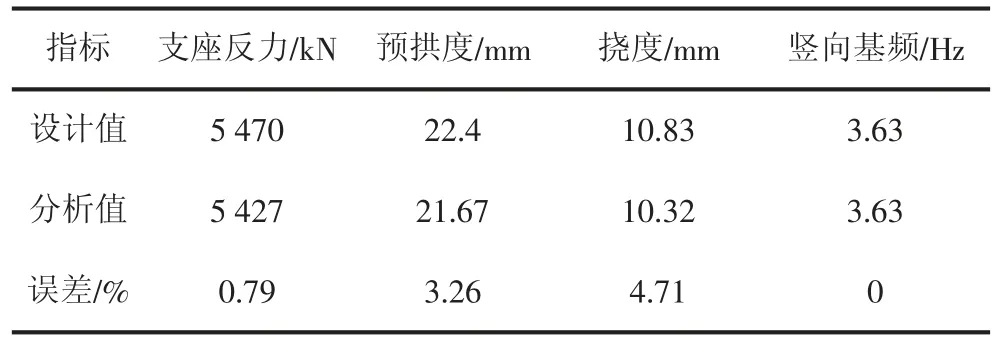
表1 有限元模型计算结果与设计指标对比结果

3.3 梁端应力分析

在上述有限元模型的基础上，考虑自重、二恒和预应力荷载，对整梁模型进行了静力分析，梁端应力云图如图5 所示。关注锚具孔外的主梁端部应力分布，可以看出，最大拉应力出现在梁端倒角处。虽然较大应力分布的区域较小，但是，最大应力高达4.94 MPa，与混凝土的抗拉极限强度较为接近，说明该处开裂风险较大，需对现有结构进一步优化。根据圣维南原理，锚具孔的直径约为0.4 m，距梁端0.55 m 处的剖面受力同样不利，取该剖面作为研究对象，其应力云图如图6 所示。可以看出，最大拉应力为1.29 MPa，最大压应力小于1 MPa，说明该处受力情况良好，混凝土不存在拉裂或者压碎破坏的可能。

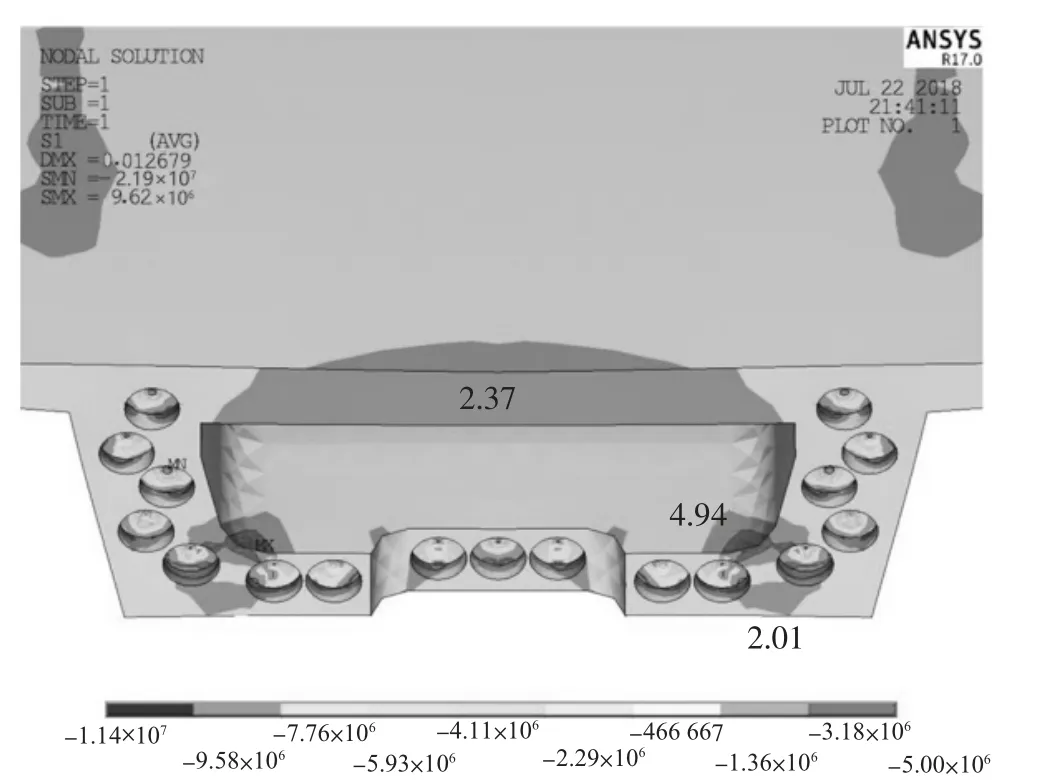
图5 梁端应力云图（单位：MPa）

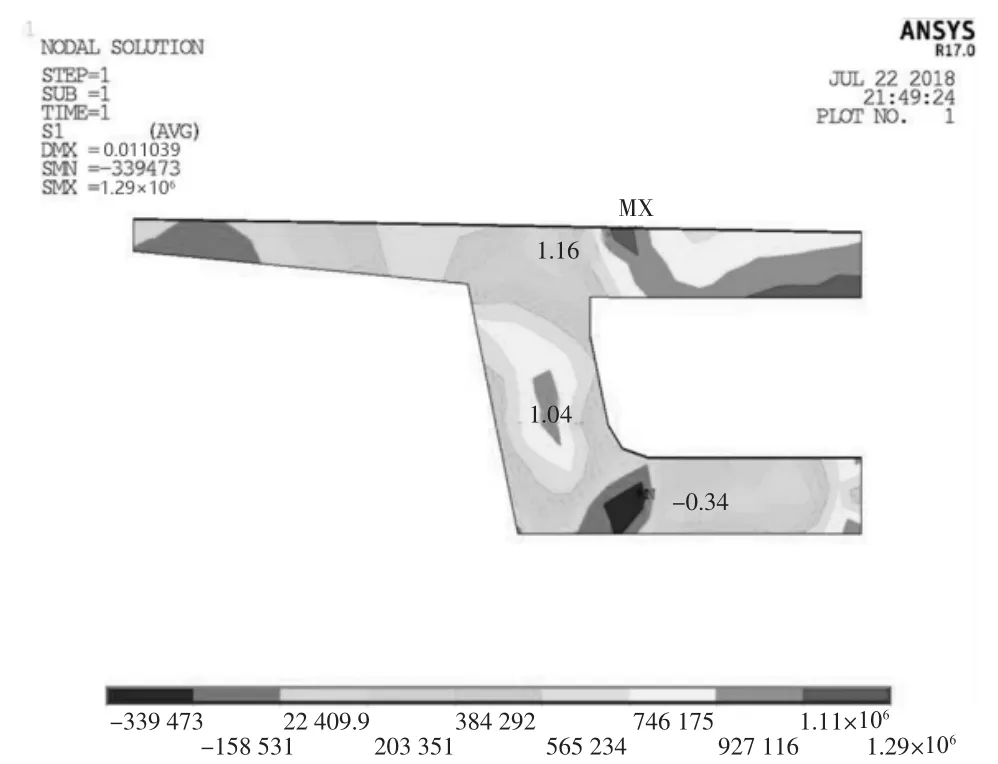
图6 0.55 m剖面应力云图（单位：MPa）

4 结论

本文针对城际铁路预应力简支箱梁，建立了精细化全梁实体有限元模型，选取挠度、基频等指标与设计值进行比较，验证了模型的正确性。基于该模型进行梁端应力分析，主要结论如下：

1）在自重、二恒和预应力荷载的共同作用下，底板倒角处为拉应力控制区，需要特别关注；

2）梁端倒角处最大拉应力与混凝土极限抗拉强度较为接近，存在开裂风险，需进一步优化设计；

3）距梁端0.55 m 处的剖面受力良好，不存在拉裂或者压碎破坏的可能。