基于Marmousi模型的CFS-NPML分数阶粘声波正演模拟

廖万平， 王兴建， 李卿武， 王崇名， 张俊杰

(1.成都理工大学 地球物理学院，成都 610059;2.油气藏地质及开发工程国家重点实验室(成都理工大学),成都 610059)

0 引言

地震波场正演模拟是预先构建数学模型或实体模型，然后通过研究地震波在模型中的传播规律与实际地震勘探资料进行对比，通过不断修正模型尽可能使模拟数据达到与探测资料接近，以至于能够更精确更高效地推断地下地层情况。但是在数值模拟常会遇到一个问题，在有界区域内模拟声波的传播，如果强行加截断边界，会导致虚假反射现象[1]，因此为了在有限区域内达到声波正演模拟的真实效果，需要一种反射非常小甚至不产生反射的人工吸收边界条件[2]。

目前已有许多方法，用以消除边界反射。Cerjan等[3]通过在计算机边界引入损耗介质来衰减向外传播的波，虽然取得了一定吸收效果，但是其对大角度边界反射吸收方面却不尽人意；Clayton[4]吸收边界在旁轴近似理论的基础上导出，但是其在特定的入射角和频率范围内，才具有较好的吸收效果；Liao Z P[5]基于牛顿后向差分公式推广了多次透射理论，应用平面波原理及二次插值方法的到，其实现简单，且精度能够很好的满足大多数工程计算，然而其吸收边界条件的不稳定性限制了其应用；Bérenger[6]提出了一种相对于传统吸收边界更高效的PML边界条件，其能够吸收来自各个方向、各种频率的波，而不产生任何反射，但随着对边界的研究和应用的不断深入，学者们发现当入射波传播方向于PML区域和内部区域接近平行时会导致其无法对高角度入射波/掠射波以及瞬逝波完全吸收。随着简单高效的CFS-NPML技术提出，其不仅解决了分裂场引起的数值误差，还提高了对高角度入射波/掠射波和瞬逝波的吸收效果，使得边界条件达到满足实际生产的要求[7]。CFS-NPML吸收边界的优越性其已被广泛应用于电磁波、地震波等波的传播数值模拟问题中，尤其是在地震波正演模拟领域，均获得了丰硕的研究成果。但是到目前为止鲜有基于CFS-NPML吸收边界在分数阶粘声波方面的应用。

这里以粘声波动方程的速度-应力方程为基础，完成了对C-E吸收边界、廖氏吸收边界、PML吸收边界、CFS-NPML吸收边界在均匀介质下的对比，然后更进一步将PML吸收边界和CFS-NPML吸收边界应用到分数阶粘声[9]条件下，并采用较为复杂的Marmousi模型进行数值模拟。结果表明与传统方法PML边界条件相比，CFS-NPML吸收边界具有更好的鲁棒性、可行性以及吸收效果，并且能够直观高效地反映声波在粘性介质中的传播衰减规律。

1 方法与原理

1.1 分数阶粘声波动方程

分数阶粘声波动方程描述的是声波在粘性介质中的传播规律由Kjartansson[9]提出。声波在二维均匀介质中传播时的质点运动平衡方程为式(1)。

(1)

式中：p为声压；ux和uz分别为质点在x、z轴方向的位移分量。

根据Caputo[10]分数阶导数定义,线性黏弹性介质中本构关系的褶积形式可转化为乘积形式，即

(2)

结合式(1)、式(2)和应变-位移关系(几何方程)可得式(3)。

(3)

根据式(1)、式(2)可推导出常Q衰减介质的声波速度-应力方程为式(4)。

(4)

式中：vx、vz表示质点在x、z轴方向的振动速度；D1-2γ为时间1-2γ的阶导数。

声波相速度频散关系和衰减系数分别为：

(5)

(6)

式中：cp为相速度；α为衰减系数。可以看出，两者均与频率有关：前者表明常Q衰减介质中波的传播速度是频率的函数，即存在频散现象；后者说明介质对地震波能量吸收有频率选择性。

1.2 完全匹配层(PML)

完全吸收边界条件思想就是在需要计算场值区域内采用速度-应力方程，在计算区域外使用一定厚度的截断边界，当波场运动到边界时，不会发生反射，而是穿过边界，在边界区域内场值按指数方式衰减，达到消弱边界反射的效果。在PML吸收层区域内，对频率空间域的x和z方向偏导分别作如下替换：

(7)

式中：ω为角频率；dx和dz分别表示为和方向的阻尼因子。

在PML边界条件应用时选择合适的衰减系数极为重要，选择不当会导致严重的边界反射现象。因此为达到降低反射现象的最佳效果，笔者采用Collino等[12]提出的一种PML边界与内部计算区域截断边界距离为指数关系的一种衰减函数：

(8)

式中：L为PML边界层的厚度；r为离PML层内边界的距离；Vmax为最大纵波度；Δγ为空间步长；R为理论反射系数。

1.3 非分裂复频移完全匹配层(CFS-NPML)

PML边界条件经过一般性推导将时间域变换导频率域，通过引入复伸展坐标。在频率域中复伸展坐标可以表示为式(9)与式(10)。

(9)

(10)

对式(9)、式(10)式引入复频移伸展(CFS)函数。其形式为式(11)。

(11)

式中：γ和α为复频移伸展函数中尺度因子和频移因子，满足γ≥1和α≥0。当这两参数同时取等号时就变为常规PML边界条件。参数γ主要对广角入射波/掠射波以及瞬逝波进行吸收。α主要对波的低频成分进行吸收，避免衰减系数出现奇异值。本文参数表达式如下

dθ(θ)=dmax(r/L)Pd

(12)

γθ(θ)=1+(Gmax-1)(r/L)Pk

(13)

αθ(θ)=Amax[1-(r/L)Pα]

(14)

(15)

式中：L为边界网格厚度；Pd、Pk、Pα为多项式衰减因子阶数，一般是在[1,4]之间，这里分别取2、3、1；Δγ为空间步长；vmax为最大纵波速度；r为层内点距边界与非边界的距离；Gmax通常介于1～20，这里取1；Amax=1.0*pi*f0，f0为震源主频；R为边界吸收系数，这里取0.000 1%；

1.4 吸收边界厚度优选分析

从图1给出的关系可以看出衰减项dθ(θ)、最大衰减项dmax的大小与吸收边界厚度成反比。由于边界的存在导致地震波传到边界时会产生反射波，而反射强度的大小取决于衰减项和最大衰减项的值[13]。当CFS-NPML层数减小时，衰减项、最大衰减项增大，导致数值反射强度增强，从而影响CFS-NPML吸收效果收衰减效果。由图1可以看出，当边界层厚度在20层到30层时曲线变化越来越小，越来越趋于平缓，综合边界条件的实用性和经济性考虑，即达到好的吸收衰减特征，同时减小数值反射波，CFS-NPML吸收边界选取20层～30层较为理想。

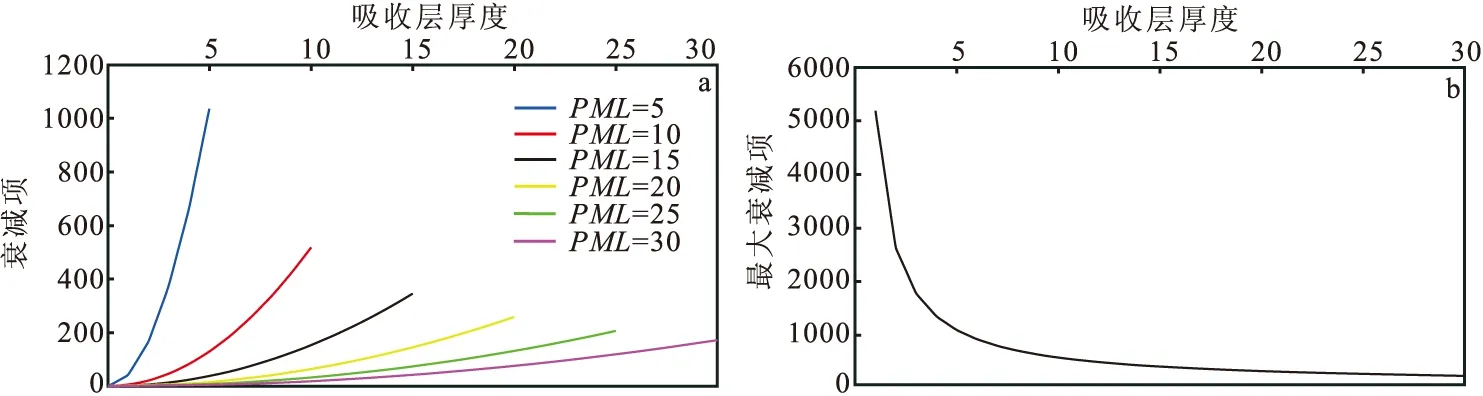
图1 吸收层厚度与衰减项、最大衰减项关系Fig.1 Relation between absorption layer thickness and attenuation term and maximum attenuation term(a)吸收层厚度与衰减项关系;(b)吸收层厚度与最大衰减项关系

2 数值算例

2.1 均匀介质模型

为了对比验证本文的CFS-NPML边界条件吸收效果和稳定性，图2、图3分别建立了C-E吸收边界、廖氏吸收边界、PML吸收边界、CFS-NPML吸收边界在均匀介质条件下的数值模拟和第200道波场记录。模型离散网格大小为400×300，空间网格采样步长X=Z=5 m，时间采样步长为0.000 1 s，震源位于(200,150)，震源采用30 Hz的雷克子波。由图2、图3可以明显看出C-E吸收边界能吸收大部分到达边界的声波，但还是存在小部分虚假反射。廖氏吸收边界能够较好吸收到达边界的声波，但仍然存在虚假反射现象。由于图3(c)和图3(d)采用更高效的PML吸收边界条件，因此其稳定性能和吸收效果均好于传统C-E吸收边界、廖氏吸收边界均未出现明显虚假反射现象。与PML边界条件相比CFS-NPML吸收边界在PML边界基础上加入了能够吸收广角入射波/掠射波以及瞬逝波和低频成分的吸收参数γ和α,能够有效吸收和压制反射波。从结果可以看出，经典PML边界到CFS-NPML边界吸收效果和正演模拟精度在不断提升。

图2 不同吸收边界在175 ms时刻波场快照Fig.2 Snapshot of the wave field at 175 ms at different absorption boundaries(a)C-E吸收边界;(b)廖氏吸收边界;(c)PML吸收边界;(d)CFS-NPML吸收边界

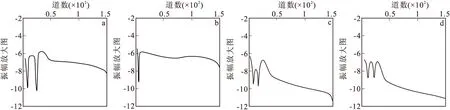
图3 不同吸收边界在175 ms时刻第200道记录Fig.3 Different absorption boundaries were recorded at the 200th track at 175 ms(a)C-E吸收边界波场记录;(b)廖氏吸收边界波场记录;(c)PML吸收边界波场记录;(d)CFS-NPML吸收边界波场记录

2.2 Marmousi正演模型

为了进一步对比PML吸收边界和CFS-NPML吸收边界的吸收效果，同时验证CFS-NPML边界吸收条件在分数阶粘声波正演模拟中的鲁棒性、可行性，笔者采用具有复杂地质构造和较强横向速度变化，且被广泛使用的标准Marmousi模型。参数模型见图4，模型是一个计算大小约为6.6 km×2.4 km的狭长区域，离散网格点为692×263，网格间距为dx=dx=10 m,震源采用零相位的雷克子波主频30 Hz，可使分辨率达到极限，采样点时间间隔为1 ms，震源位于(250,1)处，结合吸收效果及计算成本问题，作者选择边界上20层作为吸收区域，分别采用PML吸收边界和CFS-NPML吸收边界进行分数阶粘声波数值模拟，得到的地震记录如图5所示。

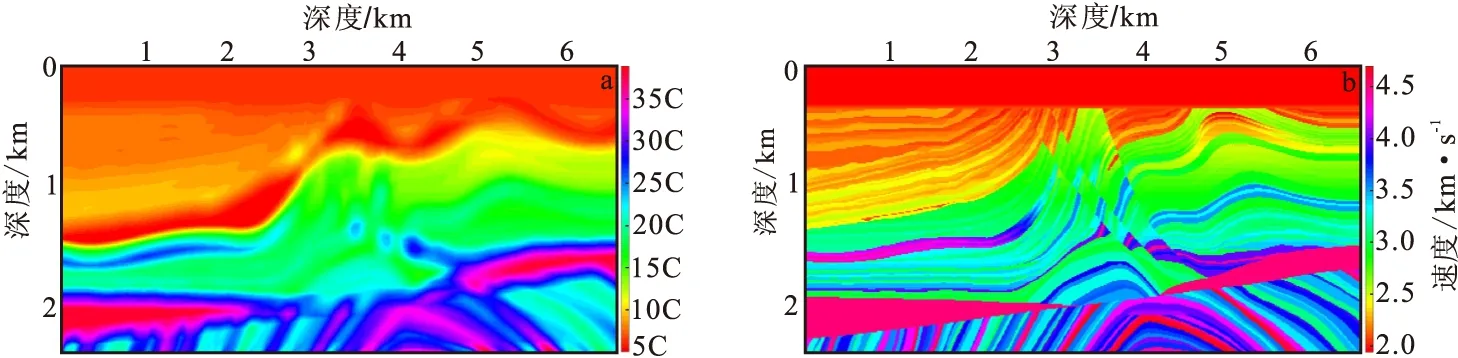
图4 Marmousi的衰减和速度模型Fig.4 Marmousi's attenuation and velocity model(a)衰减模型;(b)速度模型

图5 PML边界和CFS-NPML边界下的Marmousi地震记录Fig.5 Marmousi seismic records under PML boundary and CFS-NPML boundary(a)PML边界;(b)CFS-NPML边界

根据图5可以看出，在粘滞性介质中地震波场能量由浅到深，逐渐变弱，深层反射振幅减弱,分辨率逐渐降低。在深度约3 km分界线以下PML吸收边界条件下的地震记录消失，而CFS-NPML吸收边界条件下的地震记录仍能分辨。但当到达4 km深度时，传统PML边界条件下的数值模拟出现不稳定现象，而在CFS-NPML边界条件下的地震记录未出现任何明显变化，由此可看出CFS-NPML吸收边界能够有效地压制虚假反射，阻断了反射波淹没地震记录提高了信噪比。图6为在不同边界条件下放大的振幅和能量变化图，可以明显看出，使用CFS-NPML边界条件进行正演模拟的振幅大小略强于PML边界正演和能量变化相比与PML边界条件稳定，从而证明CFS-NPML边界稳定性和吸收效果上强于PML边界条件。

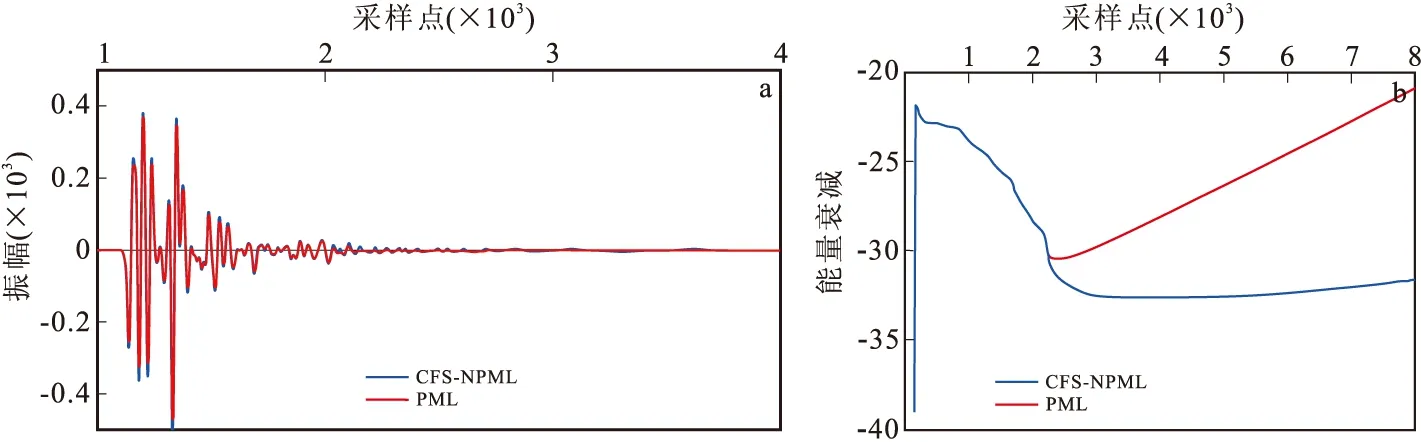
图6 不同边界振幅变化放大图和能量衰减变化放大图Fig.6 Amplification diagram of amplitude changes at different boundaries variation diagram of energy attenuation(a)振幅变化放大图;(b)能量衰减变化放大图

为进一步说明CFS-NPML吸收边界的吸收效果及稳定性、可行性，给出了PML和CFS-PML边界条件下的不同时刻波场快照。对比图7(a)和图7(b)可以看出当t=800 ms时，实现的两种吸收边界均能很好地反应声波在粘滞性介质中的传播规律，并且在边界处，没有看到明显的虚假反射现象，可以验证两种吸收边界均能够有效吸收到达边界的声波。通过图8可以看出，当t=2 800 ms时，PML与CFS-NPML边界吸收条件在边界条件内发生微妙变化，PML边界处的波场开始模糊看不清，而CFS-NPML边界处的能够保持其稳定的波场记录。根据图9可以明显看出，当t=4 800 ms时，CFS-NPML边界条件内的波场值频率大于PML边界内的频率，且保持其粘性衰减特性，这与前面主要对波的低频成分进行吸收一致。

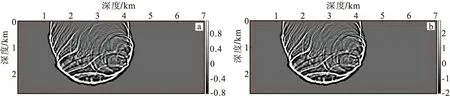
图7 t=800 ms处 PML边界和CFS-NPML边界的波场快照Fig.7 t=800 ms snapshot of the wave field of the T-PML boundary and the CFS-NPML boundary(a)PML边界;(b)CFS-NPML边界

图8 t=2 800 ms处 PML边界和CFS-NPML边界的波场快照Fig.8 t=2 800 ms snapshot of the wave field of the T-PML boundary and the CFS-NPML boundary(a)PML边界;(b)CFS-NPML边界

图9 t=4 800 ms处 PML边界和CFS-NPML边界的波场快照Fig.9 t=4 800 ms snapshot of the wave field of the T-PML boundary and the CFS-NPML boundary(a)PML边界;(b)CFS-NPML边界

复频移PML虽然在计算时加入了更多的辅助变量，但是与经典PML的分裂式相比，采用了非分裂形式，在求解运算时减少了大量的卷积运算。从表1也可以看出，PML在黏声正演模拟中所需时间比CFS-NPML所需时间多，所占内存多，可以看出在同样条件下CFS-NPML在计算效率和存储空间上的优势。

表1 不同边界条件黏声正演模拟计算时间和存储量

3 结论

笔者通过对四种吸收边界条件对虚假反射的吸收效果进行对比，然后更进一步地进行对基于Marmousi模型的CFS-NPML分数阶粘声正演模拟研究，将PML、CFS-NPML边界条件应用到接近实际地层条件的分数阶粘声正演模拟中，并采用Marmousi模型来测试边界条件在复杂地层下的稳定性、可行性。通过对PML、CFS-NPML两种边界条件在数值模拟中的效果对比可得到如下结论：

与C-E吸收边界、廖氏吸收边界相比PML和CFS-NPML边界条件能够明显地压制波场的虚假反射，并保持其稳定性；与传统PML边界条件相比，CFS-NPML边界能够在分数阶粘声正演模拟中保持其鲁棒性、可行性，并且能够有效吸收高角度入射波/掠射波以及瞬逝波，避免发生虚假反射现象而淹没地震记录，提高了数值模拟信噪比；在CFS-NPML边界条件内的分数阶粘声正演模拟能够很好地反映声波因地下介质的粘滞性，而产生对波的吸收和衰减等特性。有助于我们更好地认识地震波在粘性介质中的传播规律，对补偿因地下介质粘滞性因素影响而损失的地震波能量具有深远意义。