基于VMD与改进小波阈值的地震信号去噪方法研究

乔 云， 李 琼，1b， 钱浩东， 宋 鑫

(1.成都理工大学 a.地球物理学院,b.地球勘探与信息技术教育部重点实验室，成都 610059；2.中国石油集团 川庆钻探工程有限公司钻采工程技术研究院，广汉 618300)

0 引言

去噪是地震信号处理的重要一环，而小波变换是地震信号去噪的常用手段。Donoho DL等[1]提出了一种基于小波变换的去噪方法，即小波阈值去噪法。小波阈值函数分为硬阈值函数和软阈值函数，通常认为小于阈值的小波系数是由噪声产生的，而大于阈值的小波系数才是由有效信号产生[2]。因此硬阈值函数将小于阈值的小波系数置零，这便会导致硬阈值函数在阈值点处跳动；软阈值函数则是把小于阈值的小波系数置零的同时，将大于和等于阈值的部分减去阈值，这样虽然保证了阈值函数的连续性，但是在小波系数大于阈值的部分有效信号的能量也会有所损失[3]。在进行小波阈值去噪后，硬阈值函数处理后的信号相较于软阈值处理的信号会更为粗糙[4]。两种阈值函数都有各自的优缺点，笔者在前人研究的基础上，提出一种改进的阈值函数，能够通过两个参数灵活调节阈值函数，既可以保证函数在阈值点处的连续性，也可以解决小波系数的偏差问题。

Konstantin等[5]提出的变分模态分解(Variational Mode Decomposition，VMD)是一种自适应分解方法，将信号分解为有限个模态分量，并确定各模态分量的中心频率和带宽，因此可以很好地应用与地震信号的分解。

由于改进小波阈值去噪的方法与变分模态分解方法都有各自优点，又能很好地处理非平稳信号，因此笔者将两种方法相结合，提出一种新的地震信号去噪方法。首先将地震进行变分模态分解，得到有限个模态分量，将这些模态分量进行改进小波阈值去噪处理，然后将去噪后的模态分量进行重构，得到去噪后的信号，将两种方法结合，能尽可能地保留地震信号中的有效信号，并压制随机噪声。

1 方法原理

1.1 小波阈值去噪原理[6-7]

1)确定合适的小波基函数并确定其分解层数，分解得到不同层数下的小波系数，笔者选择db3，分解层数为2层。

3)选取适当的阈值函数，对每层分解层的小波系数进行改进小波阈值去噪。

4)对处理后的N层系数进行小波重构得到去噪后的信号。

小波阈值去噪流程图如图1所示。

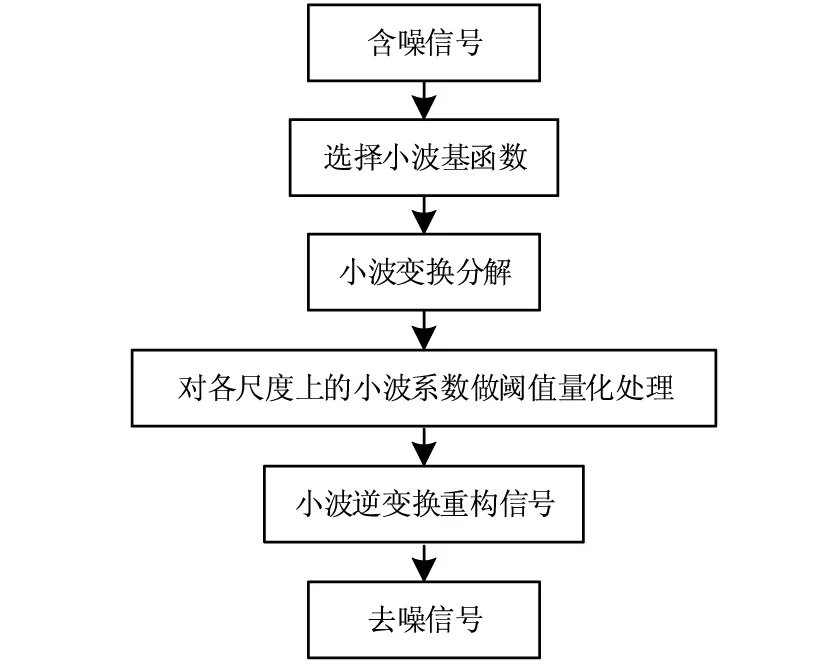
图1 小波阈值去噪流程图Fig.1 Wavelet threshold denoising flowchart

1.2 改进的小波阈值函数

传统的阈值函数分为软阈值和硬阈值函数。

软阈值函数[8]为式(1)。

(1)

硬阈值函数[9]为式(2)。

(2)

式(1)和式(2)中：wj,k为小波分解系数，Wj,k为阈值处理后的小波系数。小波软阈值函数和硬阈值函数在去噪中已经有很多应用，然而硬阈值函数在阈值点处不连续以及软阈值函数的恒定误差问题仍然会对去噪效果产生一些影响。因此笔者在前人的研究的基础上，设计了一种新的阈值函数，综合了软阈值与硬阈值函数的特点(式(3))。函数图像如图3所示。

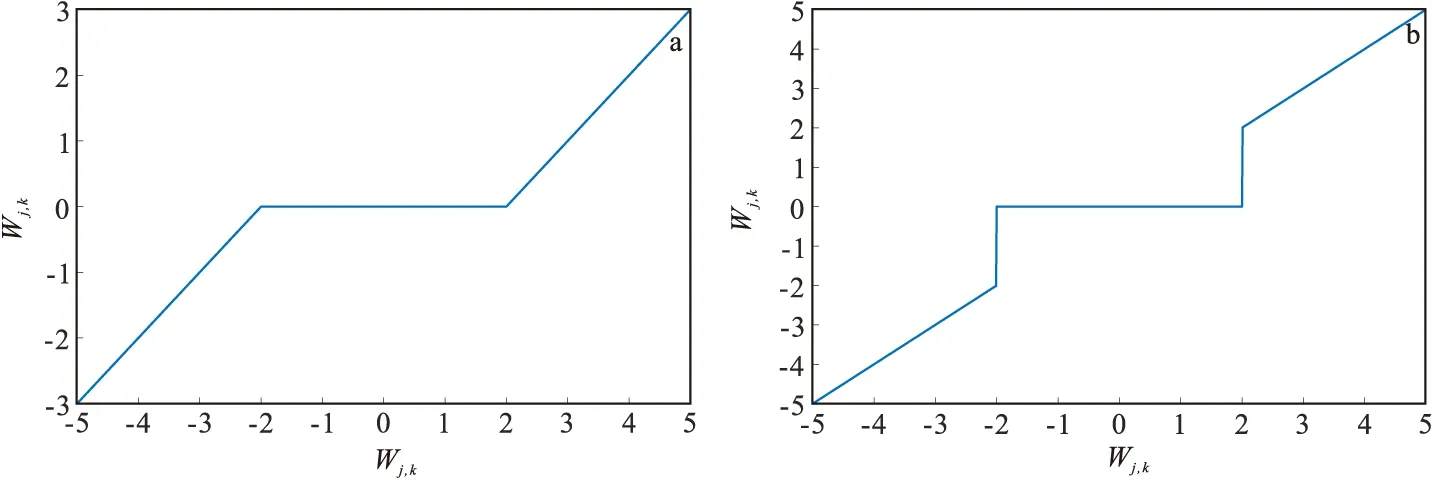
图2 阈值函数对比Fig.2 Threshold function comparison(a)软阈值函数;(b)硬阈值函数

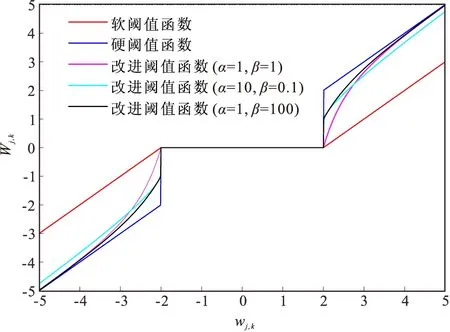
图3 改进阈值函数Fig.3 Improved threshold function

(3)

式(3)和图(3)中:wj,k为小波分解系数；Wj,k为阈值处理后的小波系数。

该函数有如下特点：

1)在阈值点处，函数是连续的，因此能克服硬阈值函数在阈值处不连续的缺点。

2)满足是一个奇函数的条件，使处理信号时对正负信号能够达到相同的效果。

3)含有两个可以调节阈值函数的参数(α和β)，可通过更改两个参数让函数在大于阈值后渐近线迅速靠近硬阈值函数，能够保留有效信号的能量克服了软阈值函数中的恒定误差问题。

在实际去噪过程中，需要根据噪声大小和实际情况来调节两个参数，通过调节参数试验，以便能获得更好的去噪效果。

1.3 变分模态分解

VMD是一种自适应且高效的信号分解方法，可将非平稳信号按中心频率和带宽的不同分解成为不同的模态分量，由此将有效信号和噪音在按不同的模态分量来分开。VMD的分解过程实际是变分问题的构造和求解过程。其约束变分模型为式(4)。

(4)

2 实验仿真及效果评价

为评价该去噪方法的有效性，将该去噪效果与其他传统单一去噪效果进行对比。首先生成一条单道合成地震记录，在该信号中加入不同分贝的高斯白噪声，再分别用VMD去噪、硬阈值小波去噪、软阈值小波去噪、以及这里提出的联合改进方法去噪，并计算信噪比(SNR)对比去噪效果。笔者改进小波阈值参数为α=1,β=1、选用db3小波进行分解，分解层数为2层。

信噪比的计算公式见式(5)。

SNR=10lg∑f2(n)/(∑(s(n)-f(n))2

(5)

式中：f(n)为原始信号;s(n)为去噪后的信号。

图4为一条合成的单道地震记录，图5是添加高斯白噪声后的信号，其信噪比为SNR=5.309 3 dB，图6为含噪信号的VMD分解，图7、图8、图9为分别为VMD的去噪结果、小波硬阈值去噪结果、小波软阈值去噪结果，信噪比得到了一定的提高，但是可以看出小波硬阈值去噪和软阈值去噪后波形幅度也有所衰减，丢失了部分有效信号。而图10为笔者提出的改进方法的去噪结果，从图10中可以看到，噪声很大程度上得到了去除，并且也克服了小波硬阈值去噪和软阈值去噪时的振幅损失问题，通过计算信噪比，笔者提出的改进去噪方法去噪后得到的信噪比明显高于其他三种方法。

图4 原始信号Fig.4 Original signal

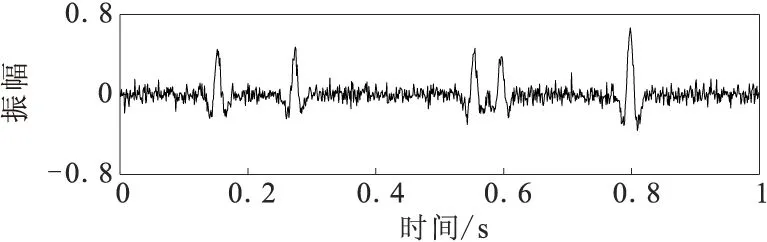
图5 含噪信号(SNR=5.309 3 dB)Fig.5 Noisy signal

图6 VMD分解Fig.6 VMD decomposition(a)含噪信号;(b)至(f) IMF分量

图7 VMD去噪结果(去除IMF1-IMF3)(SNR=9.513 6)Fig.7 VMD denoising results

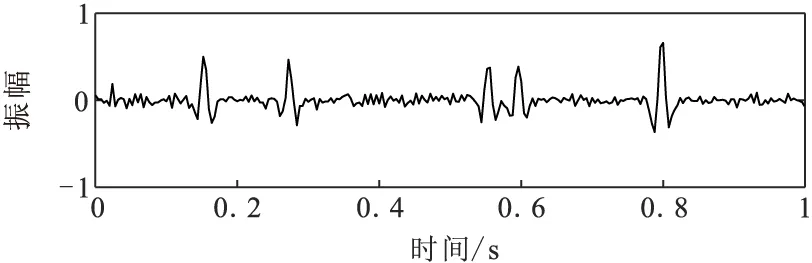
图8 小波硬阈值去噪结果(SNR=9.027 6 dB)Fig.8 Wavelet hard threshold denoising results

图9 小波软阈值去噪结果(SNR=8.404 4 dB)Fig.9 Wavelet soft threshold denoising results

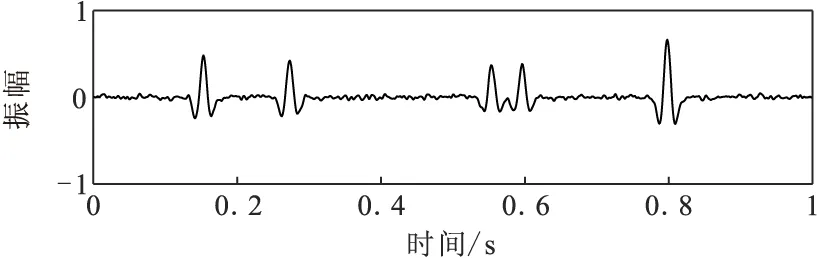
图10 改进方法去噪结果(SNR=10. 594 7 dB)Fig.10 Denoising results of improved method

为了评价本文改进去噪方法在不同信噪比下的去噪效果，又进行了以下实验。在信号中加入四种不同能量大小的白噪声(20 dBb、22 dBb、24 dBb、26 dBb)，分别用VMD分解重构去噪、小波硬阈值法去噪、小波软阈值法去噪和本文改进方法去噪，再分别计算不同噪声强度下去噪后的信噪比，去噪前后的信噪比如表1所示，由表1可以看出，经过本文改进方法去噪后信噪比提升最大，其次是VMD分解重构去噪、小波硬阈值法去噪、小波软阈值法去噪。经过不同噪声能量下各种方法去噪效果的对比，证实了本文提出的改进去噪方法去噪的有效性。

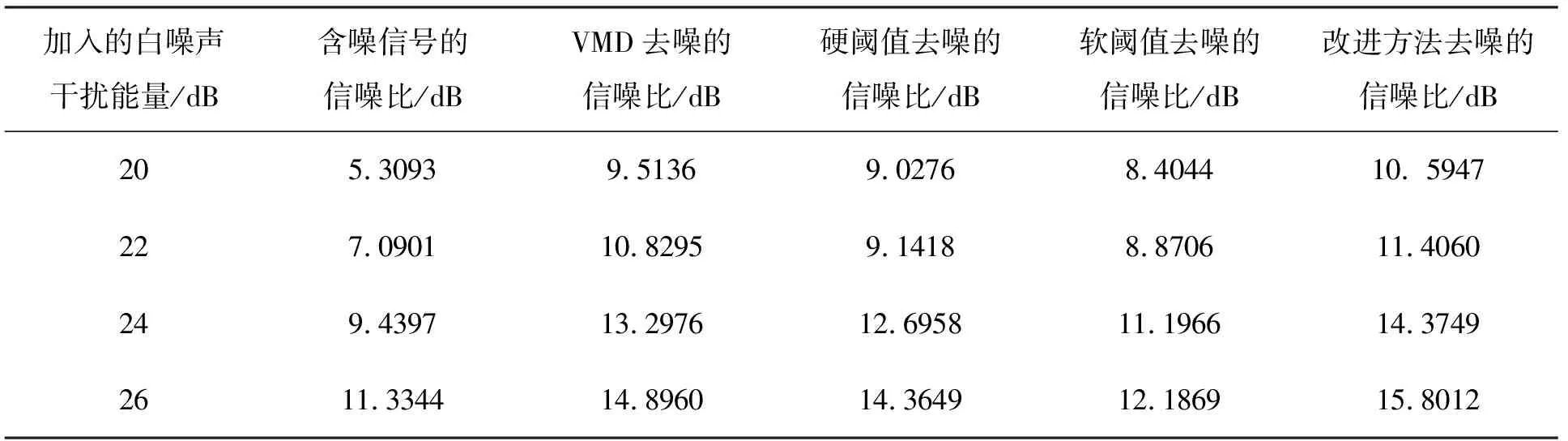
表1 加入不同分贝高斯白噪声的去噪效果

3 实际地震资料的处理

图11是某工区一个含有大量噪声的实际地震剖面。由图11可以看到，除能量很强的同相轴够能勉强分辨外，其余能量较弱的小振幅被噪声淹没，反射波同相轴不清晰，无法有效识别。图12(a)、图12(b)、图12(c)、图12(d)是分别用小波硬阈值、小波软阈值、VMD和本文提出的改进方法对该含噪实际地震剖面处理后的结果，由图12可以看出，经过四种方法去噪后，大部分随机噪声都得到了有效去除，反射波同相轴明显变得更为清晰，但是对于细节部分，如图12中圈出的反射波同相轴，这里提出的改进方法去噪后其同相轴的连续性明显优于其他三种方法，并且对于在剖面上能量较弱的有效信息也能够更有效地保留，信噪比大大提高。图13(a)、图13(b)、图13(c)、图13(d)是分别用小波硬阈值、小波软阈值、VMD和本文提出的改进方法对该含噪实际地震剖面处理后的得到的噪声分量，由图13可以看出，四种方法都去除了大量噪声，在噪声残差剖面中，也没有明显看出反射波同相轴的特征，说明了在去噪过程中没有明显损失有效地震信息，地震信号得到有效保留。

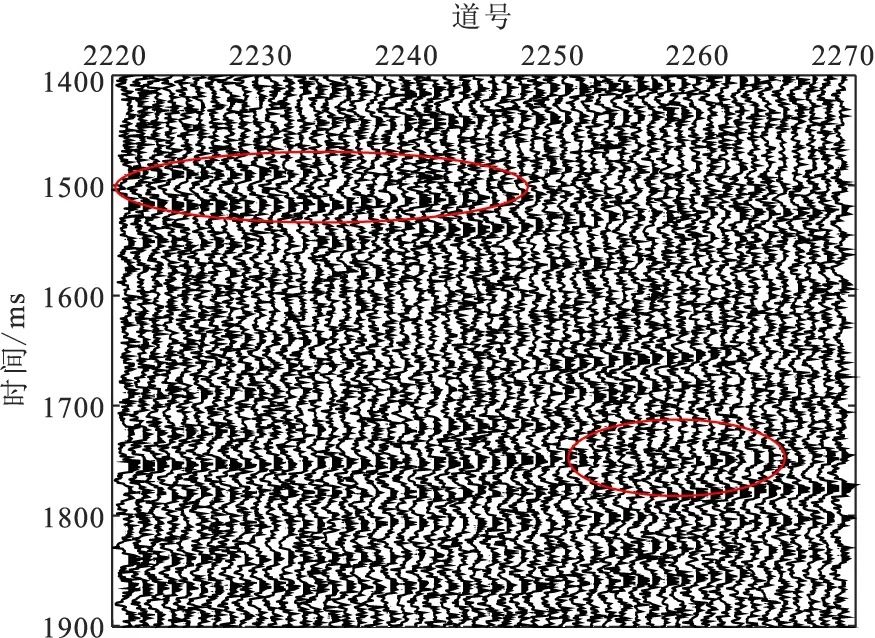
图11 含噪声的实际地震剖面Fig.11 Real seismic-section with noise

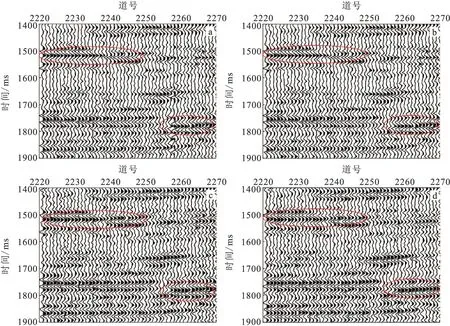
图12 含噪实际地震剖面的去噪对比Fig.12 Denoising comparison of real seismic-section with noise(a)小波硬阈值法去噪结果；(b) 小波软阈值法去噪结果；(c)VMD去噪结果；(d)本文改进方法的去噪结果

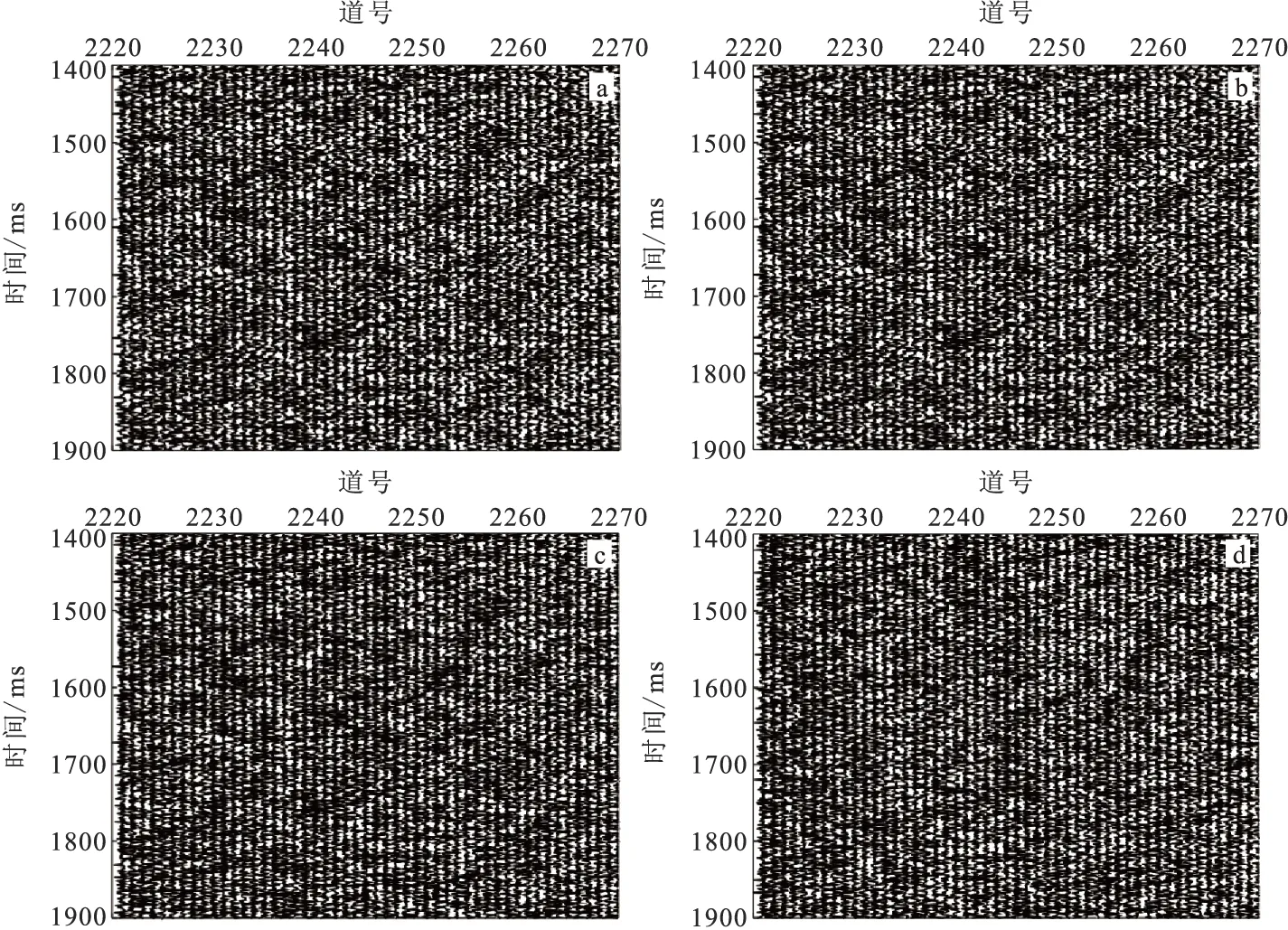
图13 噪声分量Fig.13 Noise component(a)小波硬阈值法去除噪声分量；(b) 小波软阈值法去除噪声分量；(c)VMD去除噪声分量；(d)本文改进方法去除噪声分量

4 结语

通过改进小波阈值函数，结合了传统软阈值函数和硬阈值函数的优点，克服了两种函数的缺点，提出一种新的可通过改变参数来调节阈值的函数，以便在进行去噪的同时尽可能保留有效信号。同时将VMD分解与改进小波阈值去噪法相结合，利用VMD的多尺度自适应分解特点，进一步提高了去噪效果，通过对单道合成地震记录的仿真去噪实验，计算去噪后的信噪比，以及对含噪实际地震剖面的去噪处理，都证明了本文提出的改进方法能够有效对地震信号进行去噪，提高信噪比，且去噪效果优于其他三种单一的去噪方法，在去噪时能够保留更细节的有效信息。