高密度电法中的电极位置校正方法研究

聂小力， 毛 聪， 王世界， 欧泽文， 罗敏玄

(中国地质调查局 长沙自然资源综合调查中心，宁乡 410600)

0 引言

高密度电阻率法,由于其高效性和便利性在工程勘探领域内广泛应用。在野外测量时，只需将全部电极(几十至上百根)置于设计剖面的各测点上,采集系统便可利用程控电极转换装置实现数据的快速和自动采集。采集过程中，主机记录每组电极组合方式下的电位值和发射电流值，并根据设置的单位电极距计算对应的装置系数K，进而求得视电阻率值。但是实际施工中，电极的实际布置点位受场地限制常常需要偏移，这在南方水田种植区内工作时尤为常见。当电极偏移布置时，电极距及A、B、M、N电极间的相对位置已不满足设计情况，采集系统根据单位电极距计算得到的对应装置系数也不符合实际情况，这势必对测量结果造成严重影响。为得到剖面位置校正方法，根据点电流源电场分布规律[1]，可得到不同电极组合情况下的视电阻率表达式，并利用解析法对均匀半空间中无电极偏移和有电极偏移两种情况下的视电阻率响应进行数值模拟，证明了剖面校正的必要性，再从装置系数K入手给出了电极位置校正的方法。最后选取地势平坦，地质条件单一的地电断面，分别按有(无)偏移距布置电极，并对有电极偏移的剖面数据用本文方法做校正后，对比实测的无电极偏移数据，验证了校正方法的有效性。

1 视电阻率计算公式

ΔUMN=UM-UN=

(1)

根据式(1)移项后可以得到用点电极测量时的大地视电阻率表达式为式(3)。

ρ=2π/(1/AM-1/BM-1/AN+1/BN)·

(ΔUMN)/I=K(ΔUMN)/I

(2)

式中

K=2π/(1/AM-1/BM-1/AN+1/BN)

(3)

当测量装置为温纳装置(AM=MN=MB=a)时，对应的装置系数化为Kwenner=2πa。若受施工环境限制，供电电极和测量电极无法布置在设计点位上，实际位于A′、B′、M′、N′，此时装置系数K不再能简化，而采集系统仍然按照设计的单位电极距逐个测量点计算装置系数，所测视电阻率将受影响而变为：

ρ′=S×ρ

其中

S=a(1/A′M′-1/B′M′-1/A′N′+1/B′N′)

(4)

这与准确的视电阻率相差一个由电极位置而决定的电极位置影响因子S，必然对测量结果带来不良影响。为消除这一不良影响，需逐个测点计算其电极位置影响因子S，再用测得的视电阻率值除以这一因子，即可得到不受位置影响的视电阻率。

2 解析法数值模拟

为研究电极位置影响情况，验证校正方法的科学性，设计均匀半空间地质模型，利用MATLAB软件[3-4]采用解析法,对高密度电法温纳装置下的视电阻率响应进行数值模拟[5-6]。在模拟过程中，均匀半空间电阻率值为100 Ω·m，共设电极位50个，点距为10 m，供电电流为1 A。分别模拟计算无偏移距和有偏移距情况下的视电阻率响应，具体点位布置情况如图1所示。

图1 数值模拟点位设计图Fig.1 Stations of the numerical simulation

表1给出了均匀半空间模型中各测点的点位坐标，以及第一层的数值模拟电阻率响应和对应测点下的电极位置影响因子。图2为数值模拟电阻率响应图。

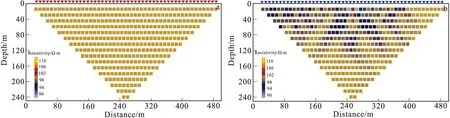
图2 均匀半空间数值模拟Fig.2 Numerical simulation of uniform half space(a)无偏移距视电阻率响应;(b)有偏移距视电阻率响应

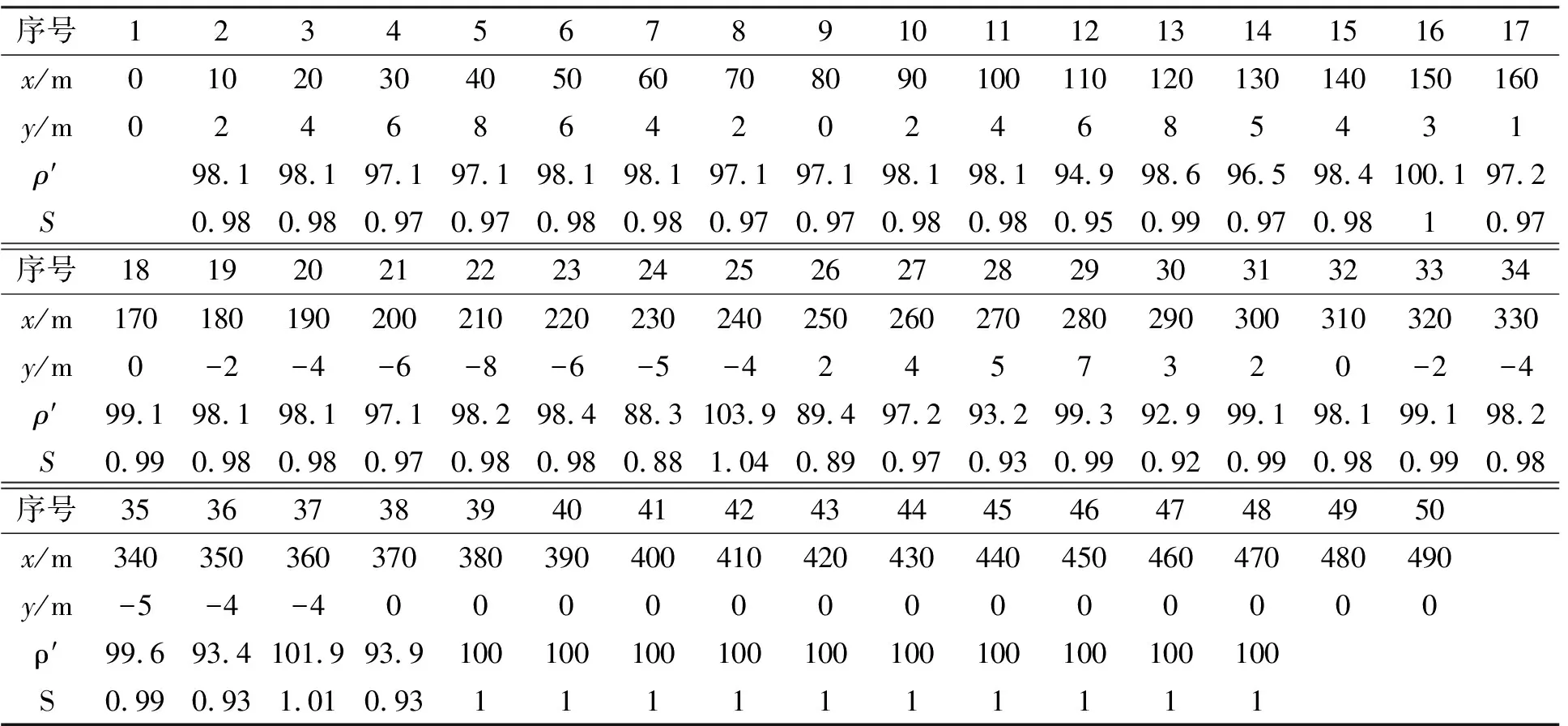
表1 数值模拟点位坐标及电极位置影响因子表

x沿剖面的距离 y垂直剖面方的偏移量 ρ′偏移情况下的电阻率响应 S:电极位置影响因子 表中只列均匀半空间第一层的数据

对比表1中偏移量与电阻率响应的关系可知，当电极位置不准确时会对测量结果造成影响，当偏移距离达到电极距的50%时，测量结果误差比约为5%(测点12)，当偏移距离达到电极距的100%时，误差比约为10%(测点26)。分析电阻率响应图可以看出，当无偏移距时，图2(a)模拟计算得到的视电阻率响应表现为均匀的半空间，这与实际模型相符。图2(b)为有偏移距时模拟计算得到的视电阻率响应，可以看出当电极位置不准时，点位变形越严重的区域视电阻率响应畸变也越严重。偏移距越大，误差比越大。这将给后期的反演和解释工作引入假异常。因此，研究找出能消除这一不良影响的方法很有必要。

3 校正方法应用效果

得到校正方法后，通过对实测数据进行电极位置校正，并对比无偏移距时的测量结果[5]，以此来说明校正方法的有效性和可行性。

实测剖面位于第四系覆盖区，结合地质资料及钻探资料可知剖面范围内地质环境稳定，地势平坦，可近似认为在我们人为给出电极偏移尺度下，由于断面电性差异带来的视电阻率变化可忽略不计。设计无偏移距和有偏移距两种情况下的剖面实施数据采集，共有点位56个，点距10 m，工作时采用重庆地质仪器厂生产的DUK-4型高密度电法仪，供电高压为500 V，供电时长为0.5 s，停供时长为0.2 s。点位布置情况如图3所示。

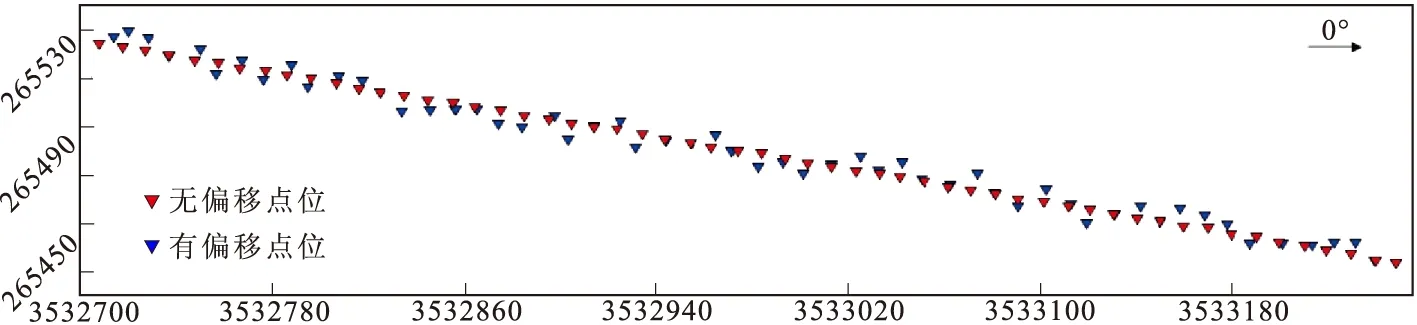
图3 实测剖面点位布置图Fig.3 The layout of the measured section points

对比图4(a)和图4(b)可以看出，电极偏移使得视电阻率分布特征发生了畸变。校正后视电阻率特征如图4(c)，校正效果显著。利用视电阻率数据反演所得结果如图5所示。可以看出在地下30 m以浅范围内，反演结果畸变严重。其中在小号点附近，0 m～180 m范围内的低阻异常体在规模和形态上变化严重，已无法识别，在地表20 m范围内的局部异常体在形态和展布位置上也受到了不同程度影响。

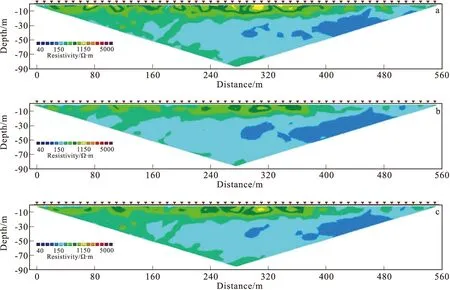
图4 实测视电阻率拟断面图Fig.4 Map of resistivity profile(a)无偏移实测电阻率拟断面图;(b)有偏移实测电阻率拟断面图;(c)有偏移校正后的实测电阻率拟断面图

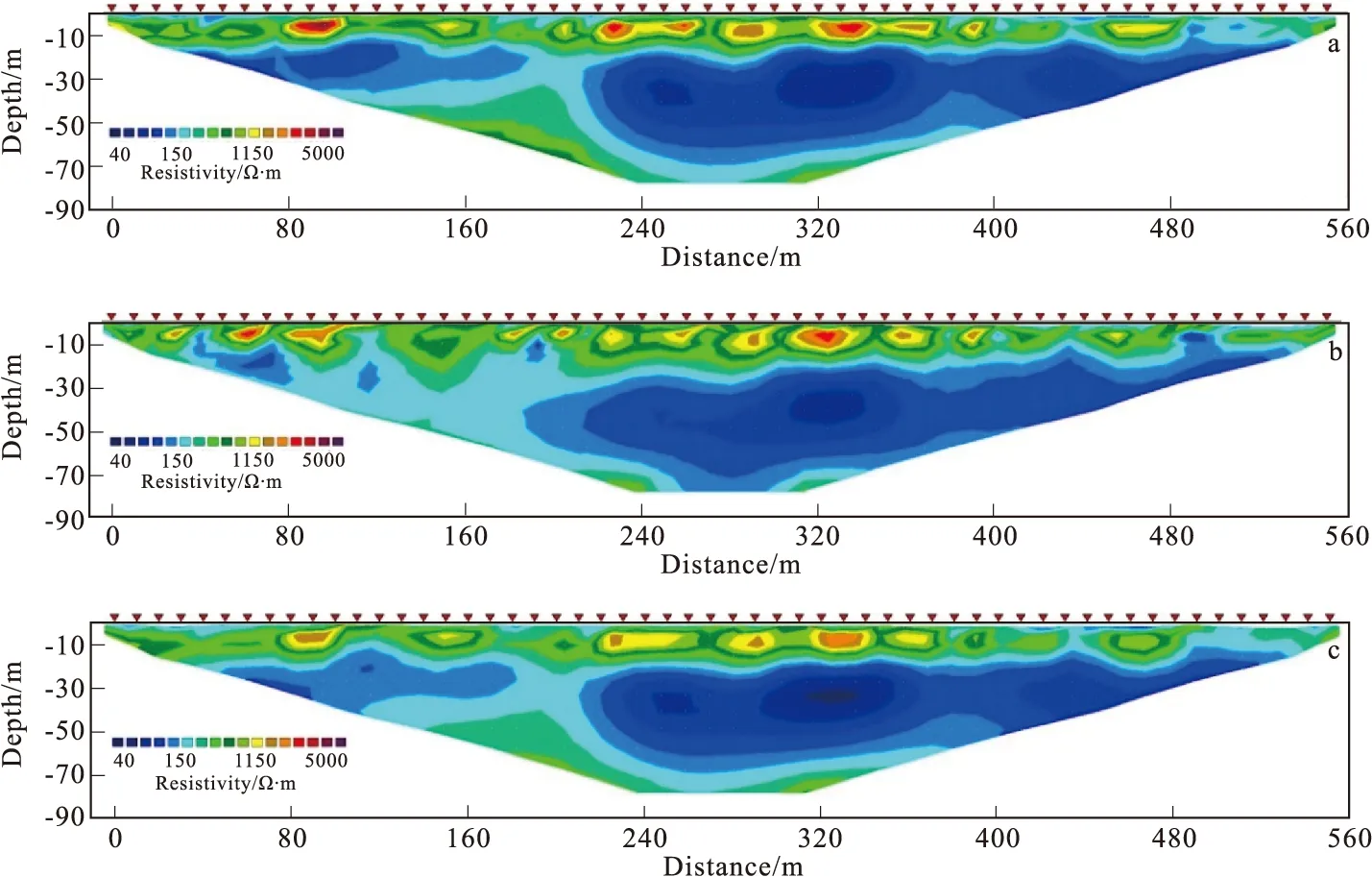
图5 反演电阻率断面图Fig.5 Map of inversion resistivity(a)无偏移实测电阻率拟断面图;(b)有偏移实测电阻率拟断面图;(c)有偏移校正后的实测电阻率拟断面图

通过对有偏移距情况下的实测数据进行电极位置校正后，再反演得到电阻率断面图如图5(c)所示，对比图5(c)和图5(a)可以看出，0 m～180 m范围内的低阻异常体形态已得到很好地校正，地表20 m范围内的局部异常体，特别是在空间位置上也得到了明显地校正。

以无偏移情况下的实测电阻率作为标准电阻率，分别计算有电极偏移ρoffset和其校正后的数据ρcorrect与标准电阻率的误差比[7-8]，计算公式为式(5)。

(5)

结果如图6所示。

图6 误差比断面图Fig.6 Error ratio profile(a)无偏移-有偏移误差比;(a)无偏移-有偏移校正误差比

4 结论

笔者从点电流源的电场分布入手，推导得到了电极位置校正的方法和具体计算公式，通过对均匀半空间模型进行数值模拟，直观表达了电极位置的不准确对电阻率断面带来的影响，这一影响主要表现为电极偏移越严重的地方视电阻率测量值畸变也越严重，浅部数据受影响程度要大于深部数据，这是由于当电极距达到某一程度时，电极偏移的尺度对其而言可忽略不计。通过对实测数据进行处理，证明了所推导的电极位置校正方法的有效性和可行性，也证明了当有电极偏移存在时，对实测数据做剖面位置校正能够有效地剔除假异常，还原真实的电阻率分布。