一种基于Dynamo的复杂地质体参数化三维建模方法
马钰栋, 唐君辉
(上海申元岩土工程有限公司, 上海 200011)
在勘察过程中推广基于BIM技术的应用是工程地质和地质信息科学领域的一个热门问题[1]。随着大数据技术、计算机图形学理论、3S技术等技术的出现和发展,创建复杂结构的三维地质体模型的思路和方法也得到了极大拓展[2]。
参数化建模多用于具有形态已知的结构体的模型创建。然而利用勘察数据建立地质体模型有其特殊性。首先地质界面的构造复杂,存在尖灭、断层等地质现象;其次,真实地质构造是未知的,地层曲面的具体形态往往无规律可言;再者,勘察过程中只能获取场地内勘探点的数据,根据地质资料分析和预测整个场地的地质形态;最后,通过勘察成果建立地质体模型时,需保证其合理性,如保证层面之间无互相穿插的现象[3]。朱凤贤等[4]在建模过程中,分别对不同的情况进行处理,在地层连接分类中,总结出6例地层反演缺失的情况。杜子纯等[5]讨论了地层缺失、倒转、重复等特殊地层情况并进行实例论证,提出了一种基于地层沉积顺序的统一地层序列方法。何紫兰等[6]基于GOCAD软件对复杂地质体的三维实体建模方法,讨论了针对4种复杂地质体进行建模的具体实现方法,详细论证了逆褶皱地质体和非层状地质体。但上述3种划分地质界面层序的方法,均是基于穷举法的思想,不能便捷地对于所有勘探孔揭露的土层做服务于地质建模的地层划分。本文提出一种利用母版层序、多所有钻孔进行地质界面分层的方法。
对复杂地层建立三维地质体模型的方法较多。李昌领[7]采用以面元模型和体元模模型基本单元进行建模的方法,在建模过程对复杂地层体能进行较好的处理,但不能充分展示地质实体形态。郭艳军等[8]提出了一种利用钻孔数据作为数据源,考虑交叉折剖面约束的三维地质体建模方法,该方法可以模拟钻孔间复杂的地质现象,但该方法建立的模型光滑度不高。邓小龙等[9]利用三维激光扫描技术获取精细集合数据,基于Geomagic Studio利用点云数据建立了复杂地质体的CAD曲面模型,但三维激光扫描技术一般只能获取地质体形状表面的点云数据。He等[10]和Høyer等[11]基于多层DEM建立了三维地质体模型,建模流程简单,易于可视化展示,但该方法难以处理非连续地质体。郭甲腾等[12]用地表边界模型和广义三菱柱实现了对地质体的地上和地下部分进行三维集成建模。陈国旭等[13]以勘察剖面作为数据集,建立了三维地质体模型。以上叙述的创建三维地质体的方法都属于显式建模方法,通常以此类方法建立的模型与真实地层有一定差别。
隐式建模是基于采样数据,利用空间插值方法拟合空间曲面函数,生成三维可视化模型的一种建模方法[14]。但由于信息量庞大和地质体结构的复杂性问题,一般隐式建模方法所建模型良莠不齐,对数据的利用效率较低,为了建立模型,需要牺牲一定的精度,如忽略尖灭和透镜体等[15]复杂地质结构或者对勘探点间的数据没有合理的预测;而精细化建模需要工程人员结合地质剖面或者其他经验来投入一定的时间对模型进行细部调整[16-19]。此外,一般地质类的建模软件如gocad,虽然其功能强大,但其所建模型和其他工程类建模软件并不能很好对接[20]。因此如何利用勘察数据,快速建立起精度高的、符合真实地层分布参数化三维地质体模型是BIM在岩土工程勘察利用中的一个重点。本文以勘察勘探点数据为数据源,从数据处理、参数化地层曲面的形成与切割、形成地质体模型等方面,提出一种基于Dynamo插件,通过勘探点数据源拟合空间曲面函数,进而生成参数化三维地质体模型的隐式建模方法。这种方法建模灵活,自动化程度高,提高了勘探点间地层信息的准确性,并结合实际工程表明其可行性及高效性。
1 关键步骤
三维地质体模型反映了地层分布的形态和底层之间的宏观拓扑关系。它的准确性取决于客观地表达地质体的空间分布和拓扑关系。使用勘察成果建立三维地质体模型时,勘探孔平面坐标、孔口高程、勘探点内各地层分界面高程(深度)数据控制着模型的构建形态。因此,由勘探点形成的点云的空间位置和地层面的模拟是对复杂地质体进行建模的关键。
根据勘察成果以点-面-体的形式建立三维地质体模型的关键步骤如下:
1)对勘察成果中的勘探孔数据进行整理,提取勘探孔的平面坐标、孔口高程、各地层界面高程。然后建立一个适用于所有勘探孔的母版层序,保证每个勘探点分层数和层序相同,然后提取每层土的物理力学性质数据,并保证这些土层属性参数与母版层序的土层一一对应。
2)对勘探孔数据进行普通Kriging插值,然后根据插值点数据判断拟生成的地层曲面是否会相互穿插,若有穿插,则进行数据矫正。
3)将处理好的数据导入Dynamo插件,利用勘探点数据和插值数据通过自编节点程序生成点云,再由点云生成NURBS(Non-Uniform Rational B-Splines)地层曲面。
4)通过自编节点程序,用凸包算法在勘探孔中搜索出凸包点,由凸包点生成凸包络线,再由凸包络线生成切割曲面,用切割曲面实现对NURBS地层曲面的切割。
5)剔除勘探孔控制范围外的地层曲面,经过自编节点程序运算,由地层曲面生成地层实体。
6)将勘探点实体和地层实体导入Revit中,生成土层模型实例,再通过自编节点程序,将土层的物理力学性质数据导入模型,即形成三维地质体模型。
基于Dynamo的复杂地质体参数化三维建模流程如图1所示。
2 建模方法主要过程
2.1 母版土层层序的建立
在现实地层中,单个勘探孔揭露的地层常常会出现地层缺失、倒转、重复等情况,这给地层曲面的建模造成很大影响,导致出现不同地层曲面的错误连线或生成的地形曲面出现互相穿插。因此单个工程的地质界面分层需适用于整个场地的勘探点,以保证勘探孔之间不会错连。
建立母版土层层序的步骤如下:
1)建立基本编号规则。首先将土层序号以数值表达,以上海土层为例,将土层名字主要土层记为同样的数字,其中的亚层则在小数点后进行增加数值,如②1的数值表达记为2.1,③t的数值表达记为3.5,⑤1-2的数值表达记为5.12。那么单个勘探孔所揭露土层(①,②1,②3,③,③t,③,④,⑤1-1,⑤1-2,⑤3,⑥)则可记为列表(1,2.1,2.3,3,3.5,3,4,5.11,5.12,5.3,6),如图2所示。列表按照土层沉积顺序进行排序,沉积年代越晚的土层的序号越小,土体从上至下的土层在列表中的序号从0开始依次增加,最深的土层在列表序号为n-1,n为该列表的长度。
2)勘探孔分类。遍历所有勘探孔,若勘探孔r揭露的土层分层数值列表R中,且列表中存在重复值,则勘探孔r揭露的土层即为重复型土层。若勘探孔r的土层分层数值列表R中,存在第i项同时小于第i-1项和第i+1项且列表中无重复值,则勘探孔r揭露的土层即为倒转型土层。搜索所有揭露了异常土层的勘探孔,根据不同的重复地层、不同的倒转地层情况,将其分类,其集合记为Y。

图1 基于Dynamo的复杂地质体参数化三维建模流程

图2 将土层程序转化为数值列表
3)建立第一版母版土层层序(图3)。先遍历所有勘探孔,根据其揭露的土层对勘探孔进行分为p类,揭露的土层包含同一种层序的勘探孔数量为z个,其集合为[z1,z2,…,zp],则其中最大的值为zq=max[z1,z2,…,zp],令第q类的勘探孔所揭露的土层为第一版母版土层分层,记为S1。此时的母版土层为场地典型土层。

图3 土层层序分类
4)迭代法建立包含所有土层的母版土层层序。再次遍历所有勘探孔,每个勘探孔揭露的土层分层数值列表记为Rr。将第一版母版分层中S1的元素与Rr中的元素进行比较,若Rr中存在S1中不存在的元素,则将其按原顺序加入母版土层。当母版土层在该过程中迭代完毕,生成第二版母版土层,记为S2。此时母版土层中已包含该工程勘探孔所揭露的内所有土层。
5)根据异常土层调整第二版母版土层层序。遍历Y中的异常勘探孔,其土层数值列表为R,异常土层在列表中的序号为i,将列表中的第i-1、i、i+1项切片,然后查找S2列表中是否有切片列表相同的数值排列,若有,则保持S2不变;若没有,则根据切片数值修改S2列表的数值排列,生成最终版母版土层层序,记为S。
6)根据母版土层层序,统一所有的勘探孔土层层序。母版土层层序包含所有的土层及排列顺序,其他勘探孔的土层层序按照模板的土层层序进行修改,在缺失层添加一个厚度为0的层。修改勘探孔土层层序过程如图4所示。
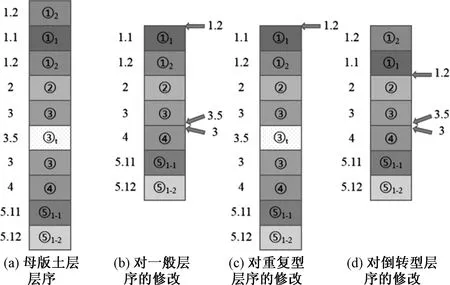
图4 应用母版土层层序统一土层地质界面分层
应用母版土层层序统一所有勘探孔揭露所土层地质界面分层,使得勘探孔中每一地质层面一一对应,避免在建模过程中地质界面错连和插值过程数据不匹配。
2.2 Kriging插值
对于岩土体界面的数字化表达是基于 BIM 的创建三维地质体模型的基础[18]。在实际勘察工作中得到的原始数据大多是离散的,散乱地分布在研究区域内。所以在建立三维地质体模型的过程中需要对空间数据进行插值,所选择的插值方法的精确度对于地层模拟的结构合理性和数学表达的准确性极为关键。
考虑原始数据的样本数量和拟合效果时,本文采用Kriging法进行建模插值。在具体应用时,通过引进以勘探点之间的水平距离为自变量的变异函数来计算权重因子,该变异函数能体现变量的计算分布特征和变量的空间分布特征。另外,通过定制的变异函数,Kriging方法可以自动化地权重调整,这样便可克服通常加权差值方法的差值结果的不稳定性[19]。同时为了解决地层尖灭、透镜体问题,可在算法中对估计值权重系数设置判断函数,来减小插值的均方误差。
在现实地层中,尝尝存在尖灭等特殊地质现象。在建模过程中,当某地层在某处尖灭,可看作在该处该层土的厚度为0,即在此处该层土的层顶高程等于层底高程,该层层面在空间中的表示如图5所示。
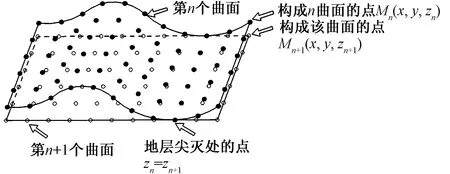
图5 土层尖灭示意图
在地层交界面的插值过程中,插值点与实际勘探孔的空间相关程度表现为实际勘探孔对该插值点的权重系数。p个实际勘探孔p1,p2,…,pn对插值点P0的权重系数分别记为λ01,λ02,…,λ0n,若在勘探孔pi处,存在某层土的层顶高程等于层底高程,则pi处土层厚度为0。当λ0i大于某一阈值t,即pi点与P的空间相关程度到一定程度时,令插值点P在该地层的厚度为0。而pi点附近存在有若干个插值点,pi对所有插值点的权重系数都大于等于阈值t,那么这些插值点相连即得尖灭线。利用该判别条件,三维地质体模型的地层尖灭就出现在勘探孔间,而不在勘探孔处,且阈值可根据不同场地的地形地貌进行调整,可灵活控制建模效果。
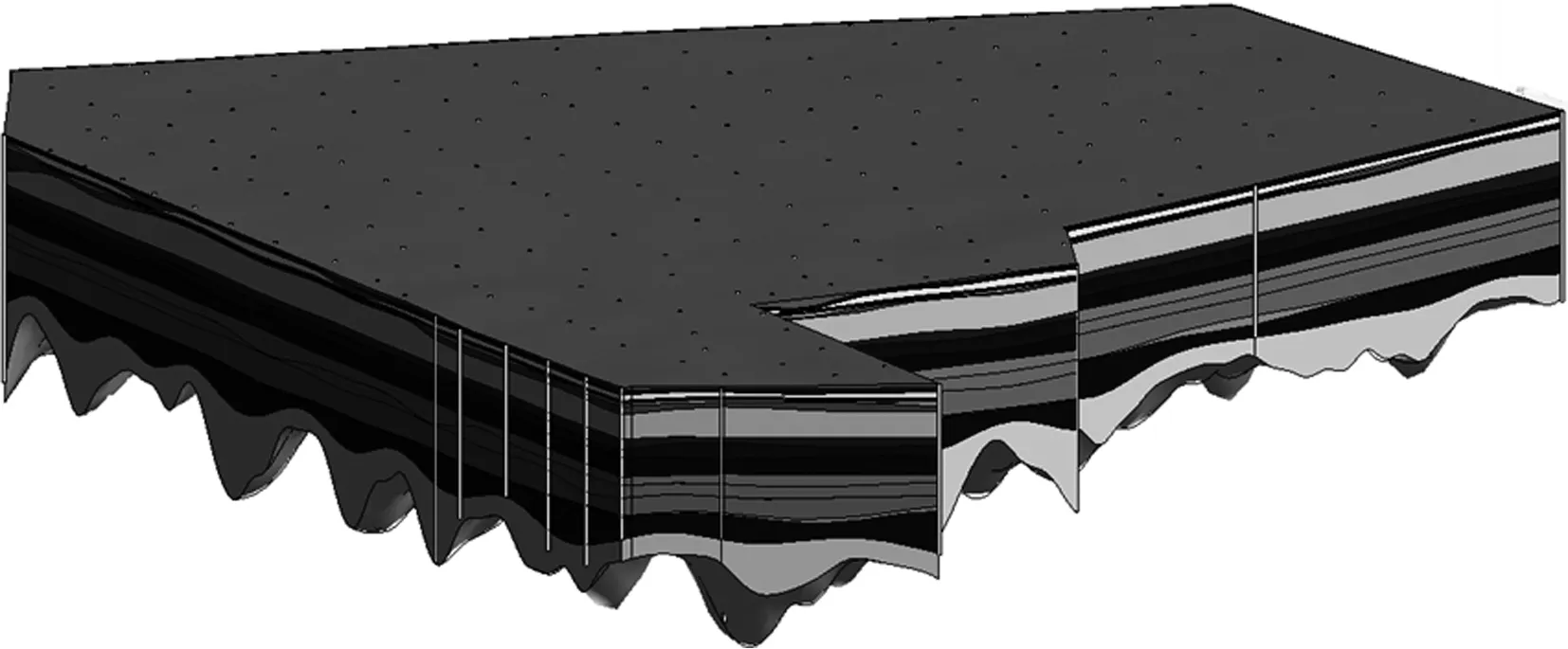
本文研究中以地质体中每层土的构成单个层面的勘探点以Kriging法进行插值,从首层层面到底层层面依次进行计算。为了确保三维地质体模型中的地层曲面之间两两不相交,在插值时需进行条件判断。即遍历构成n面上的点,逐点比较n面上的点Mn的zn值与点Mn+1的zn+1值的大小,若zn 图6 设置克里金插值法的约束面 图7 利用MATLAB实现Kriging插值并进行 曲面矫正 NURBS即为非均匀有理B样条。是一种特殊的样条函数,样条函数只要确定点的位置和互相的距离,就可以表现出一条完整和平滑的曲线。NURBS具有如下特点: 1)非均匀。指曲线的控制点的控制能力可改变,所以曲线的变化可以有密有疏。 2)有理。指该种曲线可以用数学表达式来定义,适合用程序来描述。 3)B样条。利用B样条曲线,曲线由多条曲线构成,使对曲线控制更为灵活。 可见NURBS曲面是一种典型的参数化曲面,可利用点云数据的空间位置实现对其拓扑结构的控制和动态更新。 NURBS为自由曲线曲面提供了统一的数学表达式,使得其形状和解析形式都具有统一的表达式参数[22]。多条NURBS曲线在u、v方向上多次组合,则可构建的一个(p,q)次的 NURBS二次曲面,组成NURBS二次曲面的多条曲线的控制点组合在一起则为(m+1)×(n+1)个控制点构成的控制网格。其表达式为 (1) 式中:Bij为二次曲面模型拟合所需要的控制点;ωij为权重系数;Ni,p(u)、Ni,p(v)分别为u向P阶和v向q阶B样条基函数,按照deboer公式,样条基函数可分别由u向和v向的节点矢量U、V递推而得,节点矢量的表达式为 (2) 式中:节点矢量U和节点矢量V中包含的节点总个数分别为(r+1)个和(s+1)个,r=p+m+1,s=q+n+1。 NURBS曲面的参数通过控制点Bij和权因子ωij描述形状。在以工程勘察数据创建三维地质体模型的过程中,钻孔点数据以及剖面线数据都可以看作为构成各层土层界面上的数据源,但该数据点集不能构造NURBS曲面,而是需要用到反算法求出控制顶点,再用顶点来拟合 NURBS曲面。 NURBS二次曲面的反算就是指构造一张p×q次NURBS二次曲面,该曲面由数据Qk,l,k=0,1,…,m;l=0,1,…,n插值而得[23]。如此一来,二次曲面反算问题便可表示成求解未知控制点Bi,j(i=0,1,…,m+p-1;j=0,1,…,n+p-1)的一个线性方程组。最后二次曲面的 NURBS可由控制点、节点矢量U和节点矢量V高精度拟合而成。 由点云数据生成地层曲面时,受插值算法和生产NURBS曲面算法的制约,生成的地层曲面一般是较为规则的。以上海轨道交通崇明线初勘项目为例,其勘探孔模型,根据点云数据实际生产的地层曲面,如图8所示。部分曲面不在勘探孔的控制范围内,该部分曲面无法准确地模拟真实地层。所以需要在生成的地质体模型时,剔除掉这部分不准确的地层曲面,使得模型能更符合真实地层。 图8 轨道交通崇明线初勘钻孔模型(部分)及 根据点云数据拟合生成的地层曲面 凸包问题简单描述如下:由一组二维平面上的点,求得含有所有点的凸边形,并使得该凸边型最小。采用凸包算法修剪地层曲面的步骤如下: 1)将勘探孔信息所表达的点pi(x,y,z)转为二维平面的点pi(x,y,0)。 2)通过凸包算法,找出这片点云中的凸包点,经由凸包点生成凸包络线。 3)用凸包络线对生成的地层曲面进行修剪,将不准确的地层曲面剔除,留下的部分则为符合真实地形的地层曲面。 凸包算法的具体实现如下: 1)将点二维化。选取构成地层曲面的一组点,记为p1,p2,…,pn,并将其z坐标取零,此时点的三维坐标转为了二维坐标。 2)寻找基准点。遍历所有点,找出含有最小y坐标的点,即P(x,ymin,0),若同时存在多个点具有最小y值,那么取其中横坐标最小的点,使该点为基准点。 3)计算极角。找到基准点与其他点的极角(即过此二点的直线与x轴正方向的夹角,代码中以弧度表示),将这些点按极角的大小正序排列,在极角相同的情况下比较与基准点的距离,离基准点较近的有限。极角的计算方式为 (3) 4)逐点判断。用一个栈(stack)存储凸包上的点,先令基准点和极角排序最靠前的两个点入栈。将排序后的点逐点进行迭代计算,检查栈顶第2个点和该点组成的二维向量n1与栈顶2个点组成的二维向量n2的叉乘是否≥0,即n1在n2的右侧。判断原理为二维平面点乘叉积行列式物理意义,相对于坐标原点,若p1×p2值为正,则p2在p1逆时针方向,若值为负,p2在p1顺时针方向,具体为 (4) 5)若不满足以上条件,则该点暂时入栈。如果满足,则令栈顶元素弹出,并重复上一步的判断过程,直至不满足条件,令此时的点入栈,再对其他点不断执行本步骤。 6)以栈内所有的凸包点生成多段线,对原模型进行切割的布尔运算,便可实现对原地层曲面的修剪。 该工程为上海市闵行区的某住宅勘察项目。根据勘察成果,场地内地表以下65 m深度的土层,其组成部分土类型主要为成层分布的软弱黏性土、粉土及砂土。根据勘察成果,场地土层可分为18个土层,各土层物理力学性质差异明显,且①1、①3、②1、②3-1、③1、③1t、⑦1t都是局部缺失,场地存在大量尖灭地质现象。由于③1t的存在,本场地内自上而下还存在重复的③1层。该工程的勘探孔具体数据见表1。 表1 勘探孔数据 将数据导入MATLAB进行插值计算。由于本工程存在203个真实钻孔,为了更好模拟钻孔间的土层趋势,在进行Kriging法插值时,选用2 500个插值点,并且将计算后的数据导出。再根据曲面边界条件整理数据,得到处理后的插值数据。将插值数据与原始数据整合导入Dynamo二次开发程序中,先通过插值数据生成点云,再由点云生成NURBS地层曲面,然后用凸包算法搜索剔除勘探孔控制范围外的地层曲面。利用余下的地层曲面建立三维地质体模型。模型切割效果和勘探点平面布置如图9所示。结合图9可看出,模型平面形状与本项目勘探孔控制区域一致。最后再导入物理力学性质参数,整体三维地质BIM模型则建立完成,最后完成的模型如图10所示。 图9 三维地质模型与二维平面图的比较 图10 三维地质体模型 模型中⑦1层层底起伏较大,该层底层标高为-34.54~-25.87 m,层厚为1.9~9.7 m。将其他土层隐藏,易观察该层的土层分布,如图11所示。图上所示最上的蓝色土层即为⑦1层,其下淡紫色土层为⑦1t层,该层仅在局部分布。由模型可得,⑦1t层厚度较厚处,⑦1层层厚较薄,且层底标高较高,且模型展示的⑦1t层尖灭现象与勘察报告中剖面图一致。当在该模型中引入桩基模型时,根据桩底标高,易观察该桩端是否穿过了该持力层。 图11 隔离体的三维模型 目前BIM在勘察领域中的应用较少,市场上存在许多地质体建模软件,常规快速建模的方法在建模过程中会牺牲掉一部分模型精度,如果依靠技术人员经验或其他人机交互的方法则会提高建模的工作量。本文从数据提取、地质曲面的生成、地质模型的矫正3方面进行处理,在确保建模精度的情况下实现快速建模。 1)梳理了对于复杂地形建模数据处理的逻辑,建立统一所有勘探孔分层的母版土层层序,应用方法解决在建模过程中地质界面错连和插值过程数据不匹配。 2)通过带条件的Kriging方法对勘探孔源数据进行插值,然后由Dynamo自编节点实现用整合后的点云数据拟合NURBS曲面,保证了模型数据点和模型地质界面的精度,解决了复杂地地质体的建模难点。 3)由Dynamo自编节点实现凸包算法修剪地层曲面,剔除了不准确的地层曲面,利用剩下的地层曲面完成参数化三维地质体模型建立。建模过程迅速,有效地减少了人机交互,在勘探孔参数发生变化时,模型能够快速进行更新,大大提高了已建模型修改重建的效率。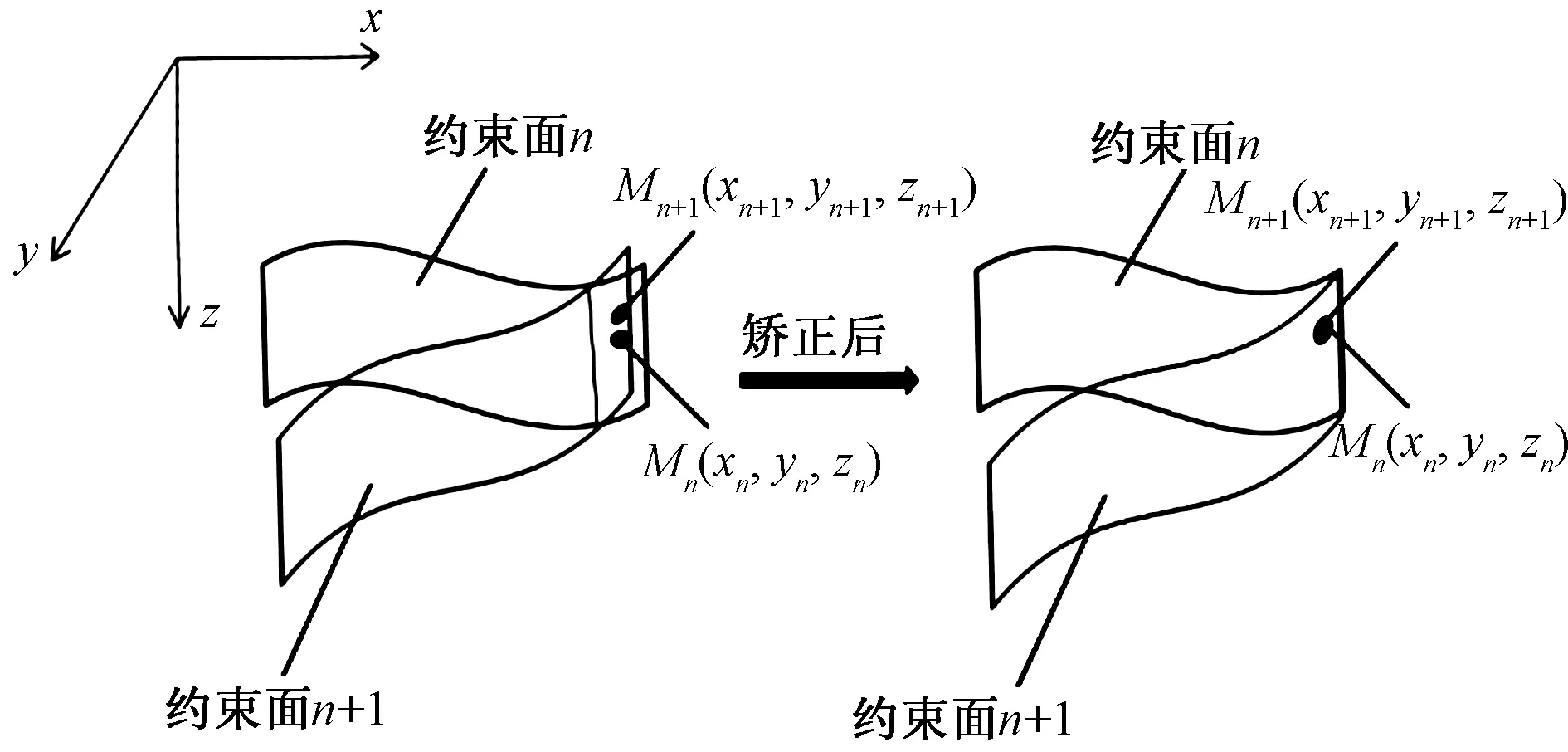

2.3 基于NURBS建立地层曲面
2.4 基于凸包算法修剪地层曲面

3 工程实例



4 结论

