基于自适应KF 动态虚拟陀螺数据融合算法的研究

熊泰然，陈雯雯，陈宏宇，高海云，吉言超

（1.中国科学院 微小卫星创新研究院，上海 201210；2.中国科学院大学 电子电气与通信工程学院，北京 100049；3.上海科技大学 信息科学与技术学院，上海 201210）

0 引言

在惯性导航系统中，陀螺仪是测量移动物体角速率的关键传感器，光纤陀螺被广泛使用在传统卫星中。而卫星的小型化逐渐成为一种发展趋势，由于微机电系统（Micro-Electro-Mechanical System，MEMS）技术的快速发展，微小卫星的技术升级出现了更多可能。MEMS 器件具备很多优点，比如体积小、功耗低、成本低，更适合微小卫星集成化、模块化、研制周期短的设计要求。但是MEMS 传感器的精度一般较低，无法满足特定条件下的精度需求。

为了提高MEMS 陀螺仪的精度，目前有一些针对单个陀螺仪的滤波算法研究，比如使用神经网络等算法，算法普遍较为复杂，对于单个陀螺的处理也难以大幅提升精度。同时也有一些新型陀螺仪进行在轨验证，比如半球谐振陀螺。BAYARD 等在2003 年最先提出了一种虚拟陀螺技术，该技术使用卡尔曼滤波（Kalman Filter，KF）算法，融合了4 个相同的MEMS 陀螺仪的数据，通过实验证明了方法的可行性，但精度仍然有提升空间。国内外也有一些在此基础上进行的改进研究，比如改进滤波算法，增加陀螺数量，或者改用异方差模型建模等方法，算法由于模型参数的固定性，仅在静态条件下或者仅在动态条件下能够显著提升精度，难以保证在静态和动态条件下都有良好的性能。尤其是在角速率变化较快的情况下，卡尔曼滤波器的参数对滤波效果有较大影响。为了解决这个问题，采用多模型滤波算法动态调整是有效的解决方法，但是与KF 相比，仍然存在算法计算量太大的问题。

本文针对陀螺仪的静态和动态特性，提出一种自适应的KF 算法，在不同条件下自动调整模型参数，尤其在角速率变化较快的动态条件下可以保证滤波效果，通过搭建6 个陀螺仪组成的硬件平台进行转台实验，验证算法的有效性

1 陀螺仪模型分析

本章选取单个陀螺仪的输出进行噪声分析，并对陀螺仪进行建模。MEMS 陀螺仪中随机误差的主要来源之一是陀螺仪输出的白噪声，通过对角速率积分，该测量噪声的影响被累积，角速率测量白噪声表现为角度随机游走（Angular Random Walk，ARW）。大多数情况下，精确测量角度比测量角速度更为重要，这使得该测量噪声的影响更加明显。MEMS 陀螺仪误差的另一个主要来源是由于陀螺仪偏置的微小变化，随时间的变化随机游动。这种误差为速率随机游走（Rate Random Walk，RRW）。MEMS 陀螺仪的一般模型表示如下：

式中：

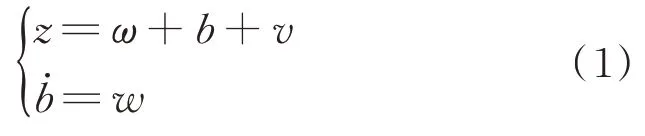
z

为陀螺仪输出；

ω

为真实角速率；

b

为白噪声

w

驱动的缓慢变化的偏置误差；

v

为测量白噪声。

Allan 方差分析法是被国际普遍接受的一种表征速率传感器随机噪声过程的分析方法。Allan方差分析的主要结果是Root Allan 方差图，通过该图可以识别捕获数据中存在的随机噪声过程的类型和大小。本文使用6 个MPU6050 陀螺仪进行实验，对单个陀螺仪采集4 h 静态数据的Allan 方差分析，如图1 所示。

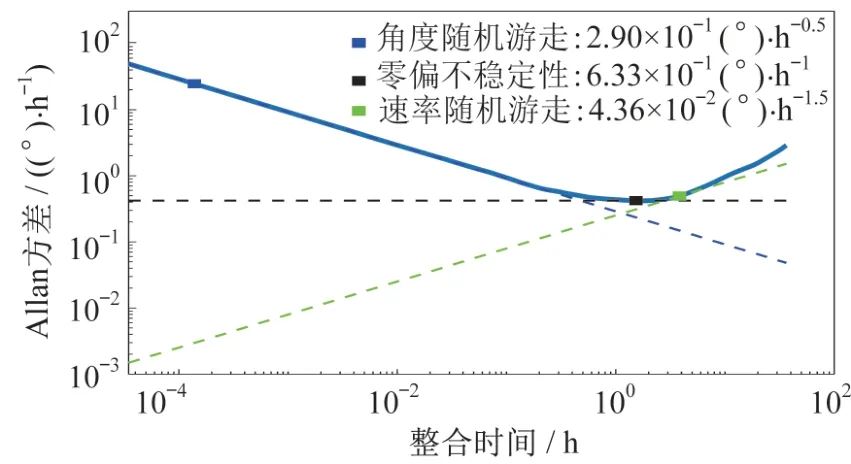
图1 单MEMS 陀螺Allan 方差分析Fig.1 Allan variance analysis of the single MEMS gyroscope

根据Allan 方差分析结果可知，陀螺的主要误差来源为角度随机游走和零偏不稳定性，速率随机游走误差对陀螺精度影响较小。

对陀螺噪声进行进一步分析，首先对噪声的分布拟合，如图2 所示，根据拟合结果，陀螺的噪声可以近似拟合为正态分布；然后对陀螺噪声的相关性进行分析，如图3 所示。

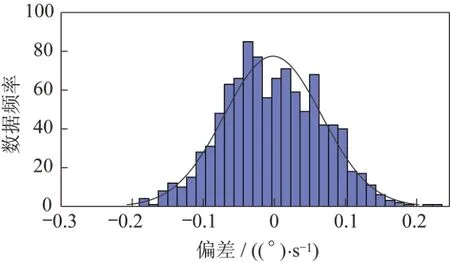
图2 单MEMS 陀螺噪声分布拟合Fig.2 Noise distribution fitting of the single MEMS gyroscope

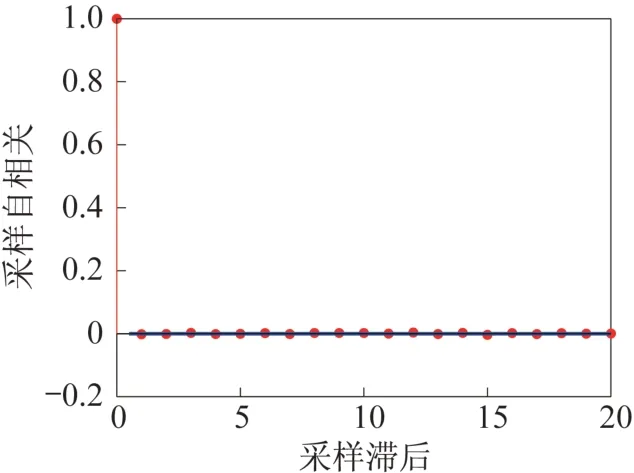
图3 单MEMS 陀螺相关性分析Fig.3 Correlation analysis of the single MEMS gyroscope

根据图3 分析可知，自相关曲线在起点显示1个峰值，而后快速地下降到零，显示没有相关性，也没有周期性。同时，为了降低算法复杂度，

b

不参与周期性和相关性分析，陀螺仪的模型可以简化为

2 自适应卡尔曼滤波器设计

2.1 状态空间模型

建立离散卡尔曼滤波器，需要先建立状态空间的测量模型和预测模型，根据式（2）的陀螺仪误差模型，并且由于本文实验使用6 个陀螺仪的组合阵列，可以得到卡尔曼滤波器的测量模型为

式中：

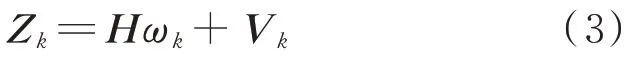
式中：

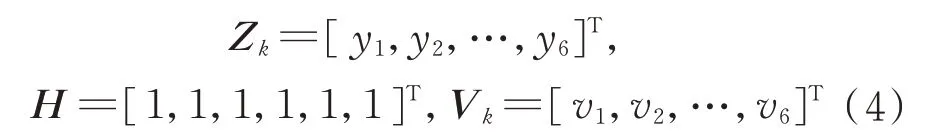
w

为陀螺仪的真实角速率，6 个陀螺均相同；

Z

为陀螺仪阵列的输出测量矩阵；

H

为测量转换矩阵；

V

为测量噪声矢量，且测量噪声的期望为零。令陀螺噪声的协方差矩阵为

R

，由于每个陀螺仪之间如存在工艺或者环境等方面的一致性，即使是在单个硅晶片上制造的陀螺仪阵列中存在的相关因子，也无法精确获得，但是为了分析相关性对精度提高的影响，假设陀螺之间存在相关性。所以

R

矩阵不是对角阵，存在非对角线元素。这里假设在相同分量的陀螺仪之间存在恒定的互相关，则矩阵

R

可以表示为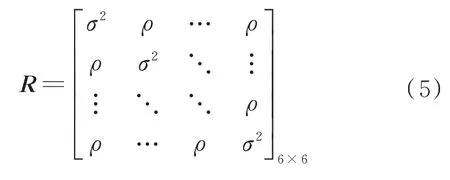

式中：

σ

为陀螺的噪声方差；

ρ

为恒定的相关系数。

在用于表示平稳时间序列信号的许多标准模型中，最常用的是AR 模型，AR 模型能够较好地体现出噪声的动态变化。AR 建模过程包括3 个迭代步骤：模型识别、参数估计和检查诊断。为了降低整体算法的计算量，本文使用模型如下：

式中：

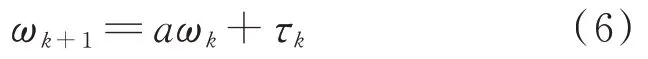
a

为模型参数；

τ

为预测模型的白噪声。

根据式（6），可以得到卡尔曼滤波器的状态空间预测模型为

式中：

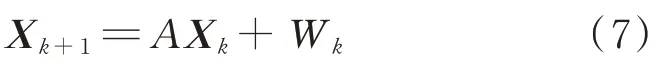
X

为系统的状态矩阵；

A

为预测模型参数，且

A

=

a

；

W

为系统噪声，期望为

q

=0，方差为

Q

。

2.2 卡尔曼滤波器改进

根据建立的陀螺仪状态空间测量模型和预测模型，可以得到标准的离散卡尔曼滤波器方程，预测模型状态预测为

预测方差更新为

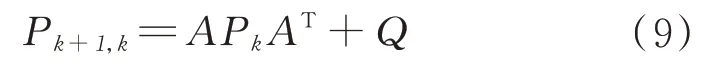
求解滤波增益为

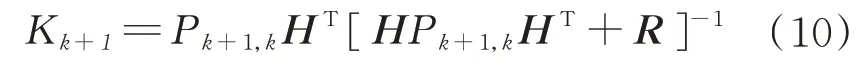
状态最优估计为

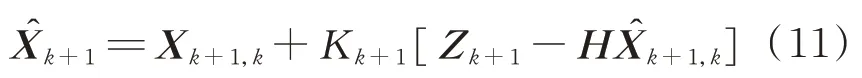
最优估计方差更新为

设计卡尔曼滤波器时，选取不同的参数会改变滤波器的性能，在静态条件下，卡尔曼滤波器可以通过调整参数大幅提升陀螺的性能。在滤波器中，

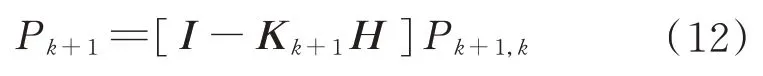
Q

矩阵为预测模型的方差，

R

矩阵为测量模型的方差，

Q

矩阵小，则认为预测模型较测量值相比更准确，系统更信任模型的预测值。但是，在实际使用时，不同的动态条件下使用固定参数无法保证滤波效果，特别是角速率变化较快时。在这种条件下，滤波器的跟踪性能显著下降，因此可以通过增加反馈来实现自适应卡尔曼滤波器，动态地调整

Q

矩阵和

R

矩阵的大小，提升系统的性能。由于

Q

矩阵和

R

矩阵的相对大小就可以影响卡尔曼增益的大小，所以为了减小计算量，选取维度更低的

Q

矩阵进行自适应调节，对于

Q

矩阵来说，动态条件下模型误差增大，通过反馈可以更好地改善动态性能，为了不影响静态性能，在反馈中可以引入Sigmod函数：

在机器学习中，Sigmod 函数通常作为神经网络的激活函数被广泛使用。通过引入Sigmod 函数，在变化较快的动态条件下，发挥自适应调节反馈的功能，提升动态性能，同时不对静态条件的滤波造成影响，使不同条件下的参数变化平滑过渡。改进的离散自适应卡尔曼滤波器（S-Kalman Filter，SKF）方程可以表示如下。

生成放缩平移调整的Sigmod 函数为

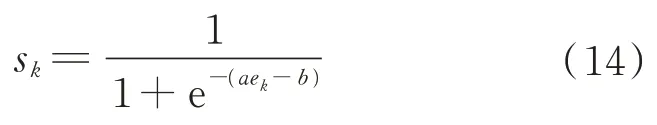
预测模型状态预测为

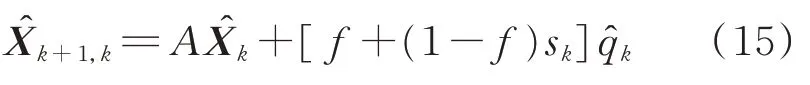
预测方差更新为

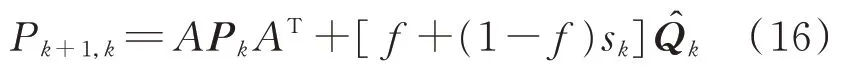
求解滤波增益为

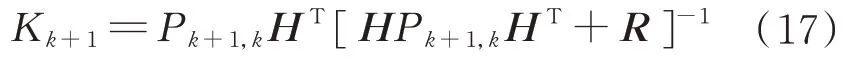
状态最优估计为

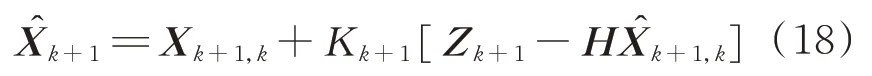
最优估计方差更新为

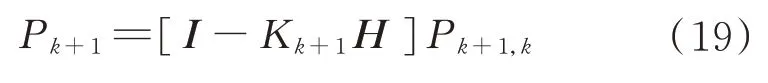
反馈计算为

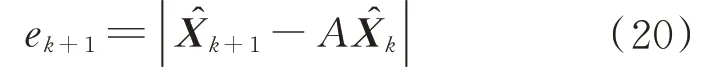
偏差更新为

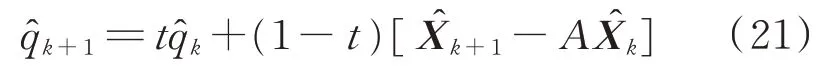
方差更新为

式中：

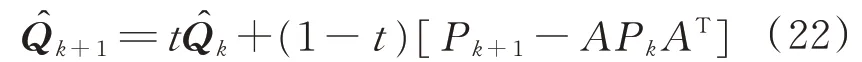
a

、

b

为Sigmod 函数的缩放和平移系数；

f

为反馈因子；

t

为跟踪因子，与标准卡尔曼滤波相比，SKF 改进了静态和动态的性能，更适合陀螺仪的滤波算法处理。

3 实验及结果分析

搭建陀螺阵列进行实际测试，MEMS 陀螺仪使用6 个MPU6050，主控芯片使用STM32，设计原理图并制作PCB 电路板，如图4 所示。

图4 陀螺仪阵列PCB 板Fig.4 Gyroscope array PCB board

与卫星通信时使用CAN 总线接口，本文中实验使用STM32 的SPI 接口进行通信，所有实验均在相同的外部环境下进行测试，室温为25 ℃，使用高精度转台（0.000 01（°）/s）进行实验测试。由于转台的精度比MEMS 陀螺仪的精度高出几个数量级，因此，转台的角度率可以认为是真实角速率，先在静态条件下测试，然后在加入简谐波的动态条件下进行测试，最后加入人造信号进行角速率变化较快的动态测试，验证算法的可行性。使用的转台如图5 所示。

图5 转台测试Fig.5 Turntable test

3.1 静态滤波结果

首先在静态条件下进行测试，在陀螺仪开始工作后求取一定时间内的稳态误差，并在程序上做处理，加和求平均值；然后减去均值消除稳态误差的影响，以50 Hz 的采样频率采集6 个陀螺仪的数据，分别使用平均值算法、标准卡尔曼滤波算法和自适应卡尔曼滤波算法进行滤波处理；最后分别对比6个陀螺的输出数据、SKF 算法的滤波数据，以及不同算法滤波的效果对比，得出的实验结果如图6 和图7 所示。

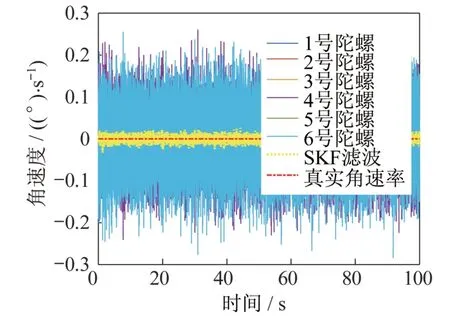
图6 静态条件SKF 算法Fig.6 SKF algorithm under the static condition

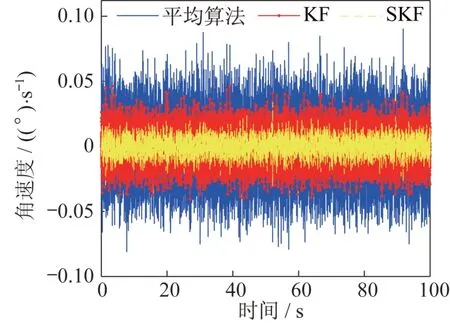
图7 静态条件不同算法对比Fig.7 Comparison of different algorithms under the static condition

对使用不同算法得到的虚拟陀螺静态数据分别计算Allan 方差，与单MEMS 陀螺仪的Allan 方差进行对比，画出Allan 方差图，得到的对比结果如图8 所示。

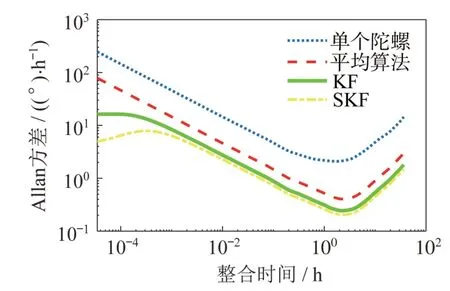
图8 Allan 方差对比Fig.8 Allan variance comparison

对于静态条件下的Allan 方差进行分析，3 种算法均能降低陀螺的噪声，KF 算法和SKF 算法对噪声的过滤性能更好。最后计算了静态条件下滤波后的数据残差的方差，与Allan 方差计算得到的ARW 和零偏不稳定性分别进行效果对比，结果见表1。

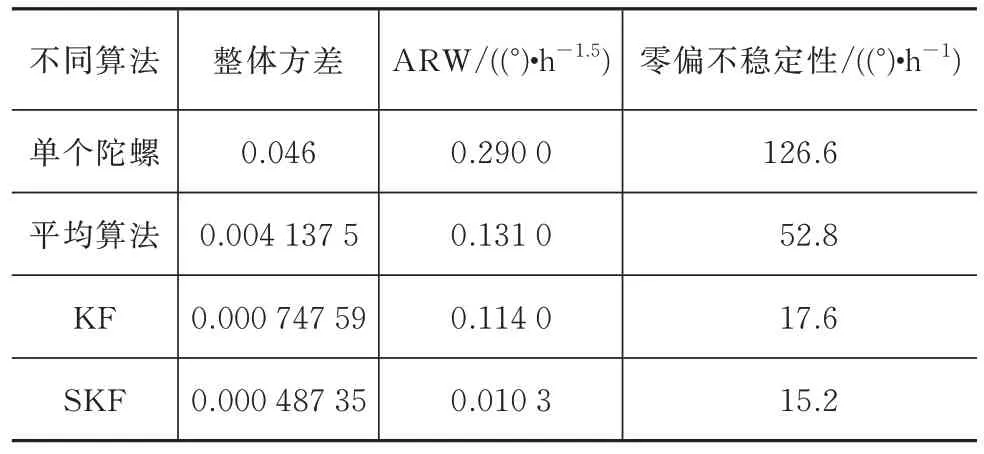
表1 整体方差、ARW、零偏不稳定性对比Tab.1 Comparison of overall variance，ARW，and zero bias instability

由实验数据可知：静态条件下标准KF 实现的虚拟陀螺，数据残差的方差可以降低为单个陀螺的1/62；而SKF 算法实现的虚拟陀螺，数据残差的方差可以降低为单个陀螺的1/94，静态条件下小幅优于标准卡尔曼滤波，算法可以显著提升陀螺的精度。

3.2 动态滤波结果

对于动态滤波，首先在加入简谐波的条件下进行测试，这里为了对比静态和动态下的不同效果，令标准卡尔曼滤波器和自适应卡尔曼滤波器与静态条件下的参数保持一致；然后分别求出不同算法滤波后的残差进行对比。在简谐波的动态条件下，得到的实验结果如图9 和图10 所示。

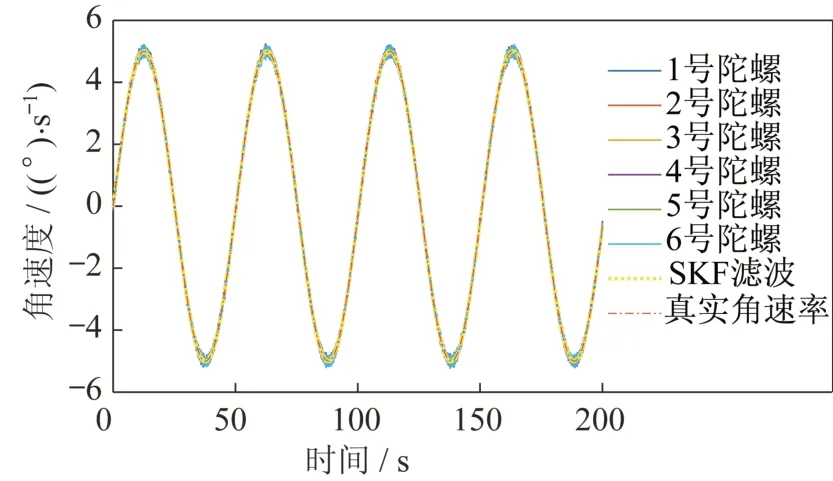
图9 动态条件SKF 算法Fig.9 SKF algorithm under the dynamic condition

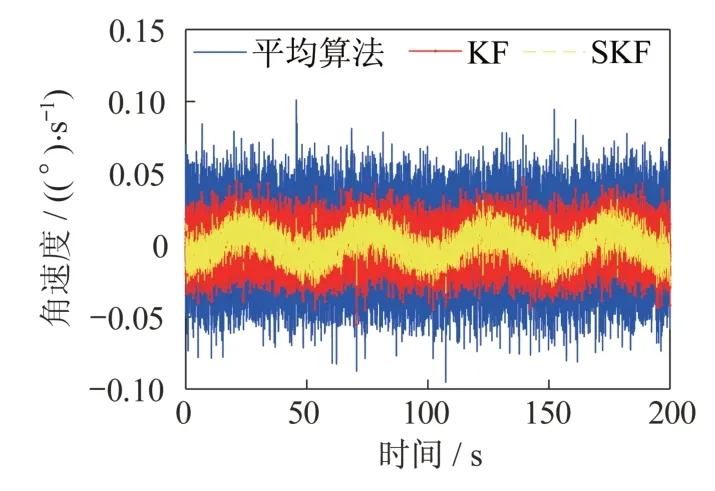
图10 动态条件不同算法对比Fig.10 Comparison of different algorithms under the dynamic condition

简谐波的变化比较平缓，由计算可得，简谐波经过KF 算法滤波后，残差的方差为1.351 9×10，方差为单个陀螺的1/36；SKF 滤波后，残差的方差为1.049 9×10，方差为单个陀螺的1/47。SKF 算法与标准KF 算法相比，精度更高，但提升的精度不明显。为了测试变化较快的动态条件下的效果，加入角速率突变的人工信号，对比测试不同算法的滤波性能，同时计算残差对比效果，实验结果如图11和图12 所示。

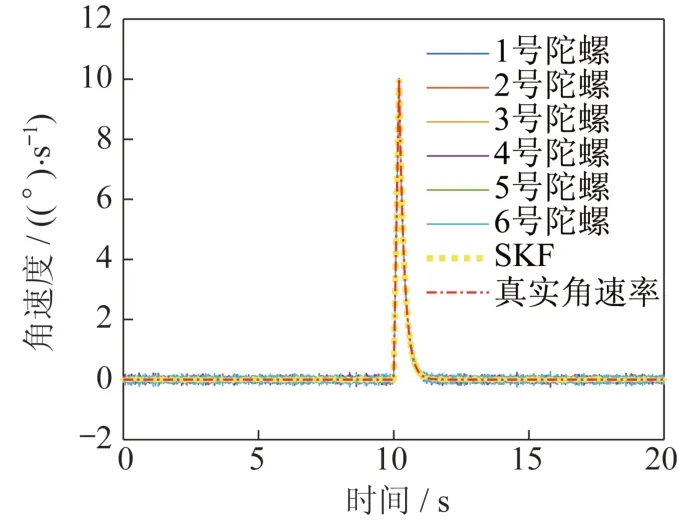
图11 特殊动态条件SKF 算法Fig.11 SKF algorithm under the special dynamic conditions

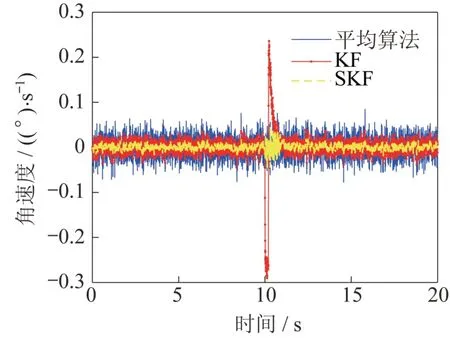
图12 快速动态条件不同算法对比Fig.12 Comparison of different algorithms under the special dynamic condition

在这种动态条件下，由实验数据可知，在滤波器参数保持不变时，快速动态条件下标准KF 算法的滤波效果难以保证，标准KF 算法无法识别快速变化的噪声，跟踪性能大幅下降；而自适应卡尔曼滤波器通过不同权重的反馈调节，仍然可以大幅提升陀螺的精度，保持良好的跟踪性能；最后根据实验数据分别计算不同算法滤波结果残差的方差，对比见表2。

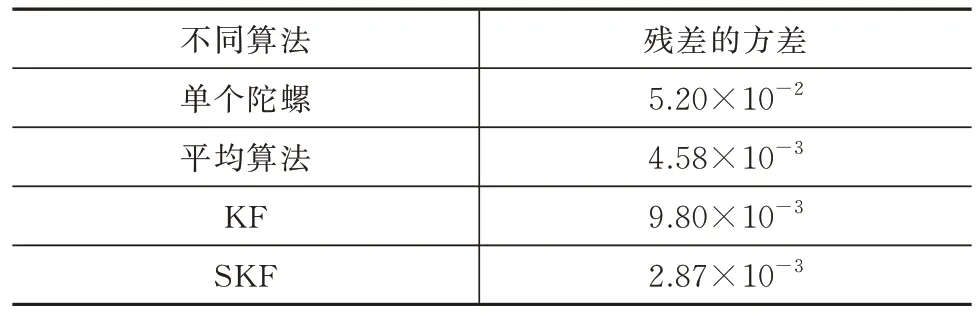
表2 残差的方差对比Tab.2 Comparison of residual variance

根据表中数据可知：在对快速变化的数据进行滤波时，KF 算法效果较差，残差的方差仅为单个陀螺的1/5；而使用SKF 算法，数据残差的方差可以降低为单个陀螺的1/18。

4 结束语

为了减小MEMS 陀螺仪噪声的影响，本文研究了多MEMS 陀螺融合的虚拟陀螺技术，通过Allan方差等方法分析了陀螺的噪声，通过分析卡尔曼滤波器的参数对陀螺静态动态性能的改善特点，有针对性地提出了一种自适应的卡尔曼滤波器，以优化陀螺仪的静态和动态性能。对于快速变化的数据，SKF 算法优势明显。通过搭建的硬件平台进行实验测试，验证了算法的正确性，但仍然存在不足，提出的算法的参数比标准卡尔曼滤波算法更多，虽然滤波效果更好，但是在实际使用时更依赖参数的调节，增加了不便性，后续将继续优化算法的复杂度。