地球同步卫星BSR 硅太阳电池阵输出功率衰减规律分析

刘 帆，郭 静，郭小红，黄晓峰

（航天器在轨故障诊断与维修重点实验室，陕西西安 710043）

0 引言

自1973 年3 月我国首次在实践一号科学试验卫星上成功使用国产硅太阳电池阵以来，硅太阳电池阵在光电转换效率、输出功率、电池阵面积和布片效率等方面取得了长足的进步。由于地球同步卫星在轨运行寿命一般在8 a 以上，每年的全光照期约为272 d，太阳电池阵长期受粒子辐射、紫外辐射和冷热交变等因素影响，其输出功率会出现缓慢且趋势明显的衰减现象。掌握太阳电池阵在轨性能衰减规律不仅有助于改进功能设计，而且可以用于优化卫星在轨运行管理策略。文献［2］基于遥测数据，分析了背表面场反射（Back Surface Field Reflection，BSFR）硅太阳电池阵输出电流近6 a 在轨运行期间的衰减情况。文献［3］对我国自主研发的某类浅结、密栅硅太阳电池阵在轨输出功率衰减率进行了分析。

本文以某地球同步卫星使用的n+/p 型浅结、密栅、背表面反射（Back Surface Reflection，BSR）硅太阳电池阵为研究对象，通过修正太阳电池阵输出功率计算结果，并采用非参数回归方法中局部加权回归散点平滑法（Local Weighted Scatterplot Smoothing，LOWESS）分析了其在全设计寿命期间的功率变化规律。据此建立统计预测模型，用于硅太阳电池阵超寿运行期间的性能预测。

1 硅太阳电池阵输出功率计算方法

参照文献［2-7］，太阳电池阵输出功率

P

为太阳电池阵输出电压

V

和输出电流

I

的乘积，太阳电池阵输出电压

V

的计算公式为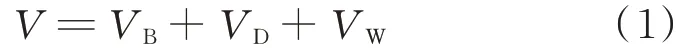

式中：

V

为母线电压；

V

为隔离二极管正向电压降；

V

为太阳电池阵与负载或蓄电池组之间线缆电压降。太阳电池阵输出电流

I

的计算方法与卫星电源分系统组成结构相关。文中所分析卫星采用双独立部分调节顺序线性母线，其电源分系统的基本组成结构如图1 所示。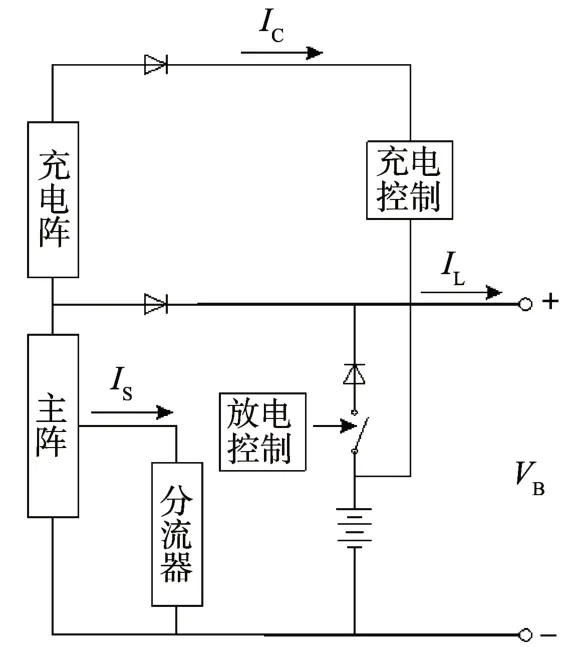

图1 电源分系统组成结构Fig.1 Structure chart of the power subsystem

结合卫星下传遥测参数，太阳电池阵输出电流

I

的计算公式为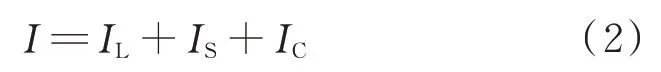

式中：

I

为负载电流；

I

为分流电流；

I

为充电电流。

本文选取某卫星8 a 设计寿命期内遥测数据，依据式（1）和式（2）计算得出BSR 硅太阳电池阵在每天12 时的最大输出功率。输出功率值的归一化结果如图2 所示。

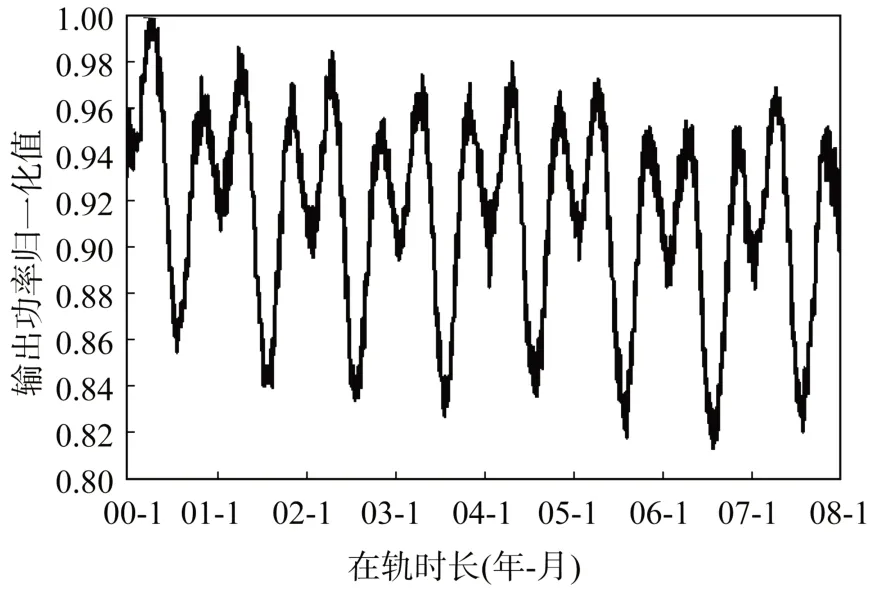
图2 BSR 硅太阳电池阵输出功率曲线Fig.2 Output power curve of the BSR silicon solar array

图2 中，太阳电池阵输出功率变化呈现马鞍形曲线或双峰曲线形态，年周期性变化特征明显。其中，峰值出现在每年的春分点和秋分点附近，鞍点出现在冬至点附近，最小值出现在夏至点附近，整体呈缓慢下降趋势。根据该硅太阳电池阵设计方案，寿命末期时的秋分点相对寿命早期输出功率衰减17.6%，而夏至点输出功率将衰减16.0%。但是通过对图2 中实测数据进行核算，寿命末期时的秋分点实际输出功率比寿命早期仅下降5.0%，夏至点输出功率比寿命早期也仅下降了4.5%，由此可知，该太阳电池阵留有相当大的设计裕度。

2 BSR硅太阳阵输出功率衰减规律分析

2.1 硅太阳电池阵输出功率修正

为分析硅太阳电池阵输出功率衰减规律，需要对输出功率的光强因子和温度因子进行修正，这里参照文献［12］中静止轨道1 m太阳电池阵面积寿命初期输出功率估算公式：

式中：

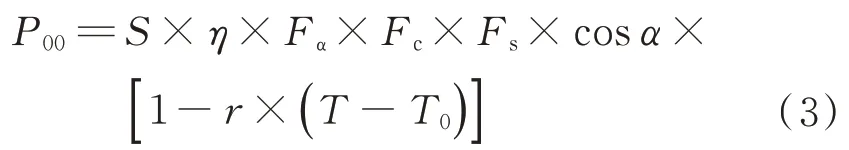
P

为1 m太阳电池阵面积寿命初期输出功率；

S

为空间太阳常数光强；

η

为太阳电池光电转化效率；

F

为太阳电池阵组合损失因子；

F

为太阳电池阵布片效率；

F

为日地距离因子；cos

α

为太阳光与太阳电池阵法线方向的夹角余弦值；

r

为太阳电池阵功率温度系数，硅太阳阵参考值为4.5‰；

T

为太阳电池阵轨道工作温度；

T

为标准条件下测试温度，即25 ℃。由式（3）可知，

S

、

F

、

F

可视为常值，

η

虽存在长期衰减现象，但由于可纳入太阳电池阵输出功率的总衰减效应，故可作为常值使用；余下的

F

×cos α即为光强修正因子

F

，［1-

r

×（

T

-

T

）］为温度修正因子

F

。

本文使用STK 软件获取ECIVVLH 坐标系下的太阳相对于卫星的方位、俯仰和斜距信息：

式中：

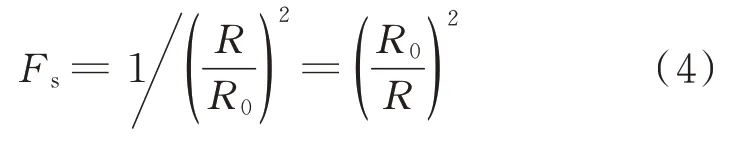
R

为日地距离常数；

R

为卫星到太阳的斜距。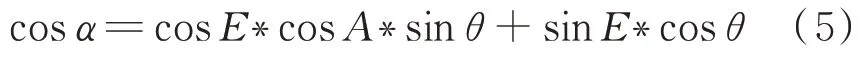

式中：

A

为太阳方位角；

E

为太阳高度角；

θ

为帆板转角。故光强修正因子

F

计算公式如下：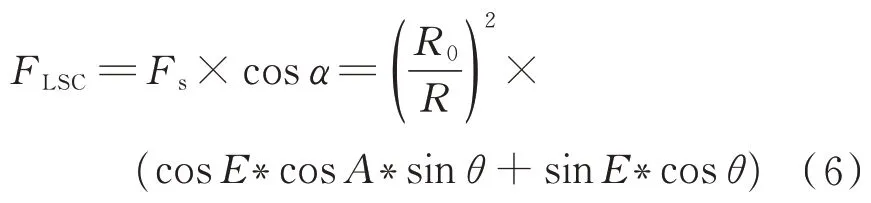

温度修正因子

F

计算公式如下：

光强修正因子

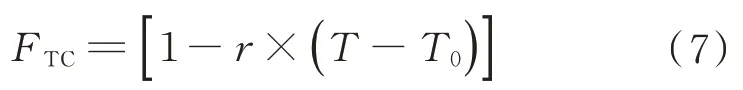
F

计算结果如图3 所示，以a 为周期，光强修正因子变化曲线与输出功率类似，在0.878～0.998 之间变化，整体变化趋势保持平稳。

图3 光强修正因子Fig.3 Curve of the light intensity correction factor

温度修正因子

F

计算结果如图4 所示。图中，温度修正因子整体呈缓慢下降趋势，峰值出现在每年的夏至点和冬至点附近，且在夏至点附近值最大，最小值出现在春分点和秋分点附近。

比较图3 和图4 可知，光强修正因子和温度修正因子在同一时刻的变化方向相反。依据温度修正因子与光强修正因子绘制的散点图，如图5 所示。统计结果显示，温度修正因子与光强修正因子的相关系数为-0.977，统计特性显著，两者之间具有较强的负相关关系。

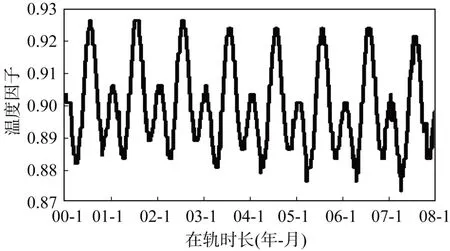
图4 温度修正因子Fig.4 Curve of the temperature correction factor

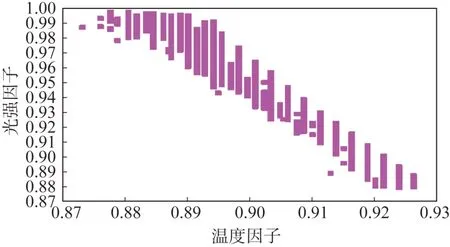
图5 光强修正因子与温度修正因子散点图Fig.5 Scatter plot of the light intensity correction factor and the temperature correction factor

依据式（3）～式（7），可以得出硅太阳电池阵输出功率修正值计算公式如下：

式中：

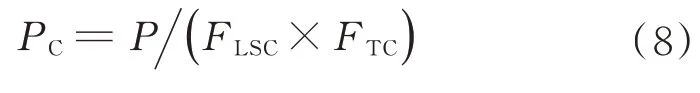
P

为硅太阳电池阵输出功率；

P

为输出功率的光强和温度联合修正值。

硅太阳电池阵输出功率的修正结果如图6 所示。图中，红色散点为输出功率归一化值，黑色实线为其修正值。对比可知，修正功率相对输出功率幅值增大，波动范围相对缩小，其曲线形态也为马鞍型曲线，且其变化周期与输出功率基本一致。

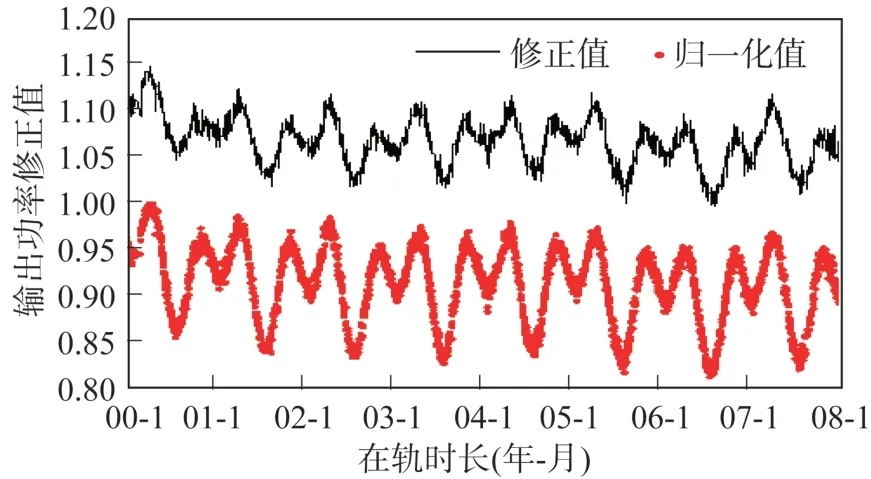
图6 硅太阳电池阵输出功率修正曲线Fig.6 Correction curve of the silicon solar array output power

2.2 硅太阳电池阵输出功率衰减规律

目前，分析硅太阳电池阵输出功率衰减规律，通常采用的方法是在完成太阳电池阵输出功率修正后，使用二分点或二至点等特定时刻的功率数据，通过多项式拟合或指数函数拟合等参数回归（Parametric Regression，PR）分析方法，提取出衰减趋势信息。此类方法存在以下2 个缺陷：

1）使用特定时刻的输出功率数据分析衰减规律，相当于对原始分析数据进行了再次抽样。这种方法使分析数据量大为减少，衰减规律变得易于提取，但是由于舍弃了大量有效信息，所获取衰减规律与实际衰减情况存在一定的偏差，且易受野值点、离群点等异常数据的影响。

2）参数回归分析方法一般首先需要对数据模型进行假设，如多项式形式或指数函数形式，再估计其中的参数。虽然这些假设模型一般基于理论或前人的研究，但是由模型误设导致的设定误差（Specification Errors，SE）仍不可避免。

针对上述问题，较为合理的解决方法就是通过系统性的探索数据来找到衰减曲线，即非参数回归方法（Non-parametric Regression，NR）。NR 并不需要预设函数形式，而是通过使用样本数据，根据分组后的自变量计算因变量的平均值，并平滑成一条曲线。这条曲线用一种更加精细的方式来描述自变量与因变量之间的函数关系，本文采用的是最常用的LOWESS。

LOWESS 是取一定比例的局部数据，在这部分子集中拟合多项式回归曲线，通过数据子集加权残差平方和最小，以此得出数据在局部展现出来的规律和趋势。LOWESS 使用的拟合多项式如下：

式中：（

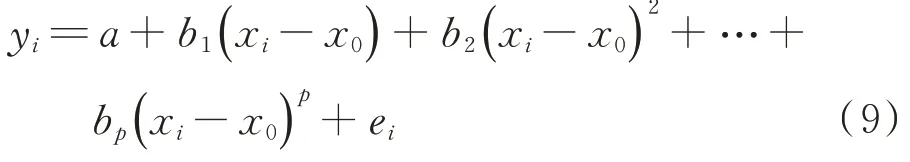
x

，

y

）为局部子 集中的数据 样本点

i

；

x

为局部子集的焦点；

e

为数据样本点

i

的拟合残差；

a、b

为多项式系数；

p

为多项式阶数。

LOWESS 回归结果如图7 所示。图中，散点为硅太阳电池阵输出功率修正值，实线为依据功率修正值得到的LOWESS 回归曲线。依据LOWESS回归曲线计算得出，该硅太阳电池阵在轨运行8 a 期间，输出功率下降了4.15%，与图1 显示的秋分点和夏至点的在轨输出功率衰减情况接近，但衰减速率略为降低。由此可知，仅采用二分点或二至点等特定时刻功率数据易产生衰减偏大的问题。

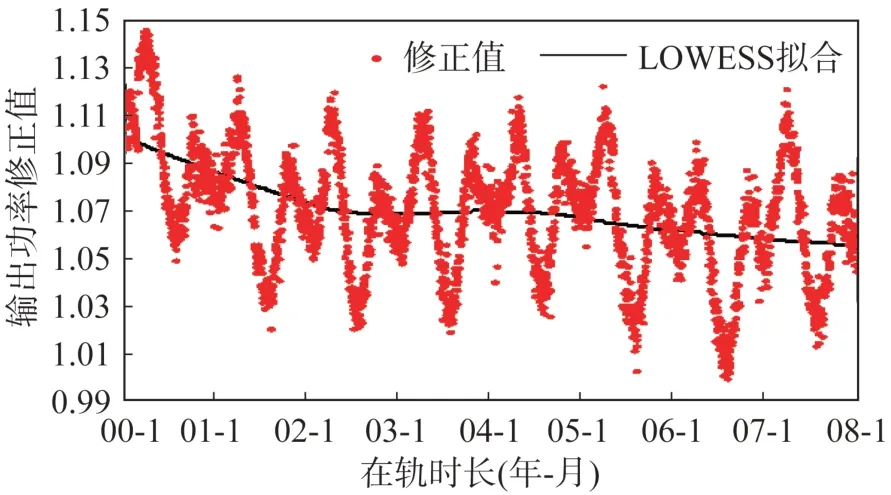
图7 输出功率修正值的LOWESS 回归曲线Fig.7 LOWESS regression curve of the corrected output power

此外，图7 中输出功率的衰减趋势呈现出阶段性变化的特点：1）卫星转入在轨运行阶段至第2 年7 月份为快速衰减期，年均衰减率约为1.15%；2）在轨第2 年7 月份至第4 年7 月份为平稳变化期，年均衰减率基本为0%；3）在轨第4 年7 月份至第8 年为缓慢衰减期，年均衰减率约为0.37%。

作为对比，这里使用3 阶多项式拟合模型提取输出功率的衰减趋势信息，如图8 所示。

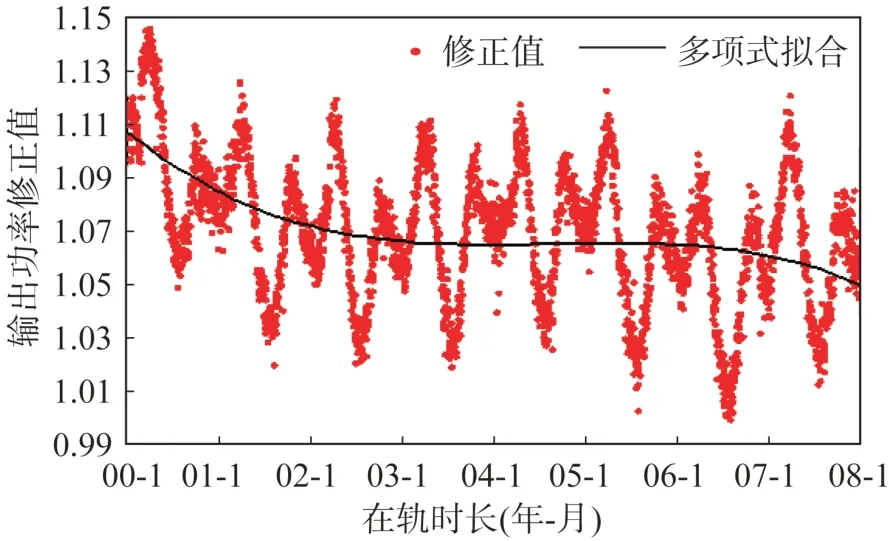
图8 输出功率的3 阶多项式拟合曲线Fig.8 Third-order polynomial fitting curve of the output power

图8 显示卫星转入在轨运行阶段至第3 年初为快速衰减期，第3 年至第6 年初为平稳变化期，第6 年初至第8 年为缓慢衰减期。由此可知，3 阶多项式拟合模型虽较为平滑，但受限于模型设定误差，不仅快速衰减期和平稳变化期被延长，且缓慢衰减期的衰减速度呈现出逐步增大的趋势，在预测未来变化趋势时不可避免地出现估值过低的问题。

3 基于LOWESS 曲线的硅太阳阵输出功率预测方法

文中获取的LOWESS 回归拟合结果不仅可以用于揭示硅太阳电池阵输出功率衰减规律，也可应用于预测硅太阳阵输出功率。其思路较为简单，就是通过拟合LOWESS 回归结果构建长期预测模型，并使用历史的LOWESS 回归残差作为长期预测模型的预测残差，将模型预测值与预测残差相加得到最终的预测结果。

本文使用硅太阳电池阵在轨运行第8 年的输出功率修正值、光强修正因子和温度修正因子，使用SPSS 专家建模功能，构建了输出功率预测模型。鉴于光强修正因子年周期变化规律的高度一致性，本文直接使用了历史光强修正因子作为预测值。

硅太阳电池阵输出功率预测值计算公式如下：

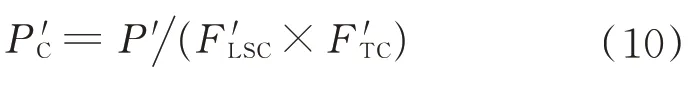
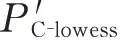
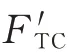
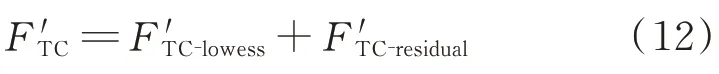
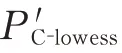
表1 长期预测模型Tab.1 Long-term prediction model

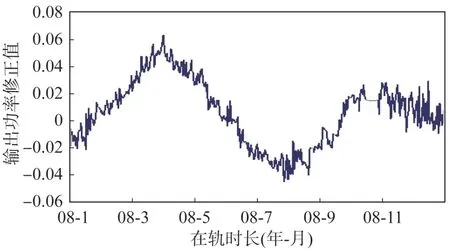
图9 联合修正输出功率的预测残差Fig.9 Prediction residual of the joint correction output power

图10 温度修正因子预测残差Fig.10 Prediction residual of the temperature correction factor

硅太阳电池阵在轨运行第9 年输出功率预测结果如图11 所示。图中，实线为预测值，散点为目前累积4 个月的硅太阳电池阵实际输出值。可见截至目前，预测效果与实际情况符合度较好。

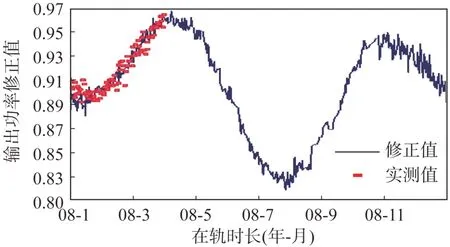
图11 输出功率预测曲线Fig.11 Prediction curve of the output power

模型误差和在轨遥测数据采集误差是产生预测误差的主要原因。硅太阳电池阵输出功率预测误差如图12 所示，可见实际预测误差保持在±25 W内，可以满足在轨管理使用需求。

图12 输出功率预测误差曲线Fig.12 Prediction error curve of the output power

4 结束语

本文以某地球同步卫星使用的BSR 硅太阳电池阵为研究对象，通过修正太阳电池阵输出功率计算结果，采用LOWESS 分析了其在全设计寿命期间的功率变化规律，并据此建立统计预测模型，用于硅太阳电池阵超寿运行期间的性能预测。后续我们将继续使用在轨实测数据对预测结果进行检验，同时针对单结砷化镓、三结砷化镓以及混合布片的地球同步卫星太阳电池阵在轨输出性能衰减规律展开研究。