基于主动阻尼控制的柔性基座振动抑制

周 政，邹怀武，储驻港，钟 楼，汤奇荣

（1.同济大学机械与能源工程学院 机器人技术与多体系统实验室，上海 201804；2.上海市空间飞行器机构重点实验室，上海 201108）

0 引言

随着空间在轨服务技术的发展，空间机械臂越来越多地被应用到航天器的维修、维护等任务之中。在空间站中，为了增加机械臂的操作空间，有时将其安装在移动基座上。移动基座先将机械臂移动至目标工作区域后锁紧，再由机械臂进行更加精细的操作。然而机械臂在运动过程中会不可避免地对基座产生反作用力，使得基座产生振动从而影响机械臂的操作精度。为了保证机械臂能够平稳操作，需要消除或者补偿对基座的反作用力以及力矩。对于柔性基座与机械臂系统的控制策略，共有3 类方法：第1 种方法，从反作用力入手，该方法通过规划1 条对基座产生反作用力最小的路径或者设计控制输入，从而有效地减少对基座的扰动，比如耦合图、反作用零空间法，但这类方法在受到外部扰动、基座产生振动的情况下不再适用。第2种方法，从机械臂控制入手，利用机械臂的运动来消除基座振动，这种方法存在一系列的缺点，比如控制方法的切换会带来力矩的突变，从而使得末端偏离稳态位置，对系统结构性能的要求也更高。第3 种方法，从基座的振动控制入手，通过设计系统输入，在实现机械臂轨迹跟踪的同时实现基座的振动控制，比如主动阻尼控制、惯性阻尼控制。惯性阻尼控制需要知道系统的频率特性，但不同的工作位置系统的频率特性不同。主动阻尼控制需要获取加速度反馈以及系统的惯性矩阵，但基座运动与机械臂运动可以得到有效解耦，系统可以保持良好的鲁棒性。

本文针对主动阻尼控制中系统惯性矩阵估计的问题，利用参数辨识的方法，以获取系统惯性矩阵较为准确的估计值，并在原始主动阻尼控制的基础上，添加基座位移补偿项以改进抑振效果。最后通过仿真验证，得到基座振动抑制以及机械臂关节空间轨迹跟踪结果。

1 柔性基座机械臂的动力学模型与参数辨识

1.1 柔性基座机械臂耦合系统建模

柔性基座机械臂系统简化模型如图1 所示，系统由1 个基座与2 关节机械臂组成。

图1 柔性基座机械臂系统Fig.1 Flexible base manipulator system

根据文献［11］，基座的柔性占主要因素，将机械臂视为刚性，柔性基座为弹簧-质量-阻尼系统，考虑平移位移，忽略旋转位移。图中，

C

为机械臂的质心，

m

为基座的质量，

K

为弹簧的刚度系数，

C

为阻尼系数。

基于这些假设，通过Lagrange 方程建立动力学模型如下：

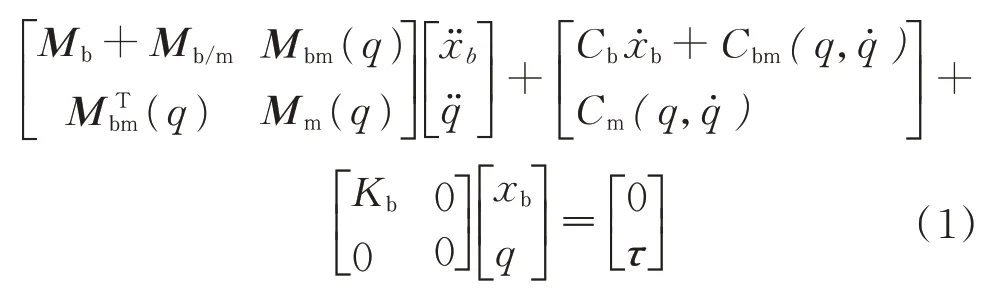
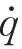
1.2 机械臂参数辨识

一般的机械臂动力学模型如下：

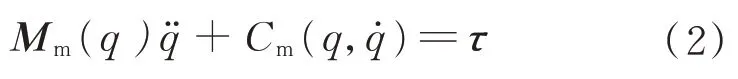
这类模型可以转化为机械臂惯性参数的线性函数，通过采集机械臂的运动数据，从而建立惯性参数的线性方程组，这样机械臂参数辨识的问题便转化为解线性方程组问题，即

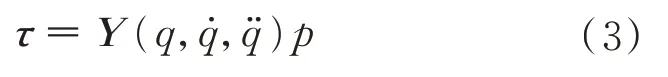
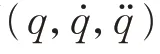
此外，参数辨识的精度与机械臂运动轨迹有关，机械臂按照预定轨迹运动时需要到达尽可能多的位姿和更好的参数辨识效果。有限项傅里叶级数轨迹常作为机械臂参数辨识的激励轨迹，采用如下公式作为各个关节的激励轨迹：

式中：

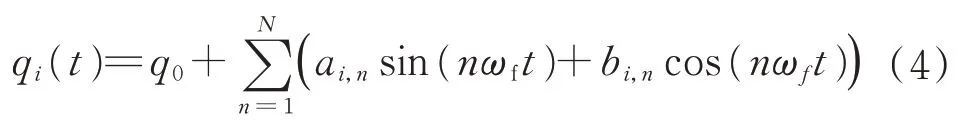
a

、

b

、

q

分别为傅里叶级数正弦项、余弦项系数、关节补偿。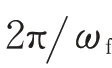

2 控制方案

2.1 机械臂与基座运动解耦

为了能够将机械臂的运动与基座运动解耦，从而分别对其控制，需要对机械臂的惯性矩阵进行估计。将估计值代入式（1）中的第2 行，得到

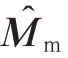
此估计值可由之前参数辨识所获得的结果得出，显示表达式为

式中：

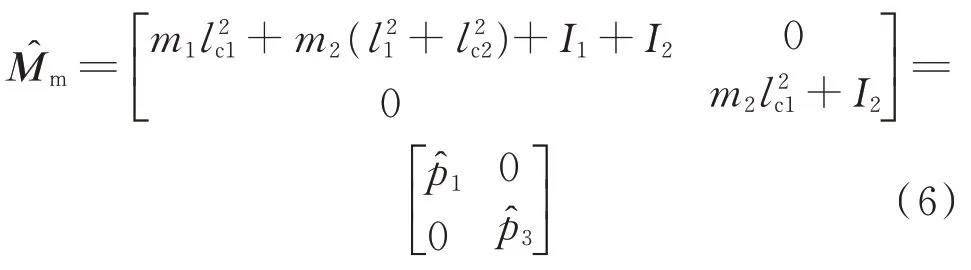
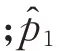
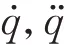
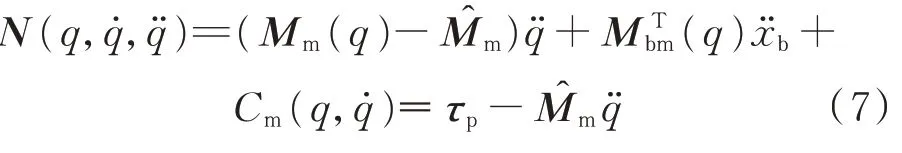
τ

为前一个采样时刻点的力矩数据，在采样频率很高的条件下，可以认为

τ

≈

τ

。

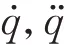
结合式（1）与式（8），将系统惯性矩阵求逆，改写系统动力学方程为

由式（9）可见，机械臂的运动与基座运动基本解耦，两者的运动同时由控制系统输入

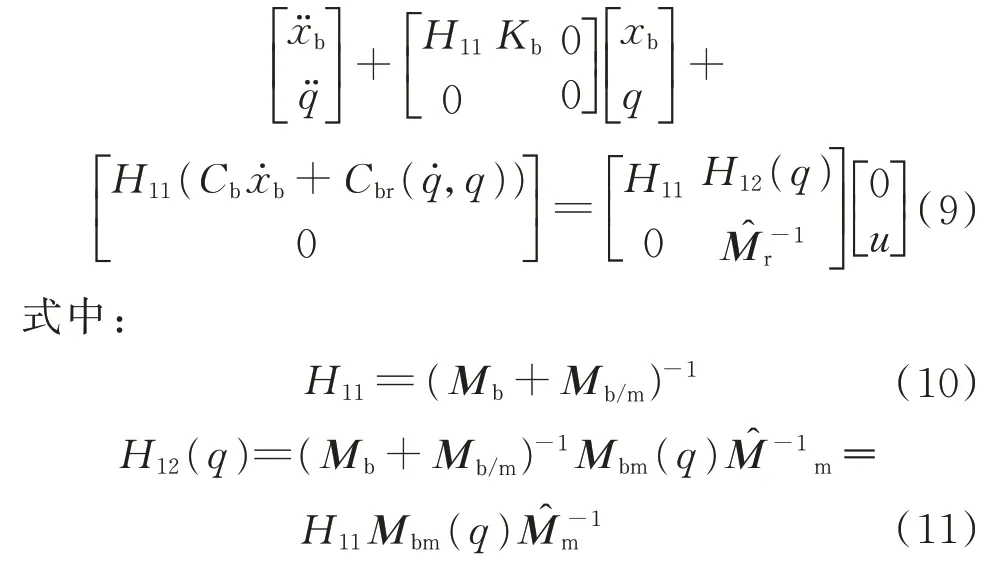
u

决定。

2.2 系统控制律设计

一个系统输入

u

需要同时控制2 个变量

x

与

q

，定义

u

由2 个部分组成：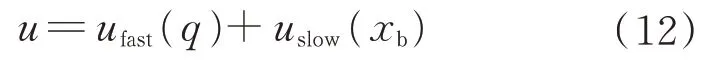

式中：

u

(

x

)主要作用于基座运动；

u

(

q

)主要作用于机械臂运动。

机械臂轨迹跟踪控制律的设计利用经典的计算力矩法的思想得出

相比基座运动的频率，机械臂的运动控制频率高得多，机械臂运动误差可以更快地得到收敛。此时

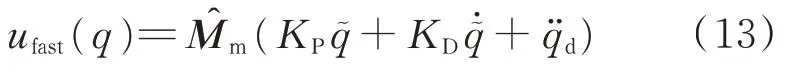
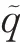
u

(

x

)可以当作一个常数，原始的主动阻尼控制原理中基座运动控制输入为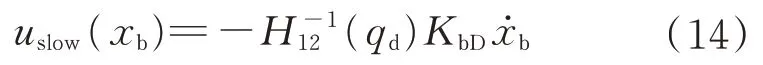

式中：

K

为阻尼控制系数。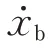

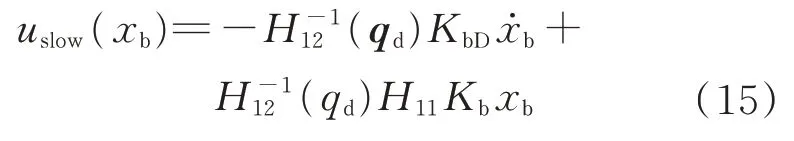
最后合并

u

(

q

)和

u

(

x

)，得到总控制律为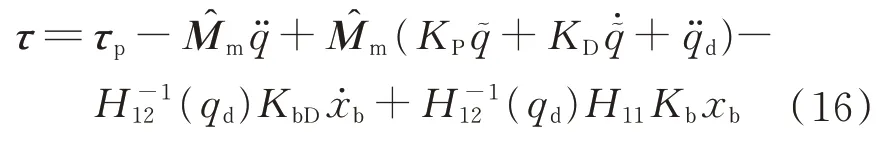

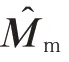
3 仿真试验及结果分析

考虑如图1 所示的机械臂系统，机械臂实际参数以及基座的等效模型参数见表1。在仿真过程中，机械臂的关节运动采用5 阶多项式，每个关节从0 rad 运动到2 rad，初始和结束时刻速度与加速度为0，运动时间为3 s，并在Simulink 中进行控制效果的验证。

表1 机械臂系统参数Tab.1 Parameters of the manipulator system

3.1 参数辨识结果

鉴于惯性参数集是非时变的，根据机械臂按照激励轨迹运动的数据，利用最小二乘法进行估计，辨识结果见表2。

表2 参数辨识结果Tab.2 Results of the parameter identification

此外，利用惯性参数的估计值进行力矩值计算，将各个关节的实际力矩与理论力矩进行对比，以验证辨识效果，对比结果如图2 所示。关节1 的平均力矩误差不超过10%，关节2 的平均力矩误差不超过2%，动力学参数辨识的结果可以用作后续惯性矩阵的估计。

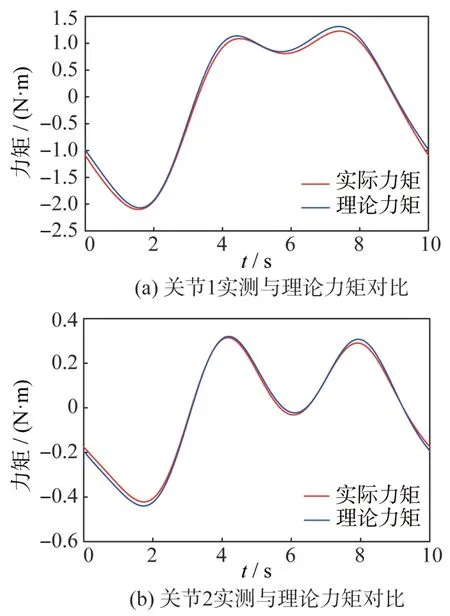
图2 参数辨识效果验证Fig.2 Verification of the parameter identification

3.2 基座抑振控制结果

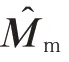
不同控制律下的基座的位移图像如图3 所示，可以清楚地看出机械臂关节运动给基座施加了一个用于抑制的阻尼力，根据参数辨识获取的惯性矩阵可以反映出系统的基本特性，以此设计的基座控制器抑振效果明显。此外添加基座位移补偿项后，虽然在机械臂运动过程中局部振幅变大，但在运动结束后的误差收敛速度明显优于改进前的控制律，同时稳态误差减小了不少。

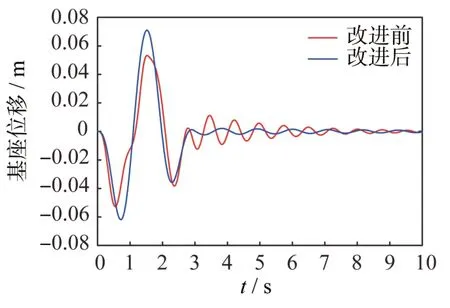
图3 改进前后控制律下基座位移响应Fig.3 Base displacement responses under the classical and improved control laws

机械臂关节轨迹跟踪误差的情况如图4 和图5所示。

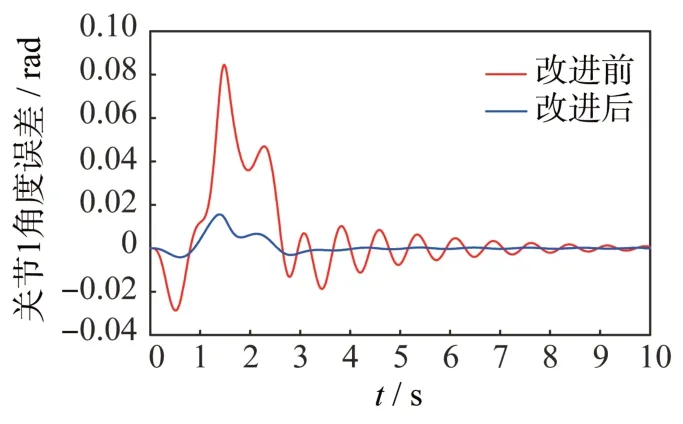
图4 不同控制律下关节1 角度误差对比Fig.4 Angle errors of Joint1 under the classical and improved control laws

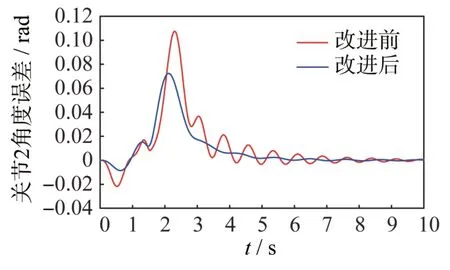
图5 不同控制律下关节2 角度误差对比Fig.5 Angle errors of Joint2 under the classical and improved control laws

实际上用于基座抑振的机械臂关节运动是在一个范围内左右摆动，以此产生相当于阻尼的效果，并且摆动的范围很小，基本不影响机械臂的正常操作任务。图中也给出了控制律改进前后的关节角度误差对比，可见添加了基座位移补偿项后获得了更高的轨迹跟踪性能，误差收敛得更快，在运动结束的3 s 左右就完成了基座抑振目标，而改进前需要更长的时间。

4 结束语

主动阻尼控制实质上是利用机械臂的左右摆动产生基座抑振的阻尼力，从而完成柔性基座的控制任务。这类方法控制律设计简单，并且能够保证关节空间轨迹跟踪精度。本文以2 自由度机械臂与弹簧-质量-阻尼的耦合模型为基础，通过在原始的主动阻尼控制律中加入基座位移补偿量，并利用参数辨识的方法估计惯性矩阵。验证结果表明，改进后的控制律能够以更快的速度达到误差收敛，达到了柔性基座振动抑制的目的，证明了方法的有效性，对于拓展到空间大型柔性结构系统有较好的参考价值。