海洋定位卫星性能分析

孙鸿强，张占月，赵焕洲，胡国林，张 辉，张 宽，谢 圆，卢 皓

（1.北京航天飞行控制中心，北京 100094；2.航天工程大学，北京 101416）

0 引言

人造卫星是重要的空间信息基础设施，其中的航天器编队飞行不仅突破了体积和质量的限制，而且提高了整体系统功能、结构灵活性和可替代性，近年来引起各国航天界极大的关注。编队卫星拥有不受基线限制、多星协同工作、控制灵活等特点，有着非常广阔的应用前景。常见的卫星定位功能通常由多个卫星协同工作完成，如美国的“白云”系列海洋监视卫星、我国的“北斗一号”定位系统。

以海洋定位卫星为例，可以满足对沿海、商业海域和重点海域的观察，重难点在于对目标的定位，但影响定位效果的因素众多，如受目标源位置影响、编队构型约束、卫星高度约束等。本文对三星定位的时差测量定位原理进行分析，将传统上评价卫星定位精度的水平精度因子（Horizontal Dilution of Precision，HDOP）与最小二乘迭代法相结合，对定位卫星的定位方程进行了解算，同时从定位精度和解算时长两个方面进行更直观的描述。在此基础上，分析了影响定位性能的若干条件给出了仿真验证结果，并以此对海洋定位卫星的参数设定提供建议。

1 三星定位编队定位计算模型

到达时间差（Time Difference of Arrival，TDOA）技术是采用比较广泛的技术。根据目标源的辐射信号到达卫星的时间，利用几何关系进行定位求解。在相同的测量误差条件下，时差越大，测量误差所占比例越小，误差造成的影响越小。对上述定位方法进行量化计算，联立方程得

式中：前两式为利用时差测量来确定2 张满足候选目标源位置的双曲面；

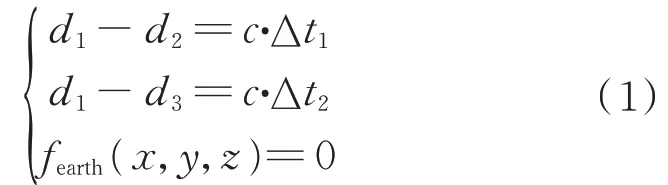
d

、

d

、

d

分别为3颗卫星到目标源的距离；

c

为电磁波传递速度；Δ

t

、Δ

t

为接受到目标源信号的时间差；

f

(

x

，

y

，

z

)为地球表面简化表达形式，地固坐标系下存在表示目标源位置3个未知量(

x

，

y

，

z

)。

2 三星定位误差分析模型

2.1 定位方程的最小二乘解算

对于式（1）中的

f

(

x

，

y

，

z

)，地固坐标系中的(

x

，

y

，

z

)转换到大地坐标系中的坐标(

L

，

B

，

H

)的转换方程为

式中：

N

为地球曲率半径；

H

为目标高度；

L

为目标经度；

B

为目标纬度；

e

为地球椭圆的偏心率。对于海洋定位卫星，

H

可取0，消去（

L

，

B

），可得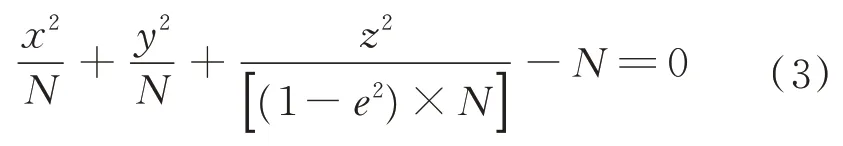

故三星时差定位方程改写为

式中：（

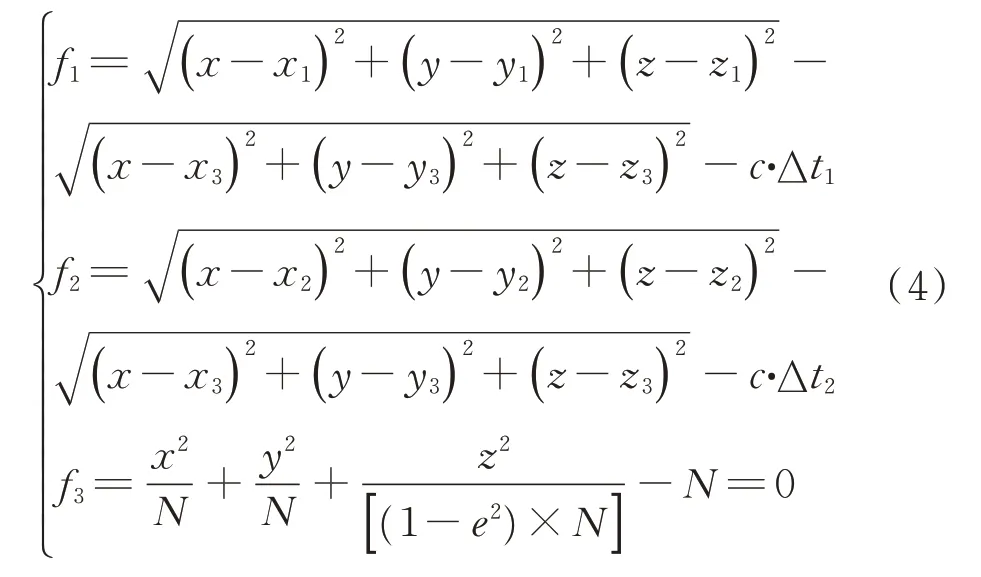
x

，

y

，

z

）为3 颗卫星在地固坐标系中的位置。

常用的解算方法有解析法、牛顿迭代法、最小二乘迭代法等。最小二乘迭代法具有平方收敛速度，可快速得到解算结果。

首先构建模函数

Q

(

X

)，将问题化为求解模函数最小值的问题：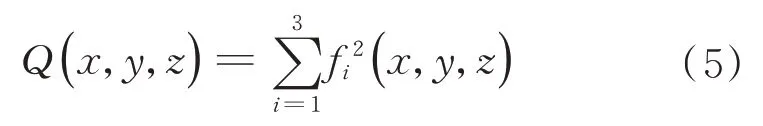

设

F

(

X

)=[

f

f

f

]，若

F

(

X

)可微，则模函数变化为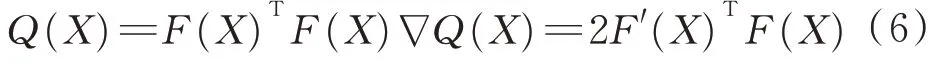

式中：

设

X

是

F

(

X

)=0 的一组近似根，将

F

(

X

)在

X

处泰勒展开略去高阶项：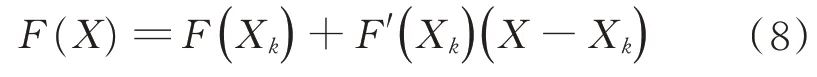

由最小二乘迭代可知，迭代误差Δ

X

可表征为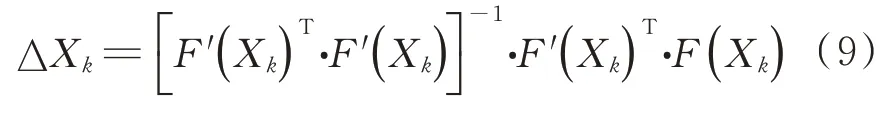

迭代步骤如下：

步骤1

取星下点为迭代初值

X

；

步骤2

将前一次求得的目标位置坐标

X

(

x

，

y

，

z

)代入定位方程，求出

F

(

X

)和

F′

(

X

)；

步骤3

将

X

(

x

，

y

，

z

)入迭代式，求出目标位置

X

(

x

，

y

，

z

)；

步骤4

以此类推，直到若干次迭代得

X

(

x

，

y

，

z

)与

X

(

x

，

y

，

z

)的距离小于某个无穷小的数

ε

。即设

当

D

<

ε

时迭代终止，求得极小点的近似值也就是目标位置的估计值。

采用上述解算方法将定位方程进行解算，如图1所示，初始概略位置选定在距离目标源1 310 km 处的位置，总定位误差随着迭代次数的增加迅速减小。

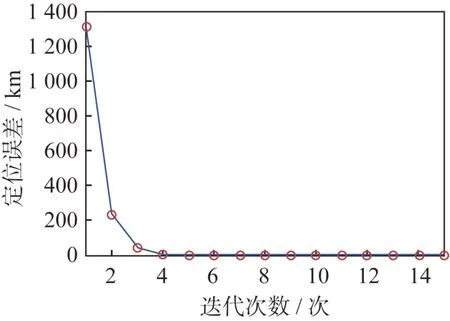
图1 迭代效果与定位误差Fig.1 Iteration effect and positioning error

2.2 定位方程的精度因子分析

由定位卫星的定位原理可知，在允许的范围内，如果目标源传递信号所到达不同卫星的时间差越大，定位效果越理想。如图2 左所示，理想情况下，以圆形为测量卫星测出目标源可能的位置（实线圈），以三角为测量卫星测出目标源可能的位置（虚线圈），两圈的交点即为目标源的位置（这里假设2 个交点中右侧的为目标源真实位置）。

而实际情况中误差是不可避免的，因此在测量时得到是圆环，2 个圆环的重叠处为目标源概略位置，如图2 中重叠的灰色区域。当2 颗卫星构型不理想时，如图2 右重叠的灰色区域面积过大，定位效果十分不理想。将式（4）中双曲面的表达式记为

图2 相对位置对定位精度的影响Fig.2 Effects of the relative position on the positioning accuracy

假设目标源在地固坐标系下的概略位置为

S

(

x

，

y

，

z

)，则将式（11）在

S

处展开，可得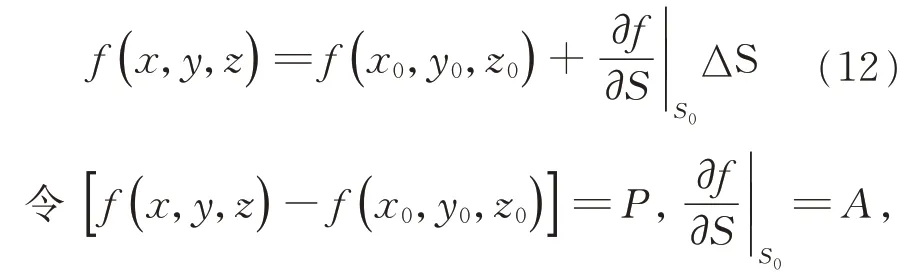

定位误差的协方差矩阵为

利用转换矩阵

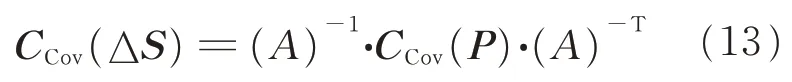
M

转化为建立在目标源当地坐标系协方差矩阵Δ

S

：

故目标源当地的误差协方差矩阵

C

(Δ

S

)可表示为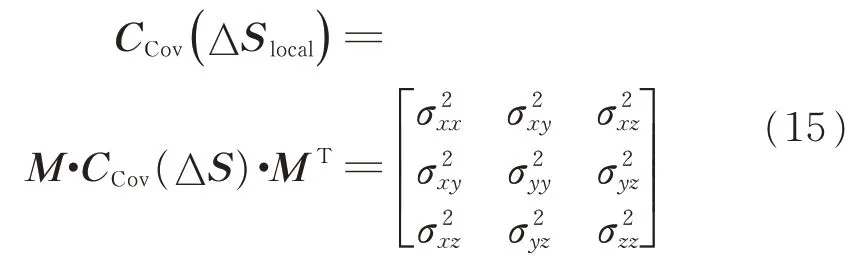

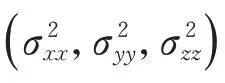
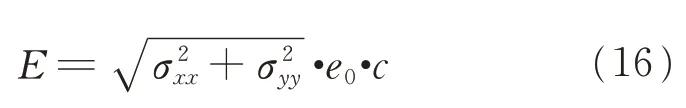
2.3 定位误差影响因素分析

2.3.1 目标源相对卫星位置的影响

为验证定位精度与目标源相对卫星几何位置之间的关系，对我国东部海域上的一块矩形区域进行覆盖仿真分析。选取的3 颗卫星位于2 个轨道上，将其真近点角进行了调整构成一个三角形。卫星场景分布如图3 所示。

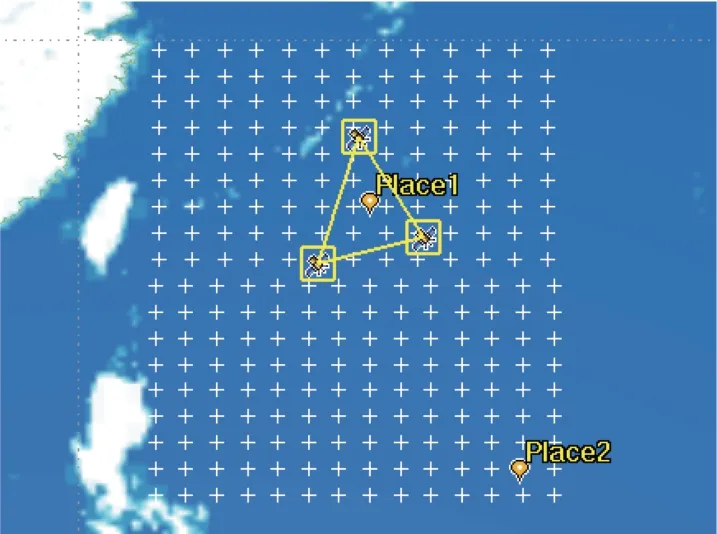
图3 卫星场景分布Fig.3 Satellite scene

定位卫星的星下区域内的HDOP 值如图4 所示。图中可见：在此三星构型的定位卫星中，当目标源在三星星下三角形之中时，HDOP 值较小；当目标源在三星星下三角形之外时，HDOP 值较高。

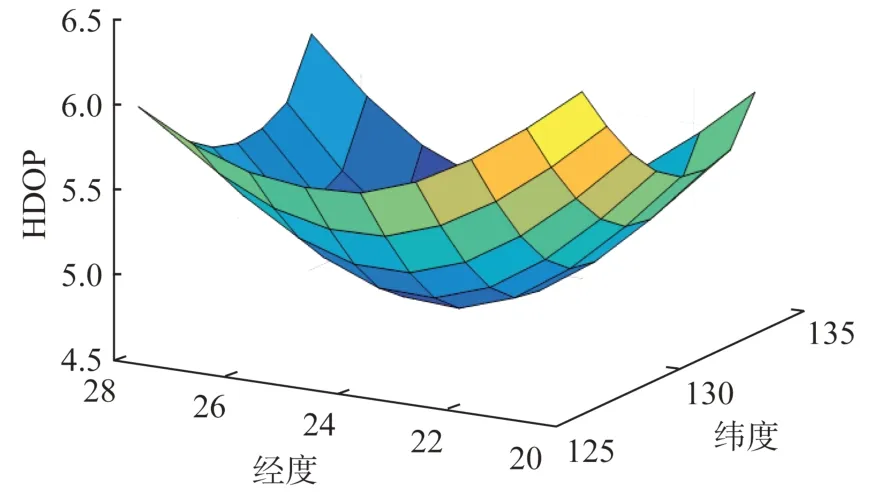
图4 HDOP 分布情况Fig.4 Distribution of HDOP

2 个不同目标源的误差变化情况如图5 所示。图中可见：位于星下点三角形内的点的距离误差很快就由初始误差迅速下降到零附近；而位于星下点三角形外的点距离误差下降缓慢，多次迭代内未达到理想误差精度。

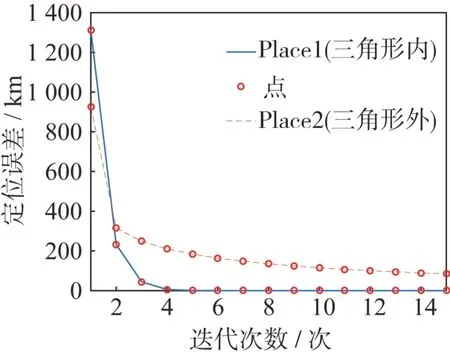
图5 不同目标源定位误差比较Fig.5 Comparison of positioning errors of different target sources

星下点和目标源的距离对迭代解算时间的影响如图6 所示。图中可见：随着目标源远离星下点，迭代解算次数逐渐增加，解算时间变长，性能变差。

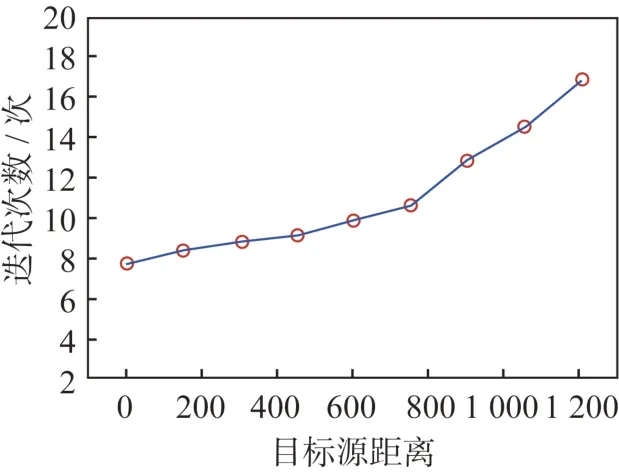
图6 目标源距离对迭代解算次数的影响Fig.6 Effect of the target distance on the iteration time

综合利用HDOP 和最小二乘迭代方法，对矩形区域内的点进行定位精度和迭代时长的分析，如图7所示。图中：绿色表示处于星下点三角形内的目标源，可以看出，其HDOP 值较低，意味着定位精度较高，且其定位解算时间较短，具有快速性和准确性；红色表示处于矩形边界的目标源，其HDOP 值较高，且解算迭代时间较长；此外，还存在一部分处于星下三角形周围的点（蓝色），其定位精度也较高，但是迭代其解算时间相对较长，定位效果不如星下三角形内的点。因此，从定位精度和解算时间上综合考虑，目标源位于星下三角形内时，定位性能更强。

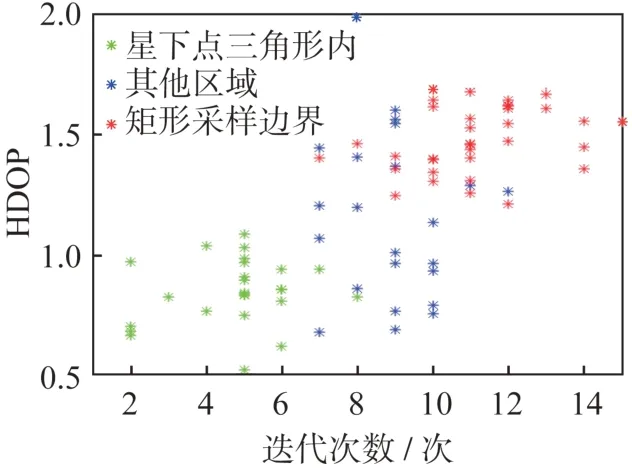
图7 不同目标源定位精度和迭代解算次数比较Fig.7 Positioning accuracy and iteration times of different target sources

2.3.2 卫星高度影响

取上述卫星场景，保证3 颗定位卫星的星下点构型不变化，只改变其高度，分析卫星高度的影响。卫星场景如图8 所示。

图8 卫星场景图Fig.8 Satellite scene

卫星高度和星下点三角形区域内HDOP 的变化关系如图9 所示。图中：下方虚线表示在对应高度下星下点三角形区域中的最小HDOP 的值；上方虚线表示在对应高度下该区域中的最大HDOP 的值；实曲线表示该区域中的平均HDOP 的值。图中可见：在一定范围内，随着卫星高度越高，其对于地面上同一目标源的HDOP 越大；而卫星高度越低，对于地面上同一目标源的HDOP 越小。

图9 卫星高度变化对HDOP 的影响Fig.9 Effect of the satellite altitude change on the HDOP

2 组不同高度定位卫星的基于定位方程的迭代次数与距离误差之间的关系如图10 所示。图中可见，在解算过程中，尽管经过若干次迭代，定位误差逐渐降低，达到了理想的精度，但是在解算过程中，该场景下当卫星轨道半长轴为6 800 km 时，定位解算的迭代次数较多、时间较长，相对而言该场景下当卫星轨道半长轴为7 500 km 时，定位解算的迭代次数较少、时间较短。这与HDOP 变化相反，从迭代解算时间上比较，7 500 km 更优。

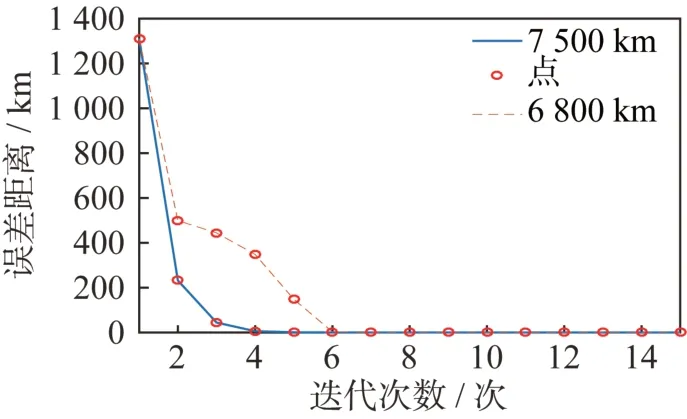
图10 多次迭代后不同高度定位误差比较Fig.10 Comparison of the position error on different altitude

而对不同高度编队卫星而言，其迭代解算时间亦不同，将轨道半长轴范围设定在6 700～8 500 km，与之对应的迭代解算次数如图11 所示。可以看出，随着编队卫星高度的增加，迭代时间逐渐减小，在轨道半长轴为7 000 km 时达到最小，而后迭代时间随着高度增加逐渐增大。由此，从迭代解算时间分析，并不是轨道高度越低越好。

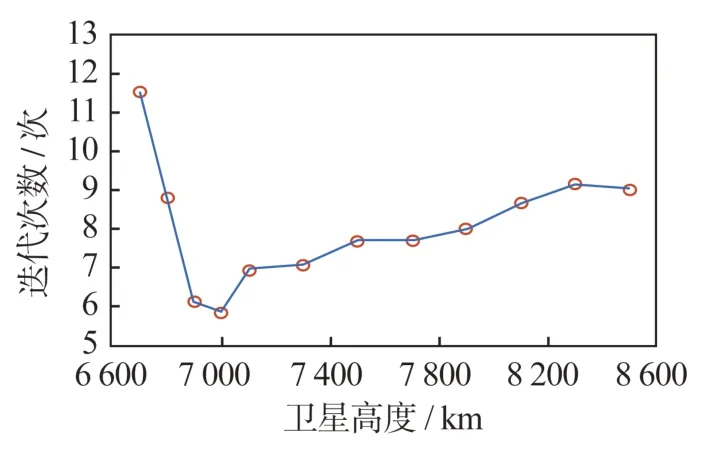
图11 不同高度对迭代次数的影响Fig.11 Effect of the satellite altitude on the iteration time

利用HDOP 和最小二乘迭代方法对不同高度的卫星进行定位精度和迭代时长的分析，如图12 所示。图中可见：在卫星高度很低时，虽然HDOP 值越小，但是其迭代解算时间较长；随着卫星轨道高度逐渐升高，迭代解算时间呈现先减少后增加的趋势。因此，从定位精度和解算时间上综合考虑，定位卫星的高度并不是越低越好，应该在综合考虑对地观察面积、定位精度和迭代解算效率，选择适用于不同任务目标的卫星参数。

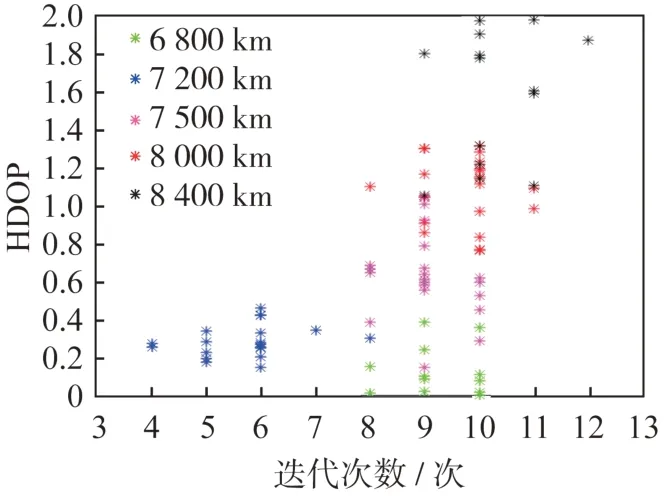
图12 不同高度卫星定位精度和迭代解算次数的比较Fig.12 Comparison of positioning accuracy and iteration times of different altitude

2.3.3 几何构型的影响

在分析星下点三角形底边高的影响时，选取对应构型对该区域内的平均HDOP 和定位误差进行比较分析。保持星下点三角形左侧的边不变，调整三角形右下方顶点的位置，使得三角形左侧底边上的高逐渐变大，卫星场景如图13 所示。

图13 改变星下点三角形左侧底边的高Fig.13 Change of the left base height of the triangle

星下点三角形左侧底边的高和该区域内HDOP 的变化关系如图14 所示。图中：上方虚线表示在对应高下星下点三角形区域中的最大HDOP的值；下方虚线表示在对应高下该区域中的最小HDOP 的值；实曲线表示该区域中的平均HDOP 的值。图中可见，在一定范围内，随着星下点三角形左侧底边上的高变长，其对于地面上同一目标源区域的HDOP 越小，反之越大。

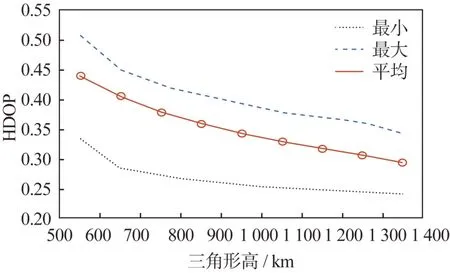
图14 三角形高的变化对HDOP 的影响Fig.14 Effect of the triangle height on the HDOP

2 组星下点三角形左侧底边高不相等的定位卫星的距离误差如图15 所示。对两者的定位精度进行比较，由图可知，在定位精度方面，星下点底边高较长的卫星的定位精度较高。在实际定位过程中，卫星之间的基线不宜过长，需要在保证编队可控的情况下进行基线的最优化。

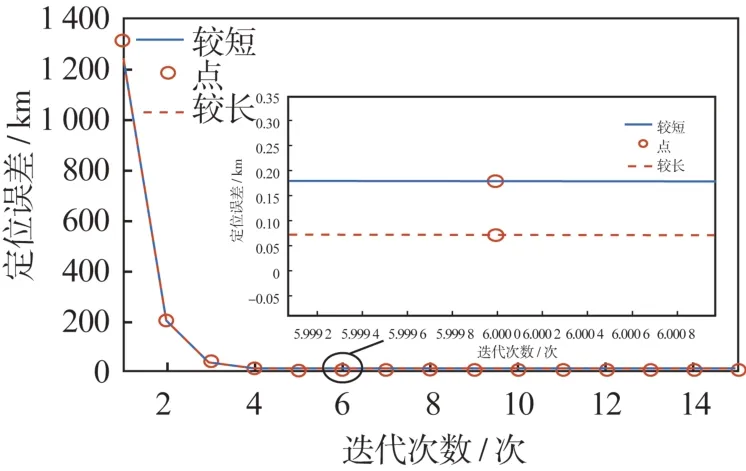
图15 多次迭代后定位误差比较Fig.15 Comparison of positioning errors after several iterations

星下点三角形左侧底边高的变化对迭代解算时间的影响如图16 所示。图中可见，在其有限的变化范围内，平均迭代次数未发生明显改变，星下点三角形高的变化不是影响迭代结算时间的主要因素。

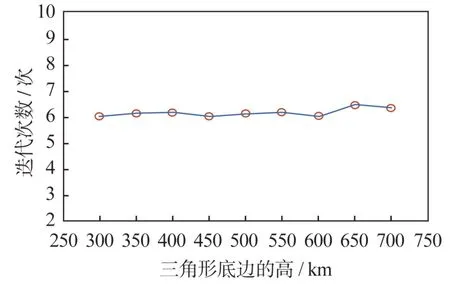
图16 底边的高对解算时长的影响Fig.16 Effect of the triangle height on the iteration time

利用HDOP 和最小二乘迭代方法对所构成不同三角形底边高进行定位精度和迭代时长的分析，如图17 所示。图中可见：在一定范围内，三角形底边高越长，其HDOP 值越小；但从迭代解算时间来看，在一定范围内其迭代时间变化不大，这是由于卫星编队的星间距离不宜过长从而限制底边高的最大值所导致的。因此，从定位精度和解算时间上综合考虑，在工作允许的范围内，定位卫星星下三角形底边的高越长，定位性能更强。

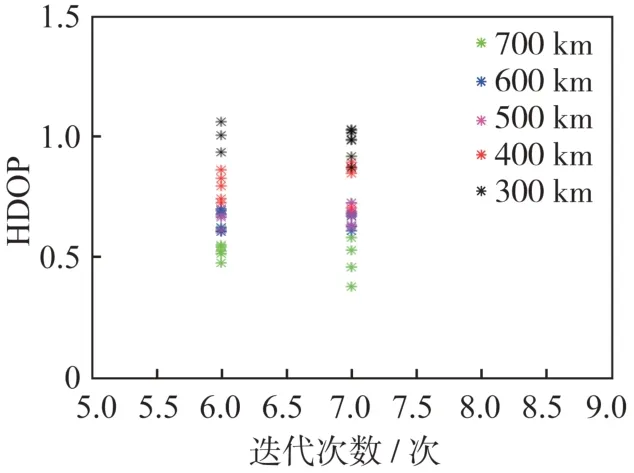
图17 不同底边高的定位精度和解算迭代次数的比较Fig.17 Positioning accuracy and iteration times with different triangle heights

综上分析，在此三星构型的定位卫星中，当目标源在三星星下点构成的三角形之中时，定位精度较高、解算时间较短，卫星的性能比较理想；当目标源在三星星下点构成的三角形之外时，定位精度较差、解算时间较长，卫星定位性能不够理想。同时，在一定范围内，卫星高度越高，对地面上同一目标源的定位精度越差，但迭代解算时间随着高度的增加呈现先减少后增加的趋势，因此，a 卫星性能和卫星高度呈非线性的关系，应综合考虑对地观察面积、定位精度和迭代解算效率，选择适用于不同任务目标的卫星参数。此外，在构建三星位置构型时需要注意，在允许范围内，随着星下点三角形一边的高不断变大，对区域的定位精度逐渐变高，解算时间改变较少，综合卫星性能亦逐渐增强。

3 结束语

本文在时差测量定位的基础上分析了三星定位误差的产生，通过定位方程的求解对定位精度和迭代次数进行了分析，在此基础上，以水平方向衰减因子HDOP 与迭代解算时间作为指标，对三星定位卫星进行定位性能评价。验证了在进行卫星轨道设计时，需要尽可能地将目标源包括在星下点三角形之中，定位卫星的高度在允许范围内适当降低，星下点三角形底边上的高在允许范围内尽可能大。此外，在应对突发情况需要对航天器进行机动操作时，为保证机动之后的工作效率，可以利用本文作为参考，设计航天器的机动转移轨道，这样才能保证海洋定位卫星的定位精度。