大月池开口钻井船阻力与流场特性
何进辉,张修远,张海彬,羊 卫,郭春雨
(1.上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室,上海 200240;2.中国船舶及海洋工程设计研究院,上海 200011;3.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001)
0 引 言
钻井船是海洋油气资源勘采的重要装备,在当今世界对海洋资源开发利用需求快速增长的背景下,深海钻井船的设计建造数量大幅增加。钻井船月池结构底部与海水相连,其内部流体流动复杂,会产生分离流和波浪破碎等强非线性现象,使船舶航行阻力显著增加。近些年,ERIK等[1]对二维月池结构的流场进行数值模拟,并分析流场特性,同时对以二维月池结构阻力特性向三维月池结构阻力预报进行可行性研究。孙采微[2]应用数值计算方法对两种带有月池的钻井船阻力进行预报研究,并形成针对月池结构的阻力性能分析方法和计算流程。李志雨等[3]使用CFD方法对船舶月池流场及其所带来的附加阻力进行研究。
在过去的研究中,虽然针对带有月池船舶的静水航行阻力得到了一些结论,但是对于带有月池船舶的CFD计算方法还没有深入研究。本文应用国际标模KVLCC2进行钻井船阻力数值预报中相应网格与设置验证,证明本计算中网格与数值方法的正确性,并对带有大月池开口的钻井船的阻力与月池内流场特性进行计算研究。
1 模拟对象及工况
采用中国船舶及海洋工程设计研究院设计的某型带有月池结构的超深水钻井船为研究对象。为验证计算方法的准确性,对国际标模KVLCC2进行数值模拟计算,与试验结果进行对比验证。KVLCC2和钻井船模型分别如图1和图2所示,模型的详细参数与工况如表1所示。

图1 KVLCC2船舶模型
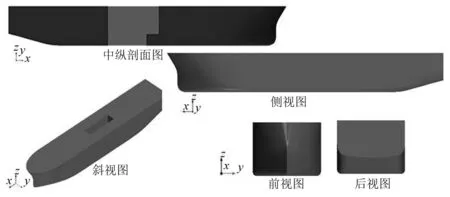
图2 钻井船模型
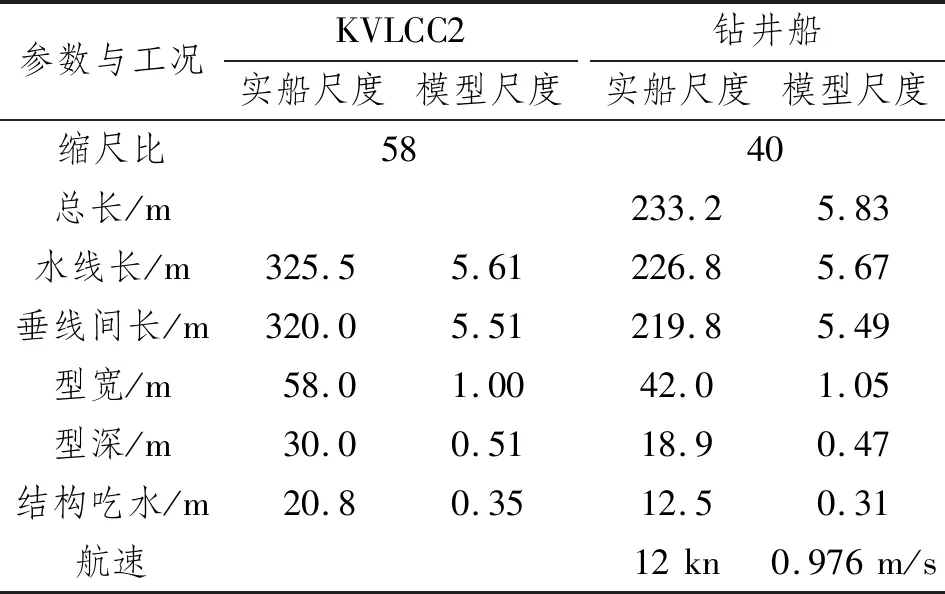
表1 KVLCC2及钻井船模型主要参数与计算工况
2 数值模型及网格划分
2.1 数值模型
2.1.1 控制方程
不可压缩牛顿流体运动满足的连续性方程和动量守恒方程[4-5]为
(1)
(2)
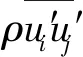
2.1.2 离散方法和空间离散格式
使用STAR-CCM+商用软件,调用其流体力学数值计算功能对船舶航行状态下的流场状态进行数值模拟计算。其中,运算中的控制方程采用基于压力的耦合算法求解,采用二阶迎风格式进行空间离散,采用二阶中心差分格式进行耗散项的离散。
2.1.3 自由液面的处理
HIRT等[6]开创性地提出流体体积(Volume of Fluid,VOF)方法。VOF方法并不计算跟踪自由液面上流体质点的运动,而是通过计算网格单元中流体占有的空间比例确定自由液面。该方法可较好地捕捉复杂流体自由液面现象,如翻转、吞并、飞溅等,同时在计算时占用计算机内存少,易实现三维几何空间的自由液面计算。在该方法中,假定大计算域的体积为V,内有2种互不相容的流体物质,其中:第一种流体所在区域的体积为V1;第二种流体所在区域的体积为V2。定义函数:
(3)
对于由不相容的流体组成的流场,α满足:

(4)
式中:U=(u,v,w)为计算域内流场的速度场,定义VOF函数C为α在网格单元上的体积除以单元体积,即
(5)
且C满足:
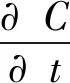
(6)
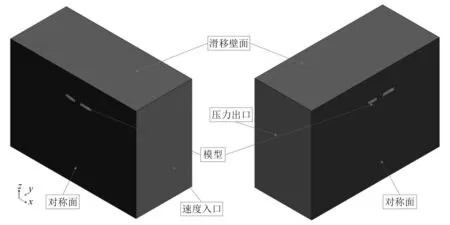
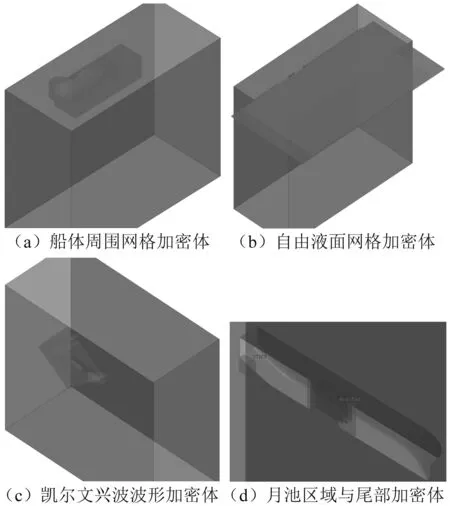
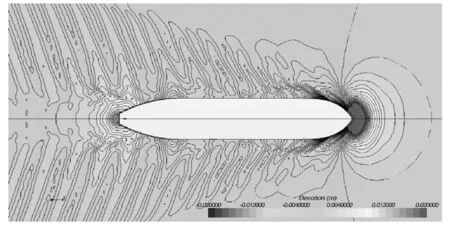
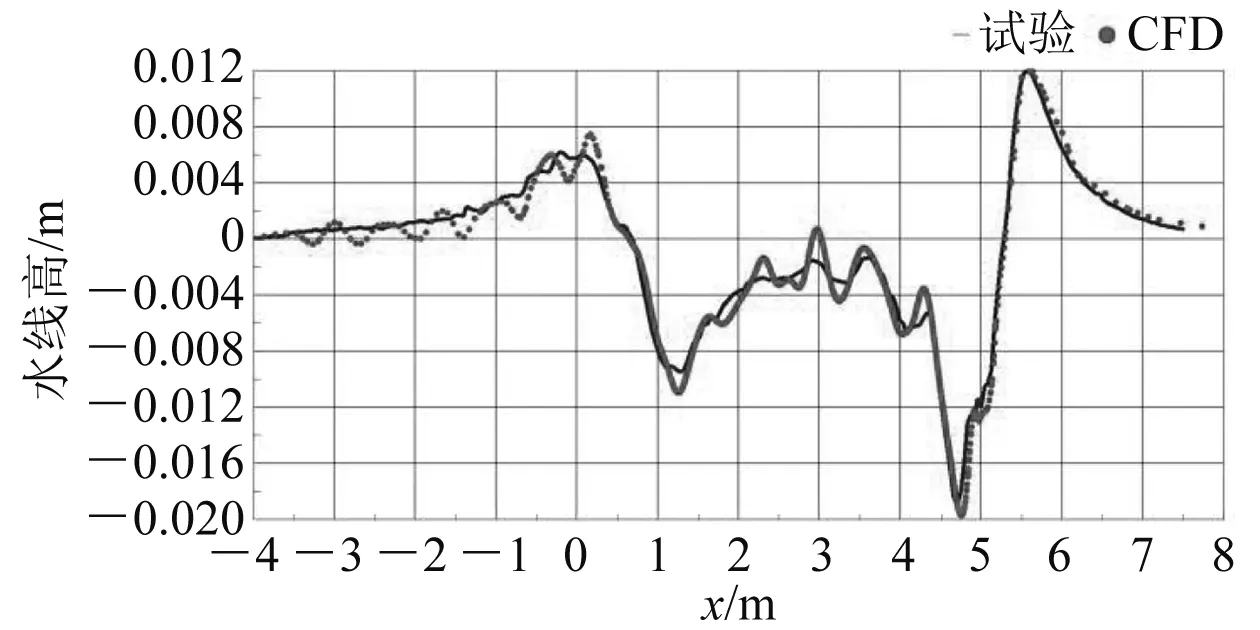
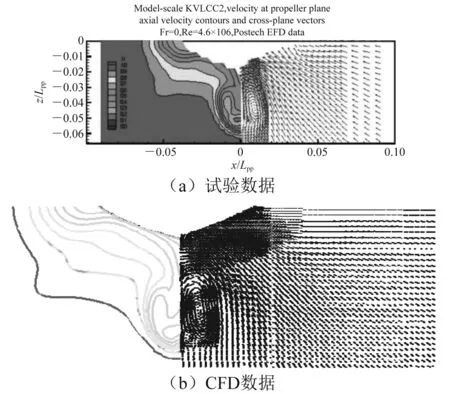
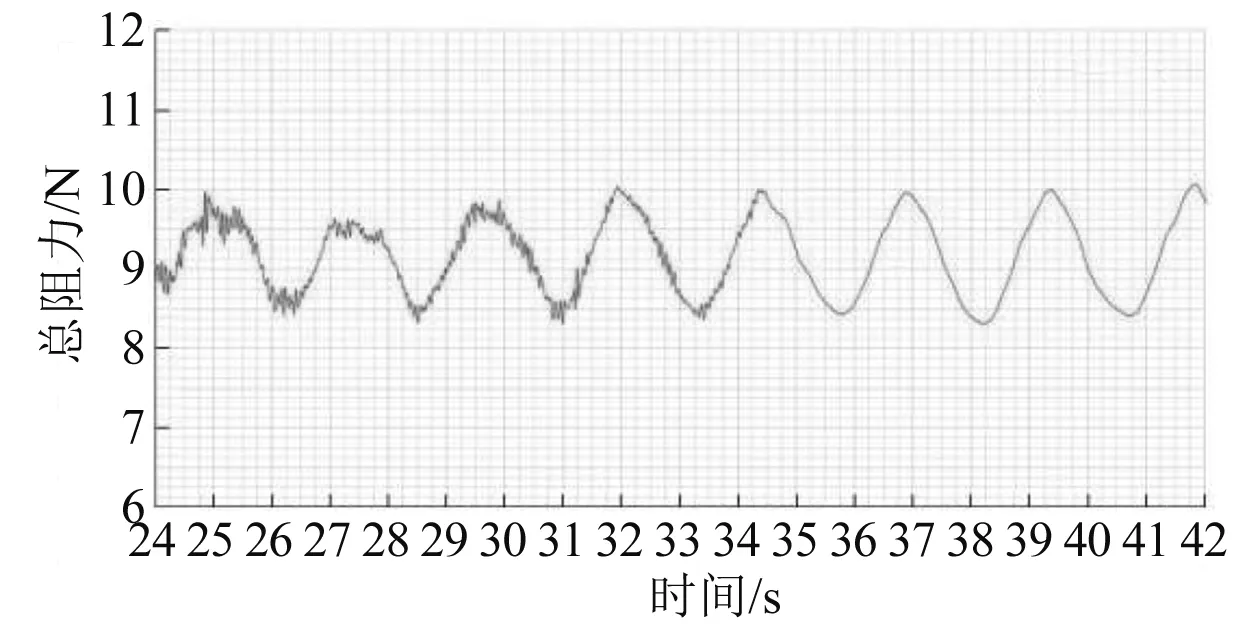
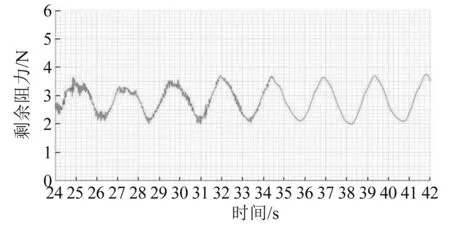
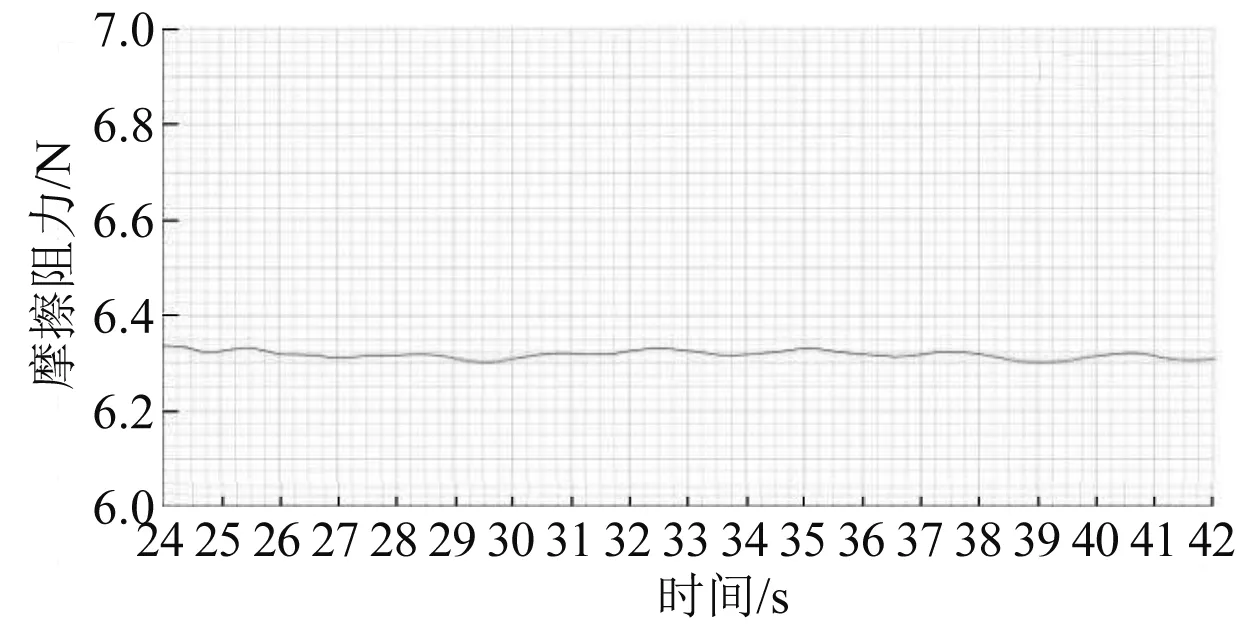
当C=1时,网格充满第一种流体I;当C=0时,网格不含第一种流体;当0 2.1.4 数值消波 在计算设置中,应对计算域的边界进行设定与消波处理,防止自由液面兴波在边界反射而对计算结果造成影响。使用文献[6]方法,在边界加入一个垂向阻尼,削弱波的垂向运动,以达到消波的目的。阻尼方程为 (7) 其中: (8) 式(7)和式(8)中:Sz,d为添加的动量源项;f1、f2和nd为消波参数;w为垂向速度分量;xsd为消波起点;xed为消波终点或边界。 在大月池开口钻井船阻力性能数值研究中流场与船体模型都具有对称性,即船体与流场都相对于中纵剖面对称,因此在计算模型对象上选择船体中纵剖面的一侧,来流方向的计算域范围取-2.0Lpp≤x≤3.0Lpp,展向方向的计算域范围取0Lpp≤y≤2.0Lpp,垂向方向的计算域范围取-2.5Lpp≤z≤1.0Lpp,其中Lpp为模型的垂线间长。图3为计算域示例。 图3 计算域示例 研究中用到的计算网格由STAR-CCM+软件生成。使用该软件中的网格生成模块对模型表面进行处理,进行面网格重构,使模型表面三角化,之后以三角形面网格为基础,以一定增长率在计算域中生成边界层,最后形成切割体网格,形成体网格。 通过定义体积控制区域,STAR-CCM+可在不同位置以不同形状对网格进行加密,图4为钻井船不同区域的网格加密示例,其中:图4(a)为船体周围网格加密体,加密体由最近、近、中和远等4个加密体组成;图4(b)为针对流场自由液面的网格加密体,加密体由粗、中、细和最细等4个加密体组成;图4(c)为凯尔文兴波波形周围网格加密体,加密体由远场和近场2个加密体组成;图4(d)为月池区域和船尾区域周围网格加密体。 图4 钻井船不同区域网格加密体 钻井船网格与数值验证采用KVLCC2的试验值,计算域构建与网格划分方法保持一致。由阻力与流场计算验证结果可知,KVLCC2数值计算与试验阻力的相对误差为0.4%,达到工程精度要求。自由液面波形分布如图5所示,船身波形切面如图6所示。计算结果显示计算网格的凯尔文波形加密设置保证了船舶自由液面波形的高精度捕捉,船身波形切面数值与试验的比较验证了自由液面的计算精度。 图5 波形分布 图6 波形切面数值与试验值对比 船舶标称伴流场的试验与数值对比[4]如图7所示。计算结果显示,KVLCC2的钩状伴流特性与舭涡和毂帽涡旋涡特性均得到了较好的模拟和预报。 图7 标称伴流场试验与数值对比图 将KVLCC2的阻力、自由液面波形和船尾伴流场数值与试验值进行对比,验证钻井船网格加密形式、划分策略和数值模型选择的正确性。 进行无月池钻井船阻力数值计算,将无月池钻井船的摩擦阻力数值计算结果与1957年国际船模实验池会议实船-船模换算公式(简称“ITTC 1957公式”)的计算结果进行对比。精度为粗网格1.830%、中网格1.795%、细网格1.775%。在计算中3套网格均有较好的计算精度,且随着网格的细化精度增高而增高。综合考虑计算精度与计算效率,中网格可达到计算要求。对于大月池开口钻井船的阻力数值计算,由于大开口月池的存在,月池内的自由液面会发生周期性的波面变化,受自由液面直接影响的剩余阻力会发生周期性波动,总阻力也会随时间发生周期性变化。船舶总阻力、剩余阻力和摩擦阻力曲线如图8~图10所示。瞬态计算格式下的船舶总阻力、剩余阻力均随着月池液面的波动产生周期性的波动;船体摩擦阻力基本不受月池液面波动的影响,不发生周期性波动。 图8 大月池开口钻井船总阻力曲线(瞬态) 图9 大月池开口钻井船剩余阻力曲线(瞬态) 图10 大月池开口钻井船摩擦阻力曲线(瞬态) 自由液面波形瞬态与稳态计算结果对比如图11所示。由图11可知,瞬态和稳态计算模式均对船舶自由液面波形进行了较完整的捕捉,但是稳态的自由液面的整洁程度较瞬态计算结果差。稳态计算格式基本捕捉到了整体的波形特征。瞬态计算格式的波形比稳态更好。 注:上侧为瞬态;下侧为稳态图11 瞬态与稳态自由液面兴波对比 图12为启动初始阶段月池内自由液面的瞬态波动特性计算结果,瞬态计算格式可更好地捕捉自由液面波动特性。月池内自由液面会产生静止状态下受启动速度影响与月池壁面发生碰撞,返回后与另一面的壁面碰撞的现象。稳态的流线计算结果对船体月池内旋涡等月池内流场进行捕捉,但是月池上端与空气相互作用的旋涡流场和旋涡涡结构的范围则没有瞬态计算格式捕捉的精细,如图13所示。瞬态计算格式和稳态计算格式分别对月池后端区域的边界层进行了较好的捕捉,瞬态计算格式对月池内部的速度分布较稳态计算格式捕捉更精细。 注:0~0.95 s,间隔为0.05 s图12 启动阶段月池自由液面瞬态波动特性 图13 月池内流线分布 大月池开口钻井船的涡结构瞬态计算结果如图14所示。由图14可知,瞬态涡结构计算结果对船体舭涡、尾部流动分离、大月池开口的月池泄出涡均进行了较好的捕捉,图14中椭圆虚线框出的区域为大月池开口的泄出涡区域,可看到泄出的涡结构,下侧的矩形虚线框为月池泄出的涡结构随着水流作用向下游传递的过程,上侧的矩形虚线框为舭部区域产生的舭涡结果。 图14 瞬态计算格式下的涡结构 大月池开口钻井船的涡结构稳态计算结果如图15所示。由图15可知,稳态计算格式并不能把船舶舭涡、月池泄出涡和涡结构随着时间的传递与演变进行很好的捕捉与模拟。在稳态计算格式下的数值计算中,船尾舭涡和流动分离与舭涡的传递没有预报的范围大,且存在涡结构混乱因素、涡结构图像不整洁。另外,对于大月池开口处泄出的涡结构与涡结构的传递过程,稳态计算格式在求解本身与实际求解结果上都显示了较差的求解能力。 图15 稳态计算格式下的涡结构 因此,对于大月池开口钻井船涡结构,特别是在涡结构的产生、泄出、传递过程的数值模拟中,瞬态计算格式强于稳态计算格式。图16为通过计算格式对比后应用瞬态计算进一步展示船舶涡结构数值计算结果图。瞬态计算结果可更好地捕捉到自由液面波动涡结构、船体舭涡、月池端部泄出涡,且泄出涡沿着船体的传递也得到了较好的捕捉。 图16 船舶涡结构数值计算结果图 基于CFD的阻力数值预报方法,形成适用于大月池开口钻井船阻力及流场数值预报的方法和流程。相关结论如下: (1)大月池开口钻井船的自由液面兴波与月池中波面的波形产生、传播与演化的过程本身是一个瞬态过程。瞬态计算格式在物理现象的发展上与实际情况吻合,在数值的求解过程中也符合VOF算法要求。瞬态计算格式比稳态计算格式更适合于大月池开口钻井船阻力数值预报。 (2)对于具有自由液面的大月池开口瞬态CFD计算问题,考虑到在计算初始阶段会出现较明显的堆水现象以及月池内部的剧烈晃荡,一般在最开始的求解时刻选择调低时间步长。 (3)大月池开口钻井船模型阻力数值预报流程主要包括数值预报中模型预处理、体网格划分、计算加密区构造与设置、计算模型设定、初始条件设定、边界条件设定、自由液面与消波模型设置、求解器参数设置、时间步长选取、力与流场监测等内容。2.2 计算域建立与体网格划分
3 计算结果与分析
3.1 基于标模KVLCC2的钻井船网格与数值设置验证
3.2 大月池开口钻井船模型阻力数值预报
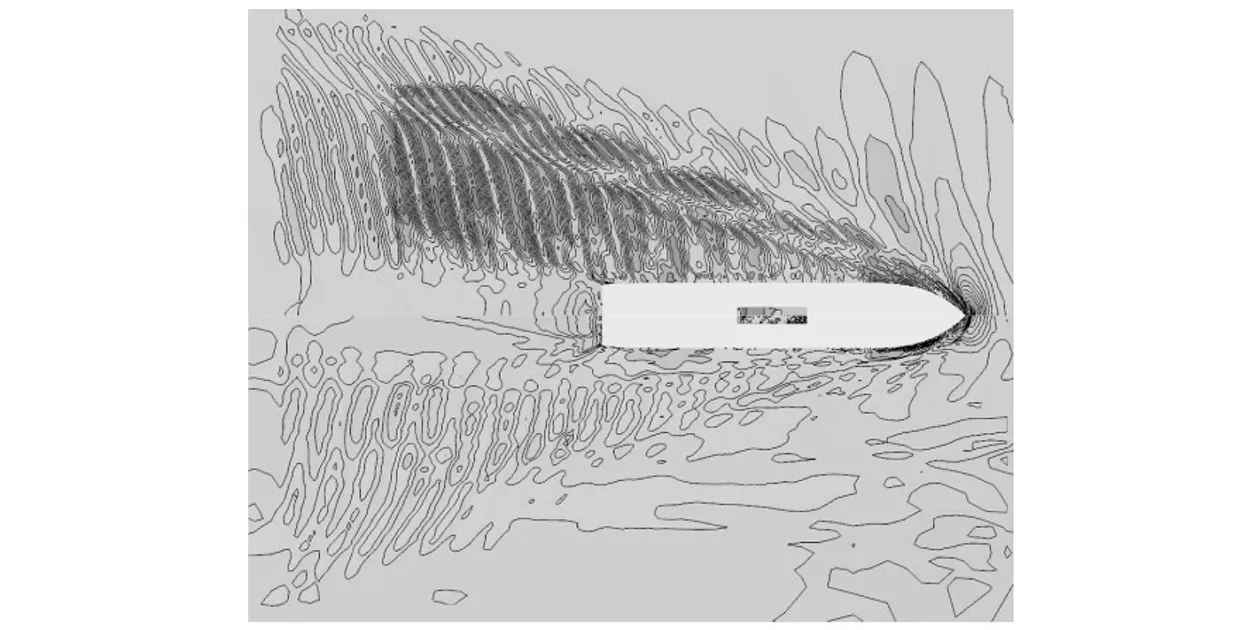
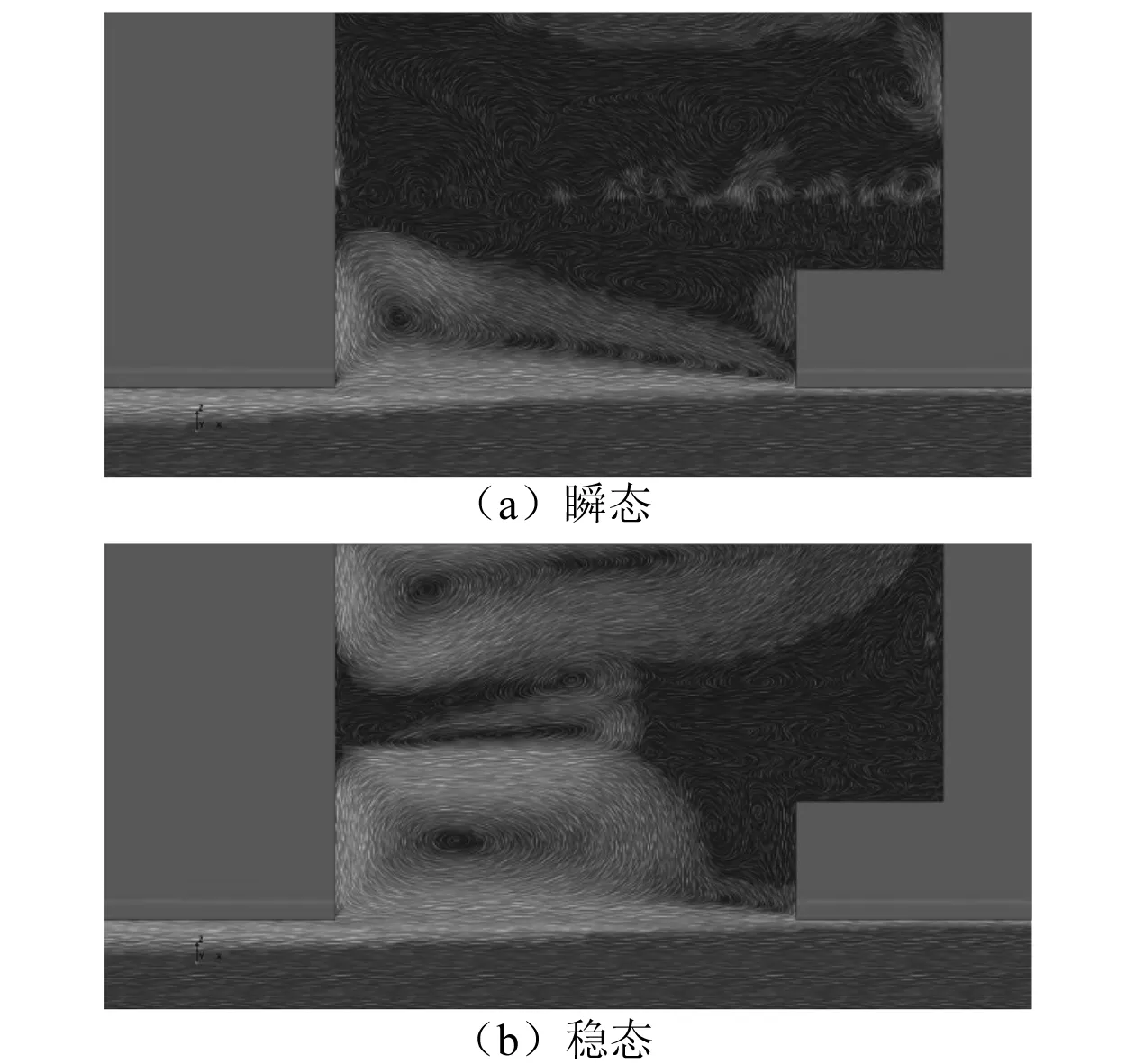
3.3 大月池开口钻井船自由液面波形与月池内部流动分布

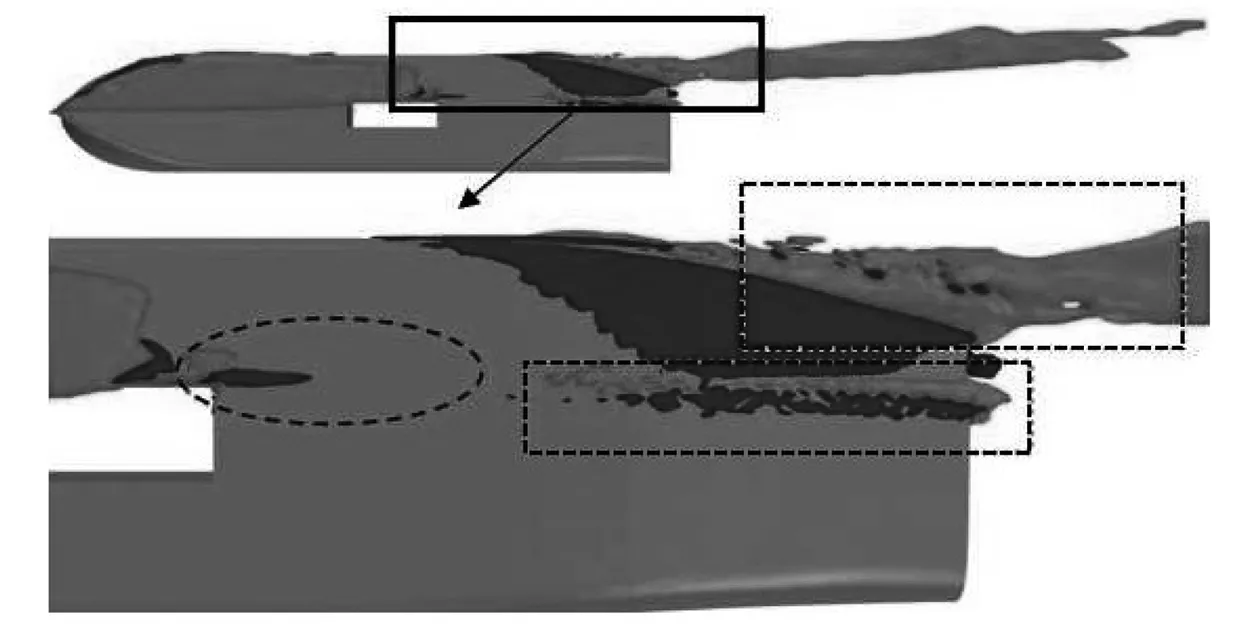
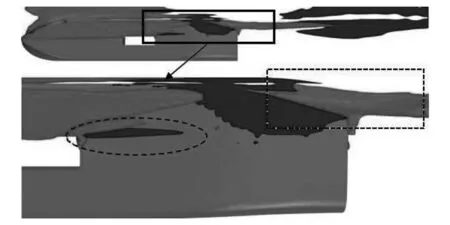
3.4 大月池开口钻井船涡结构分布

4 结 论

