基于AR 模型的人均国民总收入预测

蔡 新

（贵州财经大学，贵阳 550000）

0 引言

2000 年，我国人均国民总收入只有940 美元，属于世界银行根据人均国民总收入划分的中等偏下收入国家行列；2010年，我国人均国民总收入达到4 340 美元，首次达到中等偏上收入国家标准；2019 年，我国人均国民总收入上升至10 410 美元，高于中等偏上收入国家9 074 美元的平均水平。现阶段，人均国民总收入继续保持上升，已经取得全面建成小康社会的历史性成就，已经基本实现全面建成小康社会的目标。基于我国目前的经济情况，本文将对1978 年至2019 年的人均国民总收入数据进行分析，并预测2020 年及2021 年人均国民总收入水平。

1 模型介绍

1.1 自回归模型（AR（p））

自回归模型是最简单的ARMA 模型，它是仅用时间序列Yt不同滞后项作为解释变量的模型。模型形式如下：

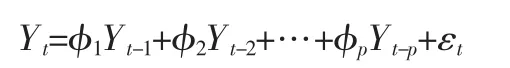
φ1，φ2，…φp为自回归系数；p 为自回归阶数，即模型中解释变量的个数。

1.2 移动平均模型（MA（q））

移动平均模型是仅用误差不同滞后项作为解释变量的模型，模型形式如下：

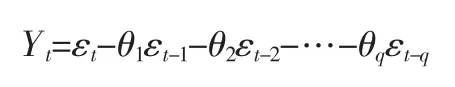
θ1，θ2，…，θq为移动平均系数；q 为移动平均阶数，即模型中解释变量的个数。

2 建立模型

2.1 数据预处理

2.1.1 平稳性检验

选取1978 年至2019 年的人均国民总收入数据进行平稳性检验。将数据导入Eviews 中作序列图（如图1 所示）。

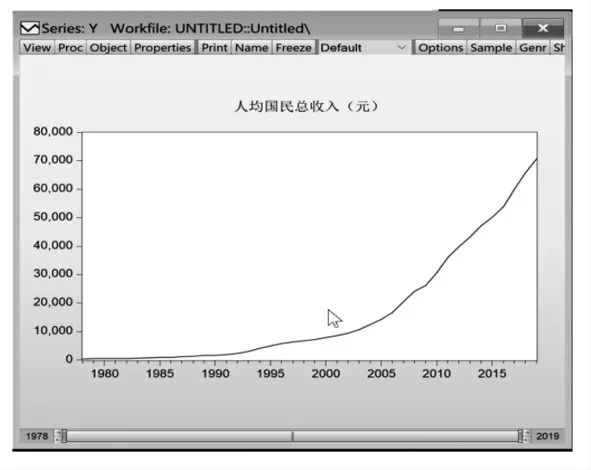
图1 平稳性检验

由图1 可以发现，原始序列存在上升趋势不平稳的现象，所以要进行平稳化处理。

2.1.2 平稳化处理

对原始数据进行一阶差分处理，得到一阶差分图，如图2所示。

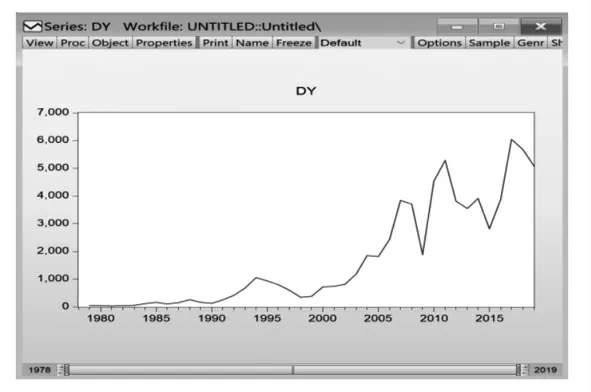
图2 平稳化处理

由图2 可知，一阶差分后的数据仍然不平稳，所以进行二阶差分（如图3 所示）。

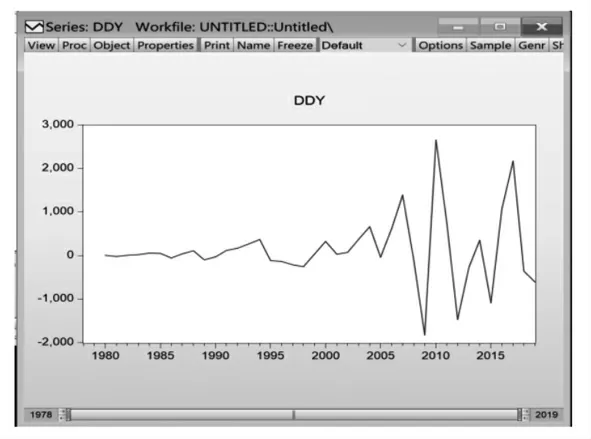
图3 二阶差分

由图3 可得，二阶差分后的数据基本都在0 值附近波动，我们初步认为二阶差分后的数据是平稳的。将二阶差分后的数据记为“DDY”，对DDY 进行单位根检验，得到T 统计量的值为－8.447 503，小于在1%的显著水平下的临界值－3.615 588。则T 统计量在1%的显著水平下拒绝原假设，所以人均国民总收入的二阶差分DDY 是平稳序列。

2.2 模型建立

2.2.1 模型识别

对序列进行平稳化处理后进行模型识别，根据平稳序列的自相关函数和偏自相关函数确定模型类别（如图4 所示）。

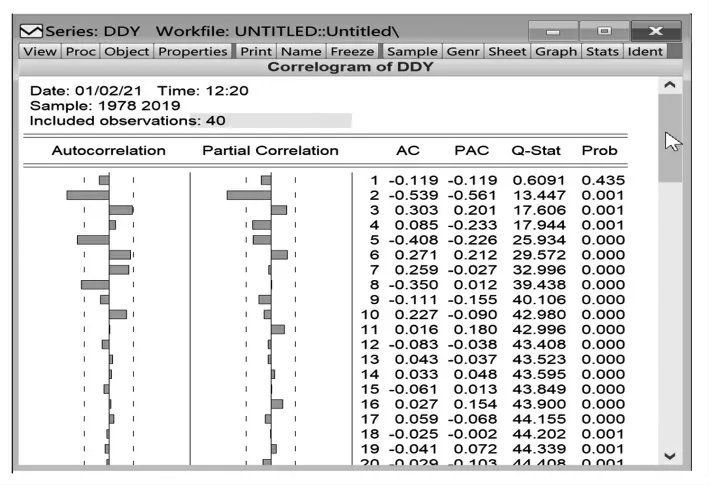
图4 模型类别

从图4 可以看出，偏自相关系数在滞后阶数k＝2 处显著不为0，在k＞2 时全部落入随机区间；自相关系数在滞后阶数k＝2时显著不为0，为了选择更好的模型，我们建立AR（2）模型、MA（2）模型进行比较。

2.2.2 模型建立

以下是AR（2）模型和MA（2）模型。

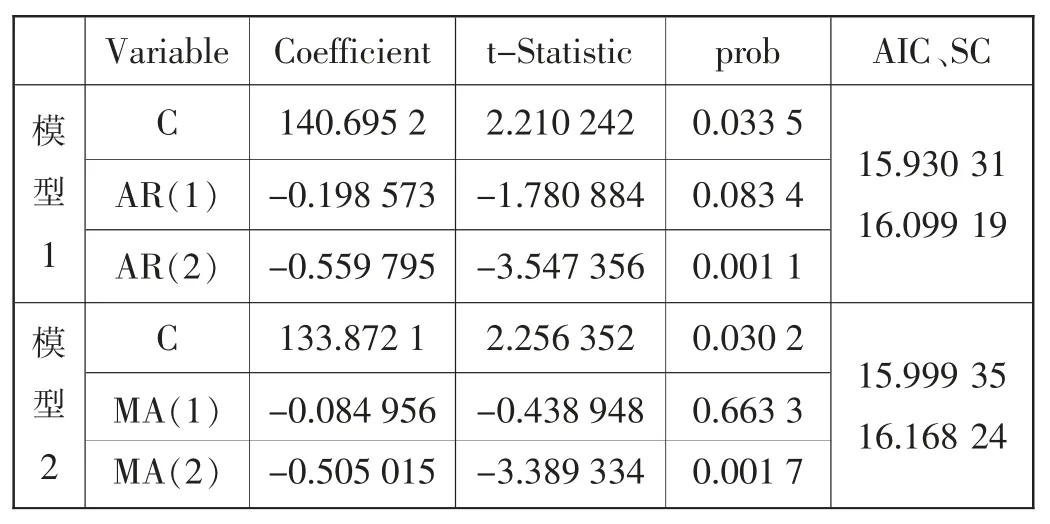
表1 模型比较

显著性水平小于0.05 的模型显著。模型显著之后，AIC 值和SC 值越小模型越好，我们选择阶数为2 的带常数项的自回归模型AR（2）。模型的表达式如下：

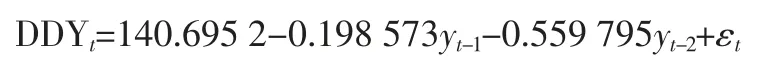
2.3 模型预测

利用上述模型对2020 年及2021 年人均国民总收入进行预测，预测结果为：2020 年人均国民总收入76 730 元，2021 年人均国民总收入83 209 元。2020 年的人均国民总收入较2019年高，2021 年的人均国民总收入较2020 年高。说明我国经济水平还将不断上升，人民生活富裕程度还将不断提高。

3 总结

经过高速发展，我国的经济总量包括国际地位有了明显的提升，经济总量稳居世界第二，但是人均水平却比较低。什么时候能够成为高收入国家，取决于未来我国经济增长速度、价格水平，取决于其他国家的增长情况等。所以，与其讨论能不能成为高收入国家，我们更重要的是要集中精力把经济发展好，把人民生活水平、收入水平提高，推动经济迈向高质量发展。提高居民收入永远只有进行时，只有不断提高居民收入，才能让人们的生活更幸福。