基于VMD-WPT和Prony算法的谐波间谐波检测

施瑶，王雅静，崔京楷，张涵瑞

（山东理工大学电气与电子工程学院，山东 淄博 255049）

随着各种新能源分布式电源的并网，电力系统受到的谐波间谐波污染加重，准确测量出谐波间谐波分量并对这些谐波分量进行处理对电力系统的安全可靠地运行具有重要意义[1-2]。

Prony算法能够快速准确地检测出谐波间谐波，在电力系统参数检测中应用广泛[3]。但Prony算法在检测中对噪声敏感，导致测量精度降低，需要降低噪声对Prony算法的影响。杜伟静[4]等人采用集合经验模态分解（ensemble empirical mode decomposition，EEMD）方法去除含有噪声的高频分量，但去除的高频分量中同样含有信号的有效信息，影响Prony测量精度。张煜林[5]等人采用互补总体经验模态分解（complementary ensemble empirical mode decomposition，CEEMD）联合小波包变换（wavelet packet transform，WPT）去噪，通过排列熵选取固有模态函数（intrinsic mode function，IMF）进行去噪，然而虚假分量的存在增加工作量，且忽略低频分量含有少量噪声的问题，影响Prony测量精度。

变分模态分解（variationalmode decomposition，VMD）算法是一种新的非线性信号处理方法[6]。VMD算法能够有效地克服EEMD分解过程中产生的虚假分量问题，且VMD算法相比于EEMD算法具有较好的噪声鲁棒性[7-8]。目前，VMD算法已经成功地运用在变压器局部放电去噪[9]、地震信号去噪[10]及轴承振动信号去噪中[11]。本文将VMD运用到电力系统的含噪谐波间谐波检测中，联合小波包变换（WPT）去噪，为降低噪声对Prony算法影响并提高检测精度提供一种新方法。

1 Prony算法原理

Prony算法通过对采样数据x(t)进行线性拟合得到一组复指数函数̂(t)，数学模型为

式中：p为模型阶数；N为采样点个数。

bi和zi的复数表达式为

式中：Ai为幅值；θi为相位；Δt为采样间隔；fi为频率；αi为衰减因子；j为虚数单位。

利用误差平方和ε最小原则保证拟合信号的准确度，表达式如下式所示：

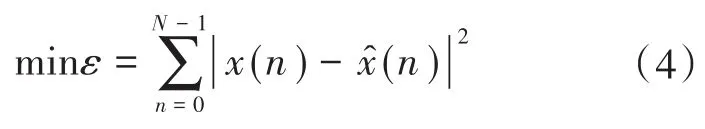
利用欧拉公式对式（1）进行求解可得下式：

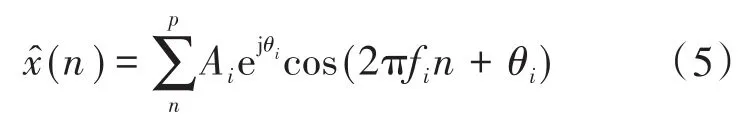
定义样本函数数学模型，如下式所示：

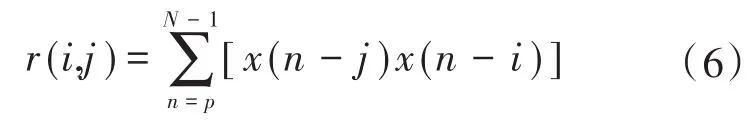
对式（6）进行构造扩展阶的样本矩阵Re，如下式所示：

利用奇异值分解和最小二乘法对式（7）进行求解，确定有效秩p和所有的特征方程系数a，并带入下式求解z：

将式（8）得到的结果带入式（1）并改写为下式的矩阵形式：

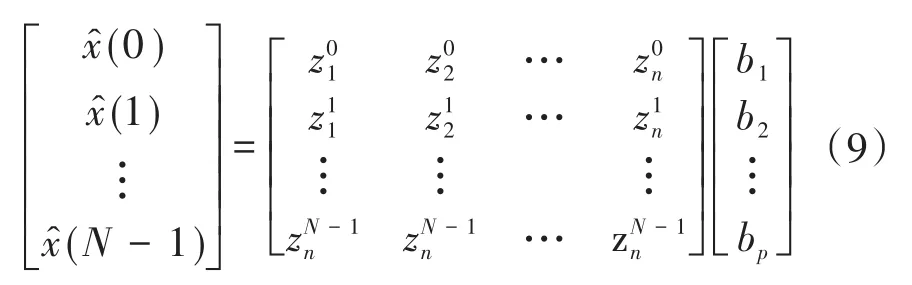
利用最小二乘法确定bi，并计算得到拟合幅值Ai，相位θi，频率fi，衰减因子αi。 具体计算公式如下式所示：

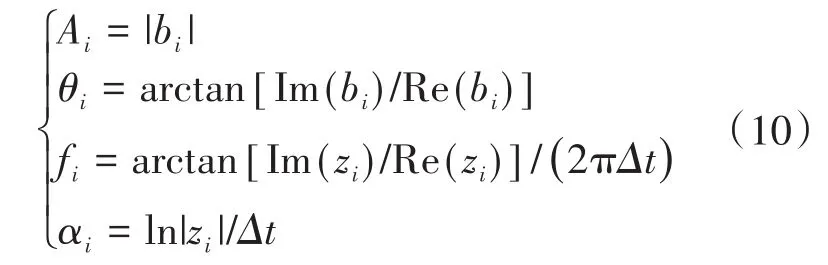
2 基于VMD-WPT和Prony算法的谐波间谐波检测

本文针对Prony算法对噪声敏感问题，提出了VMD-WPT联合去噪的算法模型，对含噪的谐波间谐波信号进行预处理，降低噪声对Prony算法检测精度的影响。

2.1 变分模态分解

谐波信号经过VMD处理分解为K个IMF分量信号，通过如下的方式估算每个IMF的中心频率和带宽：

1）利用对模态分量um进行Hilbert变换，m={1，2，3，…，K}，计算得到um(t)的解析信号；

2）加入指数项ejωmt估计每个解析信号的中心频率，并将um(t)的频谱调制到基频带上；

3）计算解调信号梯度的平方L2范数，估计带宽。

通过上述步骤得到的变分约束模型为

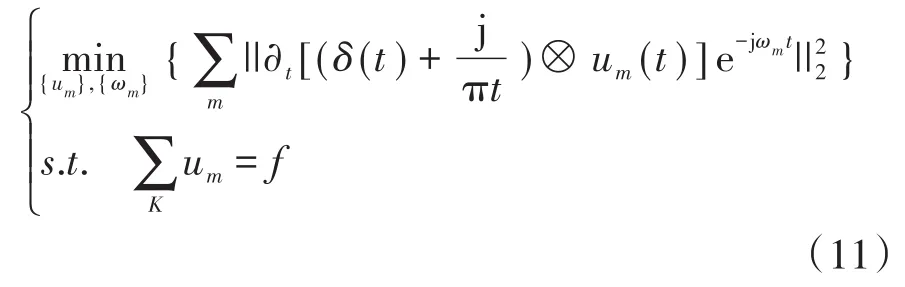
式中：δ(t)为单位脉冲信号；为卷积；∂t为对函数求时间t的偏导数；ωm为各模态分量中心频率。

通过迭代搜索变分模型并引入拉格朗日惩罚算子λ(t)和二次惩罚因子α将信号f分解成K个有限带宽的模态分量，各模态之和即为输入的信号。具体如下所述：

1）令n=0，并对做初始化处理；

2）令n=n+1，开始执行整个迭代；

3）令m=1，m＜K时，内层开始循环，更新um：

4）m＜K时，更新ωm：

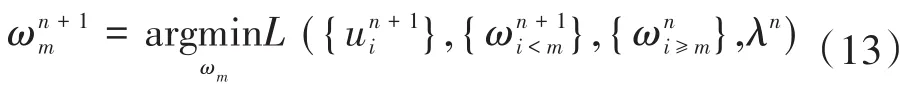
5）更新λ：

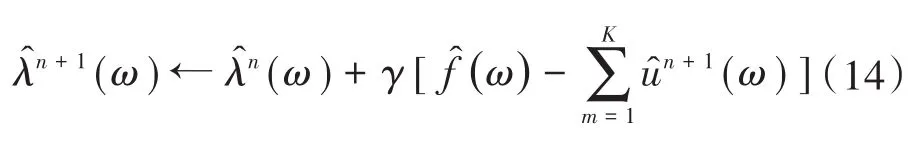
式中：γ为噪声容限参数，为降低噪声对分解结果影响，取γ=0。

6）循环步骤（2）～（5），直至满足下式迭代停止条件，结束循环：

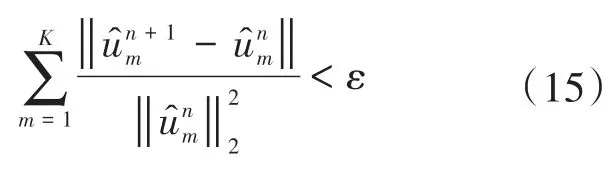
式中：ε为判别精度，且ε＞0。

通过上述步骤，VMD将信号分解为从低频到高频的K个IMF分量，其中噪声主要集中在高频分量上，低频分量中含有少量的噪声。

2.2 小波包降噪

文献[5]中张煜林等人利用小波包降噪方法对谐波信号经CEEMD分解得到的IMF分量进行降噪处理，本文在前人研究基础上采用小波降噪的方法对信号经VMD分解得到的IMF分量进行降噪处理。

小波包去噪的理论依据：含噪信号经过小波包分解后，代表有效信号的小波包分解系数幅值大于噪声的分解系数幅值，选择合适的阈值对有效信号幅值保留，将代表噪声的分解系数幅值设为零，并重构信号，获得去噪后的信号[12]。

小波包降噪的关键是选取合适的阈值，本文选择广泛运用的默认阈值μ，同时选择小波包软阈值去噪函数进行去噪处理，具体计算公式为

2.3 算法实现步骤

本文提出基于VMD-WPT的谐波和间谐波的去噪算法，利用Prony算法进行去噪后的信号电力系统参数的检测。通过以下步骤进行算法的参数辨识：

步骤1：对待处理信号进行VMD分解，得到若干个IMF分量。

步骤2：对得到的IMF分量进行小波包软阈值去噪，并重构IMF分量。

步骤3：叠加去噪后的IMF分量，得到去噪处理后的信号，并利用Prony算法分析参数。

通过上述步骤即可实现本文算法的谐波间谐波参数的检测。

3 算法仿真与比较

3.1 算例1

采用与文献[4]相同的谐波间谐波信号模型与参数，信号的模型如下式所示：

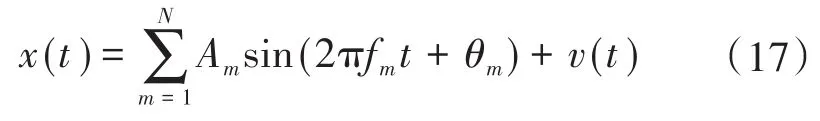
式中：v(t)为噪声。

信号的具体参数如表1所示，且加入v(t)后信号的信噪比为20 dB。

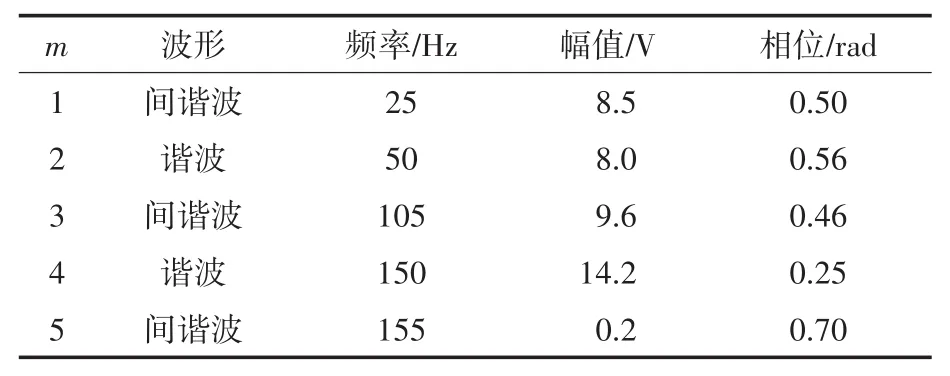
表1 模型参数设置Tab.1 Model parameter setting

采样频率4 000 Hz，采样点数为1 000，采样长度为0.25，含有噪声的信号波形如图1所示。

图1 含噪信号波形图Fig.1 Waveform of noisy signal

利用VMD算法和文献[4]中EEMD算法分别对含噪的信号进行分解，得到的IMF分量波形图，如图2、图3所示。

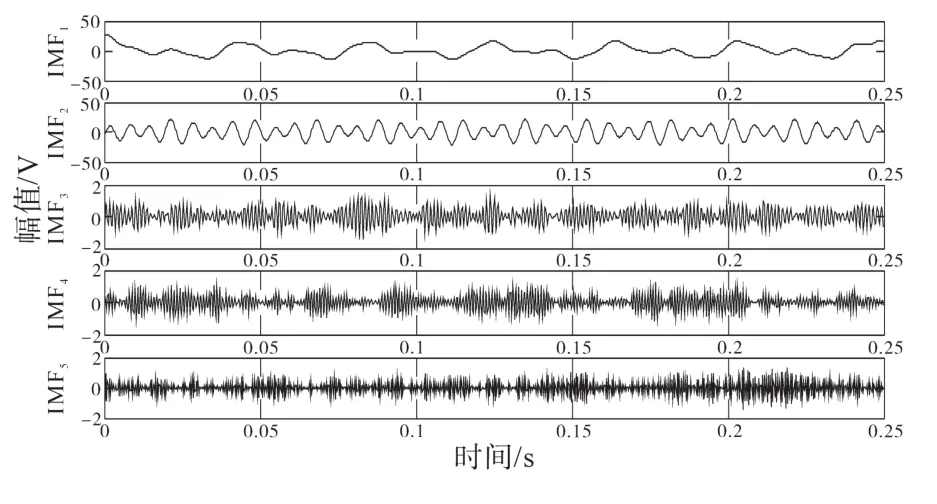
图2 含噪信号VMD分解Fig.2 Noisy signal decomposition based on VMD

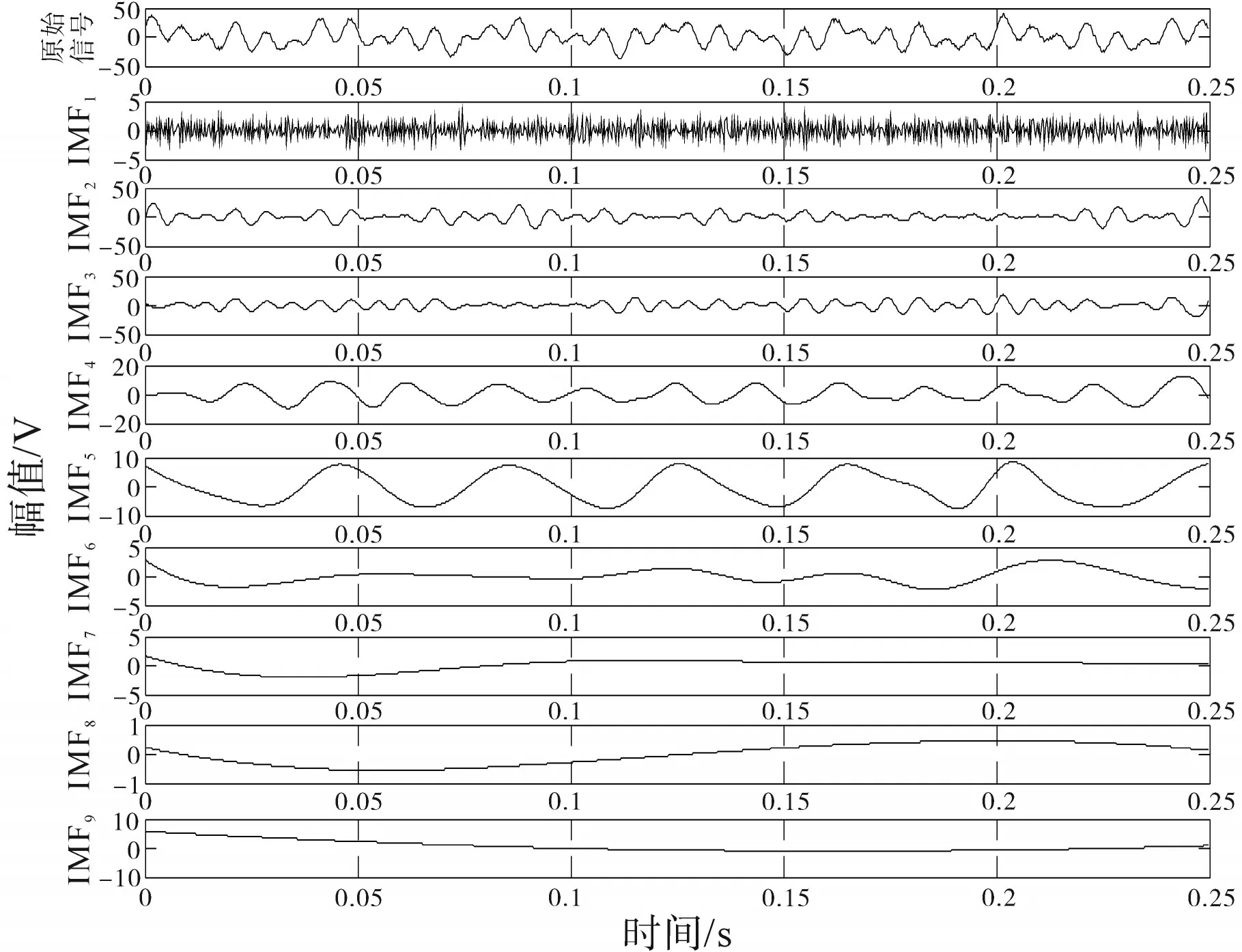
图3 含噪信号EEMD分解Fig.3 Noisy signal decomposition based on EEMD

由图3可知，文献[4]利用EEMD算法进行含噪信号的分解得到的IMF存在虚假分量。通过排列熵的方法进行有效信息分量的筛选，然而排列熵的选取阈值需要通过大量的实验测量才能确定，缺乏理论依据，容易受到人为因素的干扰，不能准确得到含有噪声的有效信息分量，同时也忽略了低频分量同样含有少量噪声，影响后续参数辨识准确度。

比较图2、图3可知，VMD算法有效地避免了虚假分量的产生，降低计算量以及人为因素的干扰。VMD算法虽然具有一定的抗噪性，但是所得到的IMF分量，受到噪声干扰，波形发生了严重的畸变。对得到的IMF分量进行小波包去噪处理，去噪处理后的IMF分量波形如图4所示。

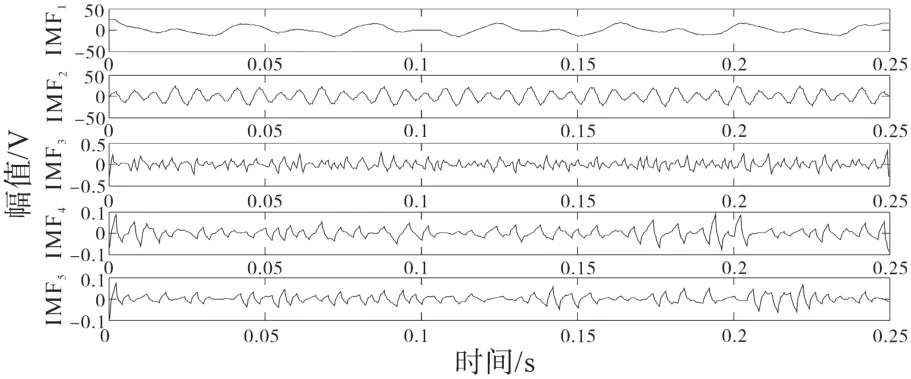
图4 IMF分量小波包降噪Fig.4 IMF component denoised based on wavelet packet

改变竖轴的尺度便于直观观察IMF分量去噪的效果。叠加去噪后的IMF分量重构信号，得到去噪后的谐波间谐波信号，并与原始信号波形图进行比较，比较结果如图5所示。由图5信号波形图比较可以较为直观地观察谐波和间谐波信号去噪的效果。对去噪算法质量进行评价，主要针对运算速率与去噪效果两个方面。评价算法的运算速率，首先从数据结构方面计算算法整体复杂度，文献[4]的EEMD-RobustICA算法时间复杂度为O（n4），空间复杂度为O（1）；文章采用VMD-WPT算法的时间复杂度为O（n3），空间复杂度为O（1），显然文献[4]算法的时间复杂度大于文章的算法。运行两个算法分别对信号进行降噪处理，文献[4]算法所需时间为4.573 s，而文章算法需要3.043 s，比较可知文章算法计算耗时短，能够实现信号去噪的快速处理。

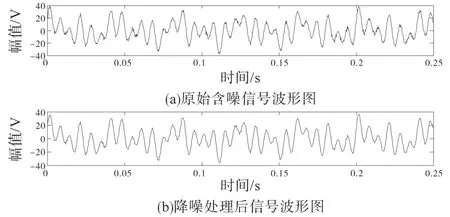
图5 信号波形图比较Fig.5 Comparison of signal oscillogram

针对算法去噪效果比较，引入均方根误差（RMSE）、信噪比（SNR）、信号相关系数（R）三个指标进行评价[11]。当信号的RMSE越小、SNR越大时，去噪效果越好。相关系数反映了去噪后的信号与原始信号的相关程度，R越大越接近原始信号。将本文与文献[4]中采用的去噪算法进行比较，比较结果如表2所示。

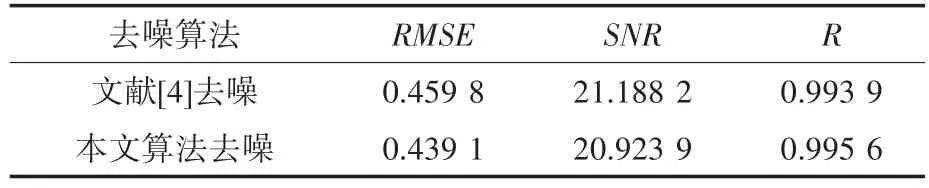
表2 去噪效果评价Tab.2 Evaluation of denoising effect

从表2中可知，本文的SNR略低于文献[4]去噪方法，但是RMSE相较于文献[4]提升了4.5%，信号的相关系数R也有一定的提升，表示信号在去噪过程中更好地保留了有效信息。综合评价，文章去噪算法要优于文献[4]的算法。

含噪的谐波与间谐波信号经过本文算法降噪处理后，利用Prony算法对信号的频率、幅值、相位进行检测，具体检测结果如表3所示。

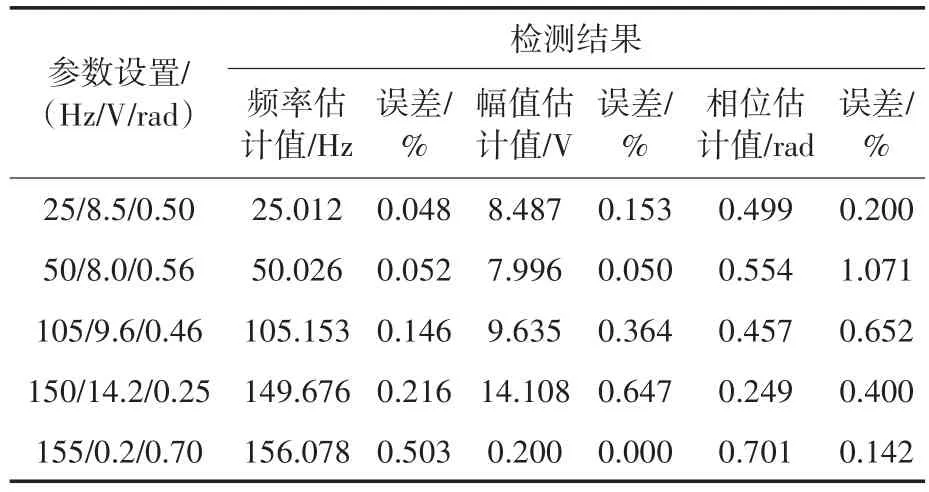
表3 Prony算法参数辨识结果Tab.3 Parameter identification results of Prony algorithm

从表3的数据可以看出，利用Prony算法对降噪处理后的谐波和间谐波信号检测的频率、幅值、相位的平均误差为0.193%，0.243%，0.493%。显然通过VMD-WPT算法降噪的Prony算法在含噪的电能质量参数检测中是有效的，且具有良好的检测精度，文章提出的VMD-WPT降噪算法能够有效抑制噪声对Prony算法的影响。

3.2 算例2

采用与文献[5]相同的数学模型与参数设置，加入噪声后信号的信噪比为40 dB，利用本文算法进行谐波间谐波参数检测，与文献[5]中参数检测结果进行对比，通过检测结果直接观察算法的去噪效果。检测结果如表4所示。

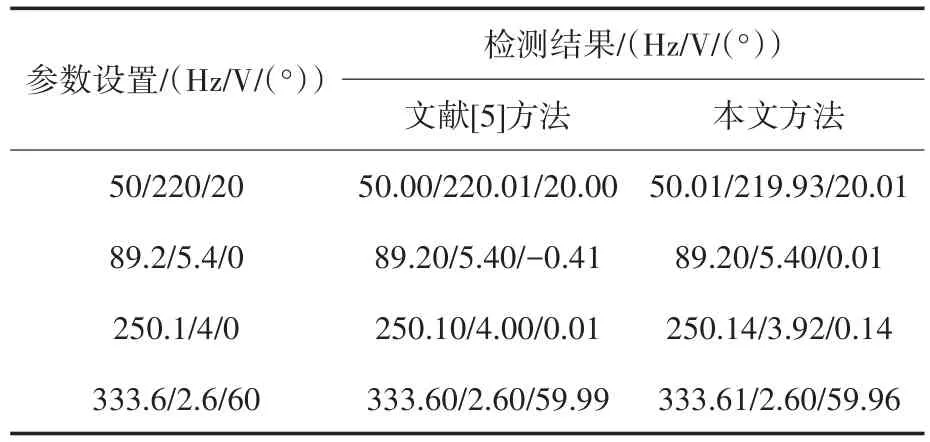
表4 文献[5]方法与本文方法参数辨识结果对比Tab.4 Comparison of parameter identification results between literature[5]method and the proposed method

从表4的检测结果可知，文献[5]方法与本文方法都能有效地降低噪声对Prony算法影响，频率与幅值的检测结果与原始数据相近。相位检测中，本文算法相较于文献方法在低频分量相位检测结果更加接近原始数据。

对比两种算法计算耗时，文献[5]算法计算所需时间为3.202 s，而本文算法计算所需时间为2.976 s，显然本文算法计算耗时更短，且文献[5]计算耗时是在已经选取合适的排列熵值前提下得到的，在检测过程中，合适的排列熵值需要大量计算并人为选取，实际所耗费时间远大于本文算法，且可能存在主观因素的干扰。

从算法计算耗时与去噪效果两个方面综合评价，本文提出的算法要优于文献[5]的算法。

3.3 算例3

为进一步验证本文算法的有效性与准确性，采用文献[13]的数学模型及参数设置，在信噪比为40 dB的情况下利用本文的算法进行检测，并与文献[13]的检测结果进行对比，结果如表5所示。

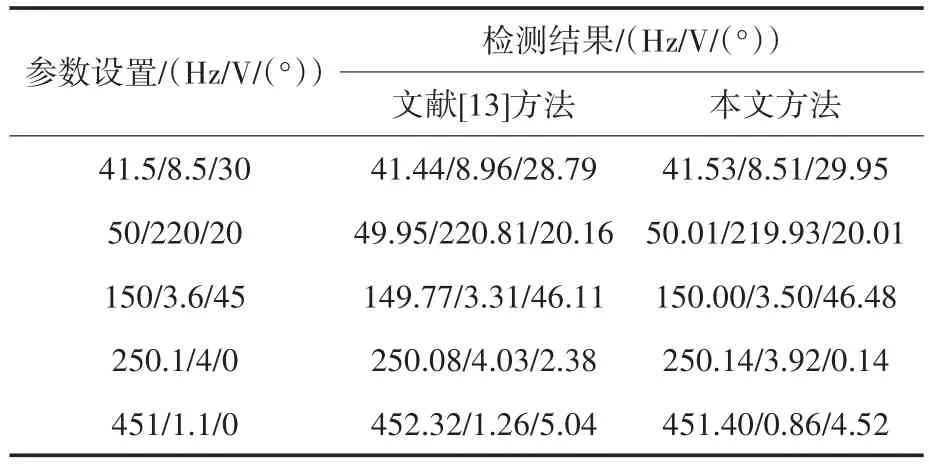
表5 文献[13]方法与本文方法参数辨识结果对比Tab.5 Comparison of parameter identification results between literature[13]method and the proposed method

从表5的数据可以看出，文献[13]采用的Root-MUSIC与Prony检测算法拥有较好的检测精度，但由于噪声的影响，在41.5 Hz与250.1 Hz时，相位出现了较大的误差。本文算法降低了噪声的影响，检测出的结果更接近原始数据，尤其在相位的检测上有着更好参数辨识效果，提升了Prony算法在含噪电能质量检测中的精度。因此，本文提出的VMD-WPT和Prony算法在含噪谐波间谐波的检测方面是有效的，且具有良好的检测效果。

4 结论

VMD算法被广泛地运用在其他领域的去噪中，本文在前人的基础上将VMD算法引入谐波间谐波信号去噪中，并与WPT算法联合，提出了VMDWPT联合去噪的算法模型，降低了噪声对Prony算法的影响。仿真与比较结果验证了本文算法的有效性，且具有良好的检测精度，为Prony算法在含噪的谐波与间谐波检测中提供一种新思路。