基于四桥臂逆变器的PMSM断相容错控制策略

袁高龙，向保林，徐光辉

（1.武汉电力职业技术学院输配电培训部，湖北 武汉 430070；2.湖北工业大学电气与电子工程学院，湖北 武汉 430068）

永磁同步电机（PMSM）以其高效率、高响应速度等优势被广泛应用于对可靠性有严格要求的领域，如航空航天、电力系统以及船舶推进系统等[1-2]。近年来PMSM断相故障受到越来越多的关注。当电机的任一相或逆变器的任一桥臂完全断开时往往会出现断相故障。在断相故障下，由于相电流不平衡，会降低电机的性能和效率，并且在极端情况下可能导致不可恢复的损坏[3]。

根据电机的相数，容错方法可以分为多相电机容错和三相电机容错[4]。与传统的三相电机相比，多相电机可以通过相数冗余增加控制自由度来提高驱动系统的容错能力，且无需其他硬件[5]。但是多相电机的设计和控制复杂，并且多相电机的应用范围更窄[6]。因此研究工业应用中三相永磁同步电机的断相容错方法具有重要意义。

针对PMSM断相容错，文献[7]提出空间矢量控制方法，即通过故障相信号对中线进行控制，将d，q轴电流比例积分控制器的输出端设计为前馈d，q轴补偿电压，进而对因断相故障导致的转矩脉动进行抑制。但是该方法的前馈d，q轴补偿电压是根据理论模型得到的，系统参数的设置对其补偿效果影响较大，故鲁棒性较差。文献[8]在电机断相故障发生后通过新坐标变换来使其d，q轴电流解耦，进而对单相故障后的转矩脉动进行控制，但是该方法采用母线电容作为非故障相独立控制的回路，故要求母线电容具备一定的承载能力。文献[9]主要研究四桥臂驱系统的断相故障，通过非故障相电压控制来实现断相故障后的电机容错，该方法具有一定的控制效果，但是抑制后的转矩脉动还存在波动性，从而导致电机运行稳定性不强。文献[10]提出的电机断相容错控制方法是基于电机定子绕组合成磁动势恒定而实现的，即在断相故障后对非故障相的电流相位及幅值进行重新配置，同时将滞环控制器引入到旋转坐标系下，保证了断相故障情况下的电机运行的稳定性。该滞环控制器可以对非故障相的电流进行跟踪控制，但是该方法存在开关频率不稳定的问题。文献[11]针对星形联结的永磁同步电机提出一种基于四桥臂拓扑的断相容错控制策略，通过利用相补偿电流与零轴电流的等效关系，计算出零轴电流参考控制量，并根据期望的动静特性设计出零轴电流闭环内模控制器，从而实现零轴电流的高精度跟踪控制，但是该方法中d，q轴电流计算较为复杂。

鉴于此，针对三相PMSM出现的断相故障提出了一种新的基于四桥逆变器的PMSM断相容错控制方法。首先根据断相后电压、电流之间的关系构建PMSM容错数学模型，并推导出断相后模型的输入输出方程。其次，根据新的坐标变换矩阵，将d，q轴电压/电流参考值转换为两个无故障相的相电压/电流，从而将电流控制器（PI控制器）直接切换到故障后状态，而无需重新设计控制器。另外，利用基于载波的PWM来驱动断相的PMSM，从而实现电机的容错控制。对比实验结果验证了所提出的断相容错系统具有更强的容错能力。

1 三相四桥臂PMSM容错数学模型

针对三相四桥臂PMSM，其故障类型主要体现在绕组和功率管两方面，其故障拓扑结构如图1所示。

图1 三相四桥臂PMSM的故障拓扑结构Fig.1 Three-phase four-arm PMSM fault topology

在正常情况下电机驱动器使用三桥臂逆变器运行，且未连接零线。当系统发生单相绕组断路故障时，断路相绕组电流为0；当发生单相功率管断路故障时，该相绕组电流为正弦半波。因此通过实时采样绕组电流即可对单相断路故障进行故障辨识；当发生单相绕组短路故障时，短路相绕组所在逆变器控制的电机绕组中心点电位发生畸变，正常工作时中心点电位为是0.33Udc或0.67Udc，其中Udc为直流母线电压。短路故障时中心点电位变成0或Udc，因此通过实时监测中心点电压即可实现绕组短路故障辨识；当系统发生单相功率管短路故障时，会发生功率管直通现象，因此通过实时监测功率管直通故障信号即可辨识功率管的短路故障。

在正常工作条件下，a-b-c固定坐标系中的PMSM模型如下式所示[12]：

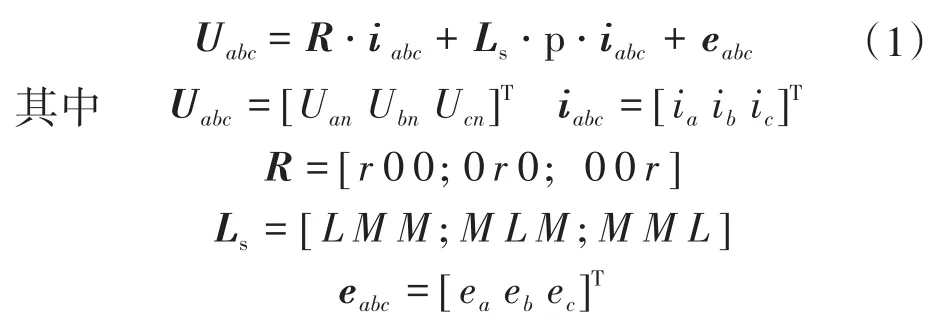
式中：Uan，Ubn和Ucn为a-b-c坐标系中三相的端电压；ia，ib和ic为a-b-c坐标系中电机的相电流；p为微分运算；R为电阻矩阵；Ls为电感矩阵；eabc为相位反电动势；M为耦合系数。

一般情况下，通过Clarke和Park变换可以将三相固定坐标系中的相电流（ia，ib和ic）转换为同步坐标系中的直流变量（id和iq）[13]。比例积分（PI）控制器用于调节电机电流，PI控制器的输出参考电压U*d和U*q可以转换为U*α和U*β以驱动三相逆变器（或在基于载波的PWM中转换为上述的转换都可以通过Clarke和Park转换及其逆矩阵来实现，如以下2式所示：

其中

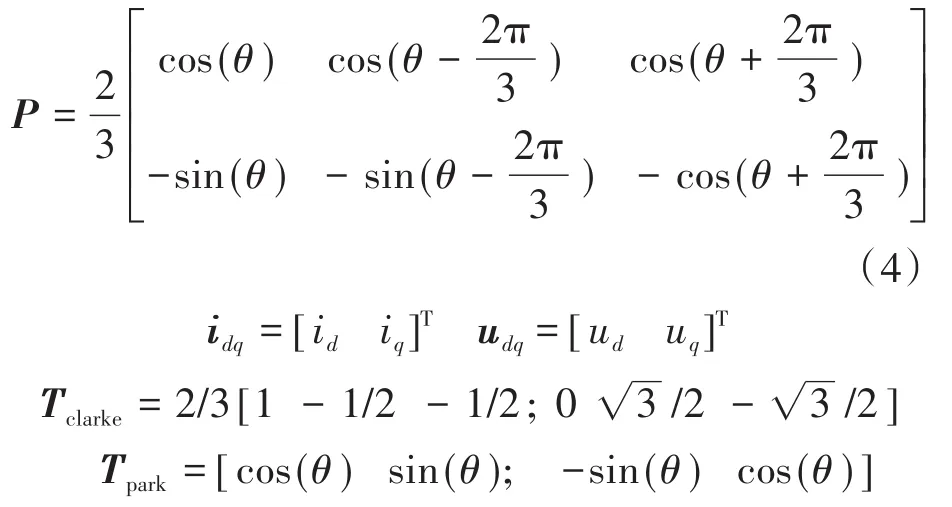
式中：P为a-b-c→d-q坐标系变换矩阵；θ为转子位置；id，iq为d-q坐标系中电机电流；ud和uq为dq坐标系中电机电压；Tclarke为克拉克变换矩阵；Tpark为Park变换矩阵。

从d-q坐标系到a-b-c坐标系的逆变换由以下2式来实现：

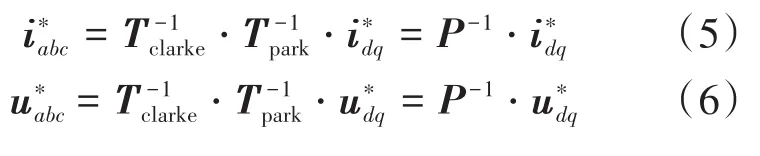
其中

式中：P-1为d-q→a-b-c坐标系的变换矩阵；“*”为参考值为Park逆变换矩阵；为Clarke逆变换矩阵。

假设A相开路，此时ia=0，当出现断相故障时，A相不会产生电磁转矩。将式（2）和式（3）中与A相有关的项次删除后，式（2）和式（3）可转换为

其中

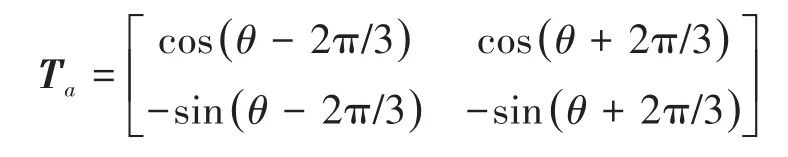
式中：Ta为b-c→d-q坐标系的变换矩阵。

同样，如果忽略式（5）和式（6）中与A相有关的项次就可以得到d-q→b-c坐标系的逆变换如下：

当A相发生断相故障时，电压方程式（如式（1））可简化为

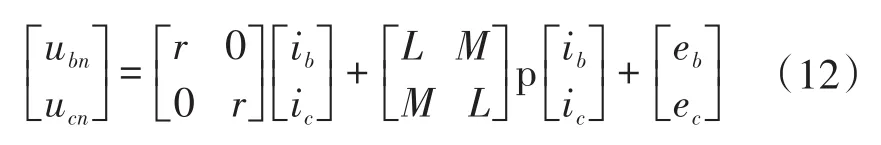
如果PWM电压源逆变器的非线性（PWMVSI）可以忽略，那么在断相条件下，电机电压应等于其参考电压，即：

将式（12）中的电机电压用参考值代入后，式（12）可变换为

为了分析d-q坐标中电压和电流的关系，将具有传统变换矩阵的断相PMSM进行坐标系转换。将式（14）中的电压用式（11）代入，式（14）中的电流ibc用式（8）代入，就可以得到断相PMSM的输入输出方程式如下：

从式（8）和式（10）可以看出，矩阵Ta和的乘积并不是单位矩阵。如果将传统的Clarke和Park变换矩阵应用于断相电机中，那么广义的断相PMSM电压方程（如式（15））将非常复杂，并且其非线性也将更加突出。此外，如果使用PI控制器，其控制性能也将下降。因此在断相故障的情况下，新的电压/电流坐标系的变换矩阵尤为重要，如图2所示。

图2 断相故障的PMSM控制系统Fig.2 PMSM control system of phase failure

2 三相PMSM容错控制策略

2.1 电压/电流坐标变换矩阵

为保持断相PMSM的磁动势和电磁力矩不变，应将d，q轴的电流作为故障前的电流。因此在出现断相故障后，其余两相必须产生相同的d，q轴电流。假设A相出现断相故障（如图1b所示），则电机工作在不平衡状态（ia=0）。在这种情况下ia不可控，只有B相和C相才能产生有效转矩。因此为了获得与故障前相同的d，q轴电流，应调整B相和C相预期的相电流。根据式（8）可以通过对矩阵Ta求逆来获得B相和C相的校正电流指令如下式：

类似地，通过下式得到b-c坐标系中相电压的校准值为

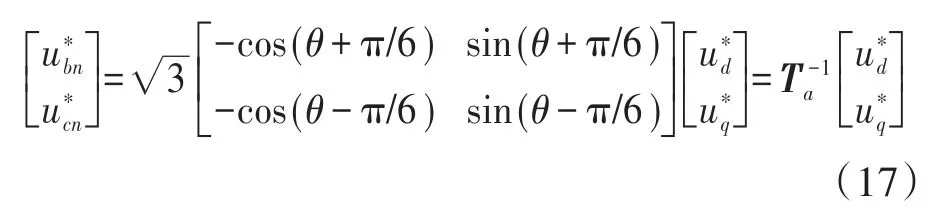
利用新的变换矩阵（Ta和T-1a），可将式（15）简化为

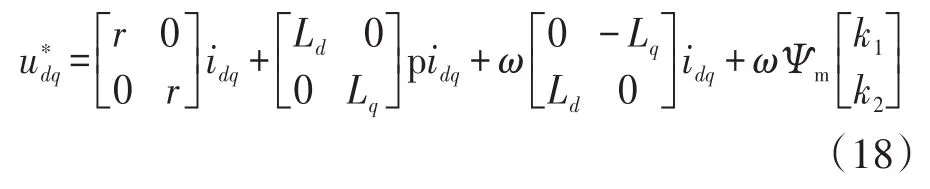
对于有效的PMSM控制系统而言，d，q轴的电压方程式可以写为

比较式（18）和式（19），可以发现故障状态下的电压方程式与正常状态下的电压方程式相似。式（18）和式（19）的主要区别在于式中的反电动势，且两式的最后两项可以被当成干扰项。因此正常情况下电机的干扰项可以写成：

断相电机的干扰项可以写为

各施工工况下对H型钢主结构和凸起椭圆拱形结构的位置必须进行跟踪测量，施工时应采取必要的措施，使变形在受控下完成，以保证整体造型和施工质量。

从式（20）和式（21）中可以得到，故障前后两个干扰项的波形相似，并且具有几乎相同的数量级。尽管故障后的干扰幅度稍大，但可以接受。因此，电流控制器可以设计为PI控制器，且可以通过前馈补偿的方法来消除这些干扰。

同样，也可以获得B相和C相开路下的变换矩阵，变换矩阵的方程式如下所示：

式中：下标x，y为余下相位；下标z为断相；k为相位调整系数。

当z=a时，x=b，y=c，k=0；当z=b时，x=c，y=a，k=2；当z=c时，x=a，y=b，k=1。当出现断相故障时，iz=0。在反馈回路中，矩阵P（a-b-c→d-q）和矩阵Ta（x-y→d-q）产生的变换结果相同。iz=0可以看作Clarke和Park变换中的特例，因此变换矩阵P也可以应用在断相PMSM系统的反馈回路中，但是应将电流回路中正向路径的变换矩阵P-1替换为矩阵T-1z，从而避免断相故障下的非线性影响。

2.2 基于载波PWM的断相PMSM驱动方法

在定子绕组的断相故障下，三相绕组中的一相不可用，因此传统的SVPWM方法无法获得三个独立的电压[14]。考虑到基于载波的PWM方法可以产生三个独立电压，因此本文采用载波PWM来驱动PMSM。对于具有载波PWM的PMSM来说，三相端子的参考电压和中线参考电压如下式所示：

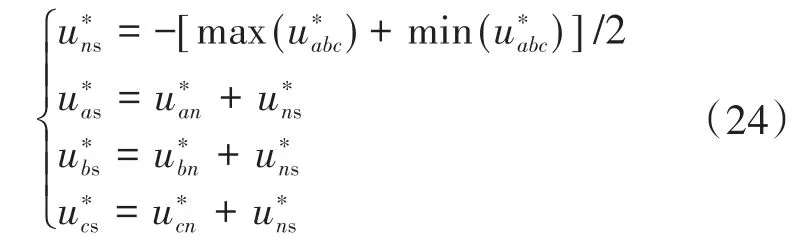
在断相条件下，与断相相对应的电源开关处于受控关断状态，其余相的端子参考电压和可以根据式（23）计算。考虑到偏置电压的设计原理是使电源的电压利用率最大化，因此可以将偏置电压指令设置为

图3为正常状态和断相故障状态下的PMSM控制系统框图。该控制系统主要包括七个模块：电流PI控制器、同步坐标系变换、PWM发生器、四桥臂逆变器、PMSM、相位故障诊断和逆坐标转换。相位故障诊断模块通过监视相电流来输出故障符号（F）和故障位置（z）。如果电机在正常状态下运转，可以将常规的变换矩阵P（a-b-c→d-q）用于电机的电流变换中以获得d，q轴的反馈电流。通过调节电流PI控制器，就可以产生d，q轴的控制电压再通过变换矩阵转换为控制电压最后通过 SVPWM 调制从而驱动电机。当发生断相故障时，采用新的逆变换矩阵来获得控制电压并且利用基于载波的PWM来产生驱动逆变器的指令。可以发现，两个矢量控制器的主要区别在于电流环路正向路径中的逆变换矩阵和PWM调制方法，在正常状态和断相故障状态下其它模块没有差别。

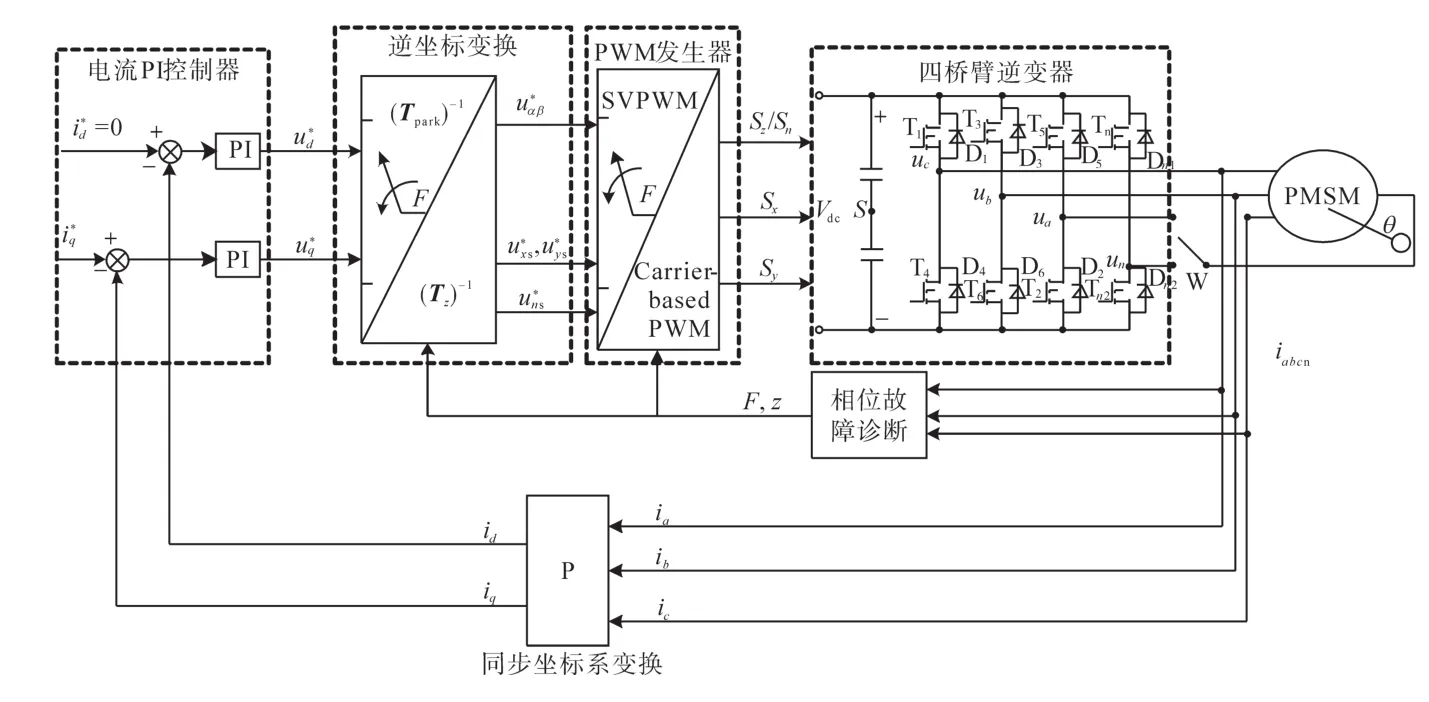
图3 容错控制方案Fig.3 Fault-tolerant control scheme

3 实验结果与讨论

3.1 实验设置

为了评估所提方法的性能实验中使用了坐标转换方法，并借助双框架控制力矩的陀螺仪（DGCMG）原型。其主要参数如下：直流电源Udc=28 V，转动惯量J=0.173 kg·m2，反电动势系数Ke=2.22 N·m/A，相电阻R=6 Ω，相电感L=9 mH，角动量H=10 N·ms。框架电机的转矩控制系统采用id=0的控制方式。

3.2 断相容错方法比较

为了验证所提出的断相容错方法的优越性，在电机运行期间必须将A相从逆变器上断开。在系统无容错、具有电压前馈补偿和本文所提方法之间进行了对比实验。图4为无容错补偿措施实验结果。从图4中可以看出，在断相故障后，A相的电流立即减小到零，而由于反电动势的原因，A相的检测电压不为零。

图4 无容错补偿措施Fig.4 Compensation measures without fault tolerance

图5、图6分别为传统前馈电压补偿控制策略、本文提出控制策略的实验结果。为了提高断相永磁同步电机的性能，在系统中采用了基于前馈电压补偿的容错方法。前馈电压根据文献[8]计算，为了获得准确的前馈电压，应预先获取电机参数，例如永磁磁链Ψm、定子直流、正交和漏电感Id，Iq，Iσ。

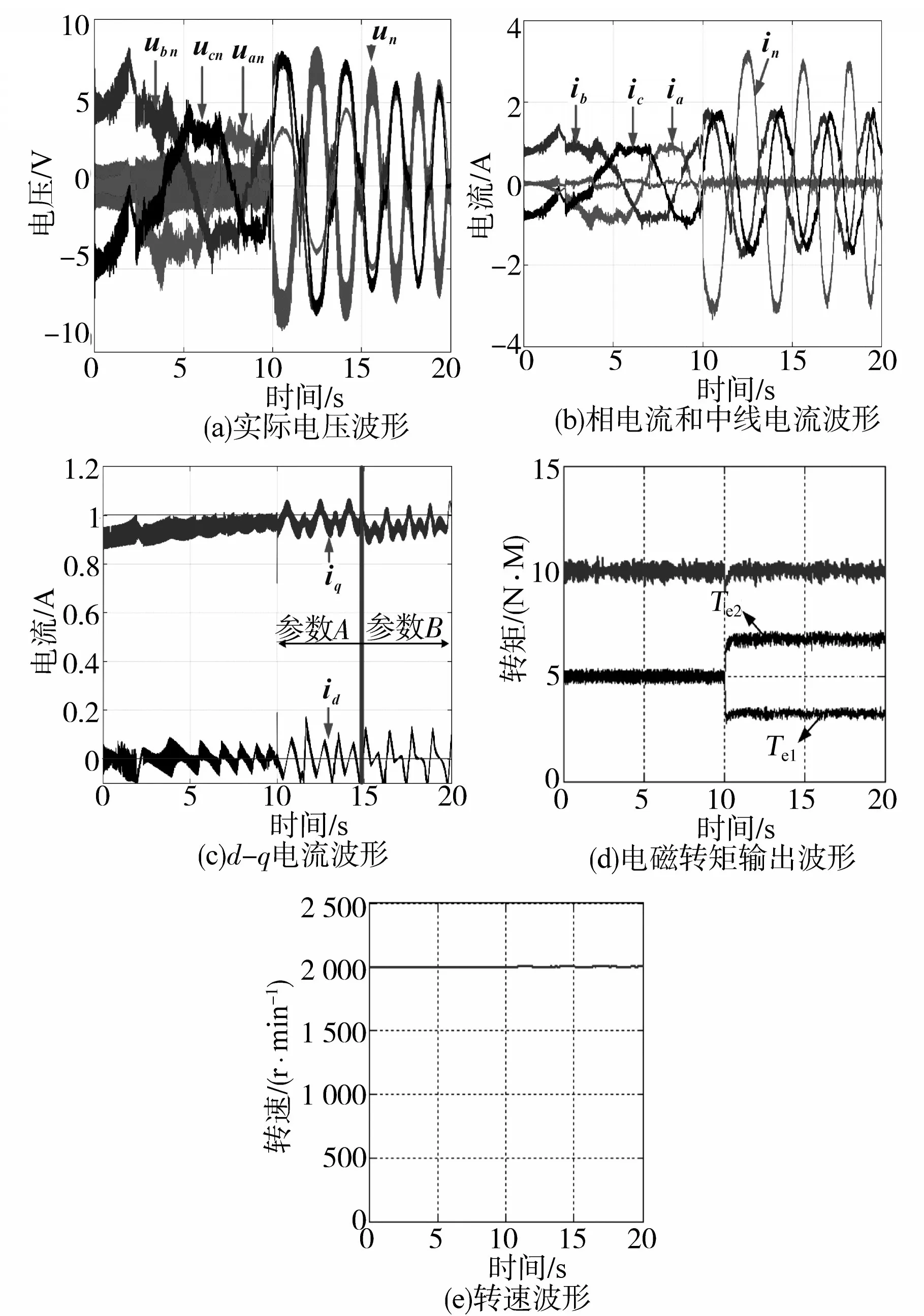
图5 传统前馈电压补偿控制策略Fig.5 Traditional feedforward voltage compensation control strategy

图6 本文提出的控制策略Fig.6 The control strategy proposed in this paper

从图5可以看出通过前馈补偿，d-q电流性能得到改善，并且q轴电流波动从0.185 A减小到0.156 A，另外从电磁转矩输出波形和转速波形上来看其性能均有所改善。但是由于补偿中忽略了电感和相电阻的变化，因此其作用是有限的。除此之外，对前馈电压补偿中电机参数错误也进行了测试。当电机参数不正确时，补偿性能会降低。如图5所示，当电机参数改变50%（参数B），d，q轴的电流误差会增加。由此可以发现，基于前馈电压补偿方法的性能会受到电机参数精度的影响。

从图6可以看出，与断相电机系统和前馈电压补偿系统相比，q轴电流波动明显减小。尽管d轴的电流波形中存在波动，但因为PMSM的转矩表达式中d轴的电流系数为零（Ld=Lq），因此不会影响电机的性能。另外，经过本文所提出的容错控制策略后，其电磁输出转矩和转速较前馈电压补偿控制策略更为稳定。

3.3 加速和反转性能测试

在此实验中，利用断相PMSM加速和反转来测试提出的容错方法的性能。针对加速性能测试，在t=15 s之前，设定参考电流为0.3 A，15 s后将参考电流设置为在t=8 s时，断开A相，并将所提出的容错策略应用于系统中。在正常状态下，电机由三相逆变器驱动，一旦断开了A相的定子绕组，便会激活第四桥臂。图7为所获得的相电流、d-q电流和断相PMSM的速度示意图。

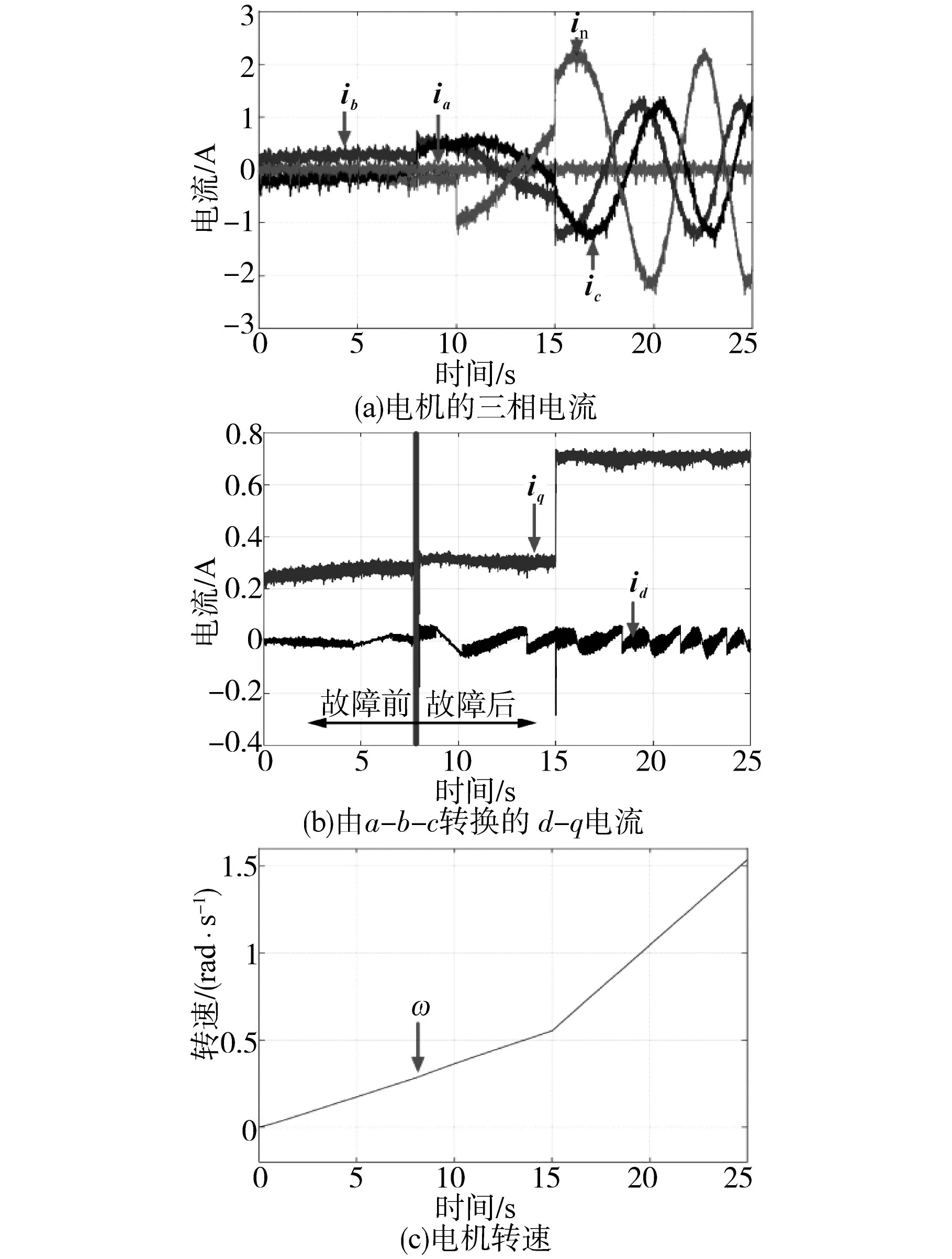
图7 三相PMSM的加速性能Fig.7 Acceleration performance of three-phase PMSM

由图7可知，当断相电机加速时，叠加在电机电流上的波动很小，并且电机速度波形较为平滑。

在断相电机的反转性能测试中，在t=15 s之前，设定参考电流为15 s后将参考电流设置为在t=8 s时，断开A相，并将所提出的容错策略应用于系统。图8为断相PMSM的相电流、d-q电流和PMSM速度波形图。由图8可知，尽管故障发生时瞬时的速度波动很小，但是断相电机在其反转操作中可以很好地运行。

图8 断相PMSM的反转性能Fig.8 Reversal performance of phase-off PMSM

3.4 稳态性测试和FFT分析

在该实验中，对所提出的容错方法进行了稳态性测试和FFT分析。由于DGCMG框架的额定速度和额定电流相对较低，因此使用了功率较大的PMSM进行测试。

实验中断开A相，并将t=5 s之前的电流基准设置为，5 s后将电流基准设置为产生的三相电流波形和dq电流波形如图9a和图9b所示，从电流波形中可以发现，所提出的断相容错方法具有很好的稳态性。图9c为d-q电流的FFT分析图，根据d，q轴电流的谐波特性，可以发现所提出的容错方法具有较低的总谐波失真（THD）。

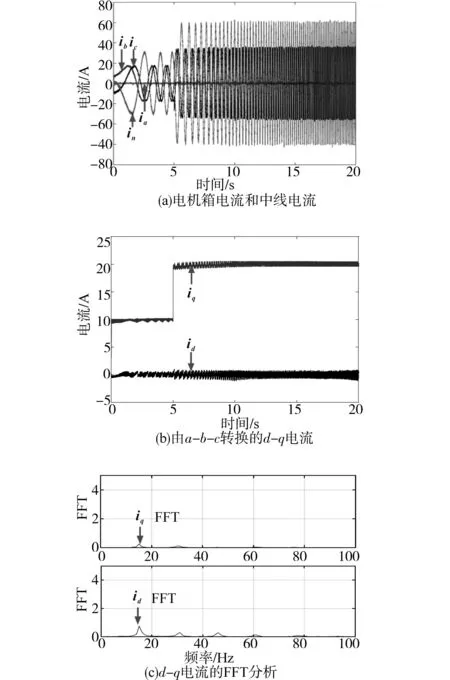
图9 稳态性能测试和FFT分析Fig.9 Steady-state performance test and FFT analysis

4 结论

为了改善断相故障后电机性能，提出了基于四桥臂逆变器的PMSM断相容错控制策略。与传统的容错方法不同，该容错方法不需要重新设置控制器或进行前馈电压补偿，特别是当发生断相故障时，PI控制器参数可以保持不变。另外，由于容错方法是基于四桥臂逆变器设计的，因此与基于三相逆变器的方法相比，可以获得更高的容错能力。

实验结果表明本文提出的断相容错控制策略具有良好的稳态特性以及较低的总谐波失真。需要注意的是，三相四桥臂电机的容错控制重点之一在于如何利用硬件设计来实现单相绕组故障和功率管故障的开关切换，因此本文后续将重点研究不同单相故障的开关切换问题。