基于二阶广义积分器的LCL型并网逆变器延时补偿方法

张竣淇，康朋，田昊，马磊，冯婷婷，刘松松

（国网重庆市电力公司经济技术研究院，重庆 401120）

分布式发电技术作为应对能源紧缺、解决环境污染的重要手段之一，在国家的电力能源发展中发挥了举足轻重的作用[1-2]。LCL型并网逆变器作为分布式发电系统中最为关键的装置之一，能实现交直流的快速转变与公共电网的功率馈入，受到了较多学者和专家的重视[3-4]。但由于LCL滤波器存在谐振现象，若不额外引入阻尼对其进行抑制，系统将难以稳定[5-6]。

因此，对于LCL滤波器的谐振抑制，有学者提出了基于电容电流反馈的有源阻尼方法[7]，该方法具有谐振抑制效果优良、实现方式简单以及易于技术人员掌握等优势，在实际工程中受到了广泛应用[8-11]。但在考虑控制延时的情况下，采用电容电流反馈有源阻尼方法可能会导致系统不稳定。文献[12]首先指出控制环路中的控制延时将严重影响有源阻尼方法的阻尼效果，导致有源阻尼的等效虚拟电阻的正负性受频率的约束，且分界频率为1/6倍采样频率。文献[13]指出在LCL谐振频率高于分界频率的场合中，电网阻抗的变化可能会使谐振频率接近甚至跨越分界频率，此时系统容易发生失稳现象。由此可见，如何切实有效地解决控制延时引起的系统不稳定问题就显得尤为重要。

目前而言，国内外学者针对上述问题已作出了一定的研究。文献[14]提出了基于模型预测的延时补偿方法，但该类方法的有效性是建立在精准模型的基础上，在实际应用中，模型的精准度往往会由于电气参数波动而降低，因此该方法的实现效果仍然欠佳。文献[15]在前向通路中加入了滞后补偿环节，从而通过改变环路增益的穿越情况来解决该问题，但该类方法会减少系统的相位裕度，不利于系统的动态响应能力。文献[16-17]在电容电流反馈通路中加入了超前补偿环节，延时补偿效果良好，但补偿环节的高通特性会放大采样过程中的开关噪声，影响了系统的控制性能。

为了更好地解决控制延时引起的系统不稳定问题，本文提出了一种基于SOGI的LCL型并网逆变器延时补偿方法，首先分析了补偿方法的实现原理，之后给出了SOGI参数的设计标准。通过理论分析后发现，所提补偿方法可在不引入过量开关噪声的情况下有效提升系统对电网阻抗的鲁棒性，使得并网逆变器在电网阻抗变化时始终保持稳定。最后搭建了输出功率为4.5 kW的实验样机，验证了补偿方法的有效性与正确性。

1 建立LCL型并网逆变器的数学模型

单相LCL型并网逆变器的系统拓扑结构如图1所示，主要由光伏发电端、单相全桥并网逆变器以及LCL滤波器构成，该系统能完成交直流的快速转变与公共电网的功率馈入。

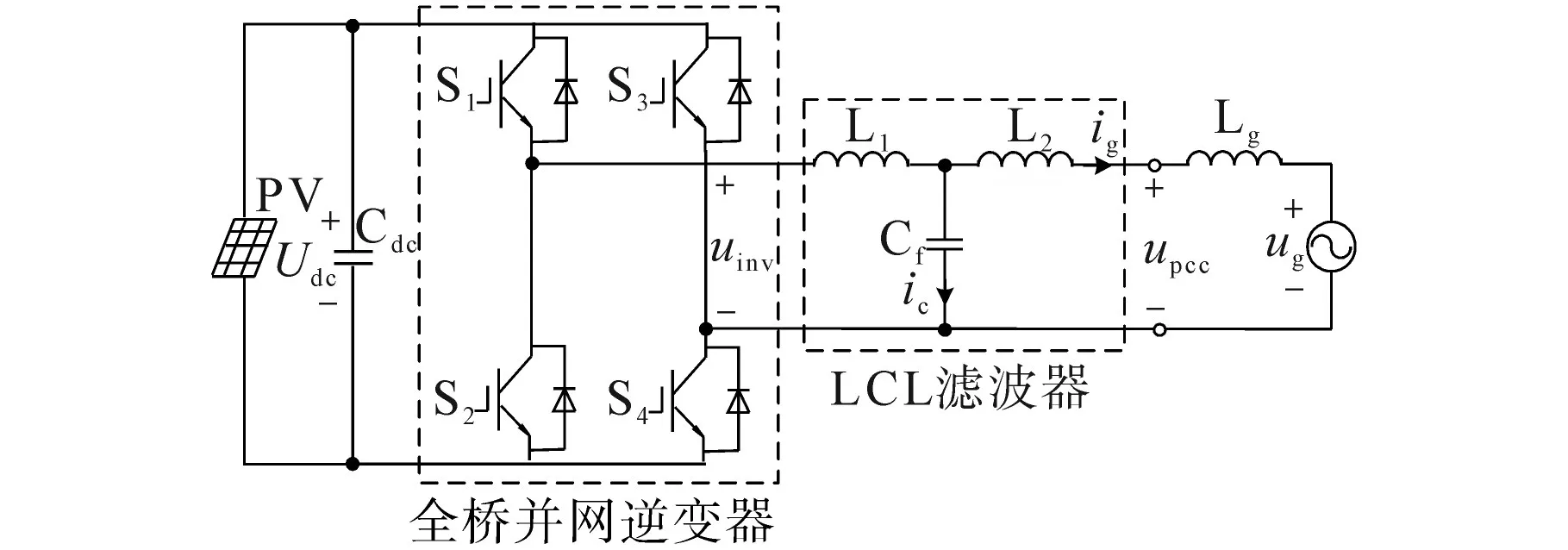
图1 单相LCL型并网逆变器的系统拓扑结构Fig.1 System topology of single-phase LCL-type grid-connected inverter

图1中，Udc为光伏发电端产生的直流母线电压；Cdc为直流储能电容；uinv为输出电压；L1，Cf，L2分别为LCL滤波器的逆变器侧电感、滤波电容以及网侧电感；ig为网侧电流；ic为电容电流；ug为电网电压；upcc为并网点电压；电网阻抗Lg假设为纯感性。

在并网逆变器的电流控制环中，通常存在1.5个采样周期的控制延时[13]，将其记为Gd（s），由于Gd（s）为超越函数，不利于传递函数的求解与分析，因此可对其进行二阶pade近似[18]，表达式如下式所示：

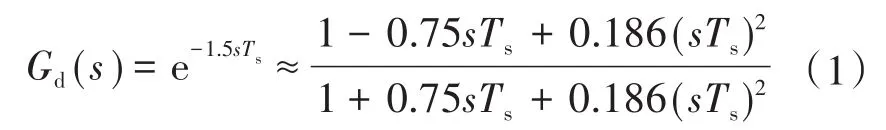
式中：Ts为采样周期。

图2为并网逆变器采用电容电流反馈有源阻尼方法时的电流环控制框图，其中，H1为有源阻尼反馈系数；Kpwm为增益系数；ug（s）为电网电压扰动；Gi（s）为经典的准比例谐振控制器，可实现网侧电流ig（s）的无静差跟踪，表达式如下式所示：

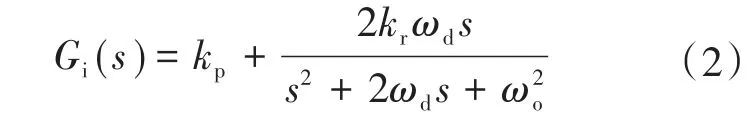
式中：kp为比例系数；kr为谐振系数；ωd为控制器阻尼系数；ωo为基波角频率。

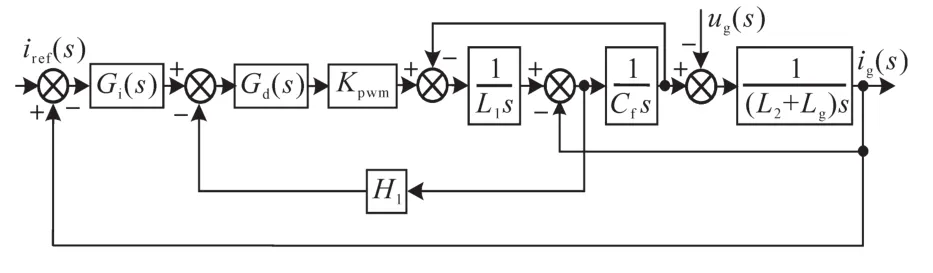
图2 采用电容电流反馈有源阻尼方法的电流环控制框图Fig.2 Current-loop control block diagram with capacitor-current feedback active damping method

由图2可得到系统的开环传递函数，如下式所示：

其中

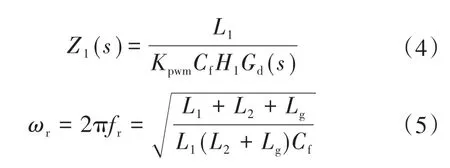
式中：Z1（s）为有源阻尼的等效虚拟阻抗；ωr为LCL谐振角频率；fr为LCL谐振频率。

Z1可进一步表示为虚拟电阻R1与虚拟电抗X1并联的形式[15]，如图3所示。

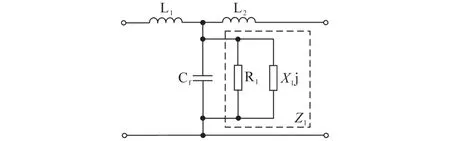
图3 虚拟阻抗Z1的等效电路图Fig.3 Equivalent circuit diagram of virtual impedance Z1

图3中，R1与X1的表达式如下所示：

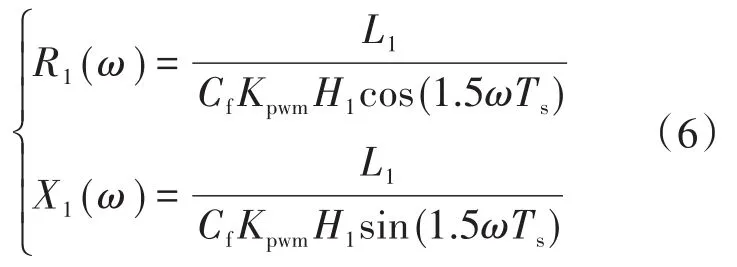
其中，由Gd（s）引入的cos（1.5ωTs），sin（1.5ωTs）函数将使得R1的正负性和X1的容感性受频率的影响[19]。设置fs为采样频率，若fr＞fs/6，环路增益将在fs/6和fr处穿越-180°，其幅值裕度需满足相应的条件才可使系统稳定，但在Lg变化的情况下，Lg的增大将使fr不断下降，若fr过于接近fs/6，环路增益的幅值裕度可能会不满足相应的稳定条件，进而导致系统失稳[20]。

目前，已有较多文献对上述问题进行了详细的理论分析，因此本文对此不再作重复叙述。

2 基于SOGI的LCL型并网逆变器延时补偿方法

为解决控制延时引起的系统不稳定问题，其核心思路在于减小电容电流反馈通路中控制延时造成的相位滞后，故本文在电容电流反馈通路中加入了SOGI，利用SOGI的相位超前特性来抵消控制延时造成的相位滞后，SOGI的表达式如下式所示：

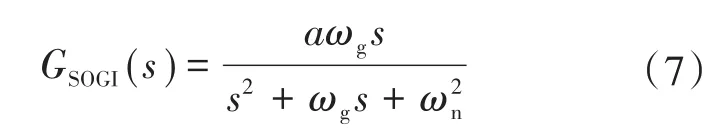
式中：ωg为SOGI的谐振系数；ωn为带通信号的角频率；a为幅值调整系数。

采用补偿方法后的电流环控制框图如图4所示。

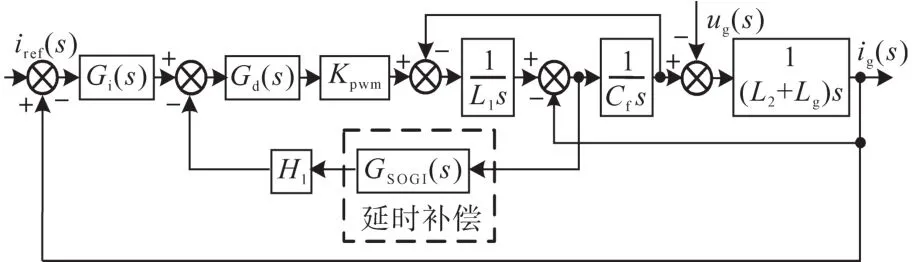
图4 采用补偿方法后的电流环控制框图Fig.4 Current-loop control block diagram with compensation method

由图4可得到采用补偿方法后的环路增益表达式：

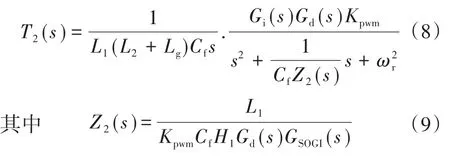
式中：Z2（s）为采用补偿方法后的有源阻尼等效虚拟阻抗。

2.1 延时补偿原理

令s=ωj，并对式（7）进行化简整理后可得：

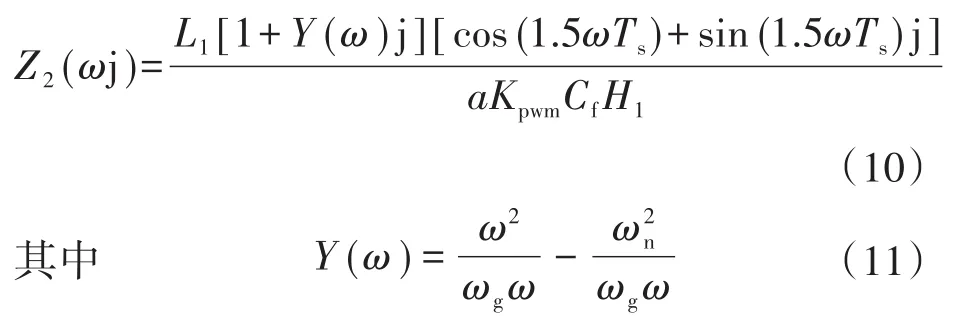
对式（10）作进一步化简整理后，可得到如下等式：

式中：θ为GSOGI引入的相位补偿量。

Z2同样可表示为R2和X2并联的形式，对式（12）作进一步处理，R2与X2的表达式如下所示：

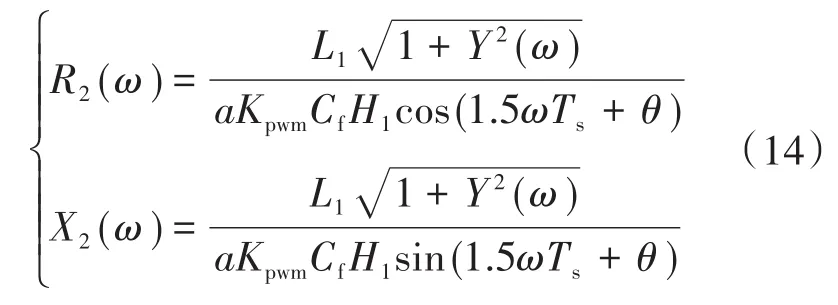
由式（14）中R2的表达式可以看出，θ的正负性将改变R2的正阻性范围，当θ＜0时正阻性范围被扩大，而当θ＞0时正阻性范围被缩小，而θ的正负性将取决于Y（ω）中ωn的大小，通过观察式（11）的表达式后，可以得出以下关系：

由式（15）所示的关系式可知，为了在奈奎斯特频率fs/2内能实现延时的补偿，ωn的取值应当越大越好，但由式（13）中θ的表达式可知，SOGI提供的相位补偿量θ的最大值不超过-π/2。因此，本文提出的基于SOGI的延时补偿方法最高可将R2的正负分界频率fR2提升到fs/3左右，如图5所示。

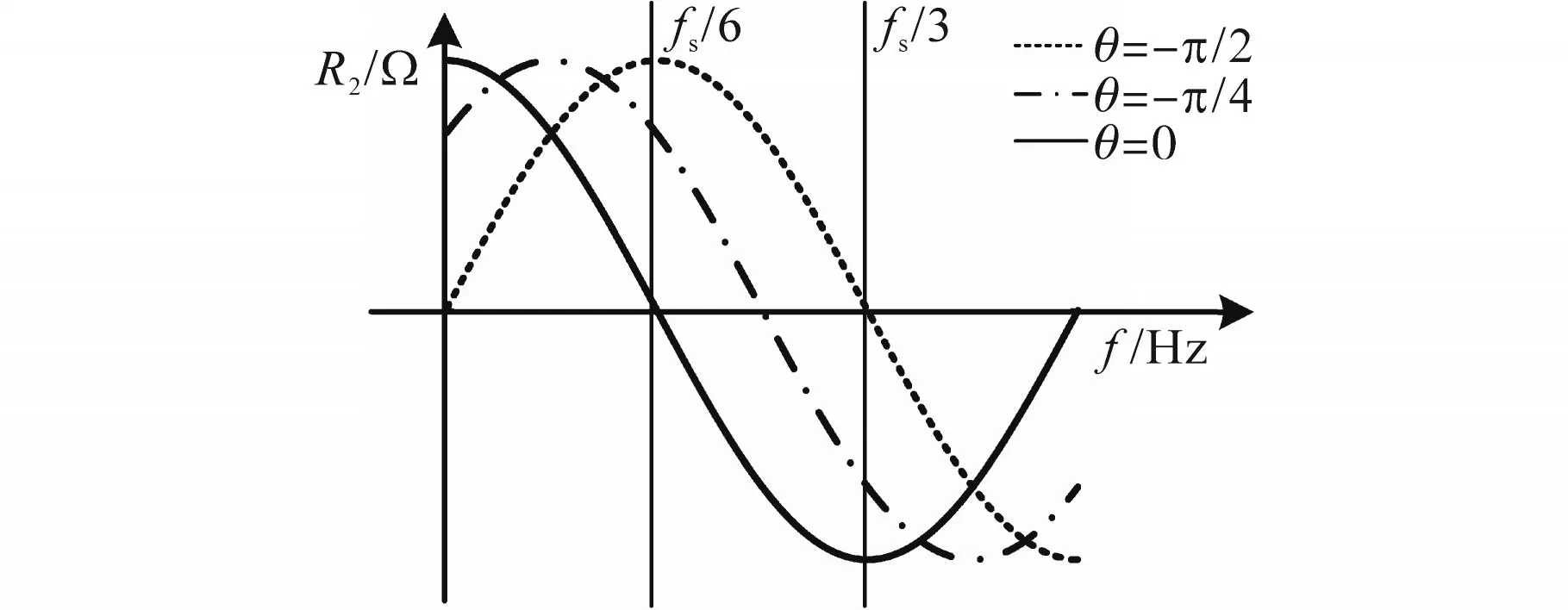
图5 θ不同时fR2的变化情况Fig.5 Variation of fR2with different θ

2.2 SOGI参数设计

根据上节的理论分析可知，为了使SOGI在全频段内能实现延时补偿，其带通信号的角频率ωn应设置为πfs，同时令s=ωj并代入式（7）后可得到SOGI的幅频表达式和相频表达式：

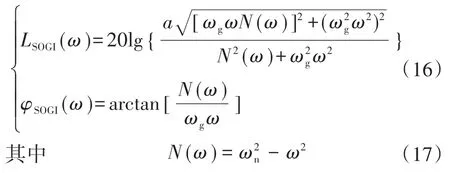
图6为ωg和a变化时SOGI的伯德图，实线代表的SOGI参数为a=1，ωg=2 000 π；断线部分代表ωg不变但a变化时的SOGI幅相频特性；点线部分代表a不变但ωg变化时的SOGI幅相频特性。通过图6中的点线部分不难发现，ωg越小，则SOGI的延时补偿效果越好，但fs/2范围内的幅值衰减越严重，从而等效地减小了电容电流反馈通路中的幅值增益，不利于系统拥有良好的幅值裕度。而通过图6中的断线部分不难发现，a的增大可以有效改善中高频段的幅值衰减状况且不影响SOGI的延时补偿效果，但会放大fs/2处开关噪声的幅值。因此，对于SOGI中a和ωg的取值需要进行折中考虑。

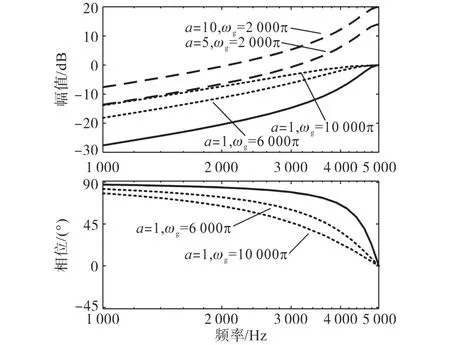
图6 ωg和a变化时SOGI的伯德图Fig.6 Bode diagram of SOGI when ωgand a change

由图6可知，增大ωg能减小SOGI的幅值衰减状况，但这也会牺牲SOGI的延时补偿能力，因此为了尽量保证SOGI拥有最好的延时补偿效果，可对参数a进行适当的调整，从而缓解SOGI的幅值衰减状况。

考虑到引入过量的开关噪声将严重影响系统的控制性能，因此需对a的取值进行约束。图7给出a增大时fs/2处开关噪声的幅值放大情况，一般情况下，fs/2处的噪声幅值不能超过10 dB[13]，进而可得a的取值范围，如下式所示，对应图7中的阴影部分：

由式（18）整理后可进一步得出a的取值范围：

根据上文的分析，为了最大程度保证SOGI的延时补偿能力，参数a可取式（19）中的最大值。

图7 参数a与fs/2处噪声幅值的函数关系Fig.7 Function relationship between parameter a and noise amplitude at fs/2

另一方面，为了保证SOGI的引入不影响有源阻尼对LCL谐振峰的抑制效果，电容电流反馈通路在ωr处的增益系数必须保持不变，因此，ωg的选取需满足以下等式：

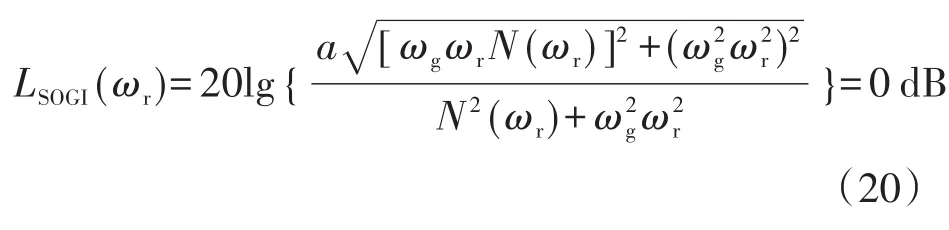
将式（20）展开后可得ωg的表达式：

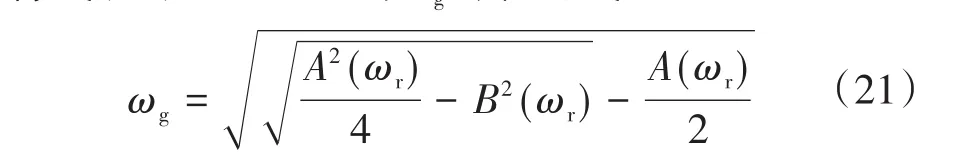
其中

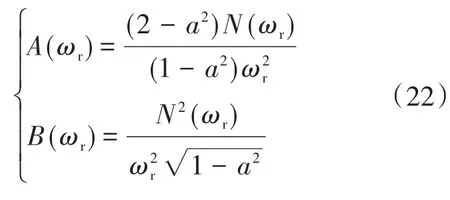
将式（5）代入式（21），可以得到ωg与fr之间的函数关系，如图8中的实线部分所示。同时根据式（14）中R2的表达式，可以得到正负分界频率fR2与变量ωg相关的表达式，如下式所示：

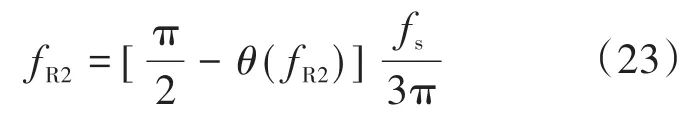
其中

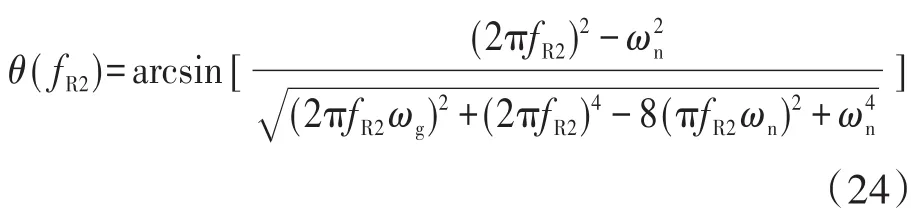
联立式（5）、式（21）～式（23）可以得到fR2与fr的函数关系，如图8中的虚线部分所示。

图8 fr与fR2，fr与ωg的函数关系Fig.8 Functional relationships between frand fR2 ，frand ωg

由图8可以发现，随着fr的增加，SOGI的谐振系数ωg需作出相应的调整才可满足式（20）所示的等式，并且随着ωg的变化，SOGI的延时补偿效果也会发生变化，使得正负分界频率fR2在（fs/4，fs/3）的范围内波动。

综上所述，在fr＞fs/6的情况下，基于SOGI的延时补偿方法至少可将fR2扩大至fs/4，从而提高了并网逆变器对电网阻抗的鲁棒性。

2.3 系统稳定性分析

根据文献[19]中并网逆变器的参数设计方法可设计出动静态性能优良的并网逆变器系统，其控制参数如下所示：逆变器侧电感L1=1.3 mH；网侧电感L2=0.75 mH；滤波电容Cf=9 μF；采样频率fs=10 kHz；开关频率fsw=10 kHz；载波幅值Utri=1 V；等效增益Kpwm=380；电容电流反馈系数H1=0.01；比例增益kp=0.026；谐振系数kr=2；直流侧电压Udc=380 V；电网电压ug（有效值）=220 V。参照所设置的控制参数以及2.2节中SOGI参数的设计方法，可得出相应的SOGI参数的值：a=3.16，ωg=5 000π，ωn=fs/2=5 000 Hz。进而得出正负分界频率fR2≈0.29fs。

根据图4，利用z域传递函数的推导方法可得出采用补偿方法后环路增益在z域下的表达式：

其中

式中：GSOGI（z）为SOGI在z域中的表达式，可采用中高频段内相似度较高的一阶保持法来对其进行离散化。

根据式（25）可以得出采用补偿方法后环路增益的伯德图，如图9所示。可以发现，提出的补偿方法可将正负分界频率由fs/6扩大至0.29fs，进而使得环路增益不存在右平面极点，解决了系统谐振频率接近fs/6时所导致的幅值裕度不足的问题。由此可见，当Lg在0～3.6 mH（对应短路比为10[21]）内变化时，提出的基于SOGI的延时补偿策略可使系统一直处于稳定状态，且具有充足的稳定裕度，大大提升了并网逆变器对电网阻抗的鲁棒性。

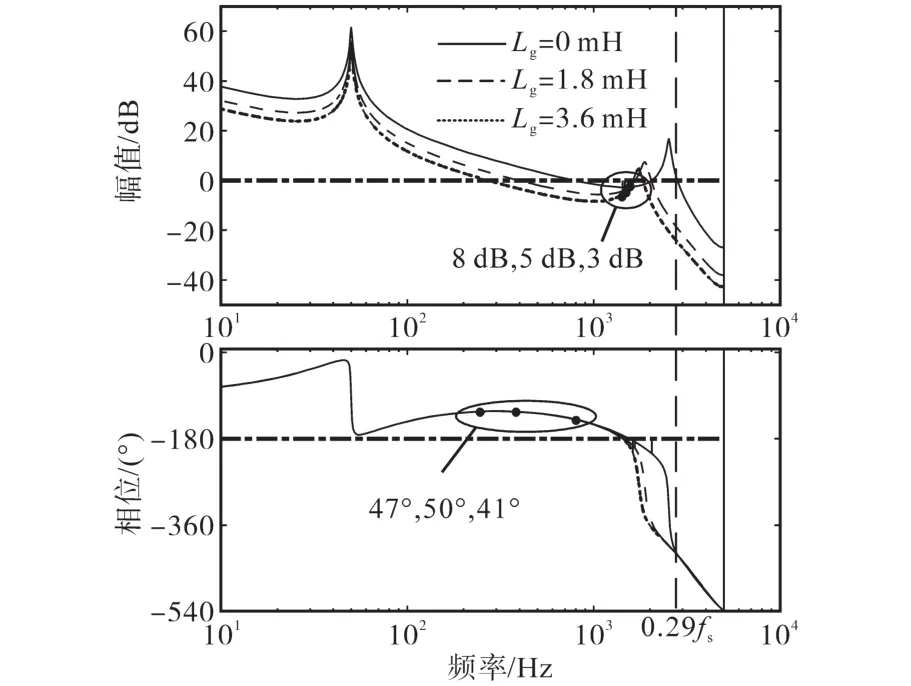
图9 采用补偿方法后环路增益的伯德图Fig.9 Bode diagram of loop gain with compensation method

3 实验验证

为验证补偿方法的有效性与正确性，在实验室中搭建了输出功率为4.5 kW的单相LCL型并网逆变器实验样机，实验样机的数字信号处理器采用TI公司的TMS320F28335芯片，公共电网采用可编程交流源Chroma 6460和串联电感的方式来模拟，实验参数与SOGI参数与2.3节相同，电网阻抗Lg变化范围为0～3.6 mH。

图10为Lg=0 mH时系统采用补偿方法前后的网侧电流稳态波形。由图10可以看出，当Lg=0 mH时系统采用补偿方法前后均能保持稳定，且电流波形质量良好，表明SOGI的引入基本不影响系统的稳定裕度，验证了2.2节中SOGI参数设计方法的正确性。

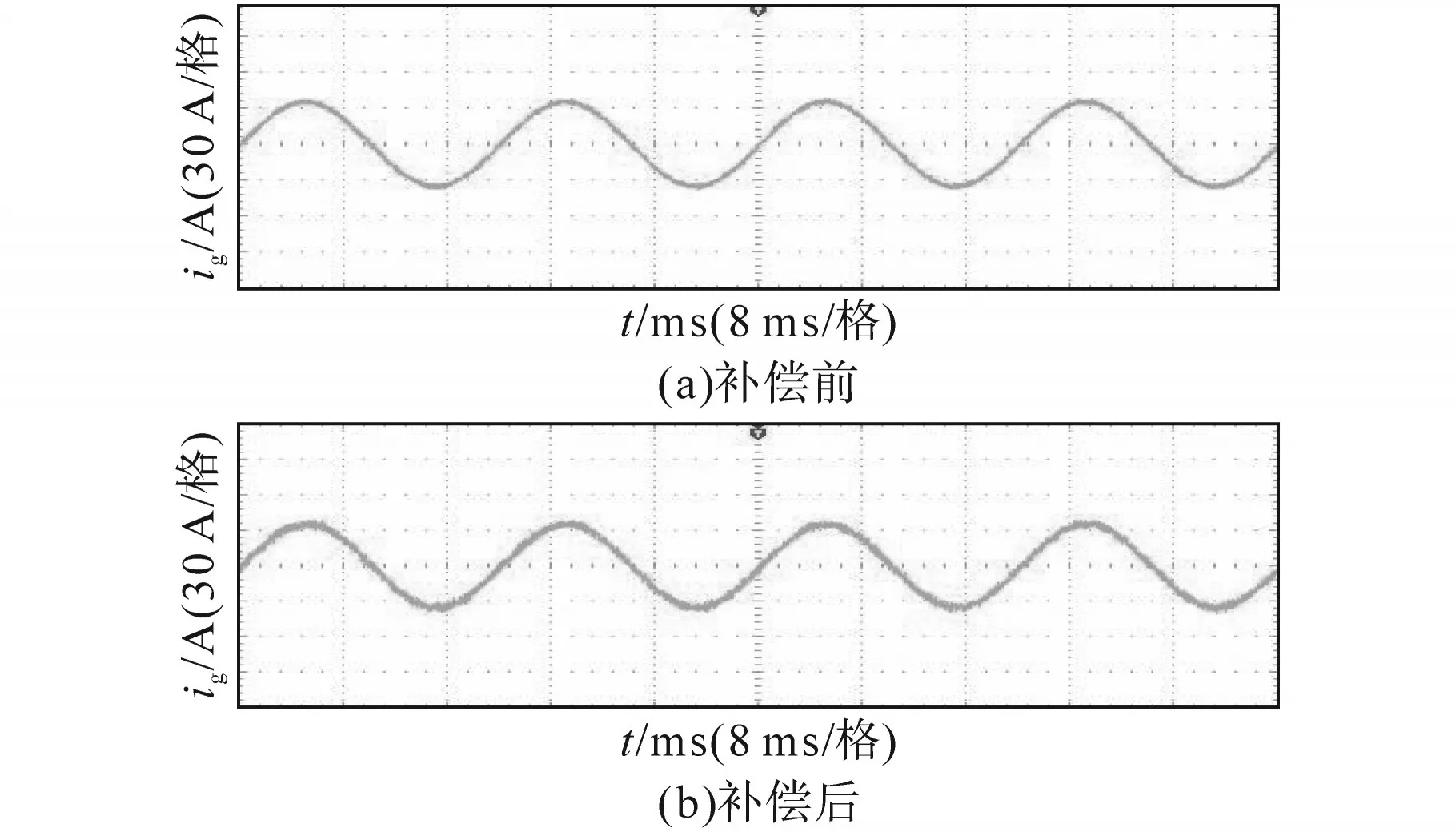
图10 Lg=0 mH时系统采用补偿方法前后的稳态波形Fig.10 Steady-state waveforms before and after using compensation method when Lg=0 mH

图11、图12分别为Lg=1.8 mH，3.6 mH时系统采用补偿方法前后的稳态波形。

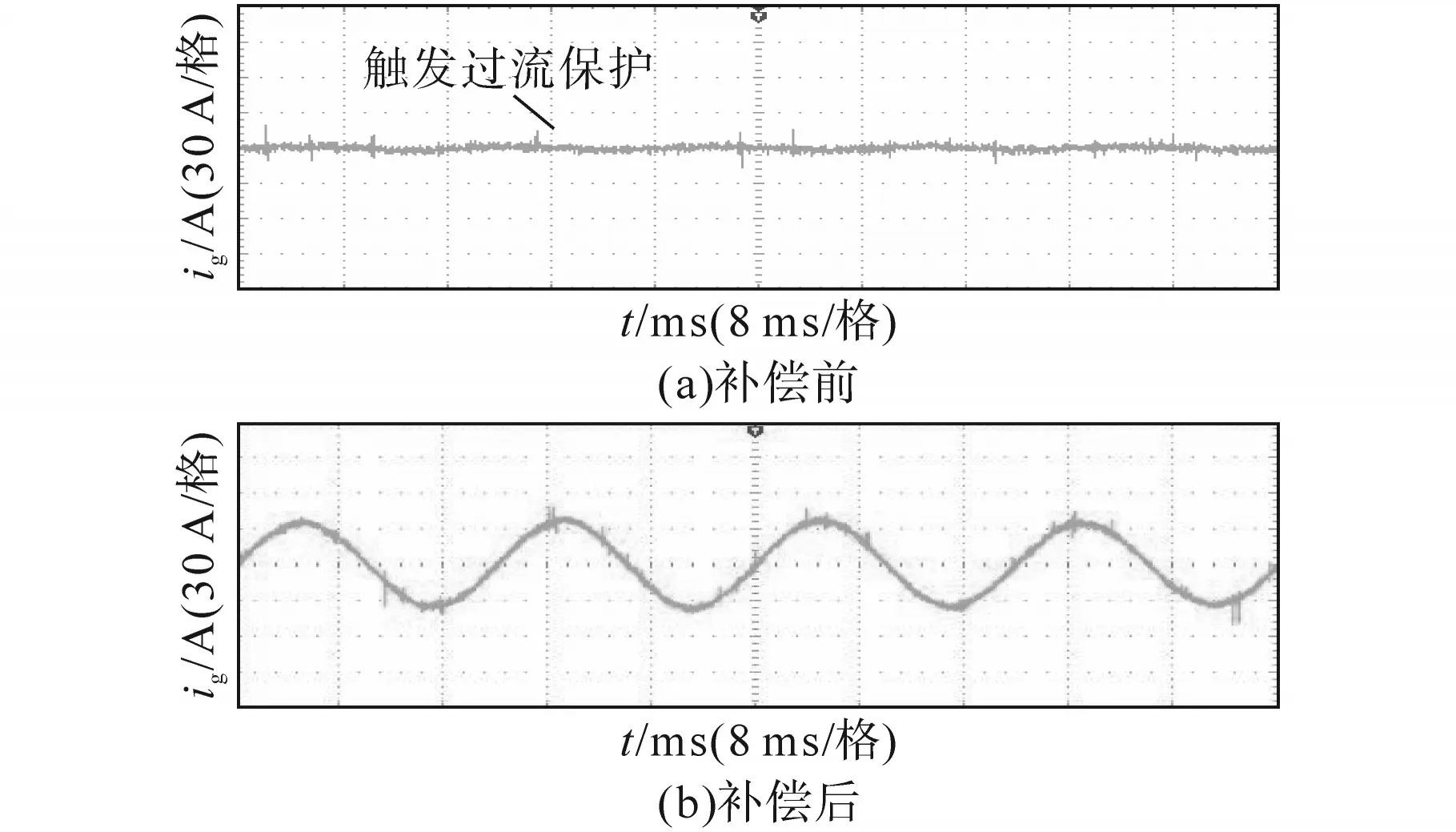
图11 Lg=1.8 mH时系统采用补偿方法前后的稳态波形Fig.11 Steady-state waveforms before and after using compensation method when Lg=1.8 mH

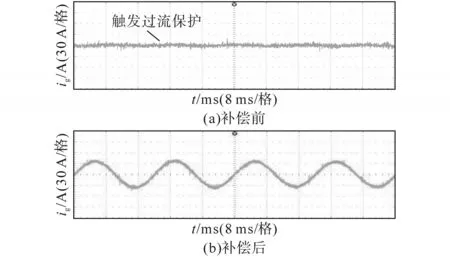
图12 Lg=3.6 mH时系统采用补偿方法前后的稳态波形Fig.12 Steady-state waveforms before and after using compensation method when Lg=3.6 mH

如图11a、图12a所示，当Lg=1.8 mH，3.6 mH时，系统在采用补偿方法前难以适应电网阻抗的变化，一旦开机并网，逆变器过电流保护机制立即被触发，系统始终无法正常工作。而由图11b、图12b可看出，系统在采用补偿方法后，网侧电流ig呈现较为标准的正弦波形态，系统始终处于稳定状态，表明补偿方法能有效补偿电容电流通路中的控制延时，从而使系统在电网阻抗变化时具备良好的稳定裕度，显著地提升了并网逆变器对电网阻抗的鲁棒性。

综上，实验结果与理论分析结果一致，验证了补偿方法的有效性。

4 结论

文章以采用电容电流反馈有源阻尼的LCL型并网逆变器为研究对象，详细分析了控制延时引起的系统不稳定问题，并针对该问题提出了有效的解决方法。

主要内容及结论如下：

1）控制延时将影响有源阻尼中虚拟电阻的阻性，若LCL谐振频率fr＞fs/6，在电网阻抗发生变化时系统容易发生不稳定现象。

2）为解决控制延时引起的系统不稳定问题，提出了基于SOGI的延时补偿方法，理论分析结果表明该方法可在不引入过量开关噪声的情况下大幅度提升等效虚拟电阻正负分界频率的大小，显著地增强了并网逆变器对电网阻抗的鲁棒性。

3）在实验室中搭建了实验样机，且实验结果与理论分析结果一致，即补偿方法能使并网逆变器在电网阻抗变化时稳定运行。