基于条件生成对抗网络的扇区复杂度评估

张魏宁，胡明华，杜婧涵，尹嘉男

（南京航空航天大学，民航学院，南京 211106）

0 引言

持续增长的空中交通需求驱动了航空运输业的蓬勃发展，与此同时，也伴随着空域拥挤、飞行冲突等问题的出现。为了维持飞机间适当的间隔，确保其安全、高效、有序地运行，空中交通管制员需要实时监视空域交通态势并向飞行员发布管制指令[1]。然而，当交通密度达到空域容量限制时，管制员处于较高的工作负荷状态，可能会导致操作错误进而引发不安全事件。扇区复杂度[2]，作为客观描述管制员监视和管理所负责扇区交通状况难度的指标，在一定程度上反应管制员所面临的管制压力。预先准确地评估扇区复杂度，一方面，有利于更好地进行交通流量管理，通过调节交通流量达到空域容需平衡；另一方面，能够作为动态空域配置的参考依据，通过重新规划管制扇区并合理分配有限的管制资源来平衡各管制员的工作负荷[3]。

针对扇区复杂度的评估问题，已有较多国内外学者进行研究。LAUDEMAN等[4]首次引入动态密度概念，将各种潜在影响因素，例如，交通流量、冲突扰动等进行线性组合。相比交通密度而言，动态密度与扇区复杂度的相关性更高，解释性更强。此外，为捕获各因素间存在的复杂非线性关系，GIANAZZA 等[5]利用神经网络模型学习各因素与扇区状态之间的联系。本质上，这些模型通常将复杂度评估问题转化为一般模式识别问题[6]，即以容易获得的雷达轨迹数据计算的各种影响因素作为输入，精准预测能够代表实际扇区复杂度的量化指标，例如，管制员身体活动、主观评分、扇区状态等。近年来，研究人员发现扇区复杂度评估模型的效果通常依赖于数量充足、标记可靠的数据集[7]。然而，获取这样的数据集往往需要领域专家积极参与并付出昂贵的时间代价，例如，空中交通管制员实时地反馈对空域运行态势和工作负荷的主观感受等。因此，在样本量较小的数据集上建立评估模型更具有实际意义。针对该问题，ZHU等[8]在因子噪声和独立性分析的指导下，生成多个因子子集，构建集成学习模型预测扇区复杂度。CAO 等[9]提出基于知识转移的扇区复杂度评价框架，通过挖掘并融合目标扇区和其他非目标扇区中隐藏的知识，增强小样本环境下扇区复杂度的预测性能。在多个扇区下进行的实验验证了该框架的优越性。

本文以少量、有标记的数据集为基础，提出基于条件生成对抗网络的扇区复杂度评估框架，利用条件生成对抗网络生成包含不同复杂度等级的有监督样本，丰富已有数据集的多样性，以此缓解数据集中存在的样本量较小和类别不平衡问题。在中国中南区域扇区的真实运行数据下，应用多种扇区复杂度评估模型进行实例验证。

1 模型介绍

1.1 扇区复杂度评估框架

首先，利用雷达轨迹数据计算的潜在影响因素和相应的主观复杂度等级得到待评估扇区原始数据集，并将其划分为训练集和测试集两部分，根据训练数据集学习条件生成对抗网络；然后，利用该网络生成指定标号的样本得到生成数据集，并使用结合训练数据集和生成数据集的增广数据集训练扇区复杂度评估模型；最后，基于训练好的评估模型预测待评估扇区测试数据集的复杂度等级。基于条件生成对抗网络的扇区复杂度评估框架如图1所示。

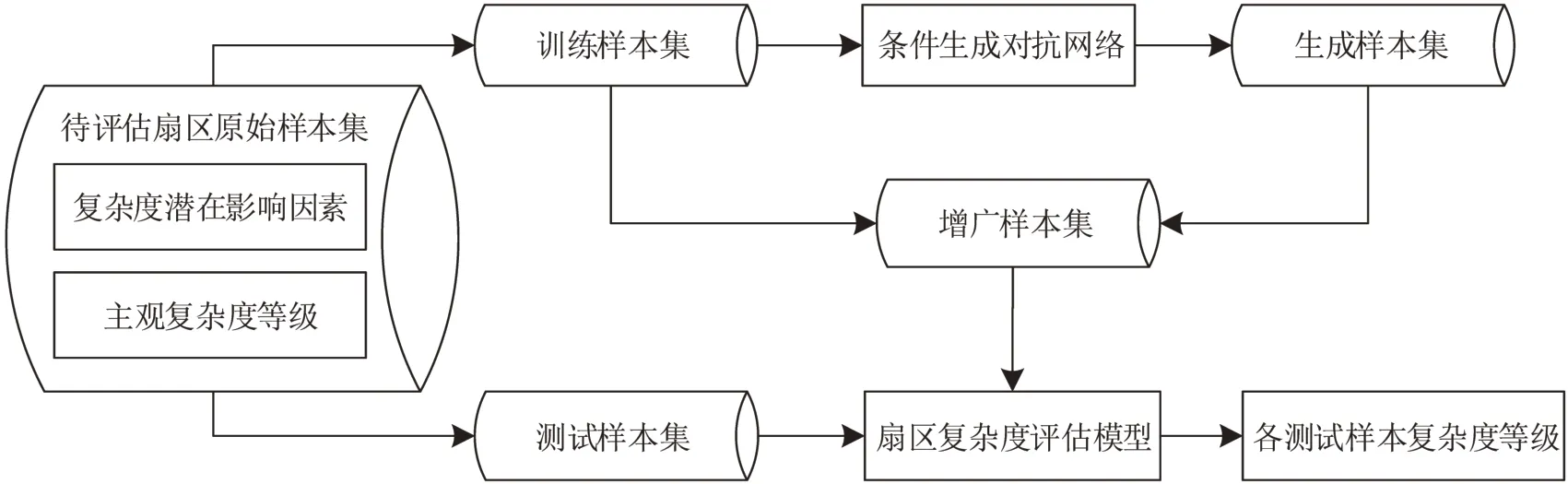
图1 基于条件生成对抗网络的扇区复杂度评估框架Fig.1 Sector complexity evaluation framework based on conditional generative adversarial network

1.2 复杂度数据集构建

扇区复杂度往往受多种因素的共同影响，基于已有文献，本文从交通流量、航空器性能和潜在冲突3个维度构建复杂度指标体系。其中，交通流量类指标直接反映扇区当下及未来一段时间内航空器的分布情况，通常作为空管系统实际应用中描述空域交通态势的基础指标；航空器性能类指标主要包括与航空器运行相关的速度参数，体现运行过程中产生的波动性；潜在冲突类指标从不同角度量化航空器间的碰撞风险，例如，分离、汇聚敏感度指标描述了航空器速度、航向变化对相对距离带来的影响，是引起管制员工作负荷激增的重要因素。扇区复杂度指标体系如表1所示。

表1 扇区复杂度指标体系Table 1 Sector complexity index system

本文采集了中国中南区域某扇区在2019年12月1～7日的真实雷达数据，每个数据包含：航班号、时间戳、位置(经度、纬度和高度)、速度等信息。根据该数据源，以1 min 为基本时间粒度计算了表1中的23个复杂度指标(潜在冲突类指标的计算方法参考文献[5])，并选取部分样本给管制专家进行复杂度等级的标定，包括：低、中、高3个等级。最终，整个数据集由1060条有标号的扇区复杂度样本组成，其中复杂度等级从低到高的样本数量分别为：455、436 和169。可以看出，由于该空域实际的运行情况，在这些已标记复杂度等级的数据中，复杂度等级高的样本数量远少于等级低的样本数量，这种类别不平衡现象进一步增加了复杂度评估模型的评估难度。

1.3 有标记样本生成

为缓解数据集小样本量和类别不平衡现象给复杂度评估模型精度带来的影响，需要学习不同复杂度等级下各指标的潜在分布规律，进而生成多样化的有标记样本扩增数据集。

生成对抗网络(Generative Adversarial Networks, GAN)是利用对抗式的学习过程估计生成模型的框架[10]，被广泛应用在图像、视频、文本等生成任务中。GAN 由判别器和生成器组成，生成器根据随机噪声生成样本，目标在于生成尽可能符合真实样本分布的样本；判别器用于推测输入样本是真实样本还是生成样本，目标是对样本来源进行准确地预测。整个框架统一的优化目标为

式中：E为数学期望；G和D分别为构成生成器和判别器的神经网络或深度模型的参数；pdata（x）和pz（z）分别为真实样本x和随机噪声z的分布；G（z）为基于随机噪声z生成的样本；D（x）为样本x属于真实样本的概率。通过基于随机梯度下降法的迭代优化对G和D进行交替训练，使得生成器可以学习训练样本的真实生成分布，进而从该分布中生成新的样本。GAN 和CGAN 的模型结构如图2所示。

由于GAN 模型只能从随机噪声中生成样本，限制了其使用价值。近年来，不少学者通过对生成器的输入提供额外信息生成更多样化、高质量的样本，这类GAN 模型被称为条件生成对抗网络(Conditional Generative Adversarial Networks,CGAN)[11]。以样本类别标号作为辅助信息为例，CGAN的模型结构如图2(b)所示。相比GAN模型，CGAN 的生成器在类别标号与随机噪声的共同作用下，生成指定类别的样本；其判别器不仅推测输入样本的来源，还要预测样本所属的类别。整个框架的优化目标分为样本正确来源的似然Ls和样本正确类别的似然Lc，即

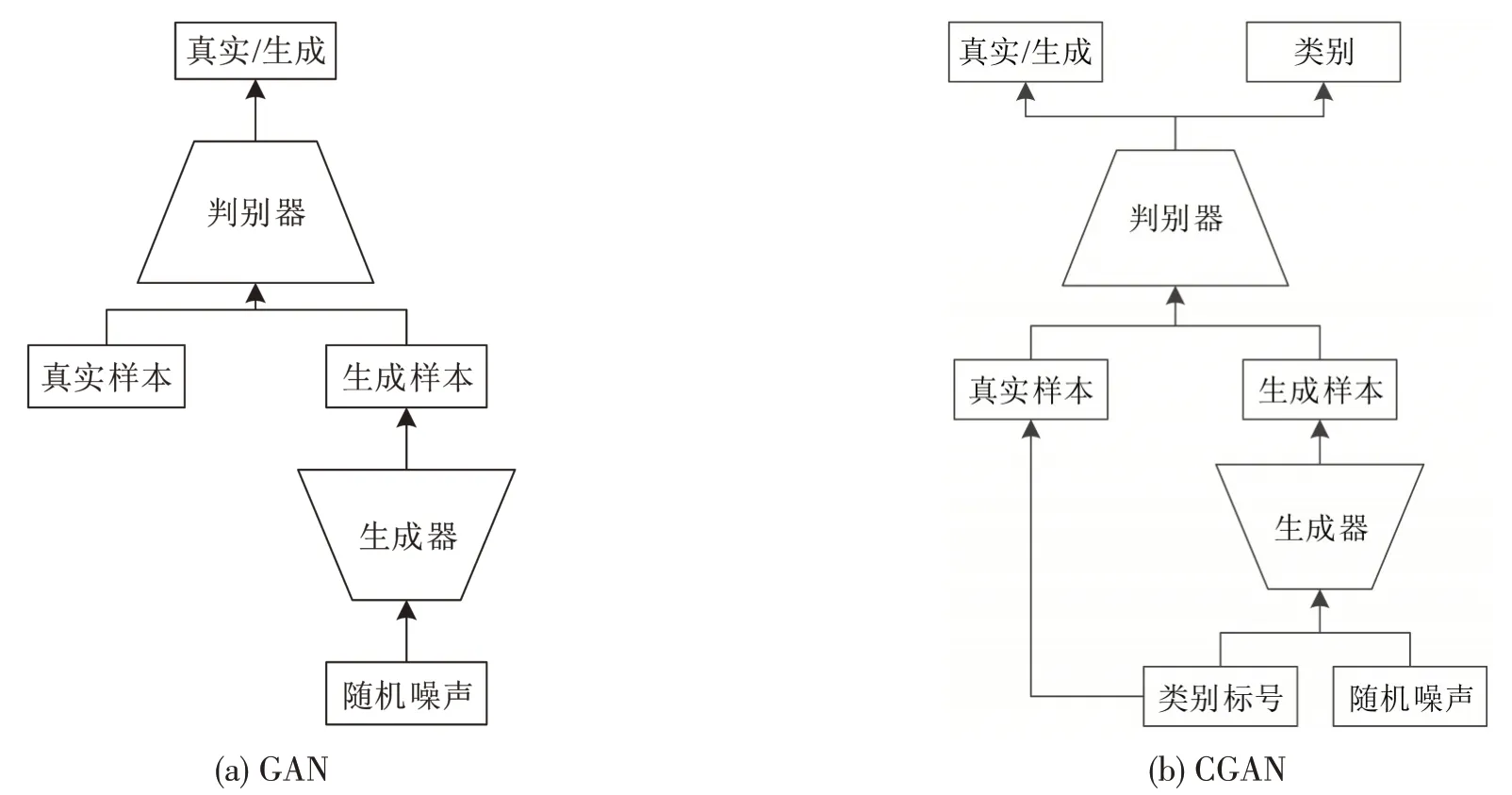
图2 GAN和CGAN的模型结构Fig.2 Model structure of GAN and CGAN

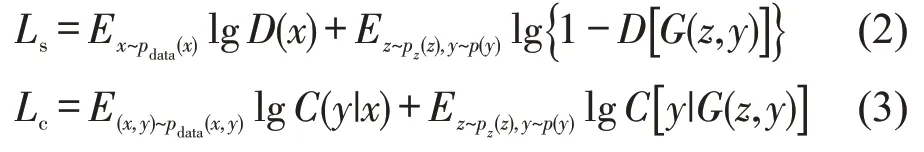
式中：p（y）为生成样本的类别标号的分布；pdata（x,y）为真实样本x及其类别标号y的联合分布；G（z,y）为基于随机噪声z和指定类别标号y生成的样本；C（y|x）为样本x属于类别标号y的概率。在模型训练的过程中，判别器的目标为最大化Ls+Lc，而生成器的目标为最小化Ls-Lc。由于引入了类别标号的先验知识和Lc的优化目标，CGAN 生成样本的多样性和稳定性往往优于GAN。因此，本文选取CGAN作为生成样本的基本模型，在已有扇区复杂度数据集上，生成更丰富的样本，进而增强后续扇区复杂度评估模型的精度。扇区复杂度有标记样本生成算法如表2所示。CGAN 模型的训练过程详细内容见参考文献[11]。

表2 基于CGAN模型的扇区复杂度有标记样本生成算法Table 2 Algorithm for generating labeled samples of sector complexity based on CGAN model

1.4 扇区复杂度评估

将扇区复杂度评估问题视为机器学习中的有监督分类任务。利用管制专家对扇区样本复杂度等级的标定结果作为监督信息，分别基于逻辑回归、支持向量机和随机森林这3种经典的分类算法建立扇区复杂度评估模型。其中，逻辑回归(Logistic Regression, LR)模型是经典的分类方法，通过最大化数据集对数似然来估计模型参数。由于该模型属于线性分类方法，因此，将其视为基线模型；支持向量机(Support Vector Machines, SVM)模型则学习能够正确划分数据集类别的超平面，可以借助核函数解决非线性分类问题；随机森林(Random Forest, RF)模型是集成学习的代表性方法，在有差异性的数据子集中训练多个基分类器，并根据各个分类器的预测情况利用简单投票法给出最终的分类结果。

为了验证各模型的评估性能以及生成样本对复杂度评估结果的影响，设置多种配置下的训练集。如表3所示，R_L、R_M、R_H 分别表示低、中、高等级的真实训练集，F_L、F_M、F_H 分别表示与R_L、R_M、R_H 样本数量相同的低、中、高等级的生成样本集。其中，配置1～4 针对类别不平衡问题；配置1、5、6、7、8、9针对小样本问题。为保持数据规模一致性，配置8、9分别表示重复相同的真实训练集2次、3次。

表3 训练集的不同配置Table 3 Different configuration of training set

此外，为了对比不同实验配置下分类模型的效果，使用Micro-average F1-score (Micro-F1)和Macro-average F1-score (Macro-F1)两种常见的评价指标。作为F1-score 评价指标在多分类问题下的拓展，Macro-F1根据每一类的精确率和召回率计算相应类别F1-score，然后求算数平均，即

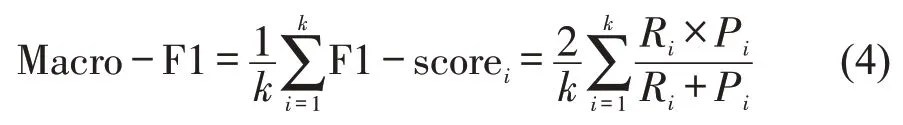
式中：k为类别数；Ri和Pi分别为第i类的召回率和精确率。Micro-F1 则首先计算所有类别总体的召回率和精确率，进而计算F1-score，即

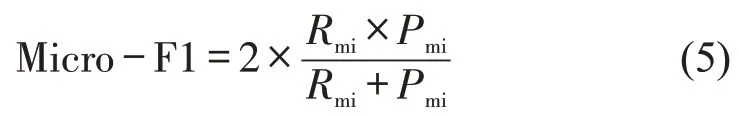
式中：Rmi和Pmi分别为总体的召回率和精确率，即

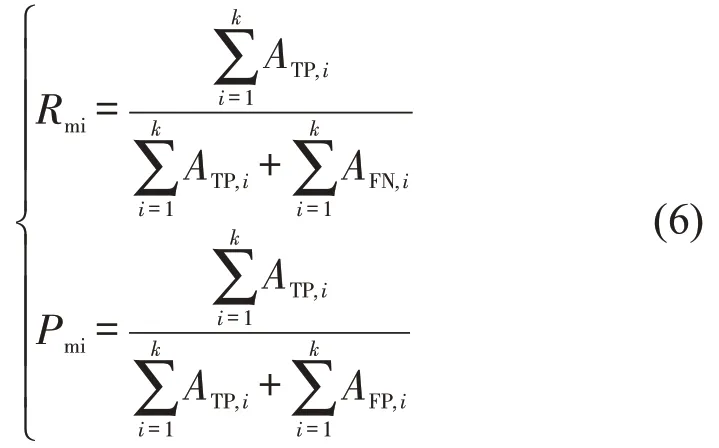
式中：ATP,i、AFP,i和AFN,i分别为第i类的真正类、假正类、假负类样本个数。从Micro-F1 和Macro-F1的计算方法可以看出，Micro-F1在多分类问题中等同于准确率，因此，更容易受到大样本类别的影响；Macro-F1由于平等地看待各个类别，更易受到小样本类别的影响。

2 实例分析

2.1 实验设置

本文基于深度学习框架Keras 2.0.8 实现CGAN模型。生成器的输入包含两部分，分别为随机噪声向量(77 维)和类别标号one-hot 向量(3 维)，两者拼接成完整的输入向量(80 维)。输出为特定类别下的生成样本(23 维)，其各维度分别对应表1中的各复杂度指标。中间隐藏层由全连接层和ReLU激活函数组成。判别器则以生成样本或真实样本作为输入，输出为给定样本属于真实样本的概率和属于各类别的概率，中间部分的隐藏层由全连接层和LeakyReLU 激活函数组成。为缓解训练过程可能存在的过拟合和梯度弥散现象，引入Dropout 和Batch Normalization 机制。整个模型参数通过截断正态分布进行初始化，并利用Adam 优化器进行训练，学习率和批量大小分别设置为0.0002 和32，Batch Normalization 的动量设置为0.8，Dropout 的比率设置为0.1。此外，模型隐藏层个数及相应神经元数量分别根据最小重建误差准则[12]和本征维数估计[13]进行确定。CGAN模型结构如表4所示。

此外，基于机器学习库Scikit-learn 0.22.2 实现各种扇区复杂度评估模型。在训练集上利用10折交叉验证的方法，确定了各模型的最优超参数。对于SVM模型，选择径向基函数作为核函数，惩罚参数C设置为1.0；对于RF 模型，共集成了10 个深度为6 的决策树进行预测。整个数据集被随机打乱顺序并用70%的数据作为训练集，30%数据作为测试集。其中，训练集首先用于训练CGAN模型生成样本，进而与生成样本一起学习复杂度评估模型，测试集仅用于复杂度评估模型的性能验证。

2.2 条件生成对抗网络学习效果分析

基于CGAN 模型的具体实现，进行了1000 次的迭代训练，训练过程中判别器对样本来源的预测精度变化情况如图3所示。

由图3可知，在200次迭代之前，预测精度呈现波动状态。从200次迭代以后，预测精度随着迭代次数的增加而逐渐降低，最终稳定在50%左右。这一现象直接反映了判别器对任意给定样本无法区分是真实训练样本还是生成样本，也间接体现了生成器所学习的数据分布随着迭代次数的增加逐渐接近于真实训练数据的分布。

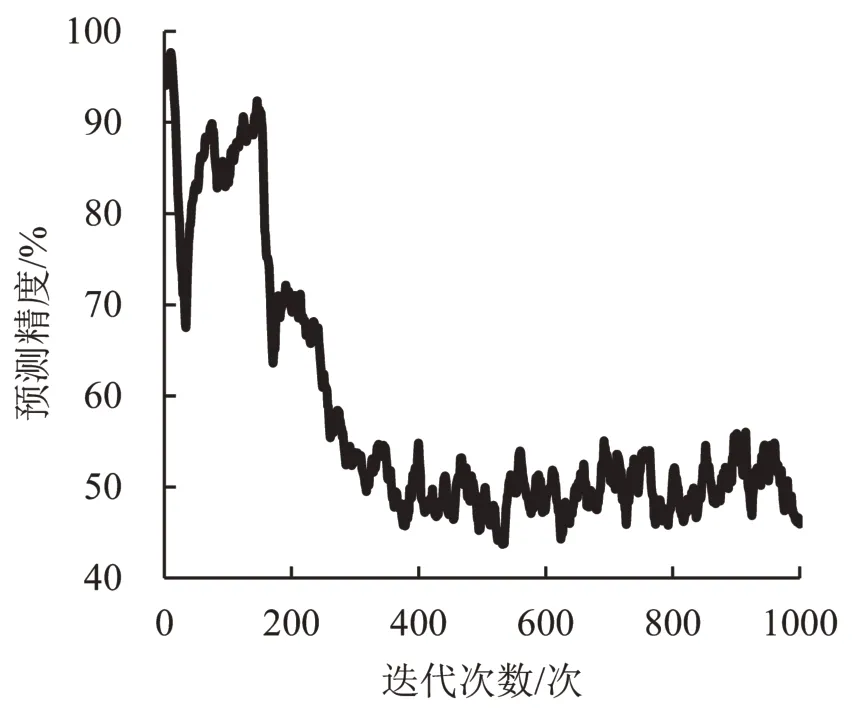
图3 样本来源的预测精度随迭代次数的变化Fig.3 Prediction accuracy of sample source varies with number of iterations

利用充分训练的CGAN模型，基于所提出的有标记样本生成算法，生成与训练集各类别样本数目相同的样本。由于各复杂度指标的取值范围不同，使用min-max 标准化方法将各指标映射到0～1 之间。为能够定量地对比生成样本与真实样本，分别统计了训练集和生成集各复杂度指标的均值和标准差，并可视化两者的相对误差。如图4所示。

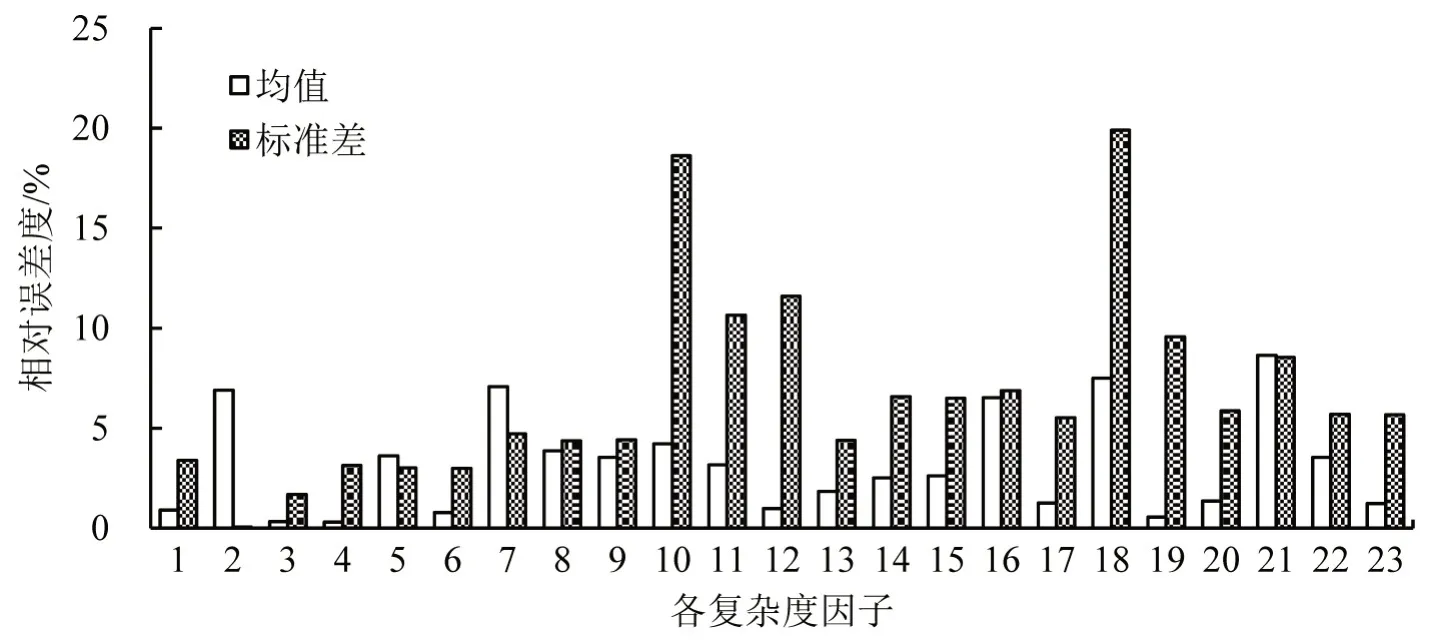
图4 生成集与训练集在均值和标准差上的相对误差Fig.4 Relative error between generating set and training set in mean and standard deviation

各复杂度指标在均值上的相对误差基本在5%以内，充分体现了CGAN模型学习到了真实数据的总体分布情况。此外，标准差的相对误差普遍较高，尤其是从第10个复杂度指标开始，即潜在冲突类指标。通过观察标准差的具体数值可以发现，该现象是由于真实样本集的潜在冲突类指标的标准差较小而生成集的标准差较大所导致。这种生成样本与真实样本之间的差异可以丰富样本的多样性，有效地增加样本数量，尤其是样本量较少的高复杂度样本，提高后续复杂度评估模型的鲁棒性和预测能力。

2.3 复杂度评估结果分析

为分析生成样本对扇区复杂度评估精度带来的影响，基于表2中7 种训练集配置分别学习了LR、SVM 和RF 模型。由于生成样本具有随机性，利用训练好的CGAN 模型生成30 组不同的样本集，依次评估每组样本集，得到Micro-F1 和Macro-F1 评价指标，并以平均值作为最终的性能结果。训练集配置为1～4下3种评估模型测试集的Macro-F1和Micro-F1影响如图5所示。

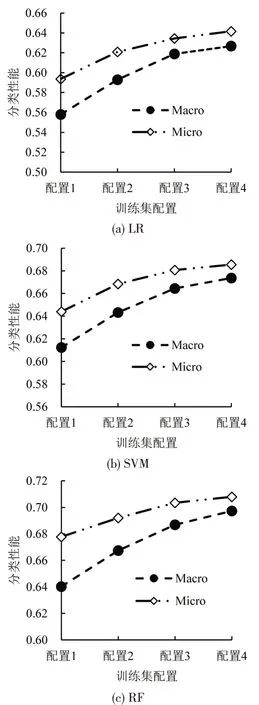
图5 不同训练集配置对3种评估模型的Macro-F1和Micro-F1影响Fig.5 Impact of different training set configurations on Macro-F1 and Micro-F1 of three evaluation models

由图5可知，同一训练集配置下，RF 模型的Macro-F1指标和Micro-F1指标最高，LR模型的指标最低，反映了不同模型的学习能力不同。随着生成的高复杂度样本的增多，各模型的指标均持续提高，表明了生成样本能够有效改善类别不平衡问题对性能的影响。进一步观察同一模型下指标的变化情况，Macro-F1 指标比Micro-F1 指标性能提升明显，这是由于Macro-F1 指标更易受小样本类别分类效果的影响，随着生成小样本类别样本数量的增加，其分类效果有明显的改善。

训练集配置为1、5、6、7、8、9 下3 种评估模型测试集的Macro-F1 和Micro-F1 分别如图6和图7所示。

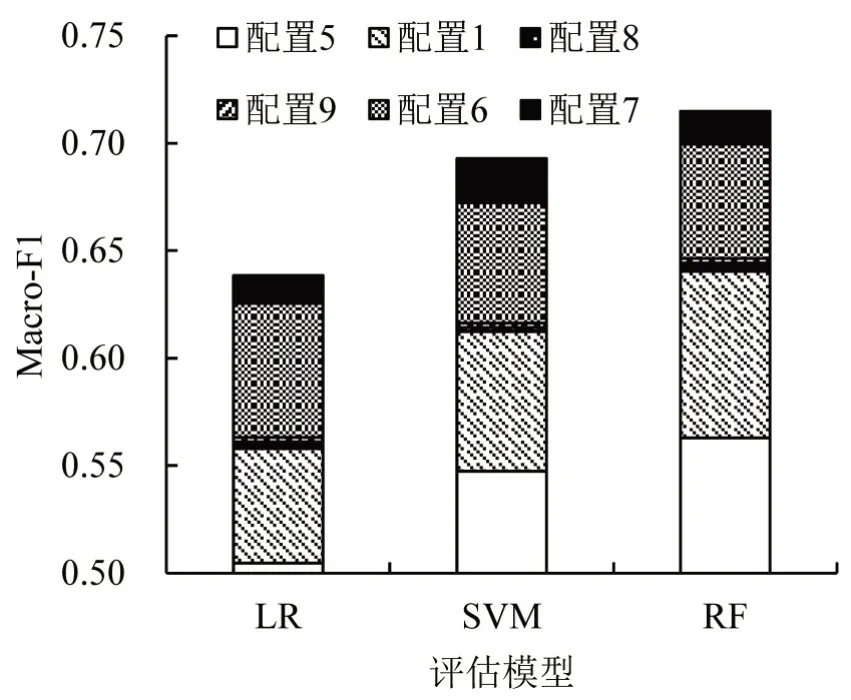
图6 不同训练集配置下3种评估模型在测试集下的Macro-F1Fig.6 Macro-F1 of three evaluation models in test set under different training sets

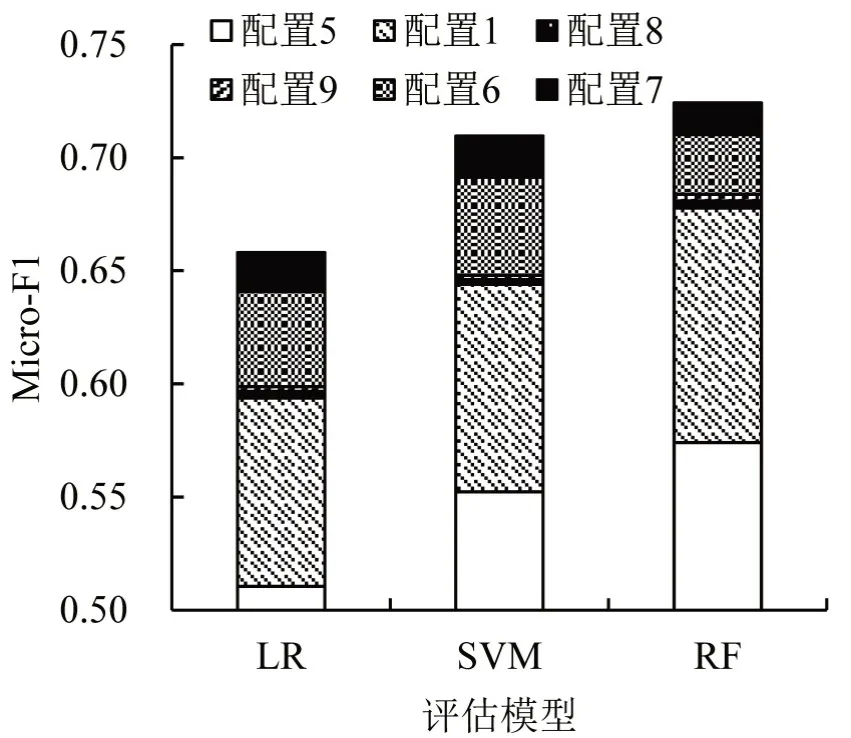
图7 不同训练集配置下3种评估模型在测试集下的Micro-F1Fig.7 Micro-F1 of three evaluation models in test set under different training sets

由图6和图7可以发现，两种评价指标取得了一致的变化情况。从配置1 到配置7，LR、SVM 和RF 模型的Macro-F1 指标分别增长了13.53%、12.53%和10.70%；Micro-F1 指标分别增长了10.01%、9.55%和5.98%。不论何种评估模型，配置5的性能远小于配置1。这体现了在各类样本数量相同的情况下，生成样本较真实样本在样本多样性上仍有一定的不足。此外，相较于配置1，配置6的性能有了明显的提高。这表明，通过混合生成样本得到的增广样本集能够增强复杂度指标的表达能力，缓解有标签样本量较少给模型预测带来的局限性。配置7在配置6的基础上进一步增加生成样本的数量，其性能仅有较小的提高。该现象反映了性能的提升不取决于生成样本的数量，而在于是否有效地丰富了样本的多样性。相较于配置6 与配置7，配置8与配置9本质上没有扩充有效训练样本的数量，因此，测试集性能几乎没有提升，也从侧面验证了生成样本多样性的重要性。

进一步给出不同配置条件下各评估模型总体的召回率和精确率，如表5所示。

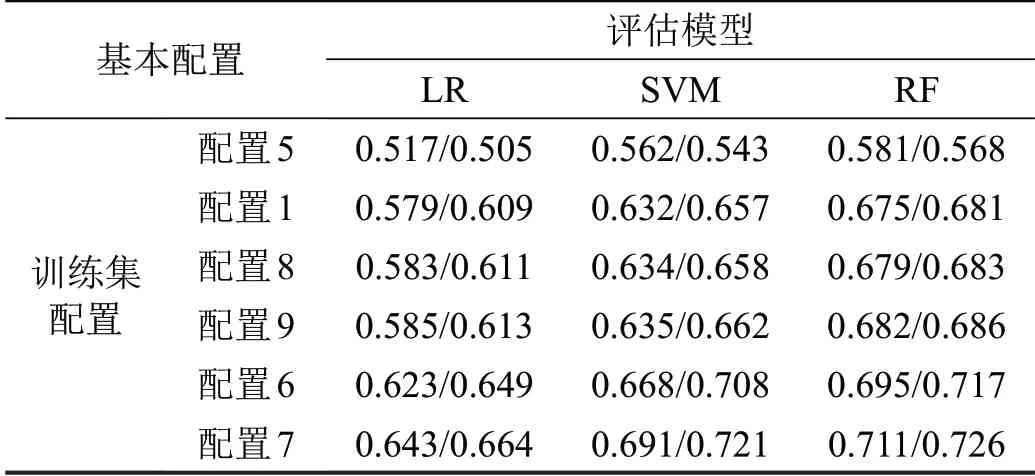
表5 测试集的总体召回率和精确率（Rmi Pmi）Table 5 Overall recall and precision of test set（Rmi Pmi）

由表5可知，配置5的总体召回率比精确率高；配置1、6、7、8、9 的总体召回率低于精确率。整体上看，召回率和精确率相差不大。

以上实验结果一致表明，生成样本能够有效提高小样本环境下复杂度评估模型的性能。

3 结论

本文的主要结论如下

(1)提出的基于条件生成对抗网络的扇区复杂度有标记样本生成算法的实验结果表明，生成样本的复杂度指标与真实样本在均值上的相对误差普遍小于5%，在标准差上的相对误差普遍大于5%。说明条件生成对抗网络能够有效地学习各复杂度指标的分布情况，与真实样本相比，具有一定的区分度。

(2)在扇区实际运行数据下，采用逻辑回归、支持向量机、随机森林算法验证了生成样本对扇区复杂度评估精度的有效性。对于Macro-F1 指标，评估精度分别增长了13.53%、12.53%和10.70%；对于Micro-F1 指标，评估精度分别增长了10.01%、9.55%和5.98%。表明生成样本能够很好地补充原始数据集，提高扇区复杂度的评估精度，为交通流量管理和管制负荷量化提供支持。