基于连续体近似法的特大城市公交系统规划研究

刘雪杰，荣朝和，欧阳彦峰，卡洛斯·F·达冈佐，朱家正，马腾腾

（1.北京交通大学，经济管理学院，北京 100044；2.北京交通发展研究院，北京 100073；3.伊利诺伊大学，土木与环境工程系，厄巴纳，伊利诺伊州 61820，美国；4.加利福尼亚大学，土木与环境工程系，伯克利，加利福尼亚州 94702，美国）

0 引言

从经济学的视角看，公交网络规划的目标是以最小的用户和运营商广义成本，满足出行需求。很多学者利用数学规划模型和数值解方法进行了大量研究，这些模型被用于解决特定地形条件下的公交网络类型和多种类型服务的整合，以及不同规模公交系统的车辆和司机调度等问题[1]。利用数学规划模型进行网络设计的方法，需要输入大量的原始数据，在非常大的尺度上准备这种数据(例如，人口分布等)往往需要通过空间和时间上的聚合，换取可操作性，但会影响数据的质量。反之，解决方案又严重依赖于复杂的启发式方法，这些方法需要大量的计算成本[2]。由于这些计算负担，在中等规模以上的城市案例中，即使使用最先进的离散模型公式和商业求解软件，也无法成功获得精确最优设计。而且，在有限的数值实验范围内，计算负担限制了可以现实考虑的“假设”方案和多情景设计方案。目前，还没有城市根据纯粹的离散网络优化模型设计公交网络。

为便于理解公交线网规划，学者们通过使用连续量作为输入和输出的连续体近似(Continuum Approximation，CA)模型简化计算。早期的工作始于对通勤巴士系统的讨论，大多数研究考察了典型的网络拓扑结构，例如，网格结构和轴辐式布局。后来有学者在混合型公交网络设计中扩展了这种建模方案，在混合型公交网络中，城市中心线路采用网格结构布局，在所有位置提供4向公交服务(即双线路覆盖)；城市外围则采用枢纽和轴辐式结构，提供双向服务(即单线路覆盖)。这种混合型结构结合了枢纽型网络和网格型网络的特点，在乘客换乘便利性和运营商总服务距离之间取得平衡，规划方案取决于几个关键的决策变量，例如，网格区域大小、路线和站点间距，以及发车间隔[3]。此类模型后来陆续被调整，以允许线路和站间距的方向异质性[4]、环形辐射式公交网络设计等[5]。

CA模型通常假定需求在空间上是同质的或单中心的。然而，在现实世界中，许多多中心城市的出行分布在空间上是不同的，甚至是聚集出行的，这就决定了一些街区的公交网络比其他街区的线路和站点更密集。此外，在许多城市，特别是像北京这样的大都市，多种公交系统(例如，地铁、快速公交和普通公交)并存，形成一个为不同类型需求服务的多层次网络。例如，公交车价格便宜但速度慢，适合短途出行；地铁价格稍贵但速度快，适合长距离出行。一个特大城市的完整公交系统规划是很复杂的，因此，分层次的或特大城市的线网规划内容在文献中没有得到系统的论述。

本文讨论了地面公交在多方式公共交通系统中的作用，以及3种不同的地面公交子系统各自的功能和作用并定性讨论了子系统的规划程序及其原理；提出基于运营商和用户成本的连续体近似法模型搭建方法；以北京为例，介绍连续体近似法模型在实际中的应用。

1 线网层级及功能分析

大城市公交系统服务的出行距离范围较广，从1～40 km 长短不等，这些不同距离的行程应该得到不同的公交服务。长途旅行最好采用站间距长的服务，虽然是更长的两端到站距离，但也能使长途旅行乘客避免经历无数次的车站停靠；短途旅行最好采用站间距离短的服务。因此，需要提供一个服务于不同站间距离的分层级公交系统。

对于大城市而言，3个子系统应该是足够的，再多的子系统会带来边际效益递减。因此，按长度对旅行进行分类：长距离(10～30 km)、中距离(3～10 km)和短距离(1～3 km)。

长距离出行主要是通勤出行，集中在高峰时段，规划中应考虑在尽量少的停靠和换乘的情况下提供服务。在特大城市，通勤出行的数量特别多、时间特别长，地铁往往无法舒适地服务于所有的乘客。为此，应该使用公交车作为地铁的补充，增加额外的运力。例如，可以在平行于拥挤的地铁线路上部署具有长站间距的公交快线，并与地铁实现无缝连接，或部署在完全没有地铁服务的走廊上。

中等距离出行通常在空间和时间上比较分散。虽然有些人可能会因为出发地和目的地恰好在地铁线车站附近而得到良好的服务，但仍有大量出行应该由组织良好的普通地面公交提供更好的服务。这里的“普通”指一个能提供全面的中长距离覆盖的系统(即从城市的任何地方到10 km 内的任何地方)，其服务频率与地铁相当。中等规模城市(例如，巴塞罗那)的设计方法已经开发，并已证明了其价值。从理论和经验中可以看出，大城市中目前普遍存在的非常长的公交线路无法按计划运行，容易产生大间隔或串车现象[6]。因此，本文提出将特大城市划分为中等规模的区域(50～100 km2)，然后为每个区域设计一个高效、高频的公交网状系统。这些系统在边界处重叠，从一个区到另一个区的乘客可以很容易地换乘。由于中、长距离旅行距离在10 km 以下，因此，最多一次换乘就可以满足所有需求。

短距离出行服务的重点是提供最后一公里的接驳出行。由于其中一些行程可能已经由中、长距离公交系统提供了很好的服务，因此，在规划中应首先确定服务较差的区域，以便在那里部署线路。由于规模经济的原因，最后一公里服务的需求越低，其单位成本越高。因此，对于需求量小的地区来说，提供需求响应式公交服务或共享单车更为经济可行。

理想情况下，3 个子系统应按公交快线(长距离)、普通线路(中距离)、微循环(短距离)顺序规划。这种顺序，是因为普通公交系统路线靠近公交快线车站，这些站的位置是公交快线的部分规划成果。此外，最后一公里服务的需求在很大程度上取决于普通公交系统能满足的程度。公交快线应集中分布于轨道交通无法覆盖或轨道交通能力不足的大客流走廊，规划时以这些走廊为对象，结合乘客出行起点、终点分布逐一布设。因此，本文研究核心为普通线路公交系统规划，这个层级的线网规划不仅承上启下，而且因为其服务对象的分散性，规划方法不易掌握，因此，本文的研究也更具有现实意义。

2 基于运营商和用户广义成本最低的连续体近似法模型搭建

考虑一个长方形城市，其街道网格非常密集，如果需要的话，其中任何一条街道都可以用于布设公交线路。假设城市中已经铺设了服务于长距离出行的公交快线，需要设计一个为中距离出行服务的公交普线系统。

假设任意i区的面积为Ri，从i区到j区的出行需求(包括j=i时的区域内出行)近似地用平均出行生成率为λi,j(人·(h·m2)-1)描述，平均出行距离为li,j。由于大多数长距离出行会使用地铁或公交快线，本文重点关注区域内的出行，或者只跨越两个相邻区域的出行。区域网络上的所有公交车都是相同的，每辆公交车在当时交通状况下的巡航速度为v(km·h-1)；每站因上车/下车、车门操作、减速和加速而损失的停留时间为ts(h)。

为每个区选择两个主要的空间网络设计变量：所有公交线路双向总服务距离Li和物理公交站点的总数ni。为保证所有位置的优良服务，所有网络共享相同的公交服务发车间隔H，各地的线路和站点间距大致相等。假设每条线路都是双向服务，每个物理站都为双向的乘客服务，近似的平均站间距si为

对于公交系统来说，方格网是非常有效的[3]。因此，假设这些线路像方格网一样部署，线路间距是非常均匀的，而且是平均的，即

网格对于多区系统特别有效，因为如果相邻区的线路间距是彼此的倍数，那么两个网格就可以无缝连接，几乎不需要为跨区出行增加回路。这种连接功能可以通过限制所有地区的线路间距，从二次方的菜单中选择来实现[7]。

通常情况下，地区i的公交网络运营商成本取决于：(1)运营车辆的规模，按比例计算的购置成本；(2)单位时间内行驶的车辆总距离(km·h-1)，能源消耗和车辆磨损；(3)单位时间内行驶的车辆总时数，司机工资和车辆维修成本。事实证明，在大多数情况下，指标(1)和指标(3)是成正比的，因此，放在一起考虑。

首先，公交车单位距离行驶的实际时间由巡航该距离的时间1/v和停留在（2ni）/Li个站点的时间组成。因此，平均运营速度满足

等价于

影响车队规模Mi的因素包括：发车间隔H、总服务距离Li和运营速度。需要注意的是，所有车辆在1 h内行驶的总距离为

在一个发车间隔时间内，所有Mi辆车行驶的总距离应等于所有线路的总服务距离，即

因此，结合式(4)和式(7)，得到运营所需的车队规模为

一个乘客从i区到j区花费的时间包括：两端步行时间Ai,j；与间隔和预期换乘有关的等待时间Wi,j；车辆内乘坐时间Ti,j；对每次换乘带来的不便施加一个惩罚δ(以时间为单位)。

假设：(1)乘客以恒定的速度w(km·h-1)行走；(2)乘客到达离出发地和目的地最近的站点；(3)在这些站点之间出行，换乘次数最少；(4)在第一时间换乘。目标是保持合理的小间隔和相对稳定的公交车到达时间。在这些假设下，考虑两种类型的乘客：区域内的乘客，其出发地和目的地都在同一地区；区域间的乘客，其出发地和目的地分别属于两个相邻的地区。

对于区域内的乘客，预计在出发地的平均等待时间为H/2，假定至少有一次换乘，又增加了换乘期间的H/2 等待时间和对不便的惩罚，为H+δ；对于区域间的乘客，假设最多需要3次换乘，2次在区域内，1次在两个区域的边界，总的预期等待和惩罚时间为2H+3δ。则总等待和换乘惩罚为

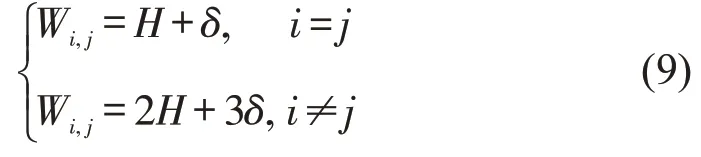
当公交车站在该区域内均匀分布时，每个车站大约服务于一个矩形的聚集区，其边长等于行距Si=4Ri Li和站距si=Li（2ni）。假设在附近有网格状的街道，则行程两端的平均步行距离约为这些间距之和的1/4。因此，任何乘客的总步行时间为

车内乘坐时间受行程长度和区域网络中车辆运行速度的影响。对于i区的区域内乘客，乘坐时间约为li,i。对于从i区到j区的跨区域乘客，如果这两个区的面积大约相等，那么在任何一个区的乘坐距离约为li,j/2。因此，总的乘坐时间约等于则总乘车时间为

式(4)～式(11)对任何区对都成立，只取决于决策变量，即H、Li和ni。关于发车间隔，只要H很小(例如，小于8～10 min)，乘客就会对其数值不敏感，并愿意换乘[8]。这些决策变量的最佳选择不仅取决于乘客和运营商成本之间的权衡，还取决于用于支持服务的特定城市街道。

理论上，每个区的路线间距随空间逐渐变化。本文执行二次方概念[9]，以便更容易地进行线路排列，这就决定了，以较小的优化损失为代价，一个区的线路间距相对于一个共同的“参考”间距S0来说，是以离散的指数尺度出现的，即

因此，网络决策变量Li可以等效地由S0和ki确定。

另外，由于Mi可以被解释为在i区运行系统所需的车队规模，如果运营商强制使用最大车队规模，可以简单地施加一个车队规模限制，设为，假定共包含N个区域，即

最后，选择执行一个可行的发车间隔下限Hmin，即

时间价值β用来将运营商的货币成本转换为以时间为单位的等价用户成本。通过确定决策变量的最佳值，使机构和用户在单位时间内的广义预期成本最小化。

式中：目标函数是运营商加用户单位时间的广义成本；系数cV和cM分别为每辆公交车每公里和每小时的单位运营成本；乘客的平均时间值用β表示。一些决策变量应该取整数值，为了表述简单，可以用一个实数来近似，本文通过基于梯度的搜索方法(例如，最陡下降法)解决，将它们四舍五入为最近的整数。约束条件为式(4)～式(14)，还可以根据不同城市的需要增加额外的约束条件，例如，对到达时间或等待时间加以限制等。

3 北京的案例分析

要为大城市制定全市性的计划，需要将城市划分为规模可控的区域，提供每个区域的需求目标，并为每个区域设计符合这些目标的公交系统。

3.1 分区方法

在分区之前，需要明确分区原则：(1)为尽量避免长线运营带来的大间隔或串车问题，每个区域的面积宜控制在50～100 km2；(2)每个区的形状尽量为长方形，边界尽量为道路，以便于形成形态规整的内部线网；(3)各区尽量以区内出行为主，区与区之间的出行为辅；(4)每个区的人口分布尽量比较统一。

关于实操层面的分区方法，有学者做过相关研究，并开发了针对特大城市分区的系统性方法，但整体系统成本和服务水平对分区结果并不十分敏感，因此在实践中，合理的分区可以结合分区原则进行人为划分[10]。

本案例主要采用人工分区方法，基于中心城6个行政区(标定为1～6)以及实际人口分布情况，划分了12个区域，基本满足分区原则，北京中心城区公交服务区域划分如图1所示。北京中心城区的区位特征如表1所示。基于北京市域宏观模型测算的不同区域之间和区域内部的出行距离如表2所示。其中，3e 代表3区东部，3w 代表3区西部，4nw代表4区西北部，4ne代表4区东北部，4se代表4区东南部，4sw代表4区西南部，5e代表5区东部，5m代表5区中部，5w代表5区西部。

表2 区域之间及区域内部预期出行距离Table 2 Expected trip distances between and within regions（km）

图1 北京中心城区公交服务区域划分Fig.1 Bus service district definition in central Beijing

表1 北京中心城区的区位特征Table 1 District characteristics in central Beijing

3.2 分区规划目标设定

完成分区后，应该为每个地区设定一个规划的需求目标。本文强调，不应该是对当前需求或预测需求的估计，而是对未来的一个愿景。当前的需求是当前服务的反映，而当前的服务在城市某些地方可能很差或根本不存在。

在北京的案例研究中，设定中心城区每天公交出行目标为1400 万人次，比目前的公交需求(包括使用公交快线的公交需求)高出约50%。然后将这一目标按比例分配到每天运营的17.5 h 内(5:30-23:00，平均每小时约80万人次，按照目前高峰小时系数，规划高峰小时将达到152 万人次)，再根据人口分配到各个分区。最后将产生的公交出行次数换算成每小时客运量，高峰小时公交出行次数如表3所示。

表3 高峰小时公交出行人次Table 3 Target transit trip number per hour in neighboring districts

3.3 基于连续体近似法的理想网设计

截至2019年，北京公交公司每年花费日常运营成本约5241.69 万元人民币，提供约231744 个公交车运营小时，每天覆盖348.56 万车公里，基本上只有普线网一个层级。北京高峰期的平均发车时间为5～8 min，约2/3 的运营成本与运营时间有关，可换算为cM=151 元·h-1，其余与运营里程有关，cV=5 元·h-1。2014年的居民出行调查显示，北京交通参与者每次出行平均花费63.2 min(1.05 h)，其中：14.5 min(0.24 h)用于步行，41.4 min(0.69 h)在车内，等待/换乘时间为7.3 min(0.12 h)。对于通勤交通，时间值设定为28 元·h-1[11]。模型中使用的其他参数值是基于历史数据的，v=18 km·h-1，w=5 km·h-1，δ=4 min。

利用本文设计的模型，通过MS Excel Solver中的标准非线性算法进行求解。该算法趋于快速收敛，通常在10 次迭代之内，梯度容差为10–3。每个案例的总计算时间(包括评估)在10 s左右。

参考间距为S0=2.5 km ，普线发车间隔H为4 min。各个区域网络的设计参数如表4所示。需要注意的是，大多数地区的线间距约为625 m，而位于城市外围的本地需求地区，例如，3w、4ne、4se 和5w，线间距较大，为1.25 km。

表4 区域网络的最优设计Table 4 Optimal design for district networks

根据《北京市地面公交线网总体规划》中干线、微循环线路的规划成果，干线公交车队总规模为3764 标准车，单方向线路总长度为3066 km，无新增公交站点，运营企业成本估算为每小时67.1万元人民币；微循环线路车队总规模为3300标准车，单方向线路总长度为2123 km，新增公交站点253个，运营企业成本估算为每小时46.5 万元人民币。通过本文的设计，普线公交车队规模为6244标准车，单方向线路长度为6531 km，站点数4825 个，运营企业成本估算为每小时143 万元人民币。经过线路重新设计后，总的公交车队规模为13008 标准车，比现状减少7%；单方向线路总长度为11720 km，减少60%；总站点数为5078 个，增加39%；由此产生的运营企业成本估算为每小时256.6万元人民币，降低5%。

由于现状公交线路基本为普线服务，因此，在不考虑规划干线和微循环线路服务水平的情况下，本文方案设计得出的乘客出行体验为：区间车平均出行速度约为15.3～16.2 km·h-1，与现状相当；乘客平均出行时间为0.89 h，比现状减少21%，其中等待、到站和乘坐时间分别为0.17，0.14，0.52 h，分别减少34%、43%和23%。可以看出，新的设计有可能使用更小的运营成本，同时产生一个明显更好的服务水平。而且可以预计，普线网基础上叠加上干线和微循环线路后，乘客等待时间、步行时间和车外时间将进一步压缩，乘客体验将继续得到提升。关键性能指标比较如表5所示。

表5 关键性能指标比较Table 5 Key performance metrics and comparison

应该注意的是，现状公交系统的统计数据与使用该系统需求相对应，即它包括了大部分与所提供的路线完全一致的出行。相比之下，新系统经过更为严格的评估，是针对随机的出发地和目的地，以及随机的出行方向。因此可以认为，新系统提供了更好的出行机会。

3.4 基于路网和兴趣点POI的网络校核

基于模型的输出结果制定一个可实施的设计方案，以适应现有的街道和潜在的车站位置。由于北京当地城市街道的不规则性，许多公交线路不得不被扭曲。这种不规则性通常是由城市核心区内的主要建筑(例如，故宫-紫禁城)或外围的不规则景观(例如，河流、山脉)造成的。例如，模型输出建议在1 区和2 区的“e-w”方向布置约16 条路线。然而，在各区的中心地带，只有6 条街道可以容纳跨区的交通路线。在这些情况下，铺设线路的原则按优先顺序递减：(1)确保跨区域连接；(2)根据准则尽可能均匀地分布路线；(3)允许重叠，必要时在当地绕行路线，既便于换乘，又能避免各区交界的中间地带由于分区误差带来的服务水平的显著差异，提高网络连续性。最后，所有地区的公交网络基本上都是网格状的，对于大多数高需求地区，实际可实施的定向地面公交服务距离在其各自推荐值的30%以内。所有地区的规划线路结果如图2所示。

图2 可实施的公交线路布局Fig.2 Implementable bus route layouts

4 结论

本文得到的主要结论如下：

(1)特大城市公交线网，按照服务距离分为公交快线、普线和微循环线路，且依次规划是比较合理可行的。普线网由于其服务的出行在时间和空间上更为广泛，是公交线网层级中最难规划的一个层次，也是本文论述的重点。

(2)普线规划可以通过用户和运营商成本的连续体近似法系统地确定。通过北京的案例，证明这种方法简单、有效。新的公交网络在相近的运行速度下通过更高频的服务、更直接的出行，提供了更好的乘客体验，体现在出行时间减少和可达性得到提升，同时在运营车队规模和线路距离上实现了显著节省。

(3)基于本文方法设计得到的公交线网，在小区域内基本上遵循网格状的布局思路，尽量减少不同线路共线的问题，集中车辆资源在更少的公交线路上以提供高频、高可靠性服务。但由于路网条件所限，在局部区域仍有共线现象存在。此外，由于本文只涉及到普线网规划，如果在设计的普线网基础上增加干线和微循环线路，不同层级线路共通道的情况将普遍存在，但这是合理的，可以保证不同出行距离的乘客有不同的线路选择。

(4)基于分区的方法比较适用于中距离出行的普线规划。为避免不同区域交接处由于分区误差可能带来的服务水平的显著差异，交接处的公交线路尽量重叠一段，避免单点交接，但仍无法避免不同分区方法导致的同一地区服务水平的差异，例如，换乘的增加。即系统优化不能保证每个个体的出行都得到优化。