基于不确定需求的电动汽车共享系统规划方法

李嫚嫚，杨京帅，赵建有，赵博选，丁楠

（长安大学，汽车学院，西安 710061）

0 引言

单向电动汽车共享是一种新兴的绿色交通模式[1]。该模式下，用户可在任意共享车站借还电动汽车，以完成出行。它可使出行者享受汽车出行的便利，而无需拥有汽车，也可提高汽车利用率，减少温室气体和CO 等有毒气体的产生，有助于解决交通拥堵和环境污染问题[2]。

然而，共享出行需求的潮汐性和不均衡性易导致站点车辆失衡，即部分车站电动汽车积压，而另一部分车站电动汽车短缺。站点车辆失衡不仅会降低客户满意度，而且会浪费系统资源。解决站点车辆失衡的主要方法是动态定价和车辆重位[3]。动态定价是通过给引起车辆失衡的出行定高价，给平衡车辆分布的出行定低价，改变出行需求分布，平衡站点车辆。车辆重位是通过将车辆从富裕车站移动到缺失车站，调整车辆分布。

单向电动汽车共享系统配置会影响出行定价和车辆重位方案，也受出行定价和车辆重位方案的影响。例如，购置的电动汽车给定了可重位车辆数；不考虑车辆重位，共享系统所需电动汽车数将会显著增加。为减少投资成本，获取最大利润，电动汽车共享服务商应对单向电动汽车共享系统配置与运营决策进行联合优化。Jorge 等[4]和Xu 等[5]分别考虑价格对出行需求的线性与非线性影响，构建非线性规划模型，设计模型求解算法，提供联合优化出行价格、车辆重位方案和电动汽车购置规模的方法。但是，上述方法忽视了共享出行需求的随机性，设计的共享系统与运营方案鲁棒性较差，无法帮助电动汽车共享服务商获取最大利润。

为此，本文考虑共享出行需求的时变性和随机性，以最大化利润为目标，构建以共享车站规模、电动汽车规模、调度员规模、出行价格、车辆重位和人员重位为决策变量的一个混合整数规划模型，并基于外点法设计模型求解算法，提供单向电动汽车共享系统规划与运营决策支持方法。在此基础上，通过数值实验，解析共享需求随机性、共享需求弹性以及共享需求量对共享电动汽车系统的影响规律。

1 问题描述与建模

1.1 问题描述

某共享电动汽车公司拟在一个区域经营I个共享车站，并给共享车站的每个停车位配备充电桩。经营区的每个停车位日租金为Cl元。共享车站i（i∈I）处最大可租用停车位为Lmax,i个。

共享出行需求是不确定的，可用S种典型需求情景模拟[6]。1年中，需求情景s（s∈S）的发生概率为Hs，所有情景发生概率之和为1，即而且，共享出行需求具有时变性，故需将1 d分为相等的若干个小时段，如15 min 为一个时段，考虑每个时段的需求。情景s（s∈S）中，时段t（t∈T），车站i,j(i,j∈I)间的最大潜在需求为di,j,s,t,0，且为已知量。共享出行需求也受出行价格影响，会随价格的升高而不增，可表示为di,j,s,t,1=Φ(pi,j,s,t,di,j,s,t,0,Ei,j,s,t)。

为调整电动汽车分布，减少电动汽车配置量，共享电动汽车公司会雇佣一批调度员，重位电动汽车，如图1所示。当图1(b)可执行时，电动汽车共享系统所需电动汽车数为5辆；否则，为6辆。每个调度员的日工资为Cr元。调度员自己利用折叠电动自行车调整位置。

图1 规划层与运营层间的相互影响Fig.1 Interaction between planning and operational decisions

提供共享服务的电动汽车是同质的。每辆车日折旧为Cv元。在运营过程中，每辆纯电动汽车必须以满电状态开始服务。纯电动汽车的续航里程大于任意两车站间的距离。每天开始时，纯电动汽车都是满电状态。纯电动汽车的行驶速度为Vckm·h-1。根据该行驶速度，可得各车站间的纯电动汽车行驶时间为Tc,i,j个时段。每个时段纯电动汽车的耗电成本为Cf元·时段-1。同理，根据电动自行车行驶速度Vbkm·h-1，可得各车站间的电动自行车行驶时间为Tb,i,j个时段。

上述情景下，该共享电动汽车公司应如何配置车位、车辆和调度员，如何定价、重位车辆和人员，获得最大利润，是本文要解决的问题。

1.2 问题建模

首先，利用模型对上述问题进行描述。为减少跟踪车辆和调度员位置的变量数，以车辆状态和车站集计车辆，人员状态和车站集计人员建模，如图2所示。每种情景，每个时段，每个车站的车辆状态仅有3种：重位、等待和服务客户，每个车站的调度员状态也仅有3种：重位、等待和重位车辆。所以，以状态和车站集计车辆和调度员，可将每种情景，每个时段，跟踪车辆位置的变量从I×I×N(N为车辆总数)缩减到I×I×3，跟踪调度员的变量从I×I×R(R为调度员总数)缩减到I×I×3。

图2 电动汽车与调度员集计示意图Fig.2 Illustration of aggregation of electric car and personnel

据此，可将上述问题用数学模型描述如下。

(1)已知参数

I——共享车站集合，i,j∈I；

T——时间段集合，t,u,w∈T={1,2,…,Tmax} ；

Nd——共享电动汽车系统年运营天数；

S——需求场景集合，s∈S；

Cl——停车位日租金；

Cr——调度员日工资；

Cd——电动汽车日折旧；

Cf——电动汽车一个时段的耗电成本；

Hs——每个需求场景的发生概率；

Tc,i,j——车站i,j间电动汽车行驶时间；

Tb,i,j——车站i,j间电动自行车行驶时间；

Tr,i,j——车站i,j间包括充电时间的电动汽车行驶时间；

Lmax,i——车站i处最大可租用停车位数；

Tmax——每个运营日的最后一个运营时段；

di,j,s,t,0——情景s，第t时段车站i,j间潜在共享出行需求量，即共享出行服务免费时的需求量；

Ei,j,s,t——情景s，第t时段车站i,j间共享出行需求价格弹性；

di,j,s,t,1=Φ(pi,j,s,t,di,j,s,t,0,Ei,j,s,t)——情景s，第t时段车站i,j间共享出行需求与出行价格关系式。

(2)决策变量

li——共享车站i处租用的车位数；

N——购置的车辆数；

P——雇佣的调度员数；

hi,s,t——情景s，时段t开始时，车站i处的电动汽车数；

fi,s,t——情景s，时段t开始时，车站i处的调度员数；

di,j,s,t——情景s，第t时段，车站i,j间需求被服务量；

pi,j,s,t——情景s，时段t，车站i,j共享服务定价；

yi,j,s,t——情景s，时段t，车站i,j间车辆重位数；

zi,j,s,t——情景s，时段t，车站i,j间的调度员重位数。

(3)辅助决策变量

Ai,s,t——情景s，时段t开始时，车站i处的满电状态车辆；

qi,s,t——情景s，时段t，车站i服务的客户；

qi,s,t,-——情景s，时段t，服务客户到达车站i的车辆；

Ri,s,t,-——情景s，时段t，服务客户到达车站i，且充满电的车辆；

xi,s,t——情景s，时段t，从车站i出发的重位电动汽车；

xi,s,t,-——情景s，时段t，到达车站i的重位电动汽车；

Xi,s,t,-——情景s，时段t，到达车站i，且充满电的重位电动汽车；

wi,s,t——情景s，时段t，从车站i出发的重位调度员；

wi,s,t,-——情景s，时段t，到达车站i的重位调度员；

as,t——情景s，时段t开始时，正在服务客户的电动汽车；

bs,t——情景s，时段t开始时，正在重位的电动汽车。

式(1)为目标函数，最大化平均日利润。式(2)为停车位约束，每个共享车站租用的停车位小于等于最大可租用停车位。式(3)～式(23)适用每个情景。式(3)约束共享电动汽车系统服务的需求小于等于共享需求。式(4)～式(16)为针对共享电动汽车的约束：式(4)统计了情景s，时段t，车站i服务的需求数；式(5)统计了情景s，时段t，服务客户到达车站i的电动汽车数；式(6)为电动汽车守恒约束；式(7)约束每个时刻，车站处的电动汽车小于等于停车位；式(8)指定一天开始时，可用电动汽车等于车站电动汽车拥有量；式(9)约束每时段，从车站离开的电动汽车小于等于该处可用电动汽车；式(10)统计了情景s，时段t，服务客户到达车站i，且充满电的电动汽车数；式(11)统计了时段t，到达车站i，且充满电的重位车辆数；式(12)统计了正在服务客户的电动汽车数；式(13)统计了正在重位的电动汽车数；式(14)统计了每个时段开始时，车站可用电动汽车数，如图3(a)所示；式(15)统计了每个时段开始，车站拥有的电动汽车数；式(16)指定单向电动汽车共享系统运营1 d后，需还原车辆分布。式(17)～式(23)为针对调度员的约束：式(17)为调度员守恒约束；式(18)计算时段t，车站i处重位车辆的调度员数；式(19)统计了时段t，重位车辆到达车站i的调度员数；式(20)统计了时段t，车站i处重位的调度员数；式(21)统计了时段t，重位到达车站i的调度员；式(22)约束车站i的重位调度员和重位车辆的调度员总和小于该车站调度员拥有量；式(23)描述了上下两个时段车站调度员拥有量的关联，如图3(b)所示。式(24)指定了决策变量取值范围。

图3 时段t 车站i 的电动汽车与调度员变化Fig.3 Changes of electric car and personnel at station i in interval t

2 算法设计

(3)除此之外，本文所建模型为一个混合整数非线性规划模型。Duran 和Grossmann[7]提出的外逼近算法是求解混合整数非线性规划模型的一种经典方法。其核心思想是寻找一系列上下界，直至上下界差异不超过预设容忍度ε。

当Gi,j,s,t是一个上凸函数时，式(3)仅在最优解处有效，模型可转换为

因此，利用外点法求解本文模型的误差可完全由外逼策略g(di,j,s,t) 控制，而且仅需迭代一次就可求解到小于ε的最优解。当设定求解误差为ε时，外逼策略应满足

式中：|I|——共享车站数量；

|S|——需求情景数；

|T|——时间段数。

当共享出行需求是出行价格的下凸函数时，如式(29)的线性函数，式(30)的指数函数以及式(31)的幂函数，Gi,j,s,t是一个上凸函数。根据上凸函数特征可知，Gi,j,s,t的一阶泰勒展开式大于等于Gi,j,s,t。又因di,j,s,t是整数变量，因此，Gi,j,s,t可仅在整数点处进行一阶泰勒展开。进一步分析可知，将泰勒展开式中的导数调整成割线斜率，可获得相对更紧的外逼函数，如图4所示。同时，依据求解误差，可仅在部分整数点处，对Gi,j,s,t进行一阶泰勒展开，包括展开点选择的外点法。具体流程如下：

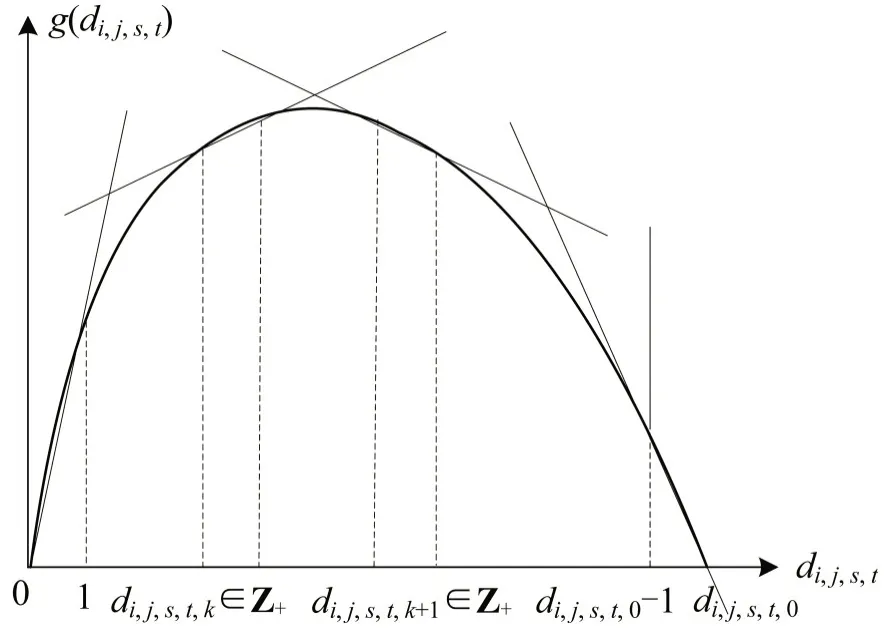
图4 基于割线的外逼策略Fig.4 Outer-approximation scheme based on secant

Step 1 如果s,t,i,j所有组合遍历，转Step 5；否则，找一个新s,t,i,j组合，转Step 2。

Step 2 如果di,j,s,t,0=0,Ω=-1，转Step 1；如果di,j,s,t,0=1, Ω={(0,1)}，转Step 1；否则，初始化Ω={([0 ,1],[di,j,s,t,0-1,di,j,s,t])},k=1,m=1 。 设定

Step 3 如果k≤m，则寻找两条割线的相交点Ii,j,s,t,k=Ω{k} ；否则，转Step 1。

Step 4 如果Ii,j,s,t,k∈Z+,Δ=Gi,j,s,t(Ii,j,s,t,k)-ϒscant(Ω{k} (1),Ii,j,s,t,k)(ϒscant(Ω{k} (1),Ii,j,s,t,k)为由Ω(k)(1)中两点确定的割线函数，在Ii,j,s,t,k处的函数值)，当Δ≤δ,k=k+1；否则，m=m+1，Ω{k} (1)=[Ii,j,s,t,k,Ii,j,s,t,k+1] ，Ω{m} (2)=[Ii,j,s,t,k+1,Ii,j,s,t,k+2] ，转Step 3。否则，表示向下取整)，当Δ≤δ,k=k+1；否则，m=m+1，表示向上取整)，转Step 3。

Step 5 ∀s,t,i,j，如果Ω=-1，将Gi,j,s,t≤0 添加到模型约束；否则，Gi,j,s,t≤ϒscant(Ω{k} (ς)),∀k,ς=1,2。

Step 6 利用分支定界法求解OP-2。

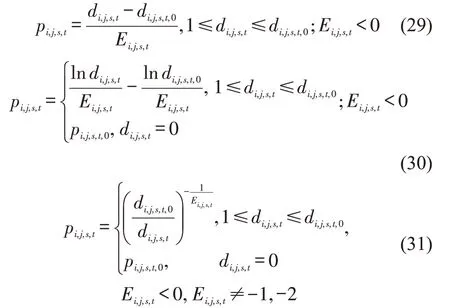
3 数值试验

数值试验中，外点法利用MATLAB 2019b 编译，模型OP-2 利用MATLAB 2019b 调用GUROBI 9.1.1求解。

3.1 算例设计

每个需求情景中OD 对间的潜在需求量等于基本需求与需求乘子的乘积。以[0,5] 均匀分布生成OD 对基本需求[5]；以符合[-σ,0.2-σ] 和[σ-0.2,σ],0.2 ≤σ≤1 的均匀分布生成需求乘子。各共享车站的最大可租用车位为300 个。各共享车站间的距离以符合[5,15] 的均匀分布生成(单位：km)。电动汽车行驶速度为25 km·h-1，电动自行车的行驶速度为20 km·h-1。车位租用成本为100 元·d-1，调度员日工资为90元·d-1，电动汽车日折旧为60 元·d-1。共享出行需求与出行定价为线性关系，如式(29)，其中，Ei,j,s,t=-0.2,∀i,j,s,t。算例中不考虑电动汽车的充电时间。

3.2 算法效率分析

GUROBI 9.1.1 虽然也可直接求解算例(非凸非线性规划模型)，但其求解效率比本文设计的外点算法差。如表1所示，GUROBI 9.1.1 求解I×T=7×24 规模案例所用时间超过3600 s，而外点法所需时间小于3 s。

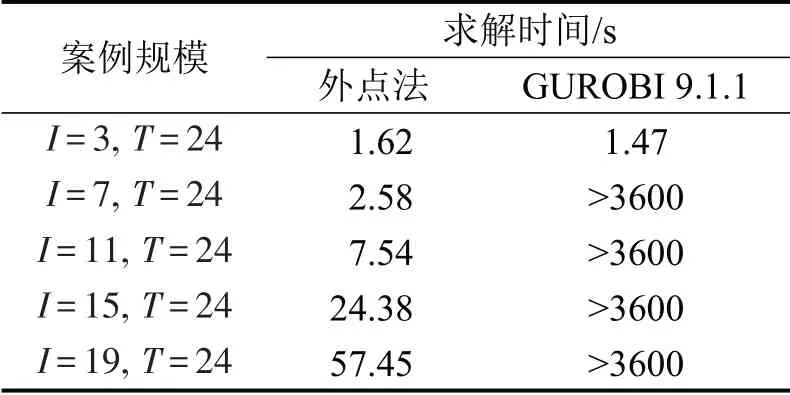
表1 设计算法与GUROBI的求解速度对比Table 1 Comparison of solving speed between designed algorithm and GUROBI

进一步，外点法求解效率随时间段数量的变化也被分析，如图5所示。图5中的求解时间针对的站点规模为I=19。它显示，当时间段增加，外点法的求解时间将显著增加，且增速加快。因此，建议问题时间段不易分的太细，增加求解负担；同时，也建议进一步提高外点法求解效率。

图5 外点法求解时间随时间段数量的变化Fig.5 Change of computation time of outer-approximation approach over number of intervals

3.3 共享需求不确定性的影响

图6对比了考虑需求不确定性与平均需求(各情景需求平均值)下的共享电动汽车系统利润。图中的差异比为5 个案例的平均值。每个案例的差异比为

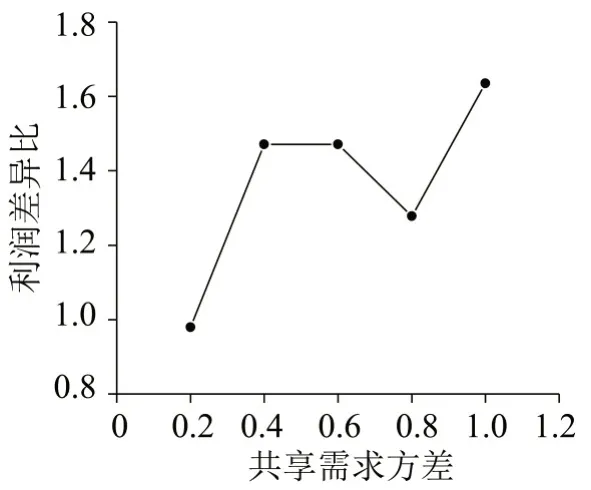
图6 不确定需求与平均需求下的共享电动汽车系统利润对比Fig.6 Comparison between profit of one-way electric carsharing systems with uncertain demand and average demand

式中：G——差异比；

U——不确定需求下的利润(元)；

C——平均需求下的利润(元)。

图6显示，考虑需求不确定性配置的共享电动汽车系统获得的利润高于以平均需求配置的系统(G＞0)，可多获高达90%以上的利润，表明在配置电动汽车共享系统时，应考虑共享需求的不确定性。这主要是因为共享电动汽车系统可获利润是共享需求的非线性函数，因此，高需求下的利润并不等于低需求下的利润之和。

同时，观测了不同需求方差下的共享电动汽车系统特征，如表2所示。表2显示，共享电动汽车系统利润随需求方差的增大而增加，增加的利润来源于服务了更多的共享出行需求，也源于更高的服务价格。

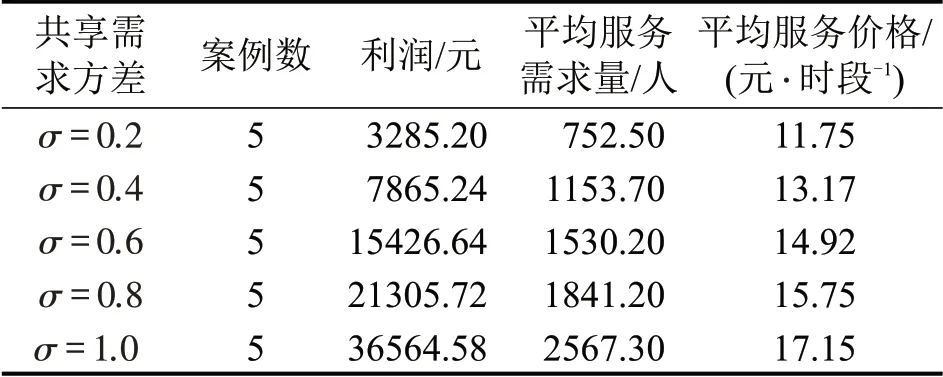
表2 不同需求方差下的共享电动汽车系统特征Table 2 Characteristics of one-way electric car-sharing system under different demand variations

3.4 敏感度分析

本节分析需求价格弹性和需求量对共享电动汽车系统的影响，为共享服务商提供管理建议。表3为不同需求弹性下的共享电动汽车系统特征。其显示，共享电动汽车系统利润随需求价格弹性绝对值的增加而迅速下降。这是因为共享电动汽车系统的服务量和服务价格都下降了。当需求价格弹性绝对值等于或大于0.3 时，共享电动汽车系统将无法获利。这些结果表明，共享需求价格弹性对共享电动汽车系统利润有显著影响，建议共享电动汽车服务商在配置系统、设计系统运营策略前，对拟服务区域的共享出行需求价格弹性展开深入调查。

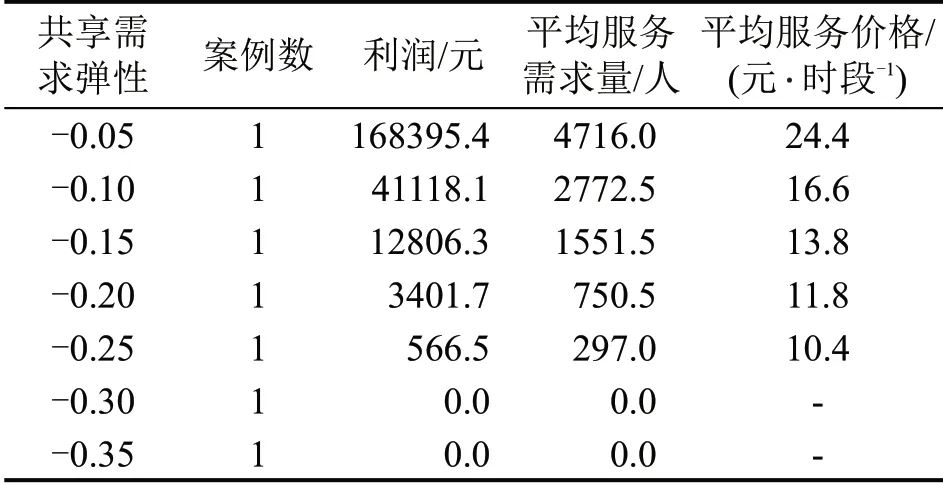
表3 不同需求价格弹性下的共享电动汽车系统特征（σ=0.2）Table 3 Characteristics of electric car-sharing system under different price elasticities of demand（σ=0.2）

表4为不同共享需求量下的共享电动汽车系统特征。它显示，共享电动汽车系统的利润、平均服务需求量和电动汽车配置数都随潜在共享需求的增加而增加，表明潜在共享需求增加时，共享电动汽车服务商应为系统配置更多的电动汽车和车位。潜在共享需求低于一定水平时，如案例中需求比低于0.6 时，共享系统将无法获利。这意味着从盈利角度，当潜在需求较低时，电动汽车共享业务不应开展。

表4 不同需求下的共享电动汽车系统特征（σ=0.2;Ei,j,s,t=-0.2,∀i,j,s,t）Table 4 Characteristics of one-way electric car system under different demand quantities

4 结论

本文以多情景处理随机需求，构建了融合车辆重位、调度员重位以及出行定价决策的共享电动汽车系统配置模型。针对3 类共享出行需求价格弹性函数，基于割线设计了用于模型求解的外点法，提供了动态随机需求下的共享电动汽车系统最优配置方法。通过案例分析得知：

(1)共享出行需求的不确定性会显著地影响系统利润；

(2)共享电动汽车系统利润随需求方差的增大而增加；

(3)共享电动汽车系统利润随需求价格弹性绝对值的增加而迅速下降；

(4)共享电动汽车系统利润、所需电动汽车和停车位都随潜在共享需求的增加而增加。