数据驱动的共享单车停放区规划方法研究

郭彦茹，罗志雄，王家川，何方*

（1.北京市交通信息中心，北京 100076；2.清华大学，工业工程系，北京 100084）

0 引言

共享单车方便了最后一公里出行，促进慢行交通发展，但其乱停乱放会占据紧张的道路资源，降低通行效率，增加交通风险[1]。为解决这个难题，政府部门拟推出“共享单车入栏管理”思路[2]，即在城市典型局部区域(例如地铁站周边区域)规划共享单车停放区，并采用电子围栏技术确保共享单车在停放区锁车结算。然而，上述规划在宏观和微观两个层次均面临挑战。宏观层面上，停放区的选址和定容对于满足城市居民出行需求和提高通勤便利非常重要。微观层面，停放区内部的停车位布局对混合交通流(行人、自行车甚至汽车)产生一定影响。共享单车停放区改变道路资源利用现状，并影响混合交通流的移动，因此，如何优化停放区内部停车位的布局以提高混合交通流下的通行安全和通行效率亟待解决。

宏观层面，García-Palomares 等[3]采用基于GIS的方法计算潜在共享单车出行需求，并通过最小化衔接距离和最大化需求满足来确定共享单车停放区的位置和容量。Çelebi等[4]假设停放区可以满足一定距离内的需求，通过集-覆盖模型进行需求分配，并加入排队模型描述服务水平，从而实现需求不确定下的规划。Lu等[5]进一步利用层次聚类，K中心点聚类和共享单车出行需求数据获取可行停放区，并结合停车激励方法，通过情景仿真的方式实现社会成本最小化的停放区选择。王瑜琼等[6]考虑位置识别率的影响，分析共享单车不同奖惩机制设计在博弈均衡情形下对用户停车行为的影响。

微观层面，混合交通流之间互动影响明显，其关键为人、自行车、汽车的混合交通流仿真模型。传统方法以社会力模型[7]及其各类变种为主。Moussaïd 等[8]考虑行人避撞的主动方向选择，并结合社会力确定人的加速度。Guo 等[9]将上述模型用于人和自行车的混合交通流仿真，并进行实验验证。Treiber等[10]提出车辆的智能驾驶模型，利用与前车的距离和速度关系确定车辆加速度。Chao等[11]将智能驾驶模型和社会力模型结合进行行人、汽车的混合交通流仿真。

本文从宏观到微观层面递进规划共享单车停放区。宏观层面考虑停放区选址和定容问题，采用DBSCAN 聚类算法确定可行停放区选集，并建立考虑共享单车使用者出行选择的混合整数模型优化共享单车停放区位置和容量，以满足出行需求并提高通行效率。与既有研究不同，微观层面考虑各停放区内部停车位布局问题，将停放区离散化为共享单车停车位，建立行人、自行车、汽车的混合交通流仿真模型，并通过基于代理模型优化方法决定共享单车停放区具体布局，以提高交通效率并降低交通风险。

1 停放区选址定容

宏观层面主要考虑共享单车使用者进入/离开局部区域的停/取车需求。合理配置停放区可以方便居民出行(靠近地铁站出入口等主要起点和终点)并满足停取车需求(足够大的停放区容量)。

1.1 可行停放区

本文采用DBSCAN[12]和现场调研的方式确定可行停放区选集。DBSCAN 是基于密度的聚类方法，通过相邻点距离和数量阈值将相邻的一系列点分为一类，并标记出类外点。该方法不需要提前给定聚类数量，但需要合适的参数“ε”(相邻点距离上限)和“min Pts”(相邻点数量下限)。本文结合共享单车订单停取车点位置数据，通过多参数试验评价确定合适参数，从而得到共享单车常用停/取车需求点。聚类组成反映该类停/取车需求，其类中心通常作为需求点。现场调研根据场地情况决定某个需求点是否可以作为停放区(例如地铁站出口通常是一个聚类位置，但是按照安全疏散规定无法作为停放区)，并根据道路条件确定该停放区容量上限。

1.2 选址与定容模型

本文通过构建混合整数线性规划模型来优化共享单车可行停放区的位置和容量。对于给定区域，例如地铁站周边300 m 范围内，主要需求为共享单车使用者进入区域还车(在地铁站入口附近停车)和离开区域取车(在地铁站出口附近取车)，较少有需求在该区域内同时取车和还车。因此，本文考虑A 类和B 类两类共享单车使用者。A 类使用者对应取车需求，其步行至共享单车停放区，并租赁共享单车，然后骑行离开。B类使用者对应还车需求，其骑行至共享单车停放区，并锁车归还，然后步行至目的地。图1为A类、B类使用者路径选择、共享单车停放区选择、交通模式选择的示意图。为简化模型，并聚焦局部区域，我们将A 类使用者区域外复杂目的地和B 类使用者区域外复杂起点等效为局部区域边界节点，如节点1和节点16所示。模型参数和变量定义分别如表1和表2所示。

表1 参数与定义Table 1 Parameters and definition

表2 变量与定义Table 2 Variables and definition

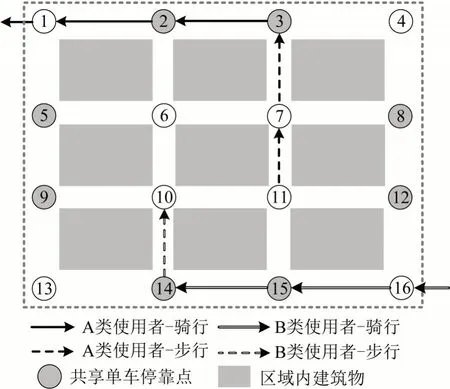
图1 共享单车A类、B类使用者选择示意图Fig.1 Route and mode choice illustration of bike-sharing users

该混合整数规划模型(MIP)为

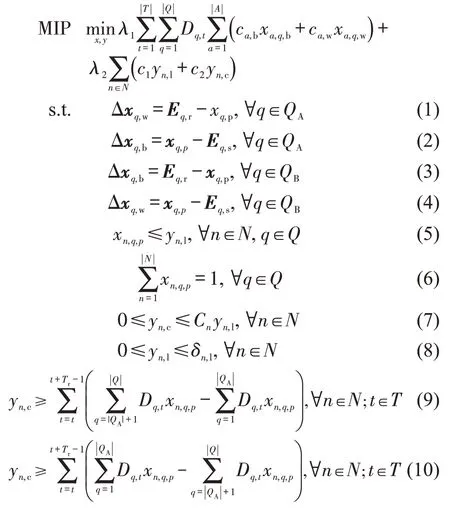
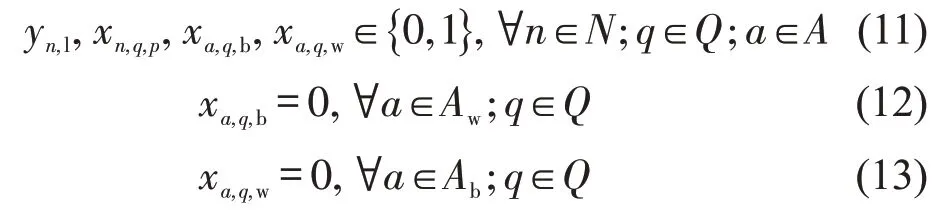
上述模型中，目标函数最小化出行时间成本和停放区建设成本的加权和。式(1)和式(2)分别保证A 类使用者步行从起点到停放区和骑行从停放区到终点。式(3)和式(4)分别保证B类使用者骑行从起点到停放区和步行从停放区到终点。式(5)确保共享单车使用者仅能在停放区停/取车。式(6)确保每个订单仅选择一个停放区。式(7)确保节点n作为停放区的容量范围为[]0,Cn；非停放区的容量为0。式(8)确保停放区仅能是备选节点，即δn,l=1 的节点。式(9)和式(10)保证停放区容量大于一定时间段内的净停车需求和净取车需求，该时间段长度由行业经验和政府对企业调度管理的要求确定。式(11)为通用0-1约束。式(12)和式(13)分别为步行专用道和骑行专用道的使用限制。

2 停车位布局

停放区位置和容量确定之后，单个停放区内部停车位布局仍需优化，如图2所示，采用混合交通流仿真和基于代理模型优化停车位布局。本文将停车位离散为多个可行停车位方块，如图2(b)虚线方框所示。对任意方块i，其设计变量xi∈{0 ,1} ，其中xi=1代表设置停车位，xi=0 则相反。

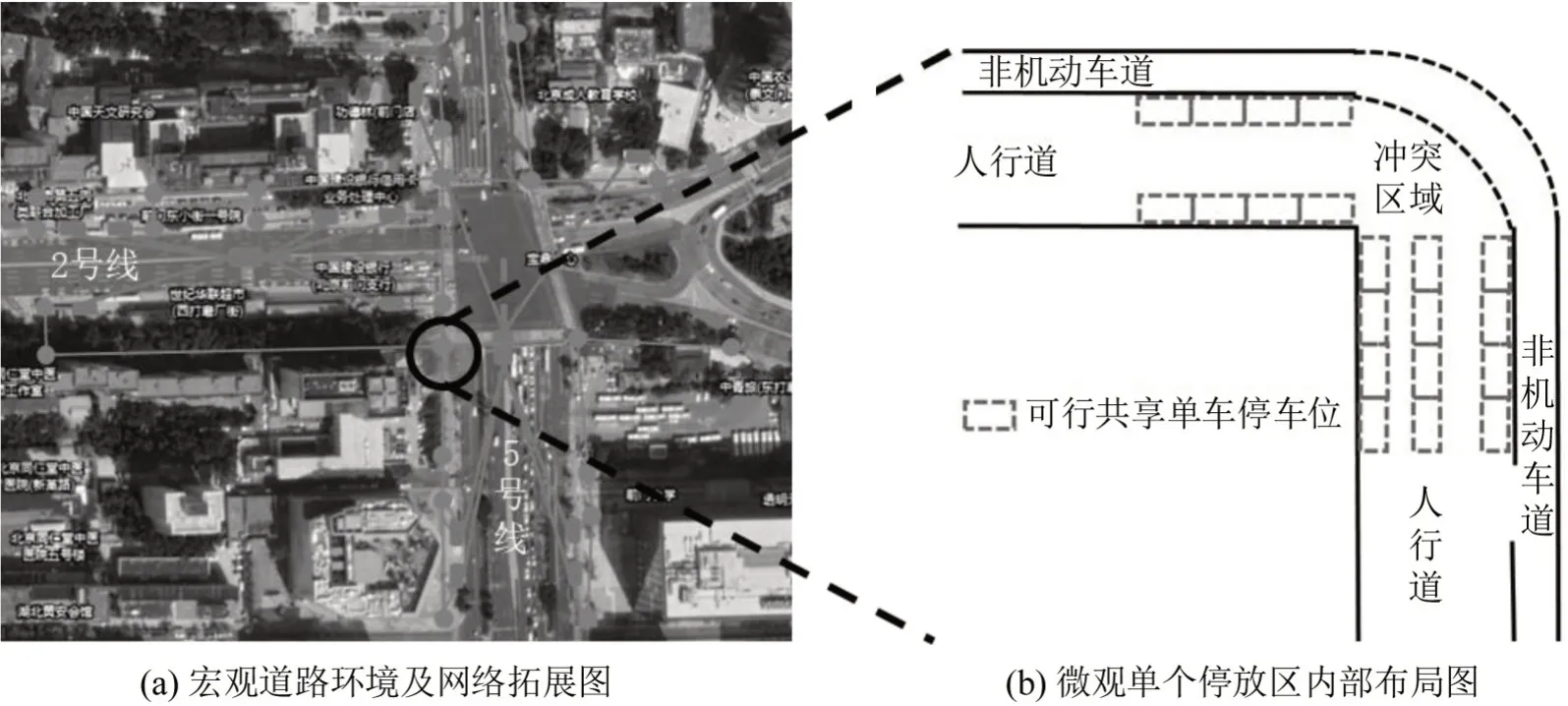
图2 宏微观联系图Fig.2 Relationship between macro-level and micro-level problem

2.1 混合交通流仿真

基于实际需求，考虑行人、自行车和汽车的混合交通流仿真。行人采用半径为rp的圆进行建模，自行车采用相切且半径分别为rbs,rbm,rbe的3个圆进行建模[9]，汽车采用长宽分别为cl,cw的矩形进行建模，如图3所示。

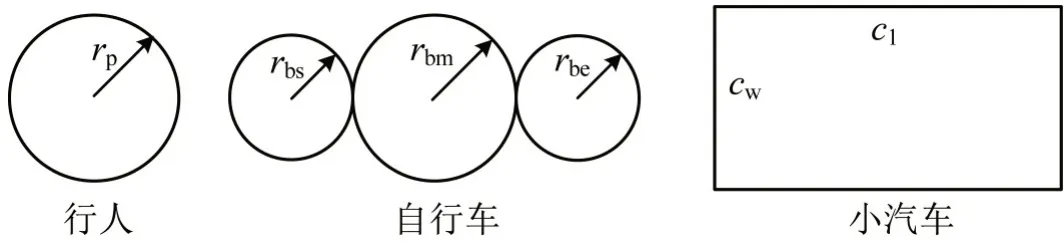
图3 行人、自行车和小汽车示意图Fig.3 Illustration for pedestrian,bike,and car

通常来说，出行者会进行3 个层次的决策[13]，分别是目的决策，路线决策和移动互动。在仿真中，假设出行者目的已知，仅决定最短路线[14]和移动互动。移动互动由改进认知模型[8]进行仿真，其假设行人充分认知道路状况并根据目的地和道路状况确定前进方向，即

式中：α0为直接前进方向，即连接目的地与当前位置的向量，可选前进方向范围为[α0-ϕ,α0+ϕ] ；f(α)为沿着α方向与其他交通参与者及道路边界发生第1次碰撞的距离(无碰撞时，f(α)=dmax)。式(14)考虑行人会选择无碰撞且偏离程度小的前进方向。给定行人偏好速度大小vi,0，因行人需要碰撞避免时间τ，故行人在给定方向的预期速度大小为

拥挤情况下，物理层面互动不可避免，故考虑事物j对行人i的影响力为

式中：k为合适参数；g(i,j)为i,j影响程度，例如g(i,j)=max{0,ri+rj-dij} ，ri和rj分别为交通参与者的影响范围，dij为i,j之间的距离;nij为j到i的方向向量由此行人的加速度为

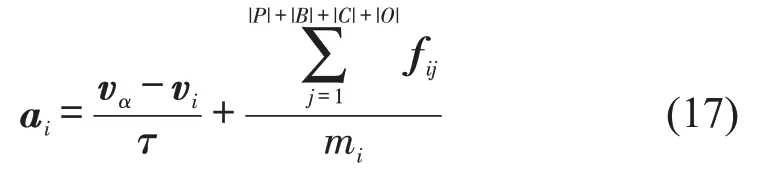
式中：vα为预期速度；vi为当前速度；P,B,C,O分别为行人、自行车、汽车和道路障碍集合；mi为行人i虚拟质量。自行车使用者假设按照最短用时来选择停车位置，即

式中：vc和vw分别为骑行、步行速度；li为第i个停车位置；o为当前位置；d目标位置。自行车使用者的目标速度和加速度计算方式与行人一致[9]，但考虑其模型组成3 个圆形中受力之和。换道对行人、自行车影响小，故假设汽车沿给定道路行驶，加速度由智能驾驶模型[10-11]决定，即

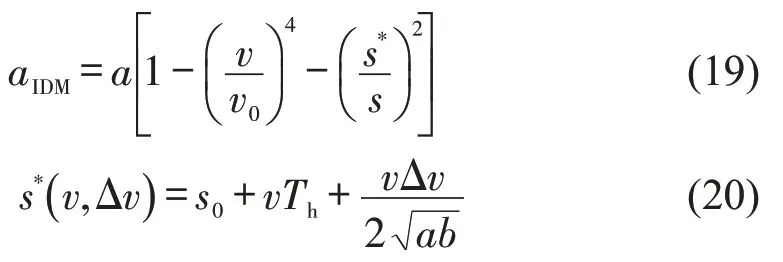
式中：a、b分别为偏好加速度和刹车速度；v、v0分别为当前速度和偏好速度；s、s0分别为与前方物体的距离和偏好距离；Δv为与前方物体的速度差；Th为偏好车头时距。考虑行人、共享单车使用者、汽车使用者集合分别为P,B,C对于任意交通参与者i，本文记录其出发时间和离开仿真区域(或到达区域内目的地)分别为ti,s和ti,e，得到仿真交通流总通行时间为

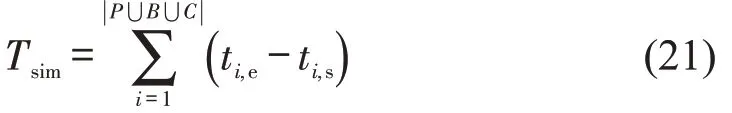
考虑密度高风险高原则，计算仿真场景中时空点(t,i分别代表时间和空间)行人、骑行者混合密度di,t，给出单个时空点风险系数为

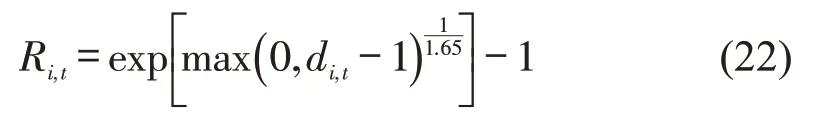
该风险系数在密度小于2 人(车)·m-2时很小，大于6时则急剧增加，符合直观。考虑仿真开始和结束时间分别为Ts和Te，空间点划分为I个，将时空点风险累加，得到整个仿真时空场景的风险指数为

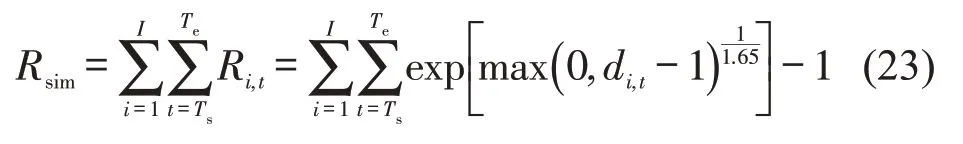
2.2 基于代理模型的优化算法

代理模型优化在交通基础设施规划中应用广泛[15]。该方法首先利用2.1节混合交通流仿真建立变量(停车位布局变量)与目标函数(仿真交通流总通行时间与风险指数加权和)的映射关系，即代理模型，并迭代优化代理模型给出新一轮变量。本文选择克里金模型作为代理模型，其基本形式为

式中：Z()· 代表0均值，σ2方差，相关系数的高斯随机过程，且；x为向量化的自变量；y为目标函数预测值；x(i)为已知自变量集合中的第i个自变量；x(ki)为对应变量的第k个值。采用Sacks等[16]的推导结果，其预测式为

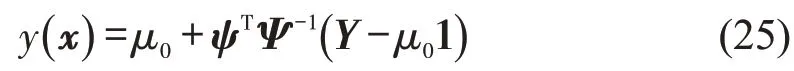
式中：Y为已知自变量集合对应的一组目标函数，(1TΨ-11)-11TΨ-1Y。R中的超参数则通过最大化似然函数LLF(θ,p)=-nlnσ2(θ,p)-ln |Ψ|获得，其中该算法框架如图4所示。

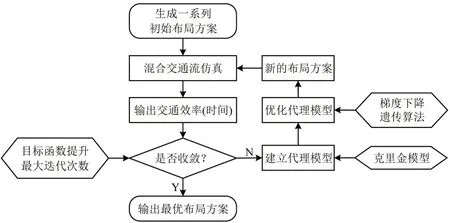
图4 基于代理模型的优化框架图Fig.4 Framework of surrogate-based optimization

3 算例及结果分析

3.1 .聚类选择不同参数敏感性分析

本文采用北京市崇文门地铁站周边某天共享单车订单起终点数据进行聚类，如图5所示。通过不同参数试验，并综合选择具有合适聚类数量，较小的类中距离和较少噪点数量的结果，如图6所示。选取其中箭头指向点，该聚类结果类中距离较小，需求衔接距离短，对应参数为ε=8 m,min Pts=30。

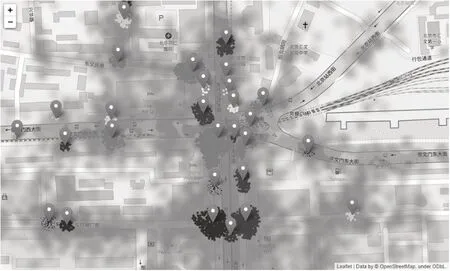
图5 崇文门地铁站周边共享单车订单数据及聚类结果Fig.5 Clustering results and bike-sharing trip data around Chongwenmen subway station

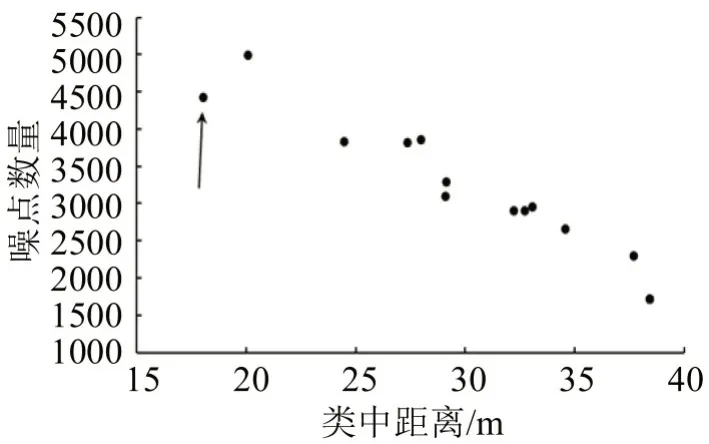
图6 合适参数的帕累托结果Fig.6 Pareto results of suitable parameters

3.2 选址定容模型

基于聚类结果和现场调研确定可行停放区，结合道路结构建立崇文门地铁站周边的道路拓扑网，如图7所示。拓扑网道路长度采用真实数据，其中地铁站内部(点10、28)及与出口间道路为步行专用道。除地铁内部和出口外，其他节点均为可行停放区。A 类、B 类共享单车使用者各时段总数量如图8 所示，基于地铁刷卡数据和现场调研结果按比例分配到路网的各个端点，即1,4,16,27,29,36,39,40。

给定不同调度时间和不同出行成本、建设成本权重，求解1.2节中的混合整数规划模型，得到不同调度时间下的帕累托解，如图9所示。结果显示，在停放区容量约束下，调度时间为15 min和30 min时，出行成本可以实现最小化，即骑行者按照最短路径出行均能找到共享单车停放区，有助于共享单车有序停放。此外，降低企业调度时间有助于减少出行成本和建设成本。北京市现有共享单车“异常聚集”管理要求为30 min 内响应，1 h 内完成调度。该要求在“入栏结算”政策和停放区容量约束下无法达到最低出行成本，且伴有较高建设成本，因此可适度提高调度管理要求至30 min。图8的帕累托曲线可以帮助政府在针对不同出行和建设成本权重时做出决策，例如箭头对应点，其调度时间要求为30 min，其中点19, 22, 27, 33, 38(图7)为共享单车停放区。

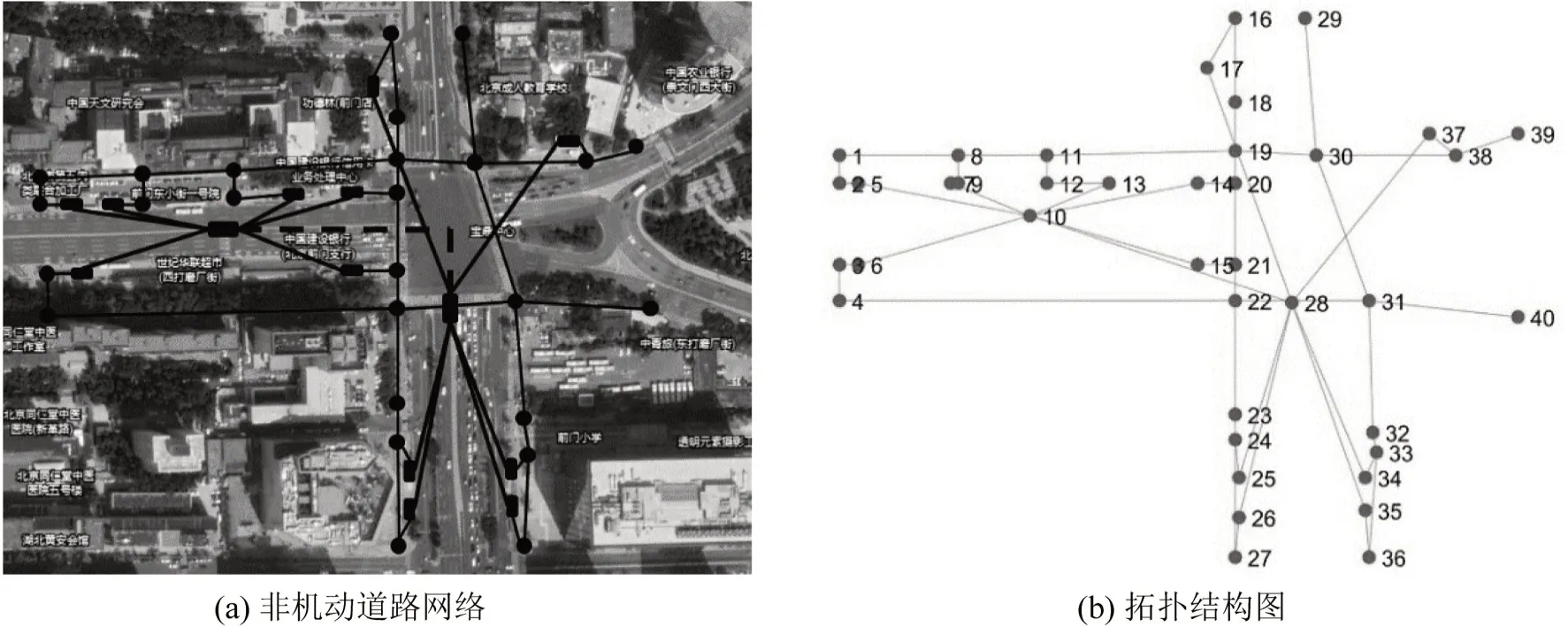
图7 非机动道路及其拓扑结构图Fig.7 Non-motorized road network and the corresponding topology

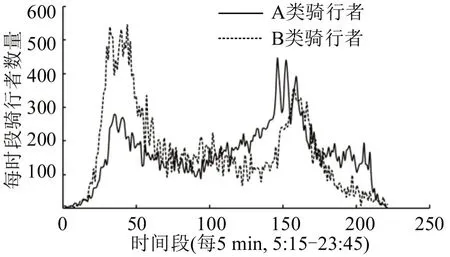
图8 各时段A类、B类骑行者数量Fig.8 Number of type-A and type-B riders in each period

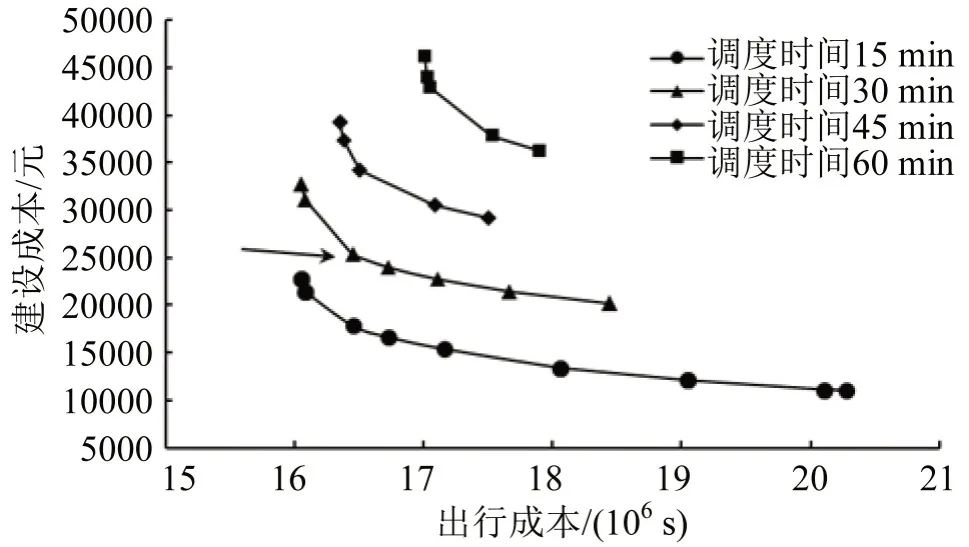
图9 不同调度时间下的帕累托解Fig.9 Pareto solution under different bike relocation time

3.3 混合交通流仿真与停车位布局规划

对图7中点22 对应的停放区进行停车位布局规划，图10为其周边区域道路拓扑图。

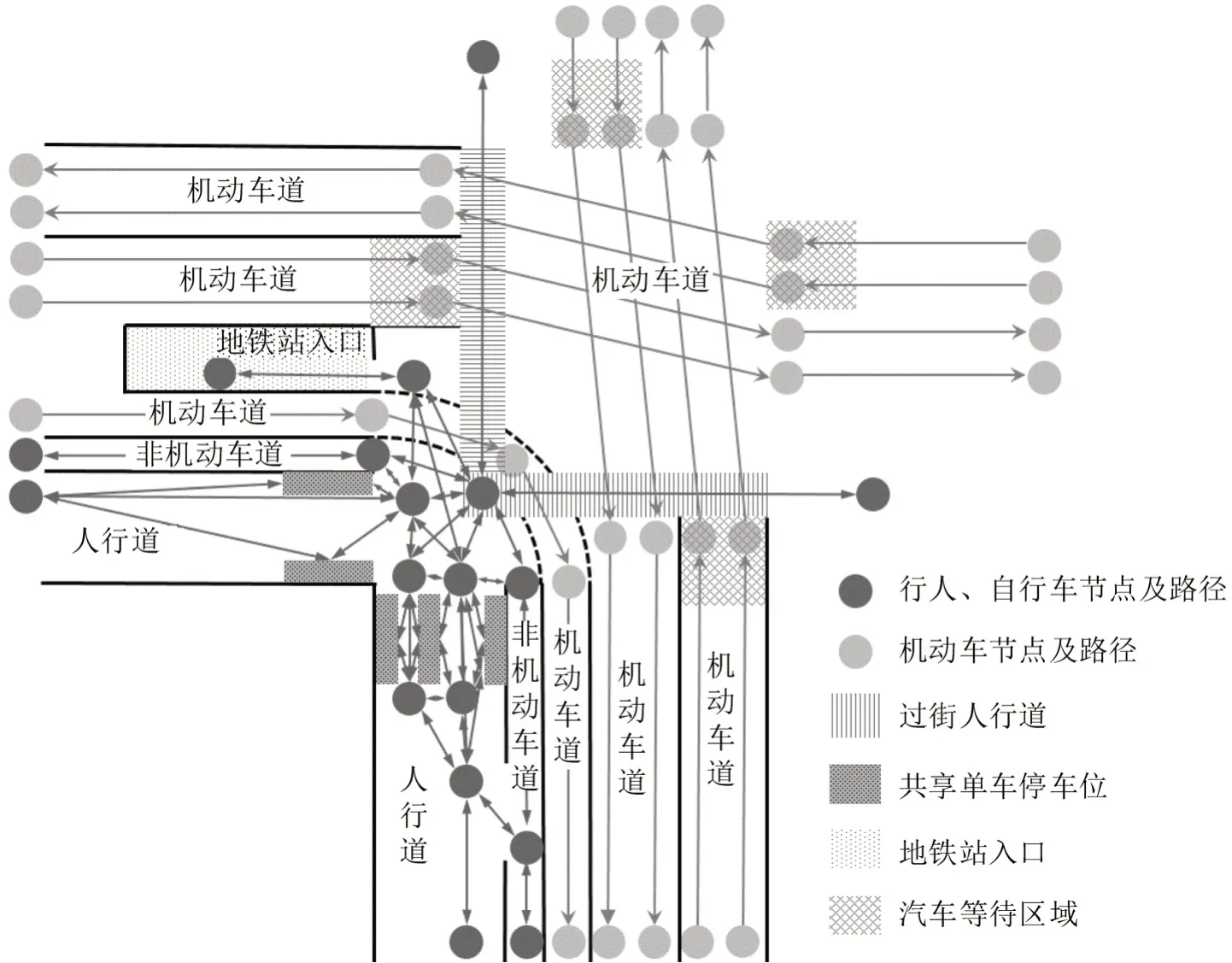
图10 混合交通流仿真场景设计Fig.10 Design of simulation scenario for mixed traffic condition

首先针对不同到达率，对图10场景进行多次仿真，整体通行时间和风险指数如图11和图12所示，其中各点为具体值，连线为平均值。仿真结果表明，通行时间和风险指数均随到达率提高而不断增加，且波动变大。本文随即以时间成本和风险指数和为目标，对具体停车位布局进行优化，结果如图13所示。其中，停车位更集中地接近A 类使用者的起点和B 类使用者的终点，与直观契合，因为骑行速度快，能提高通行效率。同时，停车位更靠近自行车道，并留出较多道路空间，有助于实现行人和自行车分离。

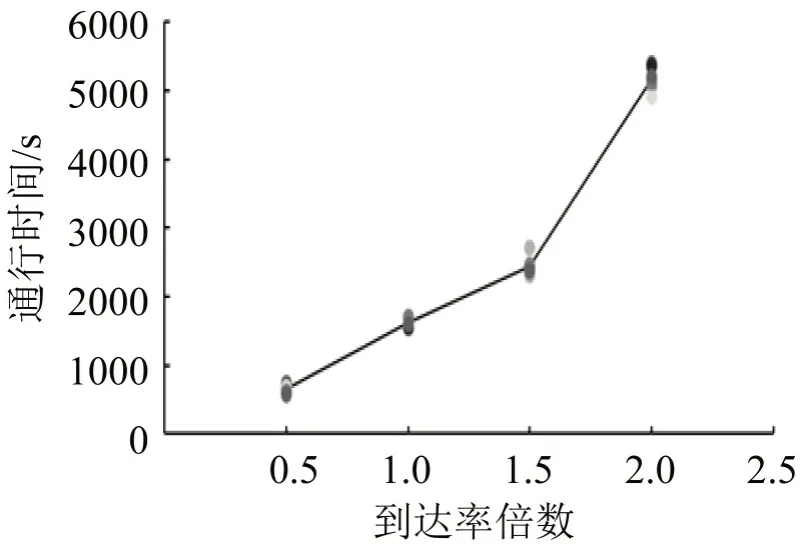
图11 不同到达率下整体通行时间Fig.11 Total traffic time under different arrival rate

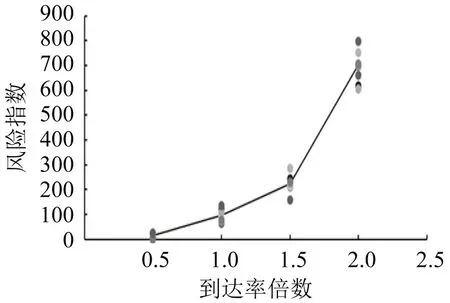
图12 不同到达率下整体风险指数Fig.12 Risk index under different arrival rate

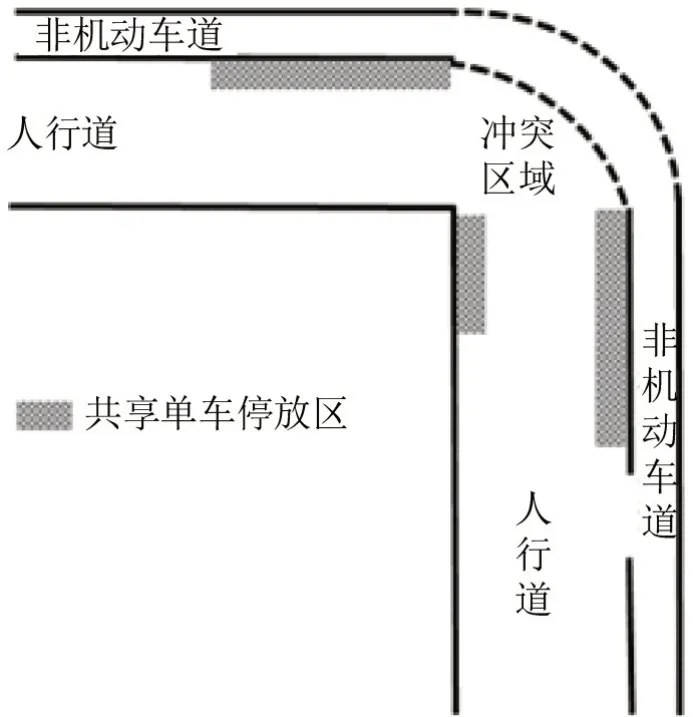
图13 共享单车停车位优化结果示意图Fig.13 Illustration of optimized parking spots layout

4 结论

本文针对共享单车停放区规划问题，在宏观层面利用DBSCAN和混合整数线性规划优化停放区选址和定容，微观层面利用混合交通流仿真和基于代理模型优化停车位布局。相比传统方法，宏观层面，研究基于共享单车订单数据和轨道客流刷卡数据等大数据，通过数据驱动方式，考虑共享单车使用者停放区选择模型和调度响应限制；微观层面，研究提出混合交通流仿真框架和评价指标，从而科学量化评价停车位布局影响。研究以北京市崇文门地铁站周边区域为例，验证方法有效性，并针对政府管理和停放区规划给出指导意见，包括共享单车调度时间要求；停放区选择以日常集中需求点为主，并根据停/取车需求差和调度要求确定容量大小；停放区应靠近建筑出入口位置，同时紧邻自行车道，并留出足够道路面积。