SS型与LCC型感应耦合电能传输系统的对比研究*

李逸杰， 苏建徽， 张 健， 汪海宁， 刘 硕

(合肥工业大学 电气与自动化工程学院，安徽 合肥 230009)

0 引 言

感应耦合电能传输(inductively coupled power transmission,ICPT)作为一种灵活、高效的新型电能接入技术，采用发送侧与接收侧分离的磁路机构，摆脱了传统电能传送直接电气连接的限制，因而受到越来越多的关注。目前已被广泛应用于各领域包括移动电话、电动汽车、植入式医疗设备和铁路运输等，具有良好的应用前景[1～4]。

评判ICPT系统的工作性能有多项指标，如有效传输距离，功率传输特性等[5,6]。文献[7]从谐振网络的电容电压、系统故障的鲁棒性、系统的最大传输功率三方面对LCC型与SS型ICPT系统进行了分析，并且指出两种补偿结构在这三项性能指标上各自的优势，然而该文对两者的效率传输性能却没有作出详细的分析与说明，故本文针对ICPT系统的效率传输特性对两种补偿拓扑进行进一步研究，得出了两者适用的负载电阻与互感的范围，为不同工况下ICPT系统补偿网络的选择提供了理论指导。

1 ICPT系统的工作分析

图1为SS和LCC补偿方式下系统的等效电路。其中L1和L2分别为发射侧线圈与接收侧线圈的自感量，M为两者之间的互感量，RP为发射线圈的内阻，RS为接收线圈的内阻。与SS型补偿网络相比，LCC型补偿网络在原(副)边增加了一个补偿电容Cf1(Cf2)与补偿电感Lf1(Lf2)，其与发送线圈,串联电容构成的谐振环节除了产生高频正弦信号的作用以外，还可以滤除能量变换环节中产生的高次谐波。

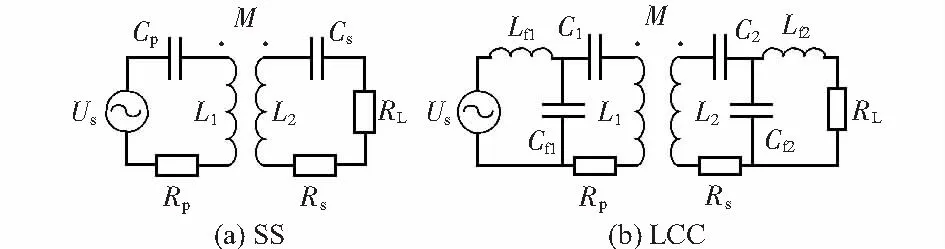
图1 SS型与LCC型ICPT系统的拓扑结构

定义系统副边的自阻抗为Zs，则当系统工作于调谐频率时两种补偿方式下对应的Zs分别为Zs,ss=RL+Rs与Zs,lcc=Lf2/Cf2RL+Rs，利用互感理论，可以得到副边电路折合到原边的反射阻抗

(1)

比较上述两种不同补偿方式下系统的反射阻抗可以发现，当系统工作于谐振状态时，两者的反射阻抗都呈纯阻性，但是在反射阻抗与负载电阻的关系上却形成了反差：如果暂时忽略接收端线圈的内阻值Rs，则LCC型补偿方式下系统反射阻抗的大小与负载电阻阻值呈现正比例关系，而SS型补偿方式下系统的反射阻抗则与负载电阻为反比例关系。在接下来的部分可以看到，两者的这种区别，直接导致了它们在效率传输特性上的不同。

2 两种补偿网络效率传输特性的对比分析

2.1 线圈偏移时效率的稳定性对比

在对两种补偿网络进行效率传输特性的分析之前，先求出两种ICPT系统的传输效率，可通过下式计算得到：(系统总效率=发射端效率接收端效率)，即：η=ηp×ηs=[Zref/(Zref+Rp)]·[(Zs-Rs)/Zs]。

由上式得到两种ICPT系统传输效率的表达式为

(2)

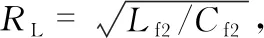
结合上述分析，考虑到两种补偿方式的恒流输出特性，所以在线圈偏移时传输效率的稳定性方面，SS型ICPT系统适用于功率较小的场合，而LCC型ICPT系统则更适用于功率较大的场合。

2.2 负载与互感对效率值的影响

由上一节得到，在不同负载电阻范围内，两种ICPT系统的传输效率在抗线圈偏移的稳定性上各具优势。然而，在各自优势负载范围内，两者的效率值谁更具有优势却不好直观判断，于是，利用作差法对两者进行进一步的比较：令δ=ηlcc-ηss,将式(2)代入并化简，得到

(3)

一般来说，LCC型ICPT系统中的补偿电感Lf1和Lf2为μH级别，而补偿电容Cf1和Cf2一般是nF级别，故接收端补偿电感与补偿电容的比值Lf2/Cf2大约在1 000左右，而线圈的内阻值则一般在0.1～1之间的范围内，故有：RpRs≪Lf2/Cf2；此外，在对耦合线圈进行设计时，为了保证较好的传输效率与传输功率，经常采用对称式结构的设计[8]，所以在此条件下，原副边线圈的形状结构、导体的材料、线圈的匝数等都是基本一致的，因此发射线圈与接收线圈的内阻值是比较接近的，即Rp/Rs≈1。

依据上述分析对式(3)作出进一步的化简

(4)

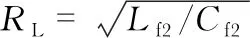
表1 两种拓扑结构效率值的对比

为了更加直观看出两种补偿方式下系统传输效率与负载电阻、互感的关系，取负载电阻在0～100 Ω之间变化 ，互感在0～100 μH 之间变化，对两种ICPT系统进行仿真分析，如图2所示。

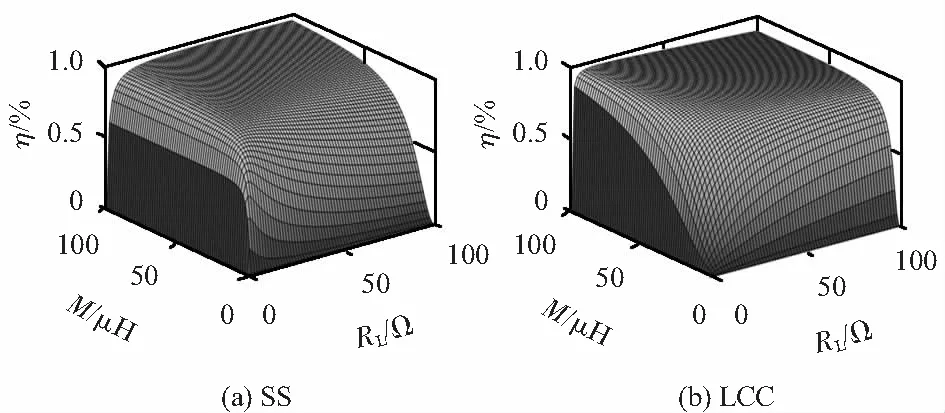
图2 两种补偿拓扑对应传输效率与互感、负载电阻之间的关系

由图2可以看出，仿真的对比结果与表1的推论比较吻合。并且从图中可以发现，当互感较小时，两种ICPT系统传输效率都处于较低的水平；随着互感的增大，整体效率曲线变得更加平滑稳定并且保持在较高的水平。由此可见，增大互感值对系统效率的提升有着积极的作用，但互感值的提升也意味着线圈体积的增大，损耗与成本也会随之增加，因此设计时需要兼顾多方面来考虑。

2.3 最高效率负载点与互感关系分析

在实际应用中，往往希望系统能够工作在最高效的状态，然而，当线圈发生偏移时，互感会随之变化，能够使效率达到最优的匹配负载点也会因此而发生改变，故下文将结合2.1节的推论，继续探讨两种ICPT系统的最高效率负载点与互感的关系。

对两种补偿网络条件下的系统传输效率η关于负载RL求偏导并令其等于零

(5)

解得当LCC型ICPT系统与SS型ICPT系统在传输效率达到最大时，最佳匹配负载的取值为

(6)

结合本文之前的分析，两种ICPT系统匹配的最佳负载处于各自的优势负载范围之内的取值为

(7)

于是解得能使两种ICPT系统最佳匹配负载工作在各自优势范围内的互感取值均为

(8)

依据2.2的分析对上式进行化简，最终得到

(9)

从上述计算结果可以看出，当互感小于该临界值时，两种ICPT系统效率达到最高时的最优负载点均位于各自优势的负载范围内，然而需要注意的是，对于SS型ICPT系统来说，其输入阻抗是随互感M的减小而不断减小的，在输入电压一定时，线圈偏移程度过大可能会导致输入端电流应力过大而造成危险，相比之下LCC型ICPT系统工作在此互感区域则更加安全。

3 实验验证

3.1 不同负载阻值下两种ICPT传输效率与互感的关系

为了验证两种补偿网络条件下系统效率传输特性对比分析理论的正确性，搭建了一个工作频率为100 kHz的感应耦合电能传输系统的实验平台，实验中各项元器件参数如表2所示。图3(a)是负载RL的取值分别为15,30,60 Ω时 SS与 LCC型ICPT系统效率随互感变化的曲线图。

表2 系统参数

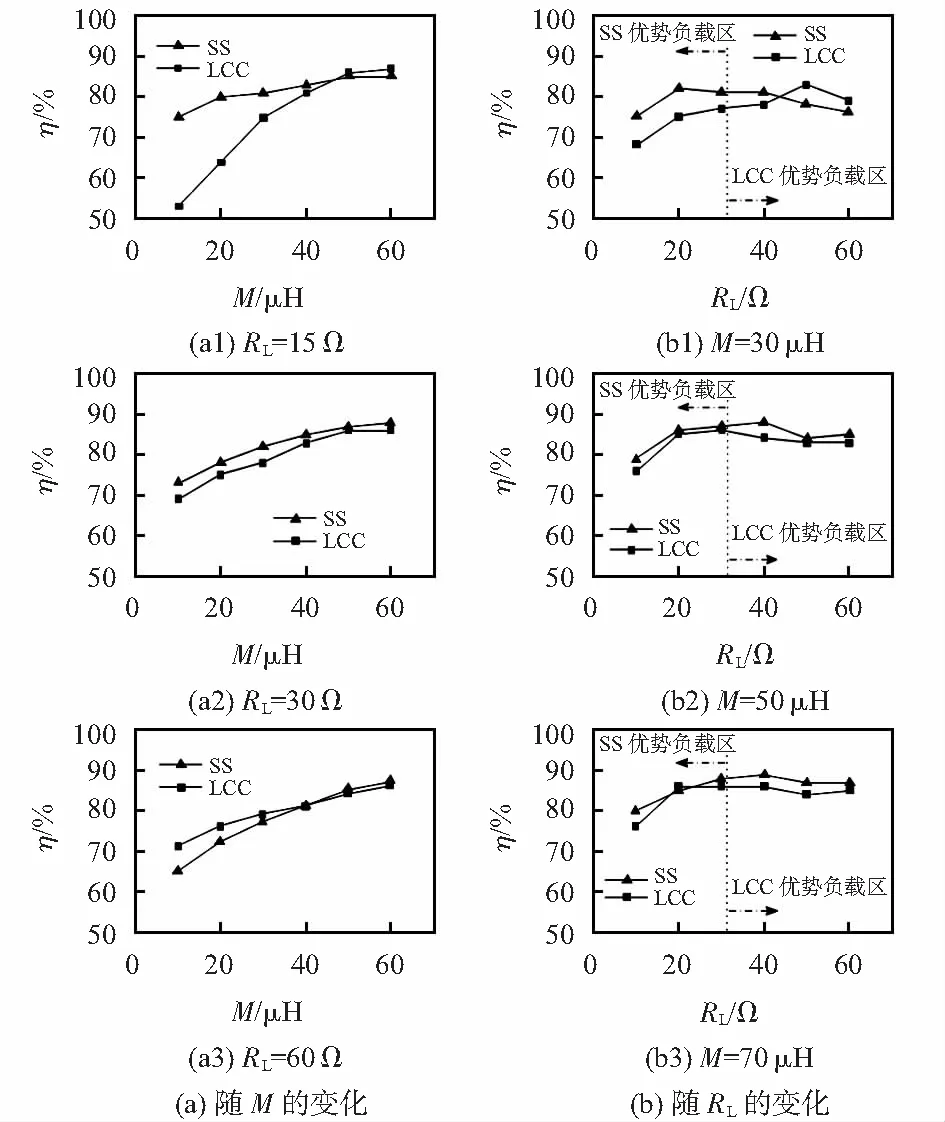
图3 两种拓扑结构传输效率变化曲线

对于表2所给定的参数，理论上使两种拓扑传输效率相等的互感临界值为50 μH，负载电阻的临界值为31 Ω。从图中实验结果可以看出，两者效率值的对比情况与之较为吻合。而在传输效率的稳定性方面，当负载电阻为15 Ω时，SS补偿方式下的传输效率在线圈偏移过程中(60～10 μH)下降了11.7 %，而LCC则下降了39.1 %，相比之下LCC补偿方式下对应的传输效率下降的幅度更大且趋势较为明显；当负载电阻为30 Ω时，线圈的偏移使SS与LCC的传输效率分别下降了17 %和19.7 %，两者下降幅度差距不大；当负载电阻为60 Ω时，两者效率下降的百分比分别为25 %和17.4 %，LCC补偿方式下的传输效率下降幅度更小但趋势并不明显。总的来看，实验结果比较好地验证了文中的理论分析。

3.2 最高效率负载点与互感关系验证

从图3(b)可以看出，在互感系数为30 μH即小于临界值的情况下，两种拓扑下传输效率取得最大值时的负载点均位于各自的优势负载范围内；当互感系数为50 μH即等于临界值时，两者的最高效率负载点在都在优势负载区的分界线附近；而在互感系数为70 μH即大于临界值的情况下，两者的最高效率负载点已经位于对方优势负载区内，这也验证了理论分析的正确性。

应该注意到，本文中实验结果与理论分析还是有一定差异的，主要的原因有以下3点：1)分析时忽略了LCC原副边补偿电感的内阻；2)有限的实验数据并不能完全体现出真正的效率最高负载点；3)理论分析的前提是假想系统处于理想的状态下，而实际的系统与理论分析是存在差异的。

4 结 论

针对感应耦合电能传输系统的效率传输特性，对SS型与LCC型ICPT系统展开对比研究。通过理论分析及实验验证，所得结果表明：在不同互感与负载电阻参数条件下，SS型与LCC型补偿拓扑结构在效率值及传输效率的稳定性上各自具有一定优势；当互感小于临界值时，两者的最高效率负载点均位于各自优势负载范围内。