新型围限颗粒介质联轴器持续剪切下的扭矩涨落行为

雷 刚 欧阳鸿武 喻海良,3 唐 昕

1.中南大学高性能复杂制造国家重点实验室，长沙，4100832.中南大学机电工程学院，长沙，4100833.中南大学轻合金研究院，长沙，410083

0 引言

对围限颗粒介质剪切后体积变化的研究一直都受到科研人员的高度关注，REYNOLDS[1]通过实验最先引入剪切膨胀概念。装满砂砾和水的柔性橡皮袋受挤压时，体积不但没有减小反而增大的现象被称为雷诺膨胀(即Reynolds dilatancy)[2]。雷诺膨胀是颗粒介质独特的物性之一，与涨落致有序定律、记忆效应、堵塞、滞后效应和棘轮效应等物理机制息息相关。BERNAL等[3-4]以硬球颗粒的随机致密堆积(random close packing，RCP)结构作为液体分子的结构模型，很好地描述了液体在熔点时的分子结构。SCOTT等[5]对圆筒内硬球颗粒的堆积问题进行了研究，利用实验验证了硬球颗粒的RCP结构的密度为0.637。HOWELL等[6]利用光弹效应将二维受剪颗粒介质的力链进行可视化，首次在实验过程中清晰地展示了颗粒受剪切作用时复杂的力链网络。BOBRYAKOV等[7]对石英砂剪切形成的螺旋滑移线族进行了实验再现，且在2017年由BLUMENFELD等[8]求得螺旋滑移线族的数值解。ZOU等[9]采用X射线断层成像技术表征颗粒状聚合物之间的连接，从而可靠地预测颗粒堆积的结构、密度和失效特性。因为颗粒介质固有的复杂物性，使得其实验研究一直都存在挑战[10]。

近年来，和圆筒围限硬球颗粒的堆积问题一样，剪切变形模式的内在机理及其复杂性也备受关注[11-12]。NICOLAS等[13]将硬球颗粒置入左右竖板分别与底板通过铰链连接的立方体容器中，当左右竖板在±Ω的角度范围内转动时，颗粒受到循环剪切作用，结果表明等剪切幅度致密化过程符合反对数定律，与振动致密过程相同。颗粒介质受剪作用时，将在介观尺度上形成织构，即所谓的力链，MAJMUDAR等[14]利用光弹圆盘进行实验并利用统计力学进行了细致分析，发现强力链和弱力链的存在会导致剪切作用时的各向异性。颗粒介质的状态和物性采用密度-载荷-温度的三维堵塞相图(LIU-NAGEL相图)来描述[15]。LUDING等[16]、KUMAR等[17]提出用一个被人们忽视的变量——堵塞密度φJ来描述颗粒系统变形的历史和作用方式(记忆效应)，研究表明，颗粒介质的膨胀、蠕变、应力弛豫和棘轮效应等特殊力学性能均与φJ有关。当颗粒受剪切作用时体积膨胀，堆积密度降低，剪切模量G≥0，系统应力p增大；当系统趋近平衡状态，剪切过程中颗粒介质不再膨胀，压力将趋于零并可能出现体积收缩。从膨胀到收缩，系统经历了一个临界转变，这个转变点所对应的密度就称之为堵塞密度φJ。BROWN等[18]设计的万能机械抓手正是利用了颗粒系统堵塞的特性：将颗粒介质(咖啡豆)装入橡胶袋中，在接触目标物体后减小橡胶袋中的压力从而使颗粒介质发生堵塞，变得坚固。由于颗粒介质具备柔性，这种万能机械抓手可以适应各种不同形状的物体，韩奉林等[19]也证明了利用颗粒介质的真空堵塞效应可以有效提高这种柔性机械抓手的极限承载能力。堵塞效应的理论研究和工程应用都表明，围限条件下硬球颗粒受剪切作用体积发生膨胀或收缩，都受到堵塞密度φJ的影响，这是因为当系统密度φ在φJ附近时，应变以及应力的符号将发生改变。应变εJ=ln(φ/φJ)，表示系统离(非)堵塞态“有多远”；应力p=BεJ，其中B≥0表示系统体模量，φJ控制着系统的内涨落，但目前如何利用实验测量LUDING等[16-17]在数值模拟中研究的φJ仍是一个悬而未决的问题。汽车传动系统的四驱化趋势日渐突显，中央差速器作为四驱技术的关键，如何提高差速器的性价比成为当前汽车工程领域中一个热点和难点问题。对围限颗粒介质联轴器扭矩传递特性开展实验研究，一方面可进一步提高对颗粒介质物性的表征能力，获取调控其力学响应的方式和途径(如对堵塞密度φJ的测量与控制)；另一方面可对现有黏性联轴器进行改造升级或更新换代，形成适用于四驱系统的新型围限颗粒介质联轴器技术原型机。

颗粒介质的相变行为与堵塞密度φJ出现临界转变相关，φJ能够反映外力的作用历史、方式和状态对力学响应的影响，因此，如何利用围限条件(剪切速率，压力，剪切幅度，颗粒数目、粒径等)对φJ进行调控，以期获得预期的颗粒介质堆积结构和稳定的力学性能，仍是一个热点和难点问题。本文利用硬球颗粒介质联轴器持续剪切实验，探明联轴器在不同剪切速率、初始法向应力和颗粒堆积厚度等条件下的扭矩传递特性，探讨了φJ与扭矩波动特性之间的联系，提供了一种可能的测量φJ的实验方法。

1 实验

1.1 联轴器结构与样品制备

为测试颗粒介质联轴器在不同围限条件下的力学响应特征，本文研制了围限颗粒介质联轴器装置(图1)。图1中，输出轴11既是壳体的一部分，也是输出扭矩的结构，输入轴2连接来自变速器的取力器或分动器的输出轴，而输出轴11与汽车后桥或前桥差速器连接。当输入轴2开始转动时，带动剪切盘10旋转，颗粒介质受到剪切作用后，在轴向上发生膨胀或收缩，加大或减小轴向推力，再通过摩擦片5、6将这种剪切膨胀或收缩效应进行“放大”，使联轴器传递的扭矩在小剪切作用下发生大响应。联轴器总扭矩T为摩擦片组之间的力矩T1和剪切盘与钢珠颗粒之间的摩擦力矩T2之和。

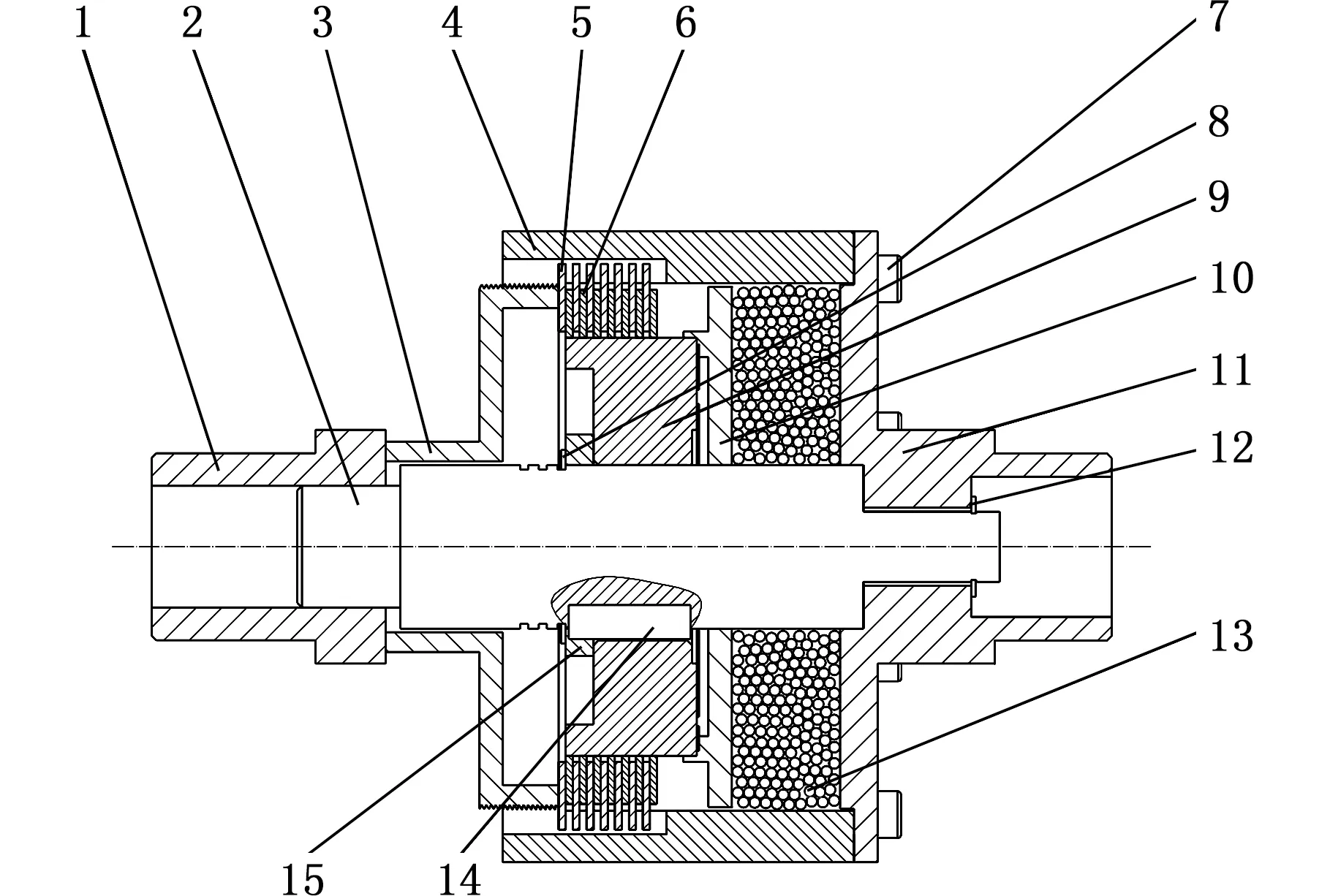
1.输入轴轴套 2.输入轴 3.螺纹盖 4.圆筒 5.外摩擦片6.内摩擦片 7.M6内六角螺栓 8.φ35弹性挡圈 9.外齿10.剪切盘 11.输出轴 12.φ15弹性挡圈 13.钢珠颗粒14.平键 15.垫圈图1 颗粒介质联轴器示意图Fig.1 Schematic of granular media coupling

颗粒介质在圆筒中的堆积如图2所示。钢珠颗粒在联轴器中堆积区域的形状为圆环形柱体，内径35 mm，外径112 mm，最小堆积厚度为25.6 mm。开始测试前，将粒径分别为2，3，4 mm的钢珠颗粒按70%、21%和9%的比例混合，并通过搅拌、轻微摇晃、振动和抚平等操作使颗粒介质随机堆积在联轴器底部的空腔中，使其初始厚度为27 mm，钢珠(GCr15)密度为7.83 g/cm3，此厚度下颗粒介质总质量为1113.85 g，因此初始填充率Vn/Ve=(1113.85/7.83)/{27π[(112/2)2-(35/2)2]×10-3}≈0.593(Vn、Ve分别为颗粒填充体积和空腔体积)，如图2a所示。

(a)在联轴器壳体中填充钢珠颗粒 (b)多分散颗粒堆积照片(c)剪切面结构 图2 颗粒介质在圆筒内的堆积Fig.2 The packing of granular media in the cylinder

摩擦片组采用摩托车离合器中的干式摩擦片，这种摩擦片由金属摩擦材料制成，具有耐磨损、超高硬度等特点。外摩擦片内圆半径R1=45 mm，内摩擦片外圆半径R2=56 mm。此外，剪切盘的剪切面(即与钢珠颗粒接触的下表面)为平面，如图2c所示，其内径、外径分别为35 mm、112 mm。

1.2 测试系统

实验系统由计算机、302型扭转实验台(torsion testing machine-302， TTM-302)以及围限颗粒介质联轴器组成(图3)，其中，TTM-302扭矩测量范围为±300 N·m，测量误差为0.5%，转速范围为±2 r/min。该实验系统适用于慢速转动工况。输出轴11与TTM-302固定轴连接，输入轴2通过左端的轴套与其动轴固连从而实现转动，并通过外齿带动内摩擦片6和剪切盘10旋转，螺纹盖3可与第一片外摩擦片6接触，从而对内部摩擦副施加一定的初始法向应力σ0，联轴器扭矩T可通过TTM-302测量得到。

图3 扭转实验系统Fig.3 The torsion testing system

1.3 实验参数

实验中需确定颗粒介质的剪切速率n、初始法向应力σ0以及颗粒堆积厚度h等参数，其中σ0计算公式推导如下。

实验中螺纹盖采用的螺纹螺距p=1 mm。由机械原理可知，扭力扳手力矩M等于螺旋副间的摩擦阻力矩M1和螺纹盖与外摩擦片间的摩擦阻力矩M2之和：

M=M1+M2

(1)

(2)

(3)

将式(2)和式(3)代入式(1)，得

(4)

其中，F0为螺纹盖对整个系统内施加的法向压力；螺纹盖细牙外螺纹的公称直径D=113 mm；螺纹升角ψ=1°42′；螺纹中径D2=0.9D；螺旋副的当量摩擦角φv=arctan(1.155μv)；螺纹盖的内径d=102 mm≈0.9D；螺纹盖与外摩擦片间的摩擦因数μc=0.15。

将各参数值代入式(4)，整理后得F0的计算公式为

(5)

则装置内部的初始法向应力为

(6)

式中，S为名义剪切面面积。

以剪切速率n、初始法向应力σ0以及颗粒堆积厚度h为实验变量分别进行研究，单次实验时长t=100 s，实验主要参数见表1。

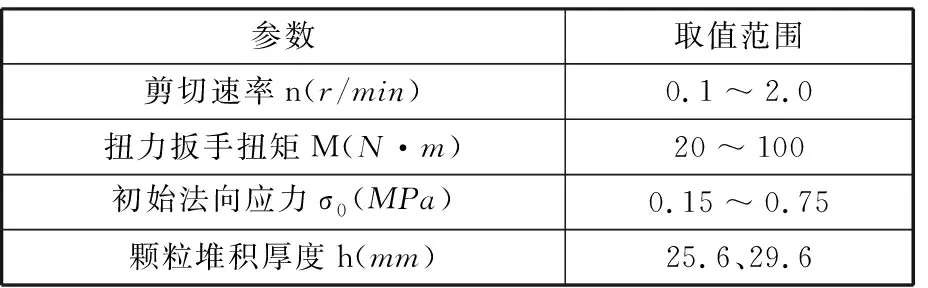
表1 参数取值范围

2 结果

2.1 扭矩的涨落特性

从持续剪切实验结果中可以发现，总体上扭矩T在传递过程中在某一扭矩值附近波动(图4a)。从图4b中三个不同阶段的放大图能够更加清晰地看到，扭矩曲线具有不断涨落的行为，并且不同阶段扭矩波动特征具有明显差异。b阶段中ΔT有小幅增大，c阶段中箭头标识处，T的波动周期不变，但在此处ΔT的大小发生了突变，从d阶段中可以看到T的波峰具有高-低间歇式变化(高：实心点，低：空心点)的特点，由此可以看出，ΔT随时间t变化，即扭矩的涨落是一个与过程和历史相关的物理量。

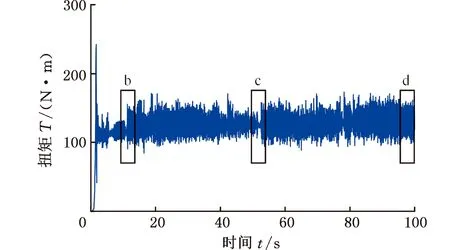
(a)n=0.5 r/min、σ0=0.375 MPa时扭矩波动

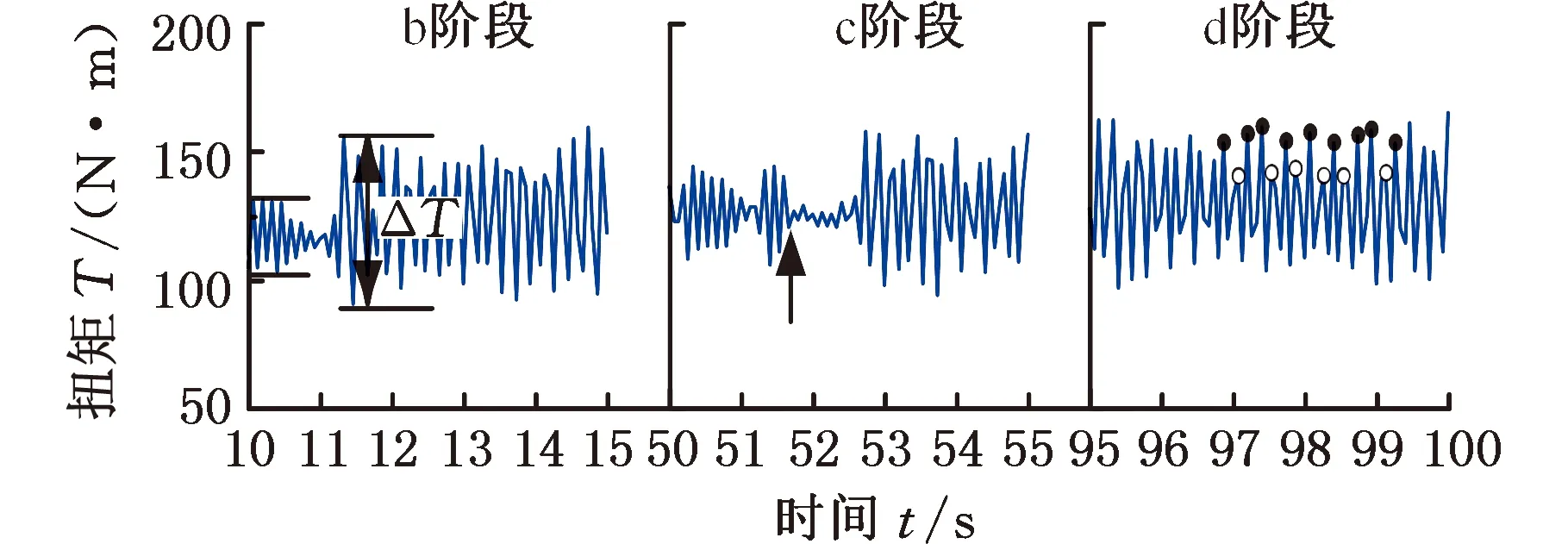
(b)图4a三个阶段的放大图图4 扭矩T随时间t的波动Fig.4 Fluctuation of torque T with time t

笔者假设ΔT的变化能够间接反映颗粒介质几何堆积结构和力网结构的演化，而作为状态变量的堵塞密度φJ能够表征颗粒介质这种演化历史并产生“记忆”。在剪切过程中，颗粒介质膨胀还是收缩是个令人困扰的问题，当引入φJ之后，情况就发生了根本转变。如果在堵塞态颗粒的堆积密度高于堵塞密度情况下进行剪切，颗粒介质必然发生膨胀，堆积密度降低；当密度降低至堵塞密度后，系统开始收缩，同时，随着系统堆积结构和力网结构的演化又形成了新的φJ(即产生新的“记忆”)。由此，φJ就记录了颗粒介质的变形历史和状态，φJ的变化对应于颗粒介质内部结构的演化行为，它与扭矩T的关系推导过程如下。

围限颗粒介质联轴器的总扭矩T为摩擦片组之间的力扭T1和剪切盘与钢珠颗粒之间的摩擦力矩T2之和：

T=T1+T2

(7)

(8)

(9)

其中，μp为摩擦片间的摩擦因数，取μp=0.4；μs为剪切盘与钢珠颗粒之间的摩擦因数，取μs=0.5[2]；z为摩擦副对数，z=5；R1为外摩擦片内圆半径；R2为内摩擦片外圆半径，R2=56 mm；r1为剪切盘内圆半径，r1=17.5 mm;r2为剪切盘外圆半径，r2=R2=56 mm；σ为系统内受到的法向应力，由于颗粒介质受剪切作用时体积应变会发生变化，假设其体积应变的变化量为Δε，弹性模量为E，则有σ=σ0+EΔε。

将式(8)、式(9)和以上参数值代入式(7)，则总扭矩

T=169.41π(σ0+EΔε)

(10)

因此，内外摩擦片有助于更加清晰地体现颗粒介质的剪切变形对联轴器扭矩传递特性的影响。

颗粒堆积密度φ与系统内法向应力σ的关系由Heckel’s规则[2]确定：

(11)

式中，K、C为与颗粒介质物性相关的常数，可由实验确定。

根据σ计算公式，将式(10)代入式(11)，得

(12)

假设颗粒介质堆积密度φ与堵塞密度φJ的关系为

φ=φJ+Δφ=φJ+α/Δε

(13)

其中，α为与围限结构尺寸相关的比例常数。实际上，这里的Δφ可用来表征离堵塞状态“多远”变形过程中堆积密度的变化是围绕着φJ这一本质变量进行的，同时通过φJ也将密度与屈服或堵塞这种状态的变化联系起来。

将式(13)代入式(12)，得φJ与扭矩的关系：

T=169.41π{ln[1-(φJ+α/Δε)]-1-C}/K

(14)

容器的几何尺寸以及剪切速率一旦确定，则式(14)中的堵塞密度φJ作为颗粒系统内在的状态参数亦即确定下来。系统通过结构上的变化即体积应变的变化量Δε来达到特定条件下的平衡状态。Δε的符号可以表征颗粒系统的体积到底是发生膨胀还是收缩：当Δε为正，体积发生膨胀，此时ΔT亦为正，T将会增大；反之，当Δε为负，体积收缩，ΔT亦为负，T随之减小。因此，颗粒介质的几何堆积结构与力学响应相互耦合。

随着剪切速率n的逐渐增大，扭矩传递特性也随之发生变化，经过傅里叶变换得到振幅-频率图(图5)。从图5中可以发现，存在临界剪切速率nc=0.8 r/min，当nnc时，系统不再有显著的周期性，力学响应相对平缓，无明显冲击，颗粒剪切膨胀-收缩的幅度明显下降。

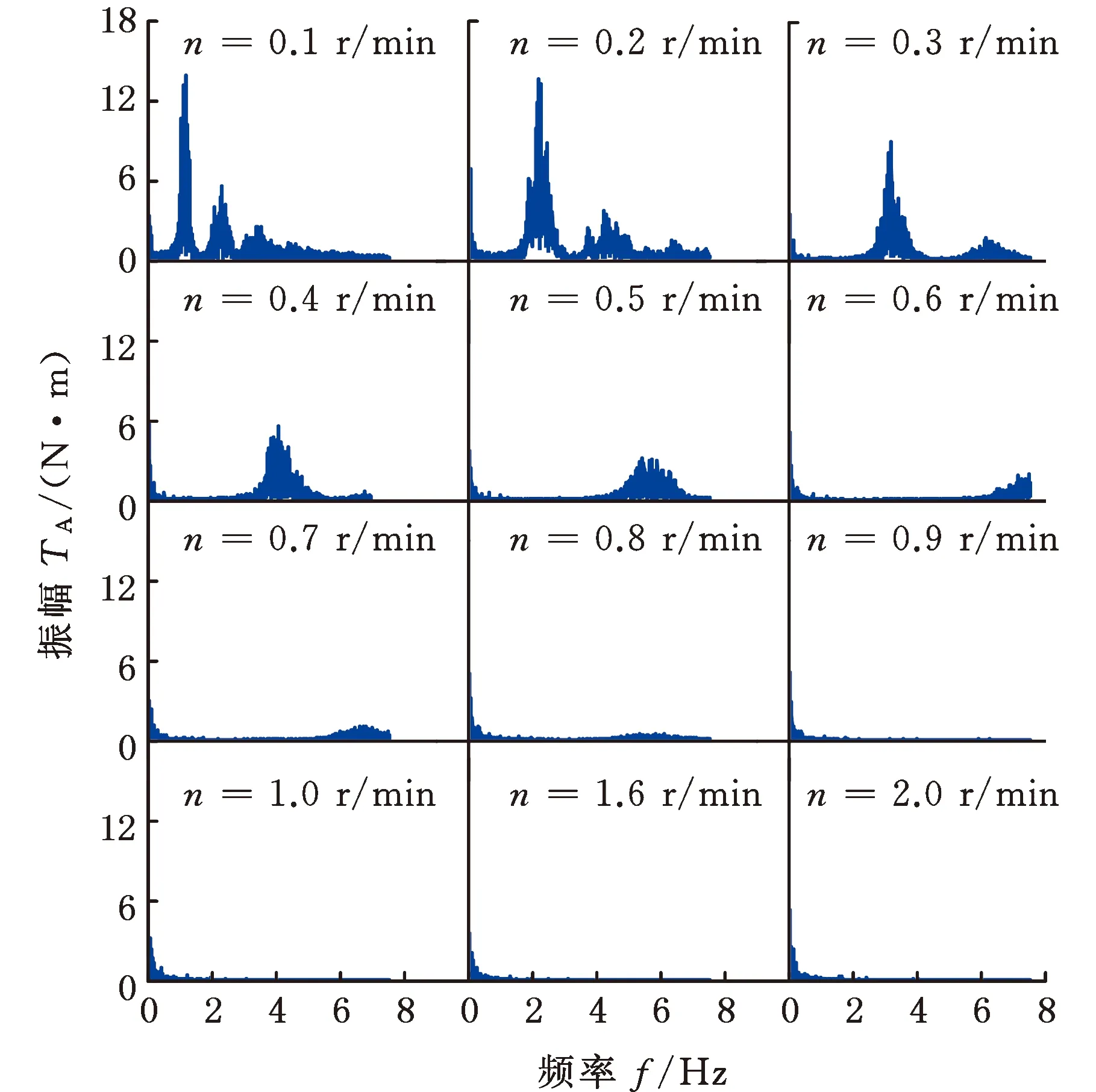
图5 扭矩在不同剪切速率下的傅里叶变换Fig.5 Fourier transform of torque at differentshear speeds

在很低的剪切速率下(n=0.1 r/min，图5)，对扭矩曲线进行傅里叶变换后，发现在此条件下系统中存在四个特征频率，分别为f(1)=0.017 Hz，f(2)=1.126 Hz，f(3)=2.247 Hz以及f(4)=3.379 Hz，结合图4可以看出f(2)为基频(即扭矩曲线波动频率)，且存在关系f(3)≈2f(2)，f(4)≈3f(2)。在很低的速率下，颗粒离散特性明显，受剪时力链历经形成-断裂-重构的循环过程，在力链断裂时，颗粒组元存在坍塌行为，而f(3)和f(4)这两个特征频率恰恰反映了力链从断裂到重构的频率大小，具体来说，长度较长的力链，其断裂-重构的频率为f(3)，而长度较短的力链，其断裂-重构的频率则为f(4)。最低频率f(1)=0.017 Hz则表征了颗粒介质在剪切过程中缓慢的蠕变行为，在低速和高速剪切下，这种行为都会存在。在剪切速率处于中高速(n=0.9～2.0 r/min)时，傅里叶变换图中只存在一个很低的频率，不超过1 Hz。高速剪切时，可将颗粒系统视为一个块体，它与剪切盘之间处于界面摩擦状态，摩擦过程相对比较平顺，不涉及内部力链的断裂-重构过程，因而不会出现较高的特征频率。

2.2 剪切速率对扭矩传递的影响

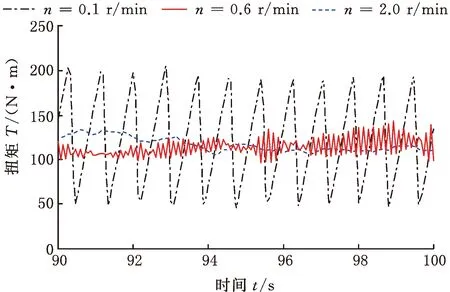
(a)三种剪切速率下扭矩涨落

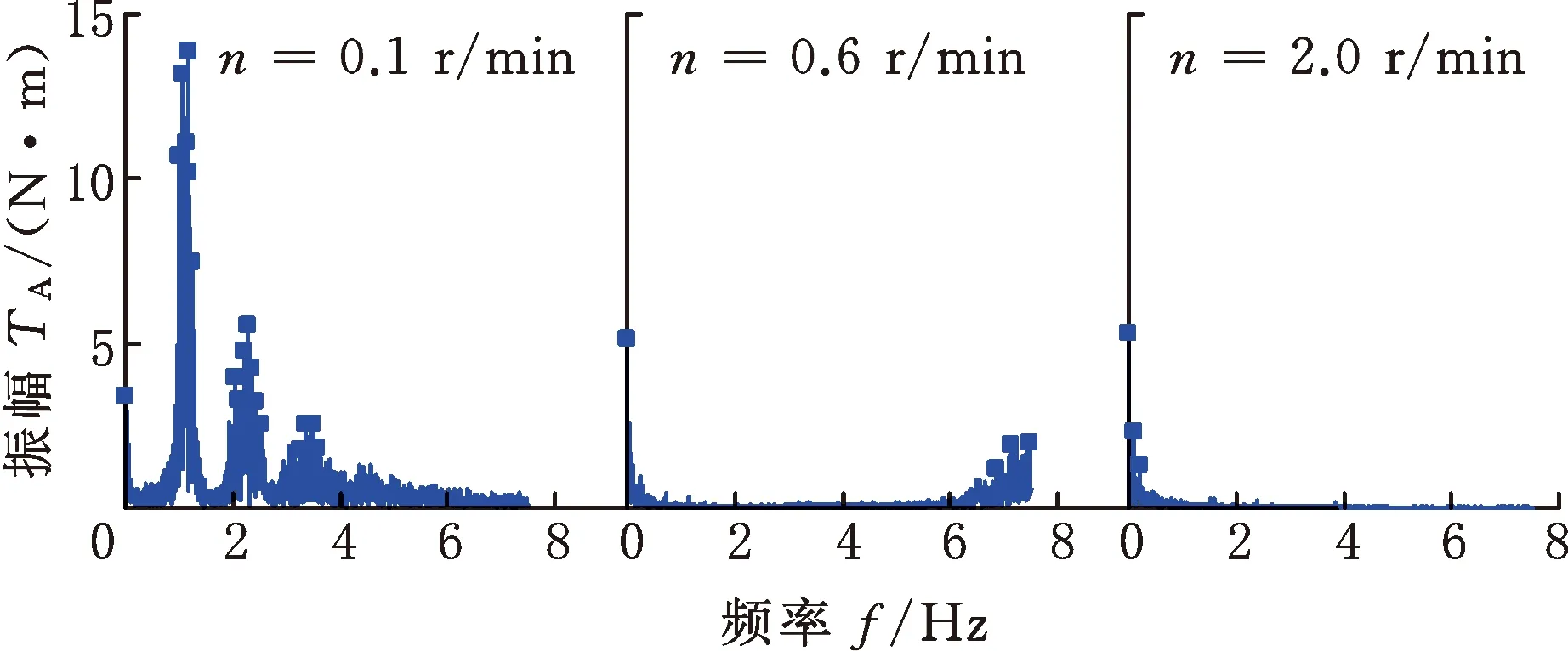
(b)傅里叶变换图6 三种剪切速率下扭矩涨落及其傅里叶变换的比较Fig.6 Comparison of torque fluctuation and Fouriertransform at three shear speeds

当初始法向应力σ0=0.375 MPa，剪切速率n=0.1，0.6，2.0 r/min，实验时间段Δt取90～100 s时，扭矩传递特性如图6所示。从图6a中可以看出，速率越低，扭矩的间歇式响应越明显，呈现出脉动特性，而速率越高，扭矩的传递过程越平顺，此时表现出连续式响应特征，即剪切速率显著影响颗粒剪切膨胀-收缩的幅度。从图6中还可以发现，扭矩在脉动过程中始终存在一个均值Tm，当n=0.1，0.6，2.0 r/min时，Tm分别为120.57，109.72，105.75 N·m。

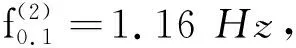
图6a中，n=0.1，0.6 r/min时颗粒系统表现出一种坍塌行为，这种行为在颗粒组元相互作用的无序系统受外力作用而屈服时发生。如果这种无序比相互作用的阻碍影响更大，那么系统的失稳是由很多小的单个失稳而造成的，如果相互作用强于无序，系统就会出现一次大的失稳。

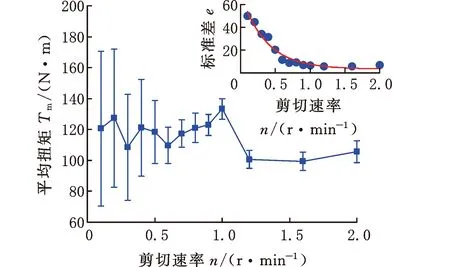
(a)σ0=0.375 MPa

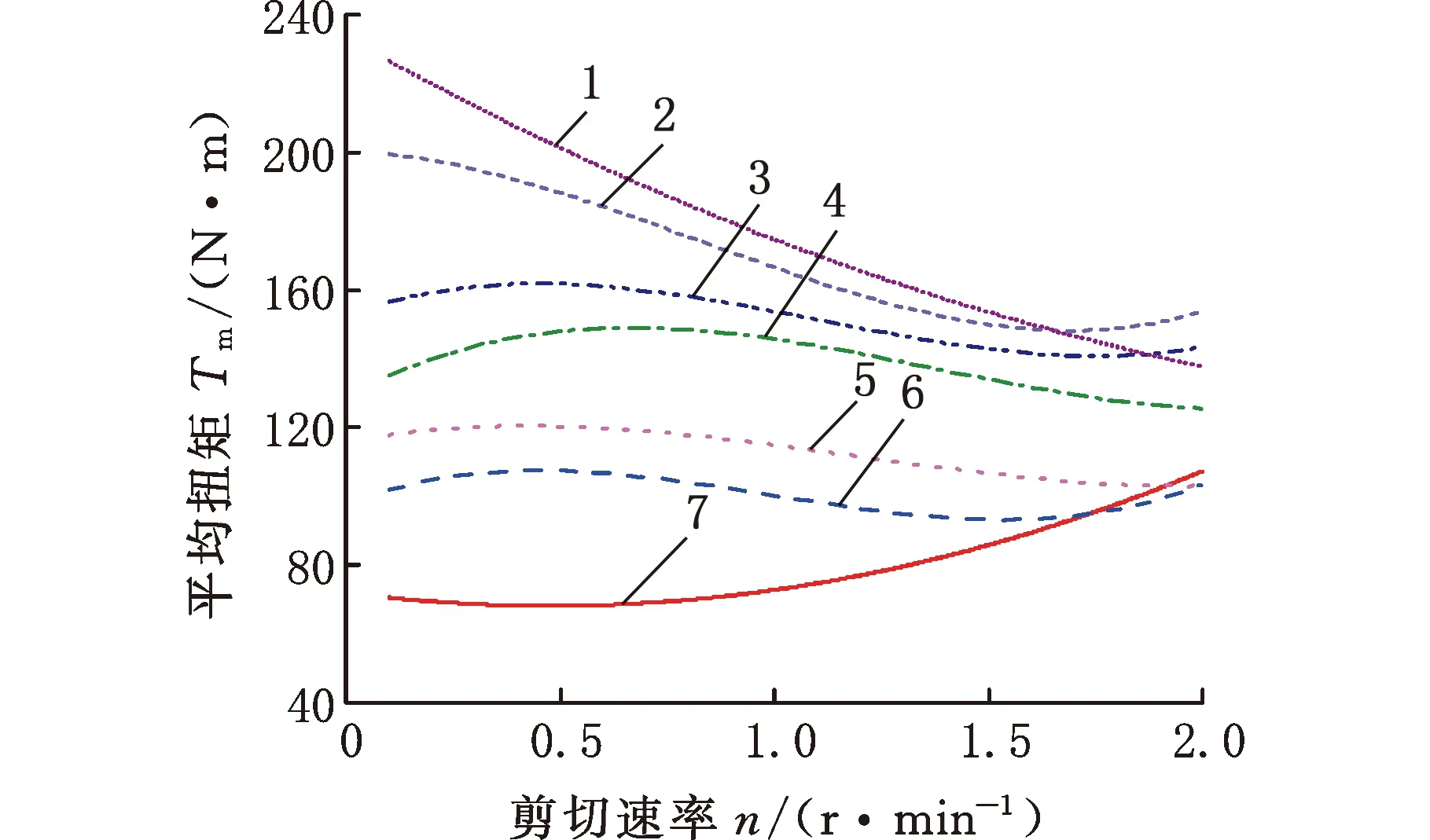
1.σ0=0.750 MPa 2.σ0=0.675 MPa 3.σ0=0.600 MPa4.σ0=0.525 MPa 5.σ0=0.375 MPa 6.σ0=0.300 MPa7.σ0=0.150 MPa(b)σ0取0.150～0.750 MPa图7 扭矩与剪切速率的关系Fig.7 Relationship between torque and shear speed

图7给出了剪切速率对扭矩特性的影响规律，在n=1.0 r/min时，Tm发生了转折，图7a中右上角的嵌入图即为标准差的变化曲线，拟合关系为e=3.43+66.64exp(-n/0.36)。从图7b中的曲线可以看出，随着初始法向应力σ0的增大，相同n下的Tm总体上也会增大，另一个明显的特征是，σ0较小时，n越大，Tm也随之越大，但是当σ0较大时，情况则相反，n越大，Tm则越小，由此可见，扭矩与剪切速率之间具有非线性关系。

2.3 初始法向应力的影响

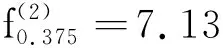
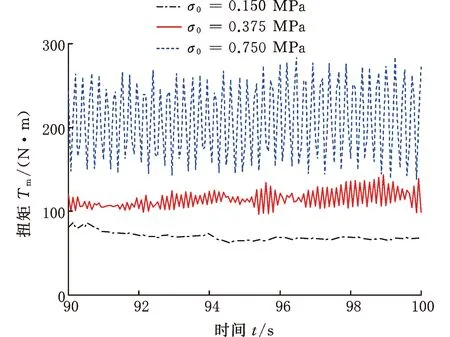
(a)不同初始法向应力下扭矩传递特性

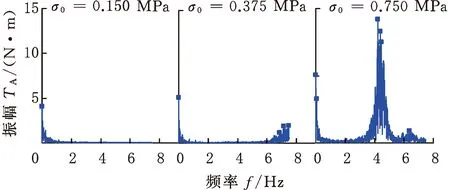
(b)傅里叶变换图8 不同初始法向应力下扭矩传递特性及其傅里叶变换Fig.8 Torque transfer characteristics and Fouriertransform under different initial normal stresses

图9所示为初始法向应力对扭矩特性的影响规律。从图9a中的嵌入图可以看出，拟合后得到的转变点σ0=0.384 MPa。由于剪切应力等于法向应力与摩擦因数的乘积，所以扭矩和初始法向应力之间基本成线性关系(图9b)，并且存在2个转变应力点，即σ1=0.25 MPa和σ2=0.6 MPa。当初始法向应力σ0小于0.25 MPa时，随着剪切速率的增大，颗粒系统在环剪作用下发生膨胀，扭矩随之增大，σ0高于0.6 MPa时，系统体积逐渐收缩，扭矩减小，当0.25 MPa <σ0<0.6 MPa时，两种状态交替出现，这种独特现象在剪切堵塞相图中得到了解释[20]。

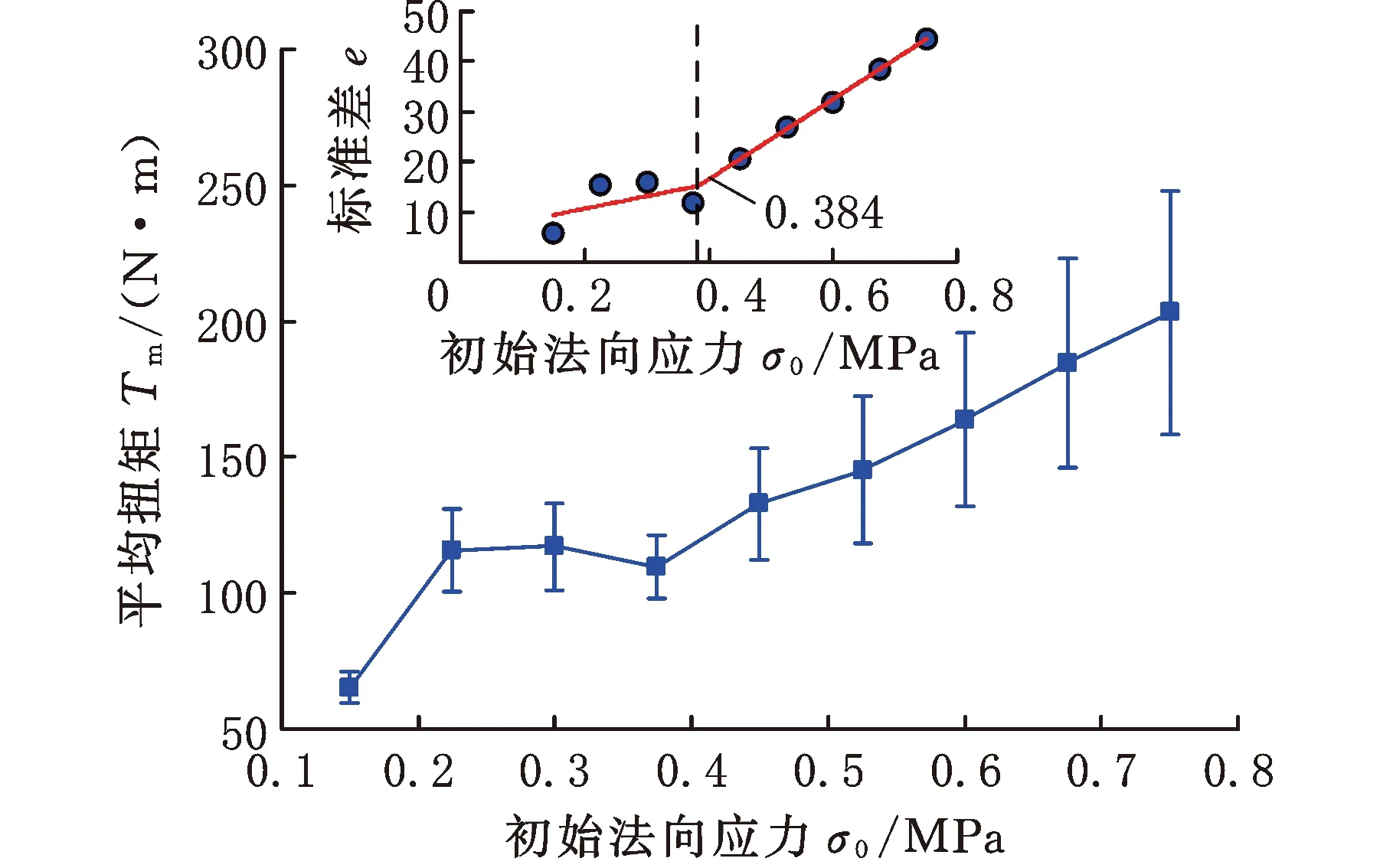
(a)n=0.6 r/min

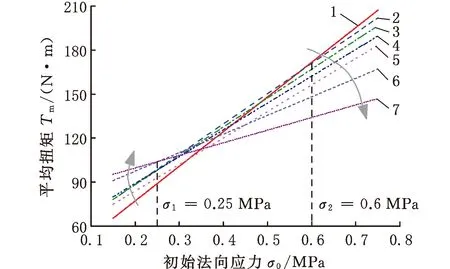
1.n=0.1 r/min 2.n=0.3 r/min 3.n=0.5 r/min4.n=0.6 r/min 5.n=0.9 r/min 6.n=1.0 r/min7.n=2.0 r/min(b)n取0.1～2.0 r/min图9 扭矩与初始法向应力的关系Fig.9 The relationship between torque and initialnormal stress

图9a中的嵌入图为扭矩值的标准差随初始法向应力的变化特征，两者满足如下关系式：

2.4 颗粒堆积厚度

实验还发现颗粒的堆积厚度h也会对扭矩传递性能产生影响，如图10所示。在剪切速率n=2.0 r/min，初始法向应力σ0=0.375 MPa的条件下，选定堆积厚度h分别为25.6和29.6 mm的颗粒样本进行实验。从图10中可以看出，当h=25.6 mm时，扭矩稳定后的均值Tm=94.98 N·m，当h=29.6 mm时，扭矩稳定后的均值Tm=110.34 N·m，即当厚度增加15.6%时，扭矩均值可增大16.2%。

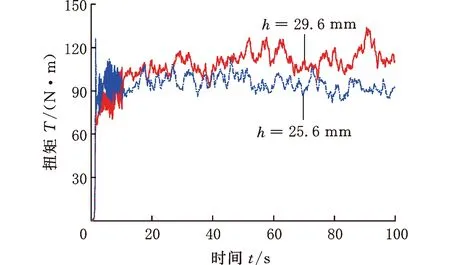
图10 堆积厚度对扭矩的影响Fig.10 Effect of packing height on torque

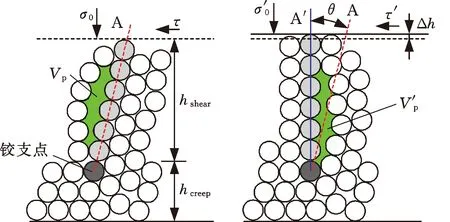
(a)剪切前的初始态(b)剪切后强力链发生旋转(膨胀态)

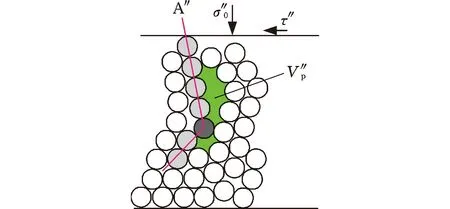
(c)继续剪切则强力链折叠(收缩态)图11 剪切膨胀的介观结构演化机制：强力链撑杆模型Fig.11 Mesoscopic structure evolution mechanism ofshear dilation: the strong force chain strut model

强力链撑杆模型可以合理地解释这种厚度效应。如图11所示，颗粒介质受剪时(剪应力为τ)，从作用力表面到6～7层颗粒单元区域(剪切层厚度hshear)处于快速剪切状态，导致各向异性的力链形成(用浅灰色颗粒表示)，而剩下的颗粒团簇(蠕变层厚度hcreep)作为基底颗粒提供支撑，处于慢速蠕变状态，力链拥有各向同性，强弱差别不大。厚度增加，剪切层厚度hshear变化不大，蠕变层厚度hcreep增加明显，从而各向同性力链成分增加，致使基底变形难度较大，剪切层强力链不易断裂，屈服强度更大，从而使剪应力变大(τ′>τ)，扭矩增大。

3 讨论

3.1 非线性现象

图7b和图9b中存在的非线性现象符合剪切堵塞相图中的描述[20]，见图12，图中，Jammed表示堵塞态，Unjammed表示非堵塞态，SJ表示剪切堵塞态，F表示脆性态，φS表示发生剪切堵塞的最低密度，图中3个箭头代表三种不同法向围限应力条件，箭头所指方向为剪切速率增大方向。当法向围限应力σ0小于σ1时，颗粒在剪切作用下随剪切速率的增大而发生膨胀(箭头1)，堆积密度减小，最终小于堵塞密度φJ；当法向围限应力大于σ2时，随着剪切速率的增大颗粒发生收缩(箭头2)，穿越φJ线，从各向异性的剪切堵塞过渡到各向同性的堵塞状态；法向围限应力在σ1与σ2之间时，处于剪切膨胀-收缩波动状态(箭头3)，可能会多次穿过φJ线，并且箭头方向也可能向下(图中用虚线箭头表示)。这时扭矩呈增大趋势还是减小趋势取决于σ0更接近σ1还是σ2，σ0越接近σ1，颗粒出现先膨胀再收缩的特点，但总体上具有膨胀趋势，扭矩随之增大；σ0越接近σ2，颗粒存在剪切收缩的总体趋势，扭矩逐渐减小。

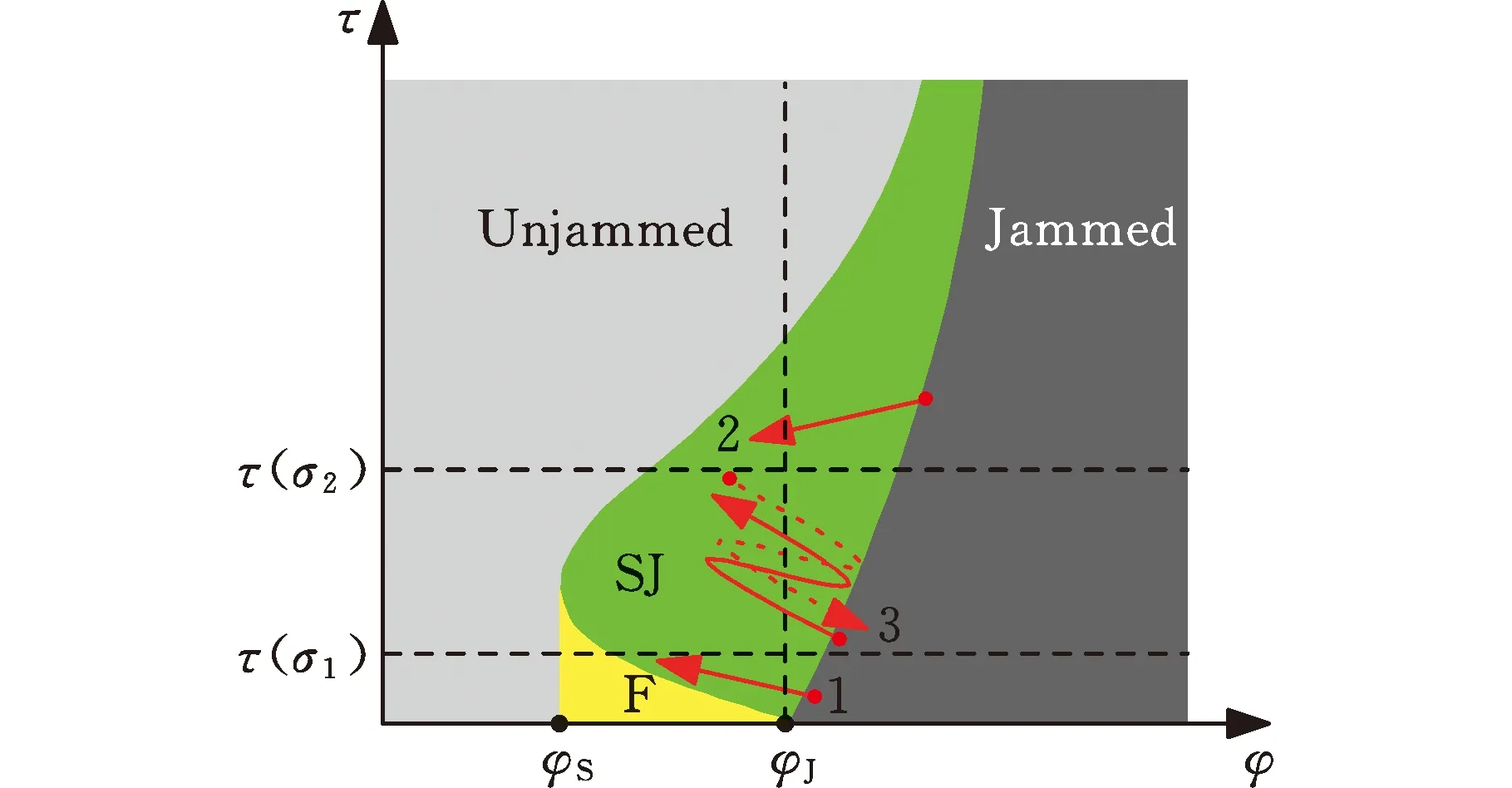
图12 剪切堵塞相图中的膨胀-收缩机制Fig.12 Dilation-compaction mechanism in shearjamming phase diagram

3.2 扭矩涨落机制

颗粒介质系统不同于连续介质，其宏观动力学行为是每个粒子共同作用的结果，在研究颗粒介质时有一种直接的理想化方法——将其视为一些结构单元(如弹簧、阻尼和梁等)的集合[21]。笔者将这种粒子间的相互接触理想化为弹簧和阻尼的集合(图13)，并使用这种动力学约化模型解释剪切过程中扭矩的涨落机制。初始法向应力σ0、剪切应力τ为施加在系统上的外力，粒子间的主要参数是等效刚度Keff和阻尼系数Q。

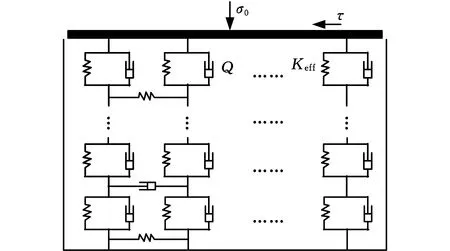
图13 颗粒系统动力学约化模型Fig.13 Dynamic reduction model of granular system

当颗粒系统处于黏着状态时，颗粒进入堵塞态，并储蓄剪切能；产生滑移时，颗粒介质中的摩擦耗散起到阻碍运动的作用，与此同时，系统的应力水平逐步降低。这样一来，颗粒尺度上的位移ΔX和时间Δt的统计值提供了屈服阶段的流变行为。颗粒介质的阻尼系数Q和屈服持续时间〈Δt〉均与堆积密度相关。依据文献[22-23]，颗粒动力学行为服从阻尼驱动谐振子方程：

(15)

当强力链在(颗粒与颗粒间、颗粒与剪切盘间)摩擦力的作用下绕铰支点(图11中黑色颗粒)发生旋转时，强力链从位置A到A′的旋转角为θ，引起的高度变化为Δh，且Δh是粒径d、强力链旋转角θ的函数，即Δh(d,θ)，见图11b。继续剪切过程，强力链发生折叠(图11c)，剪切层厚度hshear迅速减小，颗粒介质发生大规模坍塌。运动员在跳高时撑杆的受力情况都历经了锚定-弯曲-旋转的三个阶段。堵塞密度就对应颗粒介质的某个状态，此状态就决定了颗粒介质的力学响应特征。颗粒介质的力学特性在宏观上保持动态平衡，这是介观尺度上孔隙消失和生成达成平衡的结果，在平衡状态下，颗粒受剪切作用时的孔隙体积之和为一常数，因此Vp+V′p+V″p为一常数。

剪切过程中，当摩擦力小于颗粒介质的屈服应力时，颗粒介质在边界产生滑动失稳但没有明显的塑性变形；局部失稳时，即摩擦力大于屈服应力时，颗粒力链折叠并且相邻颗粒重排，如图11c所示。局部失稳的频率取决于颗粒的堆积密度，表现出剪切转变区(shear transformation zone，STZ)的重排行为特征，此时系统内多处发生局域塑性事件，并且导致应力急剧减小[24]。当堆积密度较低时，颗粒系统在剪切作用下通常能够找到新的能量最低状态(亚稳态)，这种状态通过STZ的重排方式可以实现。堆积密度较高时，由于力网几何结构的限制，颗粒系统更难在附近找到有效的构型，缺乏STZ形式的颗粒重排。存在一个临界堆积密度φc，当φ≫φc时，弹性模式转变为塑性模式，颗粒系统变形困难，而容易在边界位置失稳从而滑移。滑移累积到一定程度，导致力链旋转-折叠，而系统总是与外力平衡的趋势使几何结构和内部应力场发生变化，换言之，强非线性、远平衡态的颗粒介质系统逐渐趋于特定条件下的平衡态时，系统的体积和应力都会发生涨落。

4 结论

(1)持续剪切实验证实了存在LUDING等[16-17]利用仿真研究的堵塞密度φJ，当颗粒系统受剪时，堆积密度在φJ上下波动，利用颗粒介质堆积结构与力学响应相互耦合的特性可以间接测量φJ。

(2)可对φJ进行控制从而调节联轴器扭矩的涨落特性。控制φJ的方法有：改变剪切速率、初始法向应力、堆积厚度等。采用其他类型颗粒介质体系、剪切减薄或剪切增厚软物质调控扭矩传递特性的效果有待进一步的研究。