基于非等间隔采样的曲轴连杆颈测量技术研究

顾亭亭 楼佩煌 钱晓明

1.南京航空航天大学机电学院，南京，2100162.南京航空航天大学金城学院，南京，211156

0 引言

曲轴作为汽车发动机的核心部件，对发动机的性能有重要影响。曲轴主轴颈和曲轴连杆颈的加工精度评价技术和形位公差精密测量技术作为曲轴制造过程中的重要环节，对保证曲轴的加工质量至关重要[1-4]，引起了汽车工业界的关注。

国外对汽车发动机曲轴检测技术研究较早，从20世纪60年代便展开对曲轴测量机的研究制造，截止目前已出现许多测量精度高的检测方法和完善的检测设备，如德国HOMMEL和Dr.Heinrich Schneider、意大利MARPOSS、美国ADCOLE等公司[5-8]。德国HOMMEL公司开发的接触式曲轴综合测量设备用于曲轴终检环节，可以完成主轴颈和连杆颈直径尺寸的分级打标和自动分选功能，测量精度达到2 μm[9-10]。德国Dr.Heinrich Schneider公司开发的SKM系列曲轴测量系统采用的是复合测量方式，结合接触式位移传感器和面阵CCD(charge coupled device)可以分别完成接触式和非接触式测量，根据被测对象的不同特征选择合适的测量方法，以获取更多的测量数据进而提高测量精度，曲轴轴颈的直径测量误差可以控制在2 μm以内[11]。意大利MARPOSS公司开发的M2016、M110等产品运用了基于电感感应测头的曲轴测量方法，可以实现工件的自动上料、定位和旋转，除了测量功能外，该产品还具有零件分选、无损检测等功能。该公司开发的另一款Optoquickset曲轴测量机采用线阵CCD采集曲轴轮廓特征，安装多个超高分辨率的线阵CCD，曲轴旋转时可以测量曲轴全方位的轮廓数据，直径尺寸测量分辨力达到0.1 μm，测量误差在2 μm内，长度尺寸测量的分辨力在0.5 μm以内，测量误差在(6+l/200)μm以内[12-15]，其中，l为测量时的位移量。美国ADCOLE公司研发的Adcole 1200型圆柱坐标测量机(CCMM)是一种高精度测量仪，用于测量凸轮轴、曲轴和其他具有严格零件公差的圆柱形零件。该设备采用先进的激光干涉仪测量技术，拥有一个平面度极高的激光测量参考系统，提供精确的径向测量和长度测量，测量误差小于0.5 μm[16]。

国内的曲轴自动化检测技术起步较晚，总体上还处于探索阶段。田应仲等[17]针对曲轴连杆颈加工过程中的非圆磨削提出在线跟踪测量方法，但测量过程中受磨屑和金属屑的影响，测量精准度欠佳。邓杨[18]采用气浮拖板对非对称轴类零件进行测量，气浮拖板可上下运动，拖板上的测头做水平跟随运动，经过标定和误差分离后，曲轴四根连杆颈的圆度误差重复精度在0.2 μm内，圆柱度误差重复精度在 0.3 μm内，与美国ADCOLE公司的ADCOLE 1200SH检测结果进行对比，连杆颈的圆度、圆柱度、同轴度误差评定的偏差分别在 0.3 μm、0.5 μm、0.8 μm 范围内，但是此测量系统在单一时间内只能对单个轴颈进行测量。俞红祥等[19-20]利用V形基准块实现了连杆颈圆度准在线测量，采用的圆度测量方法是以测头扫描角度为基准的等间隔采样方式，相等采样间隔下获取轴颈表面整圈轮廓数据，信号处理后分离出圆度误差并进行数据修正，补偿后连杆颈圆度加工误差小于2 μm。上海交通大学开发了背光影像式曲轴沟槽自动精密检测仪器，通过随动精密控制系统驱动CCD摄像机、远心镜头及背光平行光源等组成的光学系统，检测曲轴沟槽的关键特征尺寸，研究了高质量图像的获取和处理方法，并对测量系统的机械结构进行了误差分析，通过对图像轮廓提取算法的改进以及对机械系统的误差补偿，提高了背光影像测量方法的测量精度、可靠性和稳定性，这种背光影像测量方法对测量环境要求较高，工作量较大[21-23]。李靖[24]设计了一种基于PLC的自动曲轴测量仪，该仪器运用伺服电机驱动曲轴回转，将PLC作为下位机控制运动系统，将光栅尺作为传感器采集轴颈轮廓数据，最后利用最小二乘法得到圆度、同轴度等形位公差。该测量方法采用高精度传感器对曲轴进行接触式高精度测量，但主轴颈和连杆颈是分开测量的，效率较低。

综上所述，国内的曲轴检测设备技术成熟度低，与国外先进技术和装备相比还存在差距。本文在接触式曲轴轴颈同步测量方法的基础上对连杆颈圆轮廓的测量展开研究。首先，根据曲轴的结构特点设计了一种多测头测量方法，在曲轴回转一周时完成对曲轴所有主轴颈和连杆颈圆轮廓的测量。然后，针对连杆颈测量过程中采样角度分布不均匀的问题，根据采样角度实际分布情况计算每个采样角对应的权函数，利用高斯滤波得到修正后的圆轮廓，解决非等间隔样本数据处理问题。最后，将该测量方法与三坐标测量仪对同一根曲轴的测量结果进行对比，验证了此测量方法的可行性和准确性。

1 轴颈同步测量过程中测头分布

1.1 轴向测头分布

曲轴轴颈同步测量方案是在一次装夹下对主轴颈和连杆颈进行同步测量[25]，在轴颈的轴向和径向均布置多测头的方法。测量时测头与主轴颈及连杆颈的圆周表面接触，曲轴旋转一周就既可以测量出主轴颈的表面轮廓数据，也可以采集连杆颈表面完整一周的轮廓数据。多测头的机械结构相对简单，对环境的适应性较高、抗干扰能力强，可以消除加工误差、安装及装夹误差，可用于误差分离。

被测曲轴的轮廓和测点分布如图1所示，其中，J1～J5为主轴颈，P1～P4为连杆颈。测量过程中，主轴颈J1～J5做绕回转轴线的自转运动，连杆颈P1～P4做绕回转轴线的圆周运动。轴向上每个轴颈分布两组测头，一次回转运动即可完成曲轴各轴颈的直径、圆度、圆柱度及同轴度等参数的计算。这种方法实现了曲轴多轴颈多参数的同步测量，缩短了检测时长，并且消除了重复装夹误差和测头移动误差。

1.2 径向测头分布

各个轴颈径向上也采用多测头分布，测头分布如图2所示，在轴颈的圆周上均匀布置m个测头，且测头杆指向圆心，即两侧测头连线经过曲轴各轴颈中心，可完成对被测曲轴所有轴颈径向尺寸相对校准件径向尺寸差值的同步采样。每个测头分别独立测量圆周轮廓ρn(n=1,2,…,m)，共获取m组数据，那么最终测量数据为m个测头的平均值，即

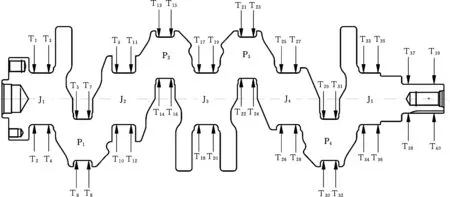
图1 曲轴截面及轴向测头分布Fig.1 Section and axial probe arrangement of crankshaft

(1)

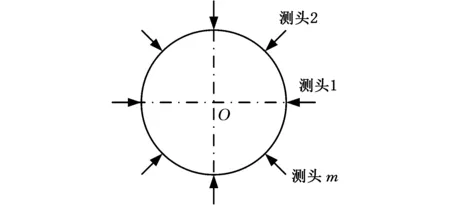
图2 径向多测头原理图Fig.2 Radial multi-probe principle diagram

每两个相邻测头之间的角度为

(2)

测量时测头与轴颈表面接触，曲轴围绕回转轴线旋转一周，根据相对运动，任何一个测头都是沿着轴颈表面移动的，并且可以沿轴颈表面旋转测量一周，所以测头的测量结果都是周期性的，并且满足狄利克雷条件，因此任何一个测头的测量结果都可以写成傅里叶三角级数的谐波总和，即

(3)

δn=δ1+(n-1)β

(4)

式中，e0为直流分量；i为谐波的阶数；ei为第i个谐波的幅度；φi为第i个谐波的初始相位；δn为第n个测头的位置角。

将式(4)代入式(3)，得到谐波总和与第一个测头位置角的函数关系如下：

(5)

可以推导出m个测头的测量误差为

(6)

通过使用多测头测量技术，可以将i次谐波误差与测量误差分离开来，而其他谐波误差均可消除。

2 连杆颈同步随动测量

2.1 连杆颈同步测量的实现

主轴颈做回转运动的同时，连杆颈做绕回转中心的圆周运动，为实现曲轴主轴颈与连杆颈的同步测量，使测量机构跟随连杆颈运动完成截面径向数据的采集，且不与主轴颈测量结构发生干扰,模拟发动机运转时连杆的运动状态，将曲轴的曲柄臂看作曲柄，连杆颈与测头部分看作铰链，将测臂看作连杆，设置滑块和铰链，设计一种曲柄摇杆式测量机构，机构原理如图3所示。其中，O是主轴颈中心，O1是连杆颈中心，OO1是曲柄臂，O1B是测臂，测头A安装在与测臂垂直的方向上，导轨B固定于升降管上，导轨B下降至测量点时与主轴颈中心距离为L，测臂O1B是可伸缩结构，随连杆颈的回转运动伸缩。

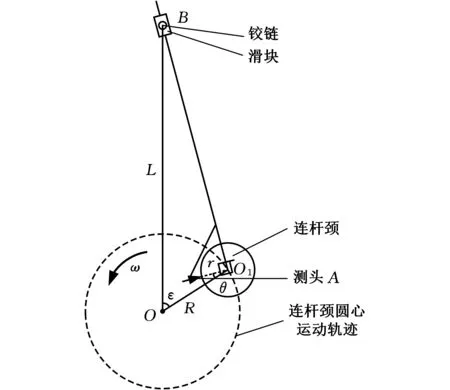
图3 连杆颈测量机构原理图Fig.3 Principle diagram of connecting rod journalmeasuring mechanism

图3中圆心O是回转中心，圆形虚线是连杆颈圆心O1的运动轨迹，虚线圆的半径R是曲轴的曲柄臂长度，连杆颈的半径是r，曲柄臂OO1与垂直升降台OB的夹角为ε。设曲轴测量过程中以逆时针方向为正，角速度为ω，设连杆颈上测头A与OO1的夹角为θ，根据ΔOO1B的余弦定理，测头A与曲柄臂OO1的夹角θ在曲轴旋转过程中关于主轴颈运动角ε的函数关系为

θ=

(7)

测头与曲柄臂夹角θ和主轴颈运动角ε的函数关系如图4所示，其中逆时针方向代表正方向，顺时针方向代表负方向，主轴颈旋转一周，ε由0°～360°变化过程中，θ相对于曲柄臂的角度由-90°变化到270°。由此可知,在主轴颈绕回转中心旋转一周的过程中，测头在被测连杆颈圆周表面扫描一周并采集连杆颈径向尺寸变化量。但是发现夹角θ与主轴颈运动角ε之间并非为线性关系，对夹角θ求导，得到其角速度与主轴颈运动角ε的关系曲线如图5所示。由图5可知，测头在连杆颈圆周表面的运动并非为匀速运动，这样导致采样间隔不相等，即采样角的分布在整个运动过程中是非等间隔的。

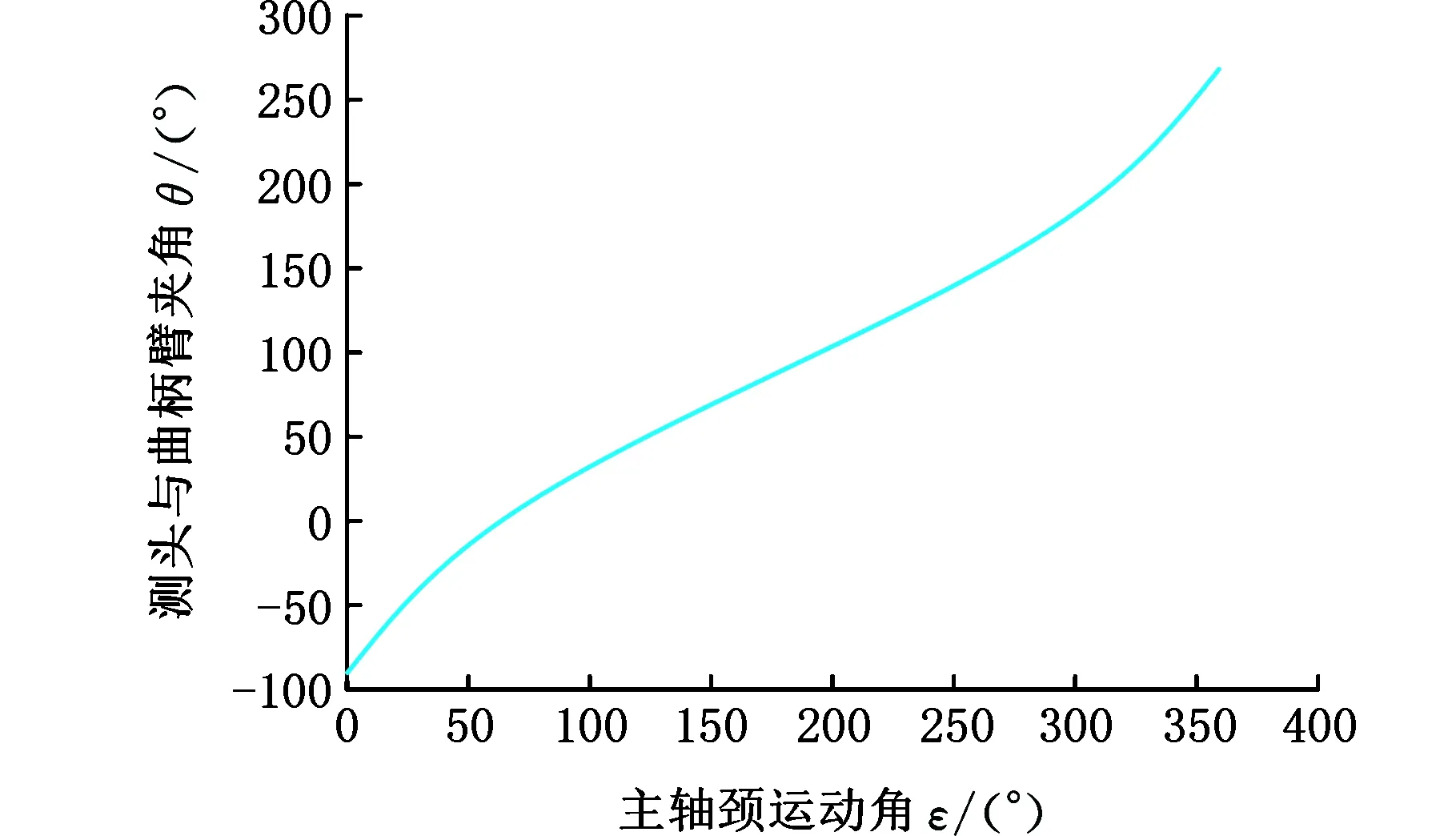
图4 夹角θ与运动角ε的关系曲线Fig.4 Relationship between θ and rotation angle ε

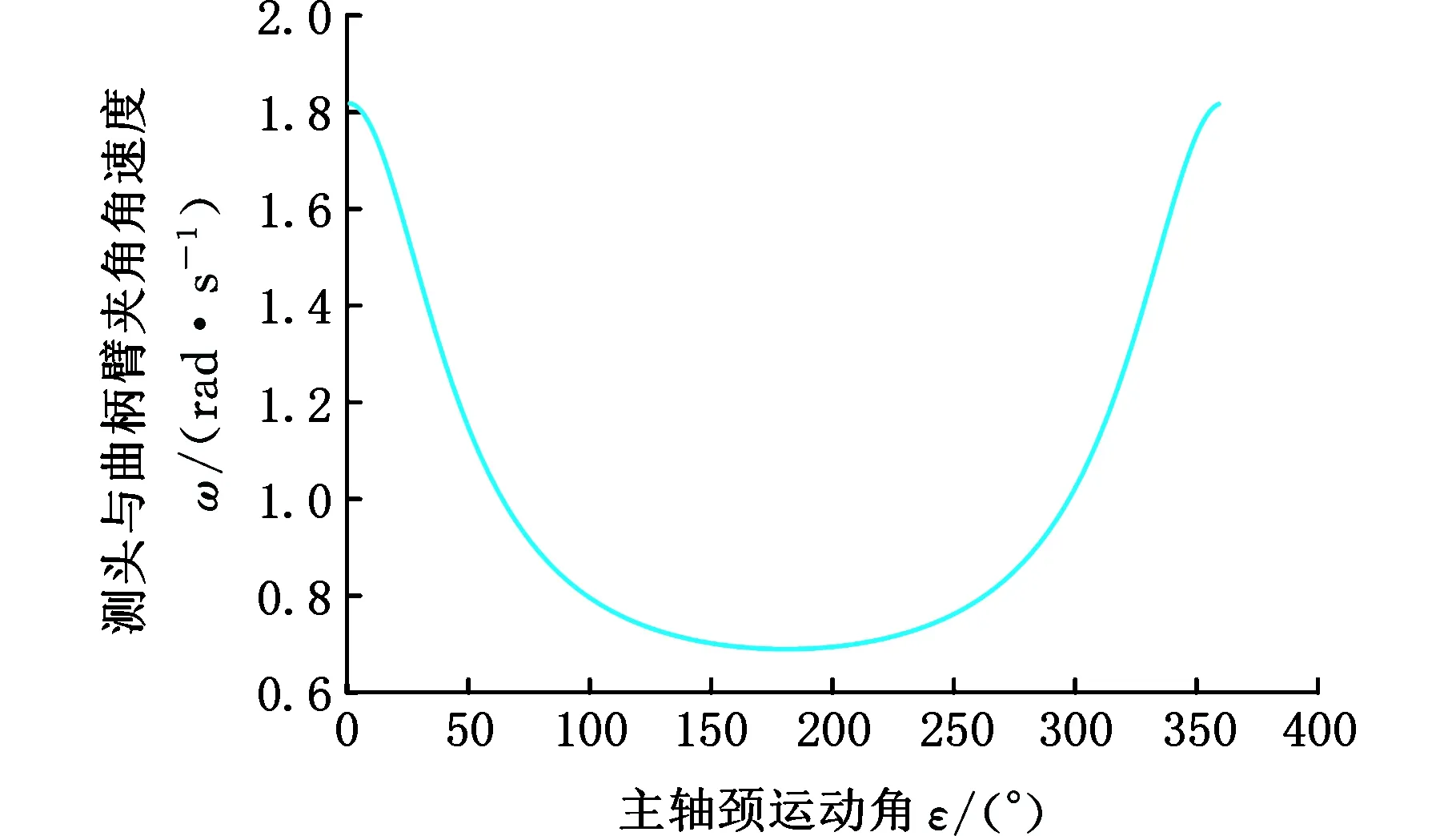
图5 夹角角速度ω与运动角ε的关系曲线Fig.5 Relationship between angular velocity ω androtation angle ε

2.2 非等间隔采样处理

测量过程中，曲轴围绕回转中心匀速旋转，即ε角的变化是匀速的，根据式(7)和图4、图5发现,测量系统中连杆颈测头测量的角速度是变化的，即连杆颈测头采集的轮廓数据是非等间隔的采样样本。方建超等[26]提出将原信号的幅度乘以两信号之间的间隔时间，再进行傅里叶变换的方法，实际上采集的样本会随时间变化，应该对样本先进行处理，基于等间隔样本假设和频域傅立叶变换的方法已不适用，需根据每个样本具体采样角度的实际分布进行操作，再用离散高斯加权函数进行处理。

在ISO 16610标准中，高斯低通滤波器用于工件表面纹理分析的权函数可以由下式给出：

(8)

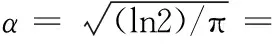
截面圆轮廓的滤波过程中，通常用截止波数Nc代替截止波长λc。本方案采用的是比较测量法，将被测轴颈与校准件进行比较， 采样数据分别是主轴颈和连杆颈直径相对校准件直径的变化量，高斯低通滤波器的权函数不依赖于轴颈的直径，所以根据式(8)可以得到用截止波数Nc表示的权函数，在等间隔采样情况下，可以将权函数进行离散化，表示为

(9)

其中，Δθ为采样的间隔角度，p表示第p个采样角。实际轴颈同步测量过程中，连杆颈的采样间隔角Δθ是非均匀变化的，与测量点的距离L和曲柄臂的长度R都有关系。与等间隔采样相比，对于非等间隔采集的样本，高斯滤波的权函数由式(7)中具体的采样角决定，按照采样角度的实际分布不同，权函数是不同的，因此可以获得每个采样角对应的权函数，表示为

(10)

p,q=1,2,…,M

其中，θp、θq表示不同的采样角度，M表示单独一个测头沿连杆颈旋转一周的采样个数。将式(10)进行归一化处理可以得到

(11)

非等间隔情况下采集的样本使用角度信息计算滤波器的系数，还要与对应的幅值信息相乘，直接在空间域中采用离散循环卷积和的方法进行高斯滤波，得到非等间隔高斯滤波后的数据为

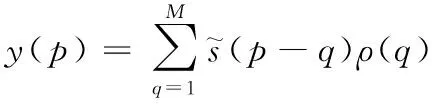
(12)

式中，ρ(q)为原始轮廓数据；y(p)为经过非等间隔权函数过滤后的数据。

3 实验验证与分析

3.1 实验系统

通过曲轴测量实验进行理论验证,同时采用文中提出的多测头消除谐波和非等间隔采样下的高斯滤波方法对采样数据和测量结果进行修正，并对曲轴零件进行形位误差的计算。

图6 曲轴测量仪实验样机Fig.6 Experimental prototype of measuring crankshaft

实验平台是与无锡富瑞德测控仪器有限公司合作开发的曲轴测量仪FRD-QZ-201890，样机如图6所示。该测量样机根据被测轴颈个数将轴颈同步测量模块安装于同一根升降座上，升降管的高度由接近开关控制，当其下降到设置高度时停止，这时测量结构中的测量臂开始下降，直到到达曲轴轴线两侧。每个测量结构下方的测量模块集成了两组测头，每组测头由两个对置的线性可变差动变压器(linear variable differential transformer，LVDT)传感器组成，并与测量臂垂直，采用激光定位仪将回转轴线精准定位，减小误差。将LVDT传感器测头用校准件进行零位标定后，对被测曲轴进行实验。

连杆颈测量结构是根据连杆颈的测量过程和测量特点设计的，且与主轴颈测量结构互不干扰，连杆颈的测量结构及测头分布情况如图7所示。测头上方的两随动轮始终与曲轴连杆颈表面接触，且使测头连线经过连杆颈中心，保证测头在旋转过程中能够采集连杆颈径向尺寸变化量。在测头下方设置两导向条使连杆颈初始状态下发生少量偏移时仍能进入测量点。

图7 连杆颈测量结构及测头分布Fig.7 Measuring structure and probe arrangement ofconnecting rod journal

3.2 实验过程

随动式测量机构的两个测头分别布置在轴线两侧，相位角相差180°，采用对置双测头对连杆颈的径向尺寸进行测量实验。随动式测量机构两个测头各自采集的数据以及均值如图8所示，可以看出，均值曲线消除了谐波，显示的为直流分量与测头初始相位偏移量的正弦和值，获取连杆颈圆轮廓更加简单快速。

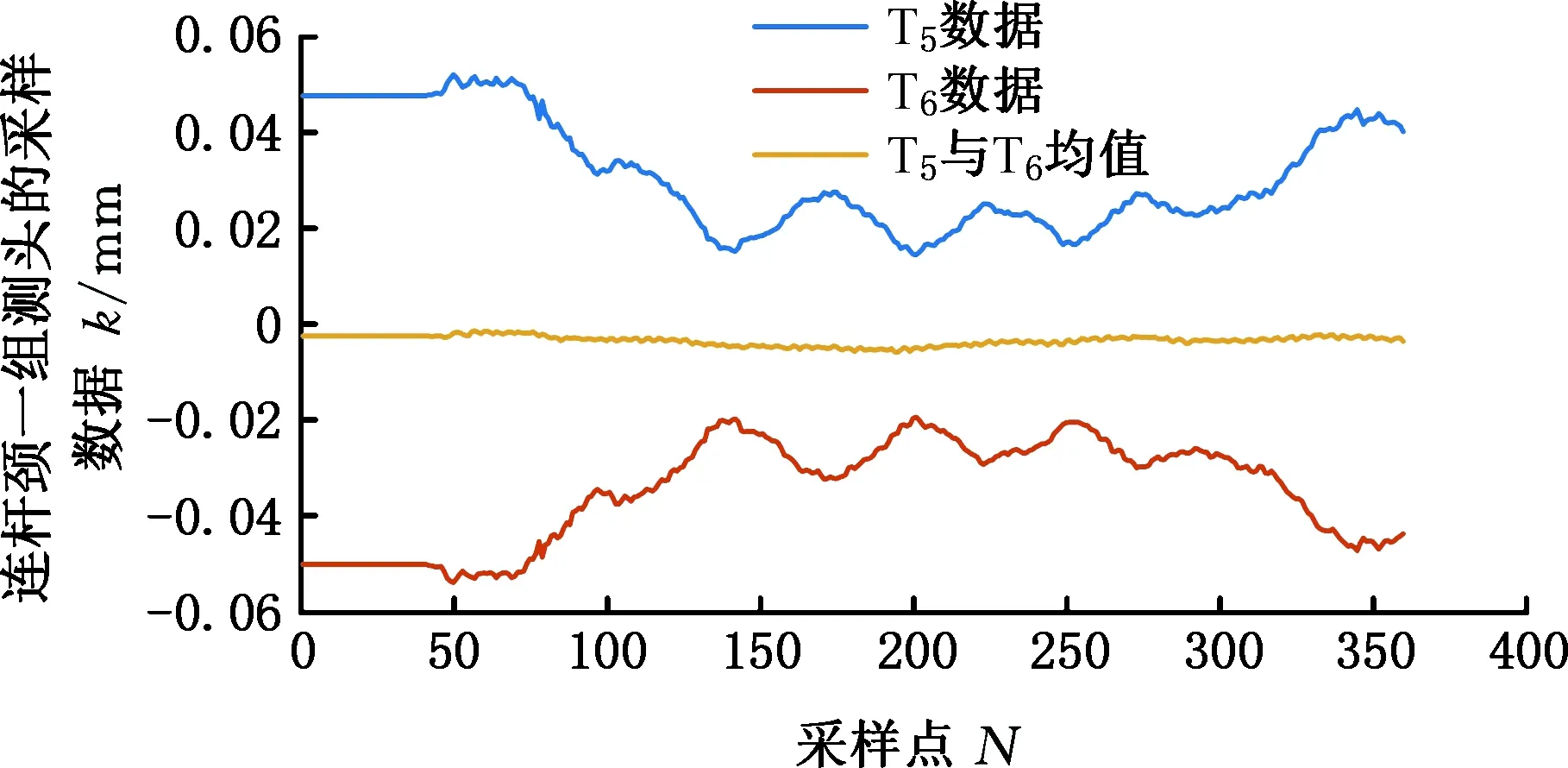
图8 连杆颈一组测头的采样数据Fig.8 Sampling data of probe on connecting rod journal

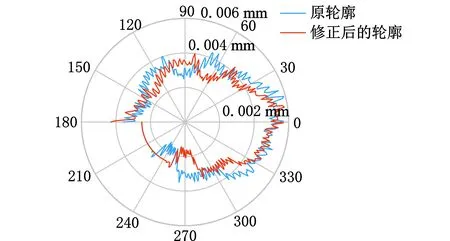
图9 极坐标下连杆颈圆轮廓Fig.9 Round profile of connecting rod journal inpolar coordinates

测头在连杆颈圆周上是非匀速移动的，所以采样数据为非等间隔排列，根据式(7)可以得到真实采样角度的排列情况，将采样数据对应真实采集角度分布，得到连杆颈的圆轮廓如图9所示，图10所示为采样点分布下的连杆颈圆轮廓。可以发现随着曲轴的回转运动，连杆颈上的采样点是先稀疏后密集，即采样间隔时间先长后短，修正之后的轮廓数据与真实的采样角度分布情况相符。

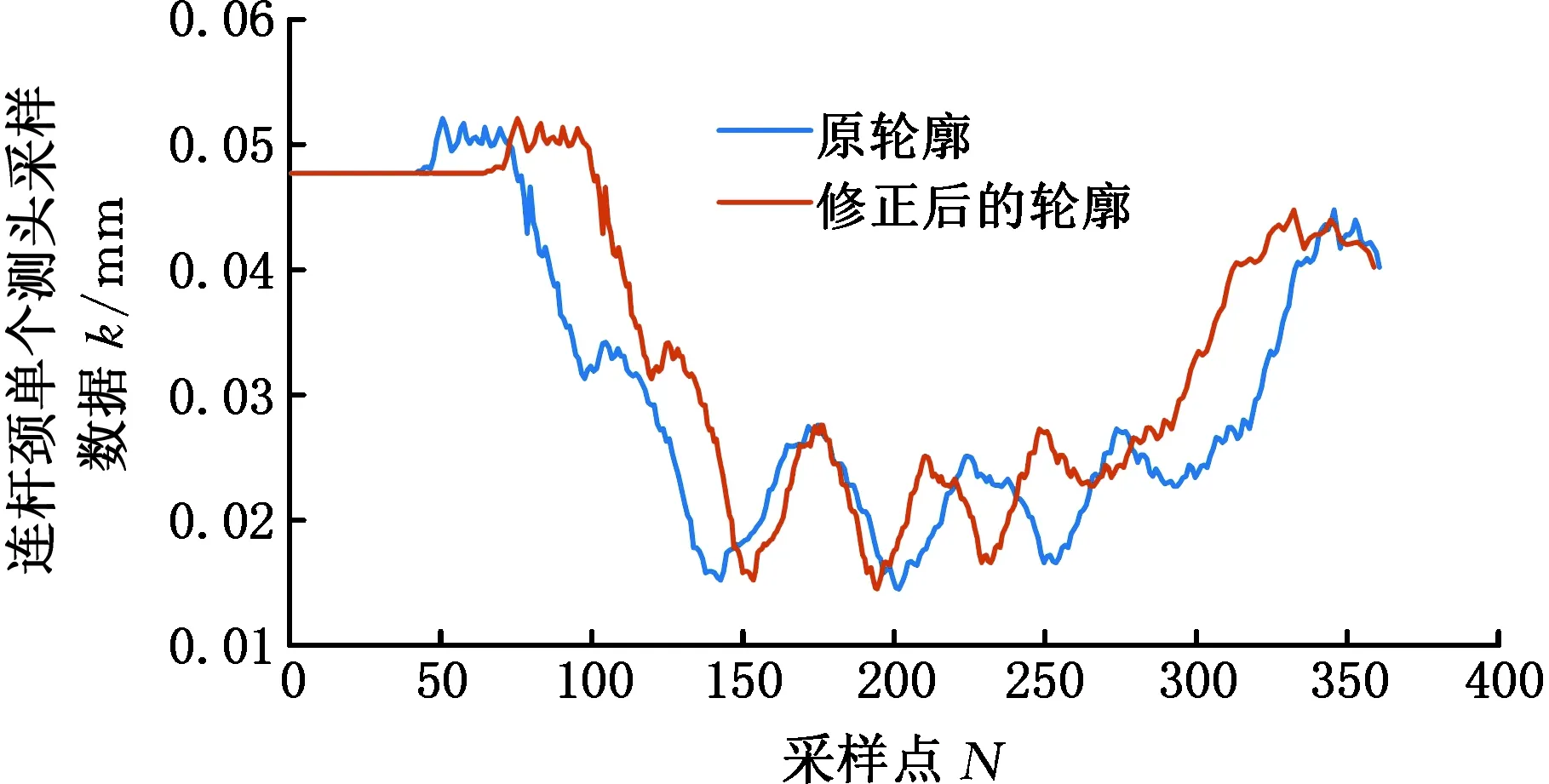
图10 连杆颈径向采样数据Fig.10 Radial sampling data of connecting rod journal

根据采样角的真实分布以及传感器测得的连杆颈圆周数据，采用本文中提到的不同采样间隔角对应不同高斯权函数的方法分别对曲轴上的四段连杆颈P1～P4进行滤波，截止波数选择50，可以得到四段连杆颈滤波后的轮廓，分别如图11所示。

由图11可以看出,滤波后的连杆颈形状轮廓一致，在某个方向上的测量误差明显，这是由测量系统误差造成的，可以利用首尾轴线修正圆心[25]，再利用最小二乘法拟合圆心和半径，得到连杆颈的直径和圆度，如表1所示。

实验室的曲轴测量仪测得各轴颈的直径平均值与三坐标测量仪测得各轴颈直径值的误差值均小于0.015 mm，测量精确度较高。对同一批次5个曲轴的每个轴颈进行多人多次测量，得到各轴颈的重复性和再现性均小于10%，测量重复性和可再现性较高，实验结果可作为比对对象。

利用曲轴测量仪对同一根曲轴的所有轴颈进行10次重复性实验，可以同时得到5段主轴颈和4段连杆颈的整个圆周测量数据。对连杆颈的测量数据进行非等间隔修正，以三坐标测量仪的测量数据为基准，将修正后的连杆颈直径值与修正前原连杆颈测量结果进行对比，数值如表2所示。连杆颈P1的直径测量误差由0.0046 mm减小到0.0023 mm，相对误差由0.0115%减小到0.0058%，连杆颈P2的直径测量误差由0.0131 mm

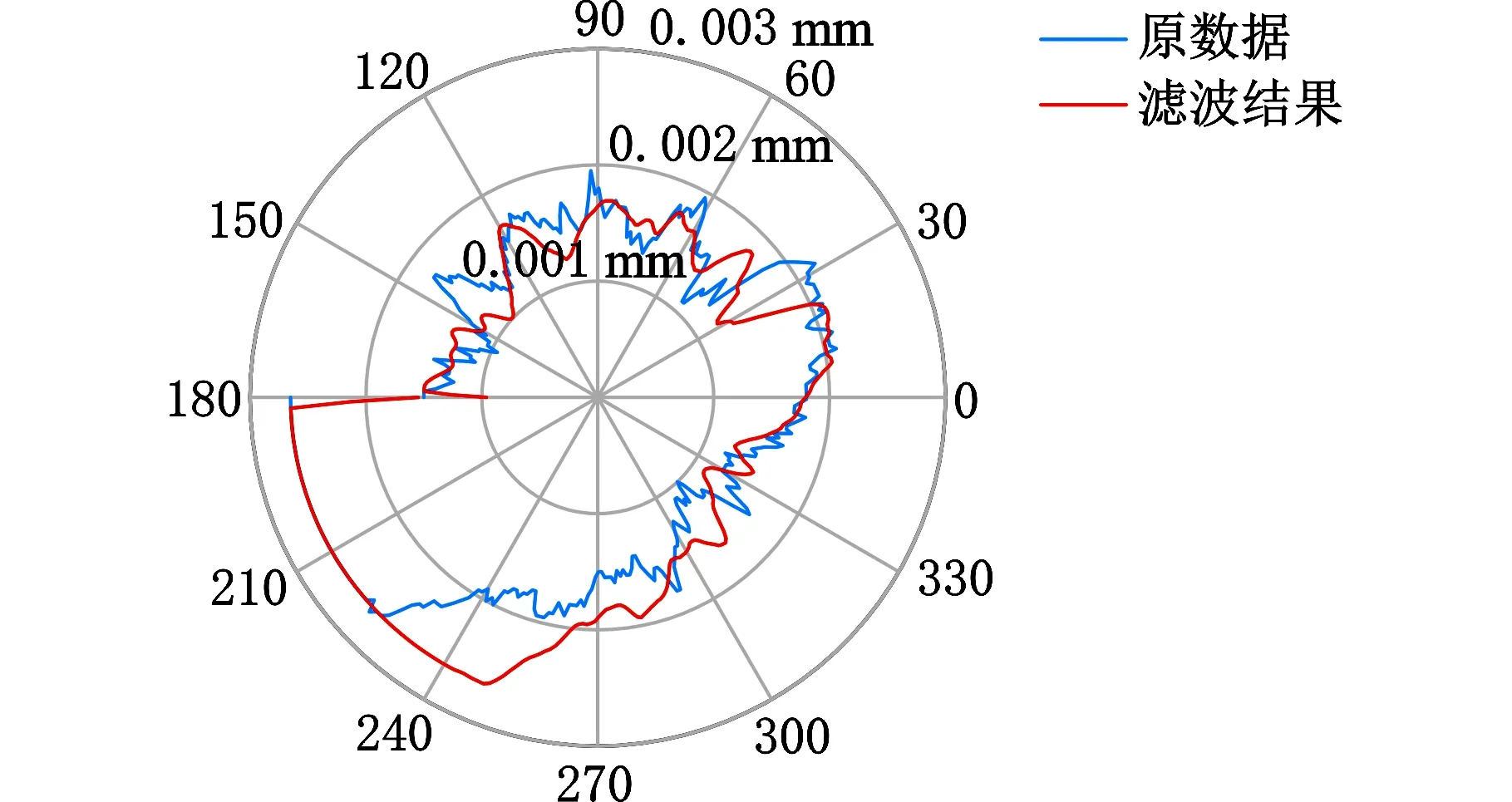
(a)连杆颈P1滤波后轮廓

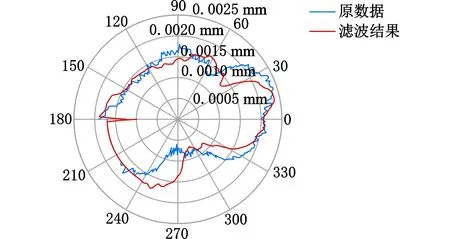
(b)连杆颈P2滤波后轮廓

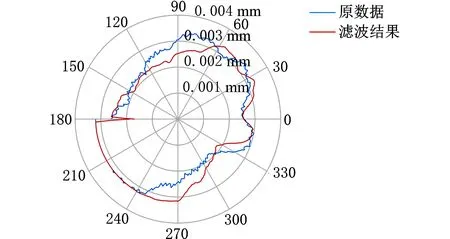
(c)连杆颈P3滤波后轮廓

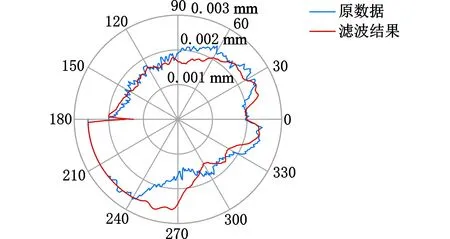
(d)连杆颈P4滤波后轮廓图11 非等间隔滤波轮廓Fig.11 Filter profile of non-equal

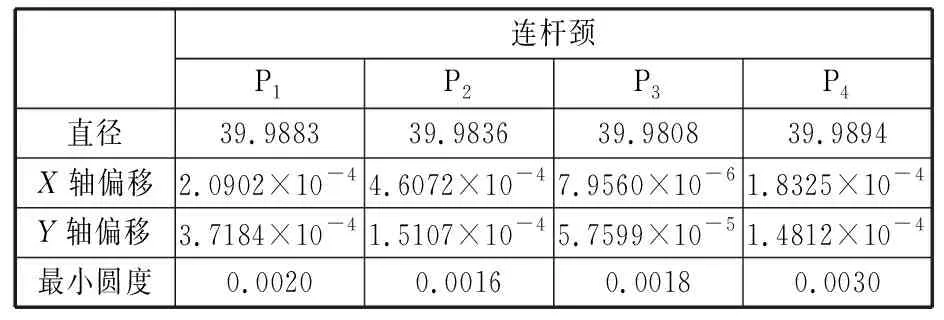
表1 连杆颈的修正结果

减小到0.0034 mm，相对误差由0.0328%减小到0.0085%，连杆颈P3的直径测量误差由0.0102 mm减小到0.0052 mm，连杆颈P4的直径测量误差由0.0083 mm减小到0.0031 mm，修正之后的误差值均小于0.0055 mm，测量误差明显减小，精确度显著提高。

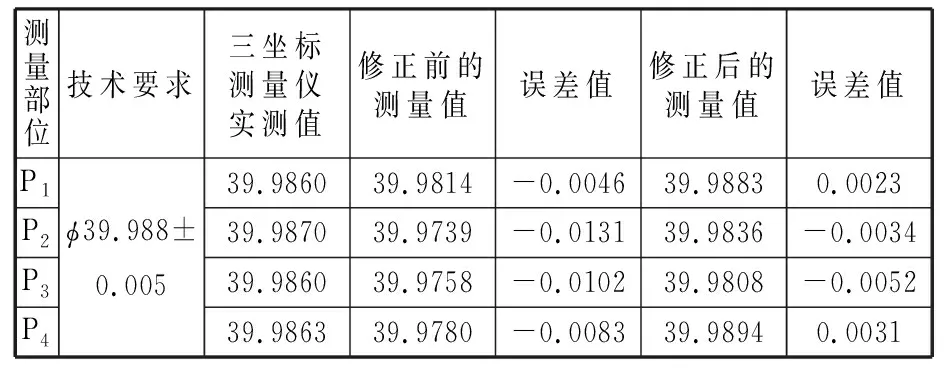
表2 连杆颈测量结果对比

4 结论

本文在接触式曲轴轴颈同步测量方法的基础上对连杆颈圆轮廓的测量展开研究。首先，将多传感器的测量数据相加消除某些谐波，使得谐波误差与测量误差得以分离。然后，根据采样角度实际分布情况计算每个采样角对应的权函数，将每个采样角对应的权函数与该角度对应的采集数据进行时域离散循环卷积计算，该处理方法通过回转轴线的运动角速度以及测头的采样间隔时间获得的采样角分布来逐点求取滤波权函数，解决了非等间隔样本数据处理问题。最后利用本文提出的多传感器消除谐波和轮廓修正方法对连杆颈测量数据进行处理，以三坐标测量仪对曲轴轴颈的测量数据为基准，将修正前后的数据进行对比，结果表明修正后4段连杆颈直径的测量误差明显减小，精确度得到明显提高，由此证明了本方案的可行性。