CP型单螺杆齿槽单次包络成形加工的研究

陈 就 夏林海 沙 丰 吴长波 陈剑平

中国民用航空局第二研究所航材技术研究中心，成都，610041

0 引言

CP型单螺杆压缩机具有体积小、容量大、单级压缩比大和效率高等其他类型压缩机无可比拟的优点，能够较好地满足军事、医药等领域对压缩机高性能和环保的要求[1]。国内外关于单螺杆压缩机的研究主要集中在压缩机几何结构优化、压缩性能、流场分析等结构和特性方面[2-5]。单螺杆压缩机中的核心零件单螺杆齿槽结构为球面包络，相比其他类型的齿类零件，其齿槽结构更加复杂，加工难度也更大。目前国内常见的CP型单螺杆(以下简称“单螺杆”)的加工方法主要有仿形车削法和圆柱二次包络铣削法[1]。仿形车削主要通过成形车刀模拟星轮齿形进行螺旋切削，车刀刃越靠近前端其切削周期越长，局部磨损也越严重，另外，车刀刀台转速慢，单次切削空行程也很大，导致仿形车削存在加工精度差和效率低等问题。圆柱二次包络铣削法结合了先进的伺服控制技术，采用成形铣刀对左右齿面分别铣削，该方法相比仿形车削法具有加工效率高、刀具磨损均匀等优点，但仍存在左右齿面分别铣削时出现接刀痕和螺杆齿槽的分度误差等缺陷。

单次包络成形加工方法是具有螺旋齿面特征零件高精度和高效率的齿形加工方法之一，采用回转刀具(如铣刀、砂轮等)加工，既可以实现成形铣削，也可以实现成形磨削，如滚刀、蜗杆、齿轮、螺杆等零件的单次包络成形，对此国内学者有深入的研究[6-10]，研究结果表明这些零件都能通过单次包络加工而成。而对于单螺杆齿槽可否采用单次包络成形加工，还有待研究。

本文根据单螺杆的螺旋齿面结构，结合空间啮合原理，建立了单次包络成形加工数学模型，分析了理论加工的误差，并根据计算得出的误差值，探究了单次包络成形应用于单螺杆加工的可行性。

1 计算坐标系及刀具的成形运动

为了便于计算，建立固定坐标系σ(OXYZ)、工件(单螺杆)坐标系σ1(O1X1Y1Z1)及刀具坐标系σ2(O2X2Y2Z2)，如图1所示。在起始状态，刀具坐标系σ2(O2X2Y2Z2)与固定坐标系σ(OXYZ)重合，工件坐标系σ1(O1X1Y1Z1)沿固定坐标系σ(OXYZ)偏置位移(0，A，0)T。

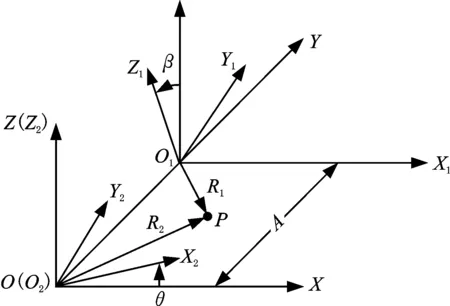
图1 计算坐标系Fig.1 Calculation coordinates system

刀具在单螺杆齿槽的成形运动有两个：单螺杆绕X1轴的转动，角速度为ω1；刀具随刀台绕Z2轴的转动，角速度为ω2。为便于描述，以右旋齿形为例进行说明，令ω1=(1，0，0)T，根据单螺杆与星轮的联动关系，有ω2=(0，0，k/z)T，其中，k为单螺杆的头数，z为与单螺杆相配星轮的齿数。成形刀具绕自身轴线Y2做回转运动与齿槽成形无关，令成形刀具的自转角速度为0。

2 成形刀具截面刃形计算

令成形刀具回转轴线Y2与固定坐标系轴线Y重合，且单螺杆在X1O1Y1轴截面上的某个齿形关于Y2轴对称的时刻称为初始状态，该截面齿形为基准齿形，如图2所示，其中B为单螺杆齿槽宽，D为单螺杆外径，h为齿槽深。对基准齿形作离散处理，所有离散点将分别在成形加工的某一时刻进入啮合，通过空间啮合原理确定刀具与螺杆接触时的空间啮合点。由啮合原理可知，这些空间啮合点既是单螺杆齿槽回转面上的点，也是成形刀具回转面上的点，将这些点分别绕Y2轴回转一定角度返回到X2OY2轴截面上，即可得到成形刀具的截面刃形。

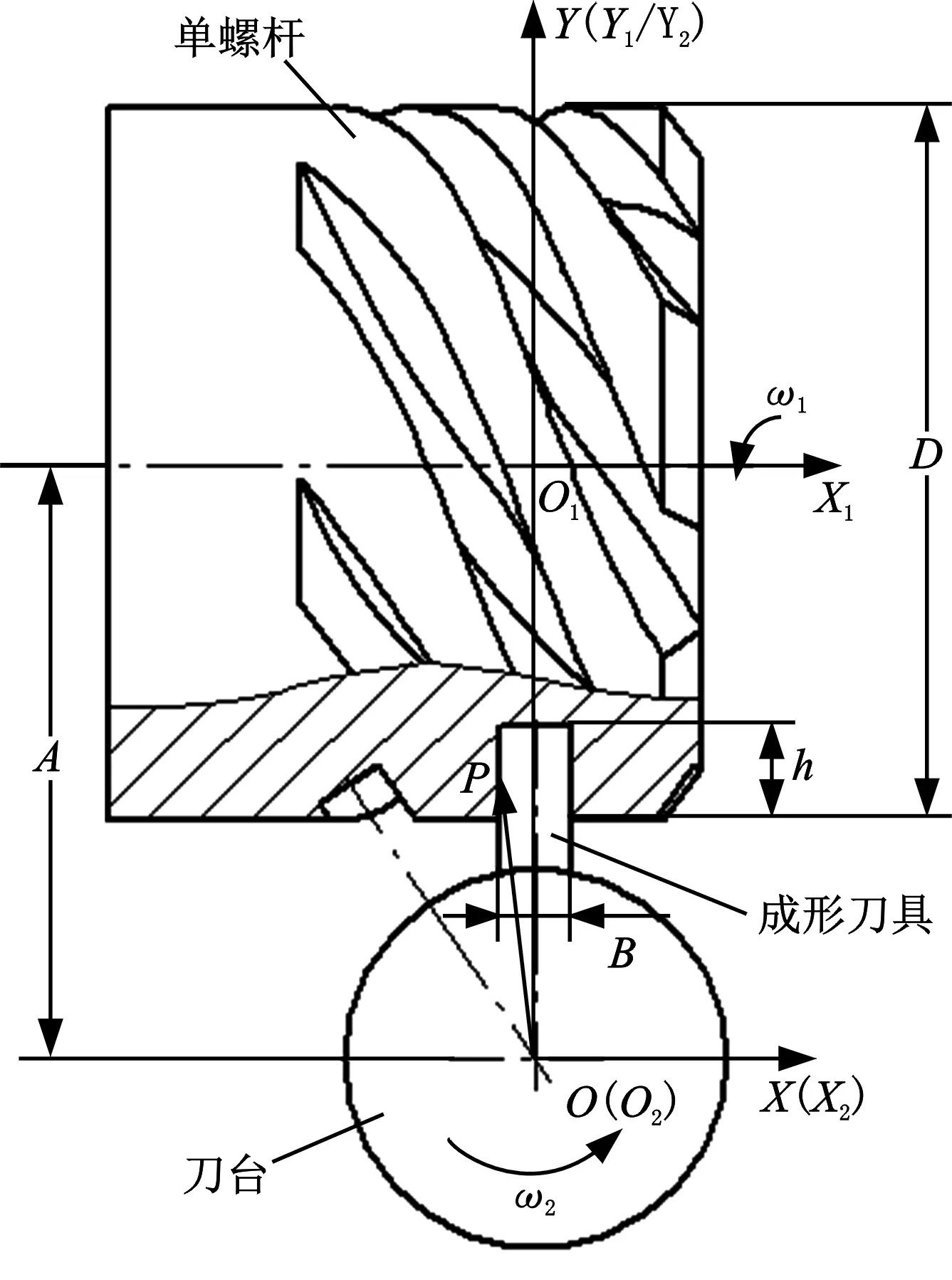
图2 加工初始状态示意图Fig2 The initial state diagram of machining

2.1 基准齿形径矢与截面切矢

将基准齿形离散成N个离散点，记任一离散点P在工件坐标系σ1中的径矢为RW，截面切矢为τW，由于P点及其截面切矢τW均在轴截面X1O1Y1上，因此对基准齿形方程上的P点求导，有

(1)

式中，f(x，y)为X1O1Y1轴截面上的基准齿形方程。

设P点进入啮合时，螺杆转动角度为β，刀台转动角度为θ，由前述联动关系可知：

(2)

通过坐标变换可知，在固定坐标系中的径矢和切矢分别为

(3)

(4)

j=(0，1，0)T

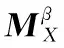
在刀具坐标系中的径矢和切矢分别为

(5)

(6)

2.2 P点的相对运动速度

在固定坐标系σ(OXYZ)中，P点处的成形运动有两个，分别为随螺杆绕X1轴转动的线速度v1和随刀台绕Z2轴转动的线速度v2：

v1=ω1×(R-Aj)

(7)

v2=ωT×R

(8)

在坐标系σ(OXYZ)中，当P点成为啮合点时，该点处的相对运动速度为

v12=v1-v2

(9)

2.3 回转刀具在P点处的法矢

单螺杆齿槽面由成形刀具单次包络而成，且齿槽基准齿形是包络面上的曲线，由解析几何可知，在固定坐标系σ中，P点处的法矢n垂直于P点的相对运动速度v12和截面切矢τ：

n=v12×τ

(10)

转至刀具坐标系σ2(O2X2Y2Z2)中即为

(11)

2.4 空间啮合线

P点为啮合点时，由啮合原理可知[11]，在刀具坐标系σ2中，回转刀具上的径矢RT、法矢nT及回转刀具的回转轴线方向向量j三者的混合积为0，即

(RT，nT，j)=0

(12)

解式(12)可以得到P点成为啮合点时螺杆的转动角度β，代入式(3)中可以得到P点在固定坐标系σ中的啮合点径矢。

由于P点是基准齿形中离散点中的任意一点，故对所有离散点按以上方法进行计算就可以得到基准齿形中每一个离散点在进入啮合时螺杆的转动角度βi(i=1～N，N为计算的离散点个数)。将每一个βi代入径矢R计算式中，可以得到一系列离散点在固定坐标系σ中的啮合点径矢矩阵，进而得到单螺杆基准齿形在单次包络成形时的空间啮合线。

2.5 回转刀具截面刃形

将上述每一个计算得到的βi值依次代入式(5)中，就可以得到空间啮合线在刀具坐标系σ2中的径矢矩阵。由于空间啮合线也在回转刀具回转面上，故依次将空间啮合线上所有离散点绕Y2回转至回转刀具轴截面(X2OY2)上，设第i点的回转角度为αi，将该点回转到刀具轴截面(XTOYT)上的径矢为

(13)

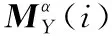
同理可以得到该点的截面法矢：

(14)

回转后RS(i)是截面(XTOYT)上的点，其Z向分量为0，令

Z(RS(i))=0

(15)

求解式(15)可得出第i点的回转角度αi，代入RS(i)和nS(i)计算式中，即可求得第i点的截面径矢和截面法矢，也即对应基准刃形上的任意点P都可以在回转刀具截面刃形上得到一点F与之对应。对所有离散点进行求解即可得到成形刀具截面刃形上所有离散点的截面径矢和截面法矢，对径矢点进行曲线拟合，即可得到回转刀具的截面刃形。

3 成形误差计算

成形误差指单螺杆在过X1轴的任意轴截面上齿形离散点的理论径矢和单次包络成形径矢之间的齿形偏差。根据单螺杆齿槽面的成形原理，理论径矢可以通过基准齿形上的离散点沿特定的螺旋线扫掠得到。齿槽截面成形包络径矢方程则需要根据上述计算得到的成形刀具截面径矢和法矢，结合理论径矢所在的齿形轴截面，运用啮合原理反推得到。

3.1 理论齿槽曲面径矢方程

进行误差计算时，设过螺杆轴线的任一齿槽轴截面与基准齿形所在轴截面之间的夹角为γ，记该齿槽轴截面为γ轴截面。γ轴截面齿形上Q点由基准齿形上任意点P扫掠得到，将该点回转至螺杆所在的齿槽截面上，可得到螺杆在工件坐标系σ1中的螺旋面径矢方程：

(16)

由于P点为基准齿形上的任意一点，因此将基准齿形上的所有离散点代入式(16)中，就可以得到单螺杆γ轴截面上齿形的所有离散点的理论径矢方程。

3.2 包络成形齿槽曲面径矢方程

在包络成形中，单螺杆γ轴截面上的齿形离散点由前述计算得到的成形刀具截面刃形离散点通过啮合计算得到。由前文可知，成形刀具截面刃形离散点由基准刃形离散点通过啮合计算得到，也即基准刃形的离散点之间存在一一映射关系。也就是说基准刃形上的离散点P通过其对应的空间啮合点回转到刀具截面刃形上，对应刀具截面刃形上的F点，同理，通过啮合计算，也可以得到与F点相对应的单螺杆γ轴截面上的E点，如图3所示。

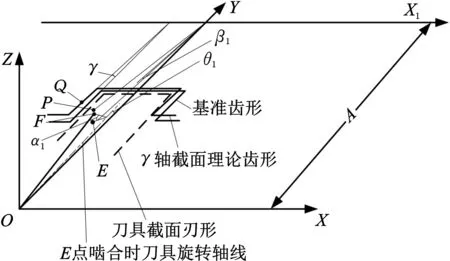
图3 E点啮合计算说明图Fig.3 E point meshing calculation diagram

当E点进入啮合时，E点与F点重合，记此时单螺杆转角为β1，对应刀台转角为θ1，F点绕Y2轴旋转至E点位置，转动角度为α1，根据联动关系有

(17)

此时，E点在刀具坐标系中的径矢和法矢分别为

(18)

(19)

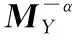
在固定坐标系中的径矢和法矢分别为

(20)

(21)

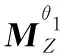
随螺杆及刀台的转动速度分别为

v3=ω1×(RE-Aj)

(22)

v4=ω2×RE

(23)

啮合时其相对运动速度为

v34=v3-v4

(24)

依据啮合原理，有

nv34=0

(25)

E点在工件坐标系中的径矢为

(26)

又由于E点在γ轴截面齿形上，根据几何关系有

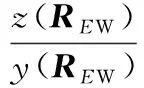
(27)

联合式(25)、式(27)可求出E点成为啮合点时相应的转角α1和φ1，代入RE表达式中即可得到对应γ轴截面上E点的径矢。将成形刀具截面上所有点代入运算，即可得到单螺杆上对应γ轴截面齿形的包络线。同理对每一个螺杆转角γ进行求解即可得到螺杆齿形的包络成形曲面。

3.3 误差计算

由前述计算分别得到了单螺杆基准齿形上的P点对应γ轴截面齿形上的理论点Q和包络成形点E的径矢。Q点和E点的距离就是对应P点在γ轴截面上的成形误差：

(28)

通过对基准刃形上所有离散点进行计算就可以得到任意夹角γ下的齿形成形误差分布。

4 实例计算

应用上述单次包络成形计算方法，对一种常见规格的单螺杆齿槽分别计算其包络成形加工刀具的截面刃形和单螺杆单次包络成形误差。在计算中，本文只对包络成形加工的可行性作定性分析，为简化计算过程，不考虑成形包络点落在单螺杆几何体以外的情况。

4.1 实例参数

某型单螺杆部分设计参数如下：螺杆外径D=300 mm，齿深h=40 mm，齿宽B=30 mm，齿根圆弧半径r=3 mm，头数k=6；螺杆星轮中心距A=250 mm，相配星轮齿数z=11。

4.2 成形刀具截面刃形计算及优化

取基准齿形离散点个数N=49，利用MATLAB软件对齿形进行离散计算，离散后所有离散点的基准齿形见图4。

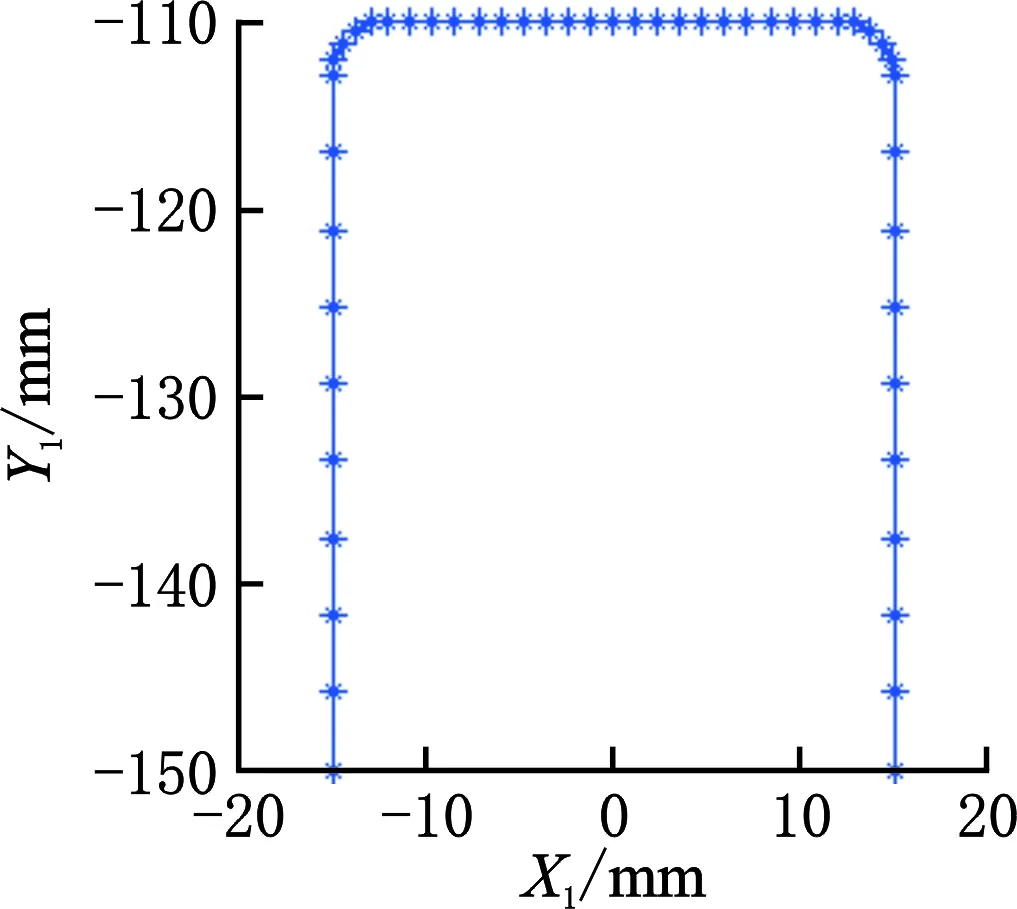
图4 离散点的基准齿形Fig.4 Base tooth profile of discrete dots

基准齿形所有离散点进入啮合时，在固定坐标系σ中的空间啮合位置如图5所示。

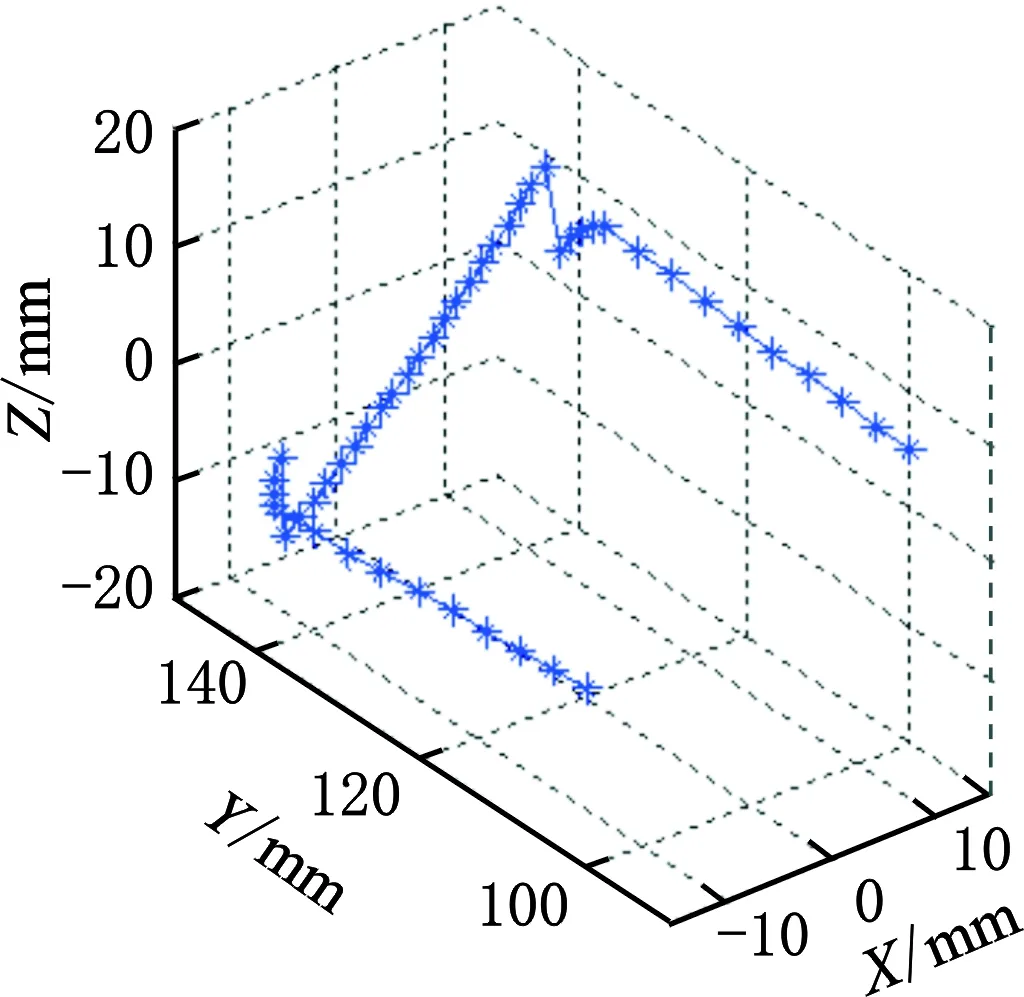
图5 离散点的空间啮合位置Fig.5 Space meshing position of discrete dots

由图5可以看出，齿根线两端点在啮合时，啮合点位置产生了突变，对应到基准齿形上为圆弧段与齿根线的交点位置。此时，需检查求解式(12)，判断变量β1在其有效的成形转角范围内是否为唯一解。由包络成形加工方法可知，成形刀具的直径应不大于所在齿槽位置的宽度，否则在实际应用中会产生干涉。根据解析几何，以左齿面的交点为例进行说明，所有离散点的转角β1的解空间应满足：

(29)

根据式(12)，令

f(β1)=(RT，nT，j)

(30)

可得函数f(β1)和变量β1之间的关系曲线，如图6所示。f(β1)在解空间内单调递增，仅有一个解，说明齿根线两端点在啮合时，不存在除计算出的啮合点位置之外的其他可能的空间啮合点位置，也即基准齿形在包络成形时，该点处确实存在啮合位置突变。

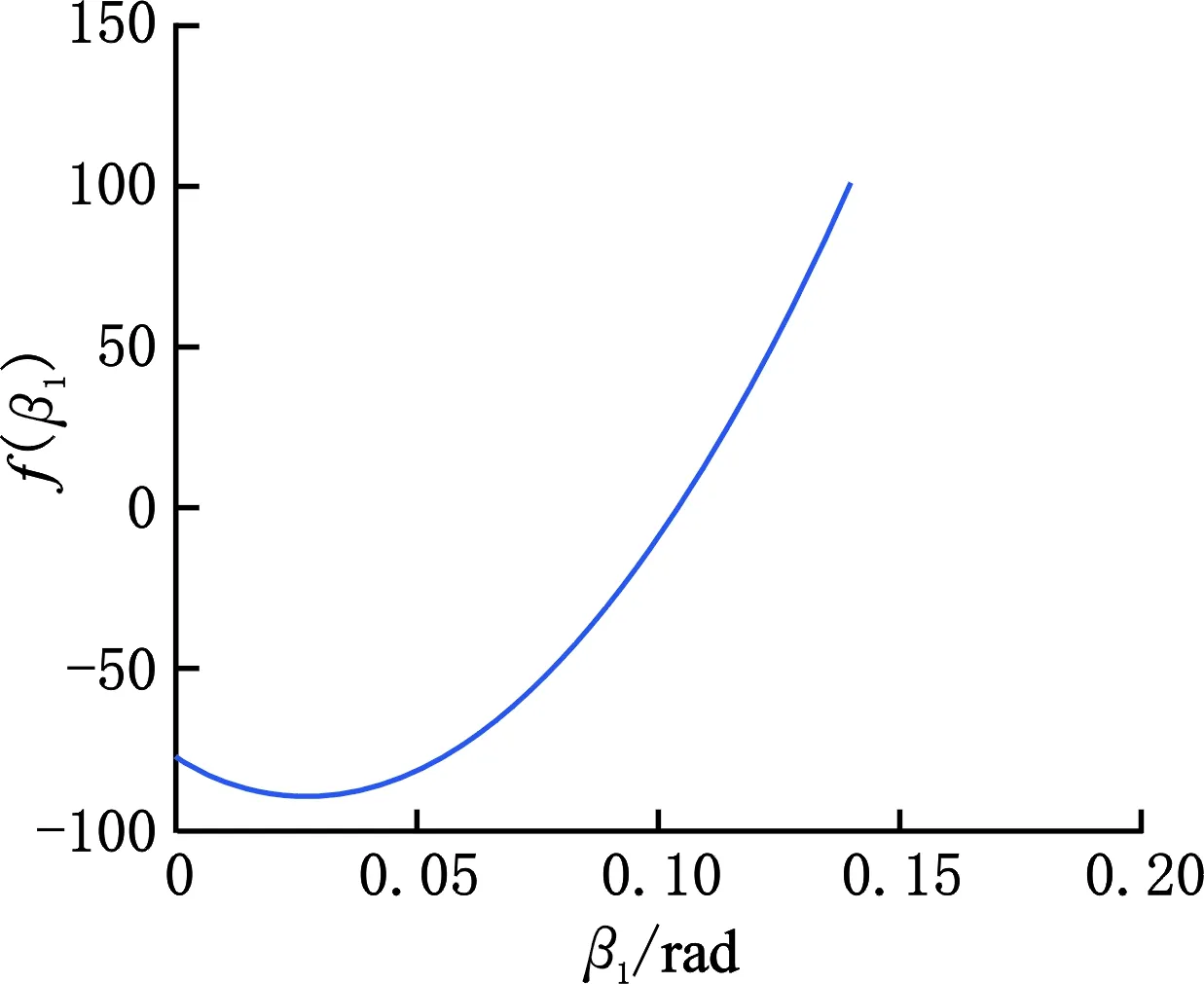
图6 函数f(β1)在解空间内的曲线图Fig.6 Curve graph of function f(β1)in solution space

根据离散点的空间啮合位置，进一步求得基准齿形对应的包络成形的成形刀具截面刃形，如图7所示。由图7可以看出，由于齿根线两端点的空间啮合点位置发生了突变，导致成形刀具截面刃形在对应点处产生了突出的尖角，该刃形是无法应用于实际的。如果要应用单次包络成形进行单螺杆齿槽的成形加工，则需要优化设计参数。不断增大齿根圆弧半径r值，然后分别进行计算，结果表明，增大齿根圆弧半径能有效缓解刃形的尖角突出的问题，此处给出了具有代表性的r=7，10，15 mm(此时基准齿形无直线齿根线)对应的成形刀具截面刃形，分别如图8～图10所示。

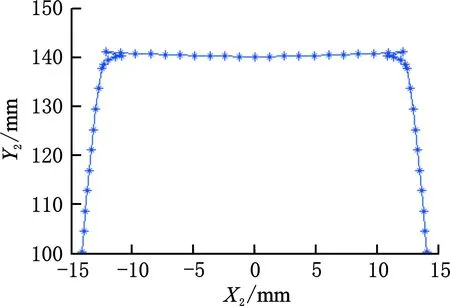
图7 成形刀具截面刃形(基准齿形)Fig.7 Curve graph of forming tool profile(base tooth profile)

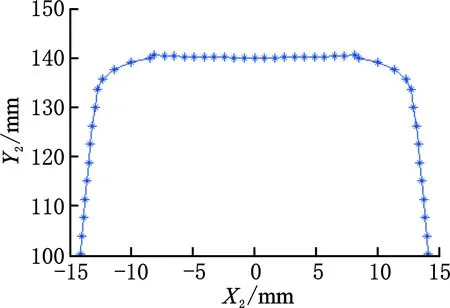
图8 成形刀具截面刃形(r=7 mm)Fig.8 Curve graph of forming tool profile(r=7 mm)

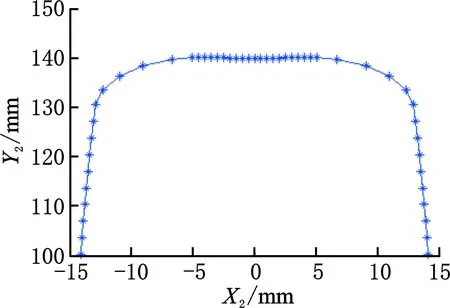
图9 成形刀具截面刃形(r=10 mm)Fig.9 Curve graph of forming tool profile(r=10 mm)

由图8和图9可以看出，如果基准齿形上的齿根线为直线，那么该齿根线对应的成形刀具截面刃形内凹，在该段刃形的两端就会产生曲率突变，在实际应用中，该两点位置就会产生急剧磨损，影响加工精度，不是包络成形理想的基准齿形。而由图10可以看出，将齿根线直接改成了圆弧后，离散点的啮合空间位置(图11)和成形刀具截面刃形均平滑过渡，是包络成形理想的基准齿形。为此，下面将对r=15 mm(齿根为圆弧)的截面齿形进行包络成形误差分析。

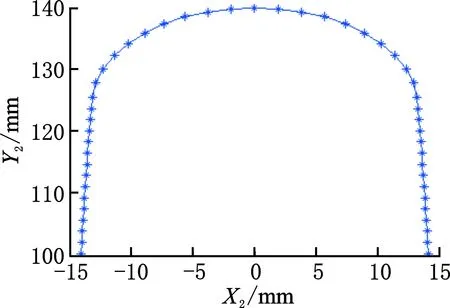
图10 成形刀具截面刃形(r=15 mm)Fig.10 Curve graph of forming tool profile(r=15 mm)

图11 离散点的空间啮合位置(r=15 mm)Fig.11 Space meshing position of discrete dots(r=15 mm)

4.3 基准齿形优化后的误差计算

在成形误差分析中，基于单螺杆齿槽关于Y1轴的对称性，计算Y1轴齿槽长的一侧(图2中Y1轴的左侧)的误差即可。根据联动和几何关系可得到该侧齿槽转角γ的取值范围：

(31)

将设计参数代入计算可得：0≤γ≤96.47°。从0°开始每隔5°取一个误差计算截面，最后一个截面取γ=96.47°，得到的理论和单次包络成形曲面对比图见图12，局部放大图见图13。

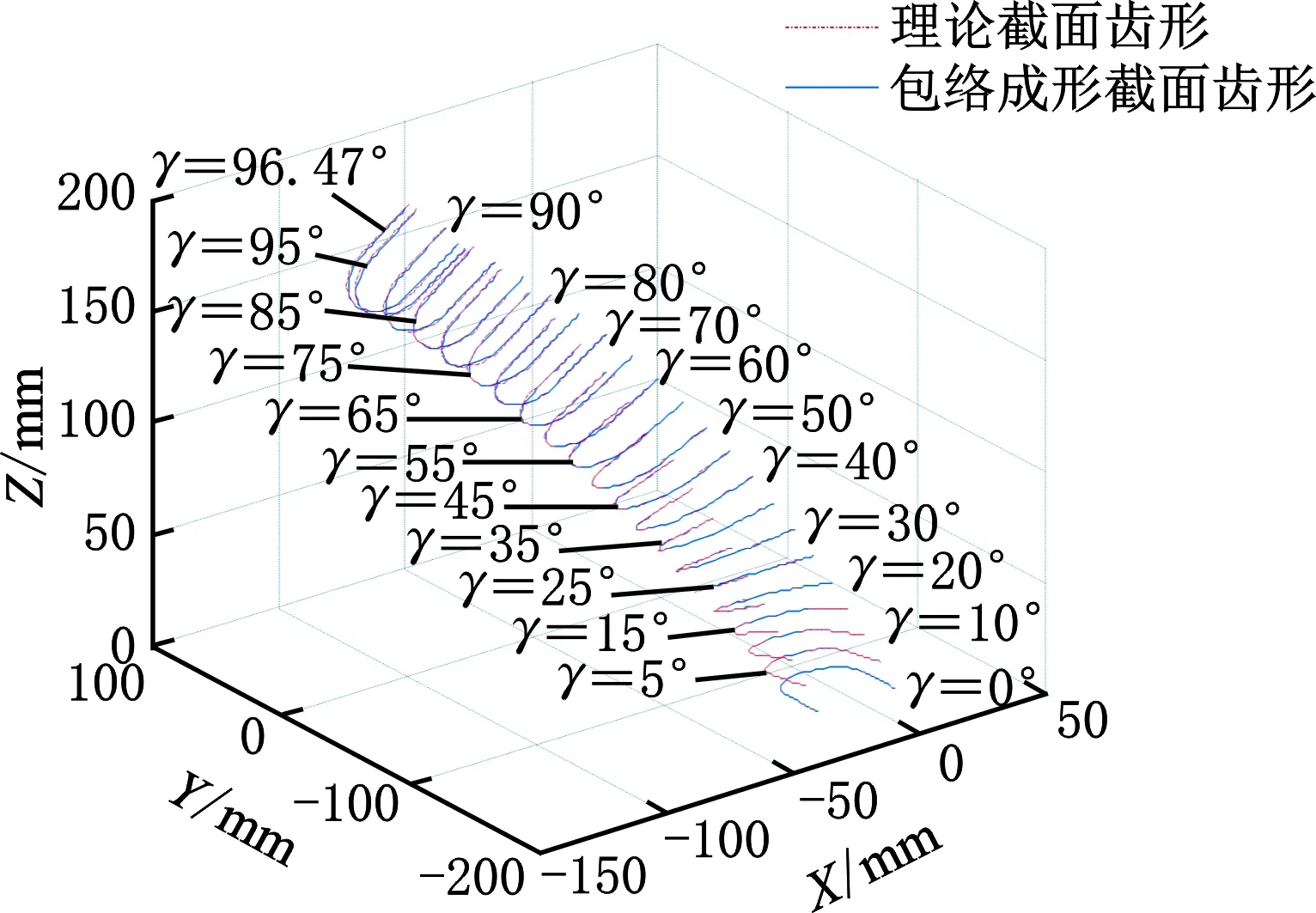
图12 理论和包络成形曲面对比图Fig.12 Curve graph of comparison between theory and envelope forming surface

图13 理论和包络成形齿形对比局部放大图Fig.13 Partial enlarged detail curve graph of comparison between theory and envelope forming surface

对每一个γ轴截面上理论和包络成形齿形之间的误差值进行计算，计算结果和齿形误差分布如图14所示，最大误差为1.061 mm。

图14 不同γ轴截面上齿形误差分布情况Fig.14 The tooth profile error distribution on different axis sections with correspond γ angles

4.4 计算结果分析

从以上计算结果可以看出：

(1)当单螺杆基准齿形的齿根线为直线时，其包络成形刀具的截面刃形在对应齿根线左右两端点位置会出现突出尖角，该两点处左右两侧的曲率变化量和齿根圆角半径值有直接关系，当齿根圆角增大时，曲率变化量会减小，刃形曲线会更加平滑，但突出的尖角始终存在。

(2)当单螺杆基准齿形的齿根线为圆弧时，其包络成形刀具的截面刃形平滑，无尖角突出，但单次包络成形导致的齿形误差值较大，最大位置的误差超过了1 mm。

(3)优化后的基准齿形成形误差分布特点为：齿形误差值在齿形的中心点处为零，向两侧先增大后减小，且两侧的误差值不对称，对于右旋螺杆，其左齿面误差值较大；随着转动角度γ的不断增大，γ轴截面上的齿形点进入啮合时，刀台的转动角度也不断增大，相对于基准齿形上的点，其相对速度的变化量也逐渐变大，导致误差也逐渐增大。

5 结论

(1)对CP单螺杆齿槽的单次包络成形方法进行了理论研究，依据啮合原理建立了采用单次包络成形加工刀具截面刃形、理论齿槽曲面径矢及包络成形齿槽曲面径矢的计算方法与公式。

(2)利用该计算方法对一种常规的单螺杆齿槽进行了计算，结果表明该方法加工单螺杆齿槽曲面成形误差较大，且离齿槽中心点越远误差值越大，无法通过单次包络成形加工方法将CP型单螺杆齿槽一次加工成形。