基于分层贝叶斯模型的齿轮弯曲疲劳试验分析

毛天雨 刘怀举 王宝宾 侯圣文 陈地发

1.重庆大学机械传动国家重点实验室，重庆，4000442.陕西法士特齿轮有限责任公司，西安，710077

0 引言

齿轮广泛应用于航空、航天、舰船、高铁、海洋装备等领域，其服役性能直接决定了整机装备的可靠性[1]，而且齿轮弯曲疲劳失效导致的装备事故和人机安全问题日益突出[2]，因此开展齿轮弯曲疲劳试验非常必要。以试验基础数据为主要支撑是进行高可靠齿轮设计的必要前提，同时也是对齿轮疲劳寿命等服役性能最为直接和有效的评估手段。

齿轮弯曲疲劳试验基础数据一般指可靠度-应力-寿命(P-S-N)曲线，它也是齿轮疲劳强度设计的基本参数。获取P-S-N曲线通常采用成组法，在4～5个应力级下进行试验，每个应力级下不少于5个试验点[3]。但由于齿轮弯曲疲劳试验结果受齿轮材料微结构特征、加工工艺、表面质量等多种不确定性因素的影响，试验寿命数据分散明显，一般情况下难以获得满足传统统计方法所需要的大样本数据。目前小样本疲劳试验数据的分析方法，一类是通过改进大样本统计方法，如傅慧民等[4]在假设疲劳寿命服从对数正态分布的前提下，采用异方差回归分析的方法对疲劳试验数据进行整体分析；XIE等[5]提出了一种基于样本信息聚集原理的P-S-N曲线数据处理方法，通过将在不同应力水平下测试的疲劳寿命转换成在任意应力水平下的等效寿命，将小样本数据转换为大规模样本；GAO等[6]基于P-S-N曲线在高应力区某一点相交的假设，实现了P-S-N曲线的快速获取。另一类是通过样本扩充，使之尽可能适应大样本数据统计方法。如马宇鹏等[7]提出了Bootstrap-支持向量回归-二阶累次量的方法框架和多阶虚拟样本容量扩充的方法，解决了小样本分析的问题；赵远等[8]基于Bootstrap法充分挖掘试验数据的寿命与可靠性总体信息，提高了小子样数据评估的准确性。然而样本数据扩充方法的本质依然是进行频率统计，当样本量较小时，进行样本扩充可能会产生误差。另外，传统的概率方法往往需要大量的疲劳试验数据作为依托，而齿轮疲劳试验耗时耗力，商用谐振式高频疲劳试验机加载频率一般为50～100 Hz，依据ISO 6336标准规定的3×106次循环基数，一个试验点要进行17 h(按50 Hz计算)的试验，这导致通常可用于分析的疲劳试验数据往往是小样本的，而贝叶斯统计方法可用于推断疲劳测试数据并处理不确定性，可通过不断更新和融合数据来解决样本量较少这一问题。GUIDA等[9]借助贝叶斯理论和先验信息，将材料疲劳性能参数引入先验分布中，发现无论是点估计还是区间估计，所提出的贝叶斯方法远优于经典频率理论方法；刘建中等[10]运用模糊综合评判方法综合经验信息来确定先验分布，同时基于贝叶斯理论给出了一种由小样本试验数据确定疲劳寿命分布的可靠方法。然而，上述方法均是采用经验贝叶斯方法，其先验分布的选取易受到主观信息的影响，在缺乏先验信息的情况下往往存在争议。而分层贝叶斯可以避免超参数的选取，能够提供一种更具鲁棒性的统计分析手段[11]。

本文开展了8620H钢表面渗碳齿轮弯曲疲劳试验，并针对传统统计方法处理小样本齿轮弯曲疲劳试验数据拟合失真的问题，基于贝叶斯理论建立了齿轮弯曲疲劳P-S-N曲线的分层贝叶斯模型，给出了在无先验信息下分布参数的选取方法，通过Gibbs采样对模型进行求解并获取模型参数的后验分布。结合齿轮弯曲疲劳试验数据，以50%和99%可靠度下S-N曲线相对斜率比为拟合结果评价指标，验证了分层贝叶斯模型在小样本数据下的稳定性与优越性。

1 齿轮弯曲疲劳试验

轮齿弯曲疲劳破坏是齿轮最严重的失效形式之一，航空齿轮的断齿甚至还会导致机毁人亡的惨剧[12]，因此，将齿轮弯曲疲劳失效作为研究对象，通过试验获得齿轮的弯曲疲劳寿命数据与齿轮弯曲疲劳P-S-N曲线，对指导高性能齿轮正向设计具有显著的工程意义。

1.1 齿轮试样

齿轮试样参数如表1所示，制造工艺路线为：毛坯锻造→粗车→半精车与精车→滚齿→渗碳淬火→磨齿。所有试验齿轮均采用相同的加工设备及加工工艺，且在同一炉进行热处理。

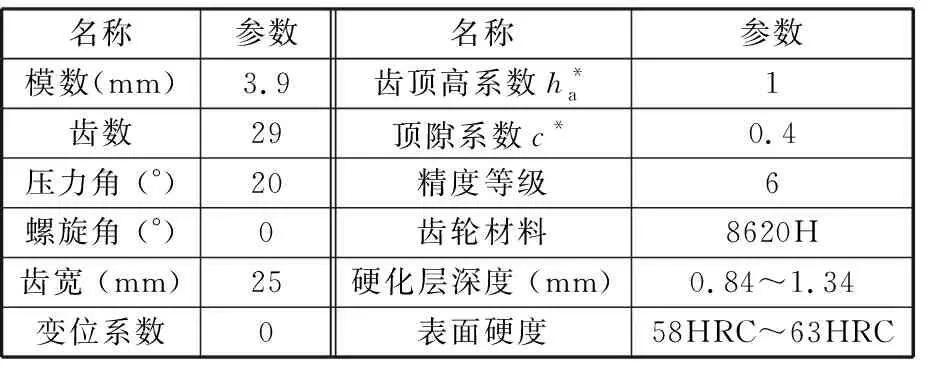
表1 试验齿轮基本参数

1.2 试验方法

齿轮弯曲疲劳试验通常采用脉动加载方式[13]，通过疲劳试验机上的夹具对试验齿轮轮齿进行脉动加载，直至轮齿发生弯曲疲劳失效或越出(循环基数通常为3×106)。试验中，脉动载荷仅施加在试验齿轮轮齿上，试验齿轮不做啮合运转。

成组法是齿轮弯曲疲劳试验中的常用方法，该方法通过在4～5个应力级下进行多组寿命测试来获得齿轮在各个应力级下的寿命分布，进而获得齿轮的弯曲疲劳P-S-N曲线。图1为P-S-N曲线示意图，分别代表了1%、50%、99%可靠度下的S-N曲线。

1.3 试验设备

试验采用Zwick 1000 kN弯曲疲劳试验机和 GB/T 14230—1993标准[14]中脉动加载的形式，对试验齿轮进行脉动循环加载，以获得某恒定载荷级下的齿轮弯曲疲劳寿命。弯曲疲劳试验机基本参数如表2所示，齿轮弯曲疲劳试验现场如图2所示。

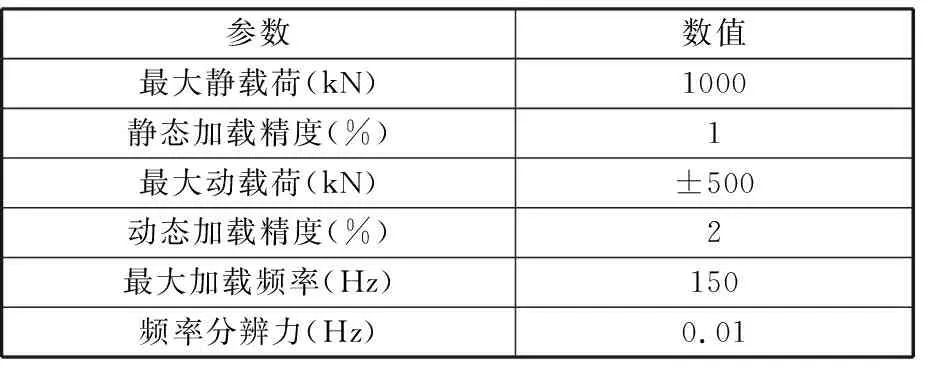
表2 弯曲疲劳试验机基本参数

图2 齿轮弯曲疲劳试验Fig.2 Gear bending fatigue test

1.4 齿轮失效的检测与判据

试验过程中，疲劳试验机通过脉动循环加载与齿轮发生共振，其共振频率和疲劳试验机与齿轮组成的总刚度和质量有关[15]。当齿轮出现裂纹后，系统刚度减小，从而引起频率的下降。根据GB/T 14230—1993标准[14]的要求，当满足以下两者之一的条件即可判定齿轮发生失效：①出现可见裂纹或断齿；②频率下降5%～10%。

1.5 试验数据的预处理

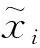
(1)

水边植物群落和建筑周边植物群落在各指标上都有一定程度的下降,根据驳岸类型和与建筑的位置关系进一步分析(图6)。

2 试验数据处理方法

齿轮弯曲疲劳试验数据常用的统计方法有正态分布、对数正态分布、双参数威布尔分布和三参数威布尔分布[19]。由于模型可及性和许多计算工具易于找到，对数正态分布在疲劳试验数据处理中被广泛使用[20-21]，因此，在本文数据处理中，采用对数正态分布拟合，通过成组法数据确定疲劳曲线的有限寿命阶段，即齿轮的P-S-N曲线方程。

2.1 基于频率理论的P-S-N曲线拟合

在有限寿命阶段，可靠度P下的失效循环次数NP与应力S满足Basquin方程[22]：

SmPNP=CP

(2)

式中，mP、CP为材料参数，mP>0，CP>0。

通过对式(2)左右两边取对数，可以得到线性表达式：

lgNP=lgCP-mPlgS

(3)

由式(3)可以看出，Basquin方程在双对数坐标下呈现出线性关系。

如图3所示，获取齿轮弯曲疲劳P-S-N曲线，首先需要确定各应力水平下的疲劳寿命分布，其次需要确定各应力水平下可靠度P下的疲劳寿命NP，进而通过最小二乘法(least squares method，LSE)对式(3)进行拟合以获取P-S-N曲线，具体计算流程可参考GB/T 14230—1993标准[14]。

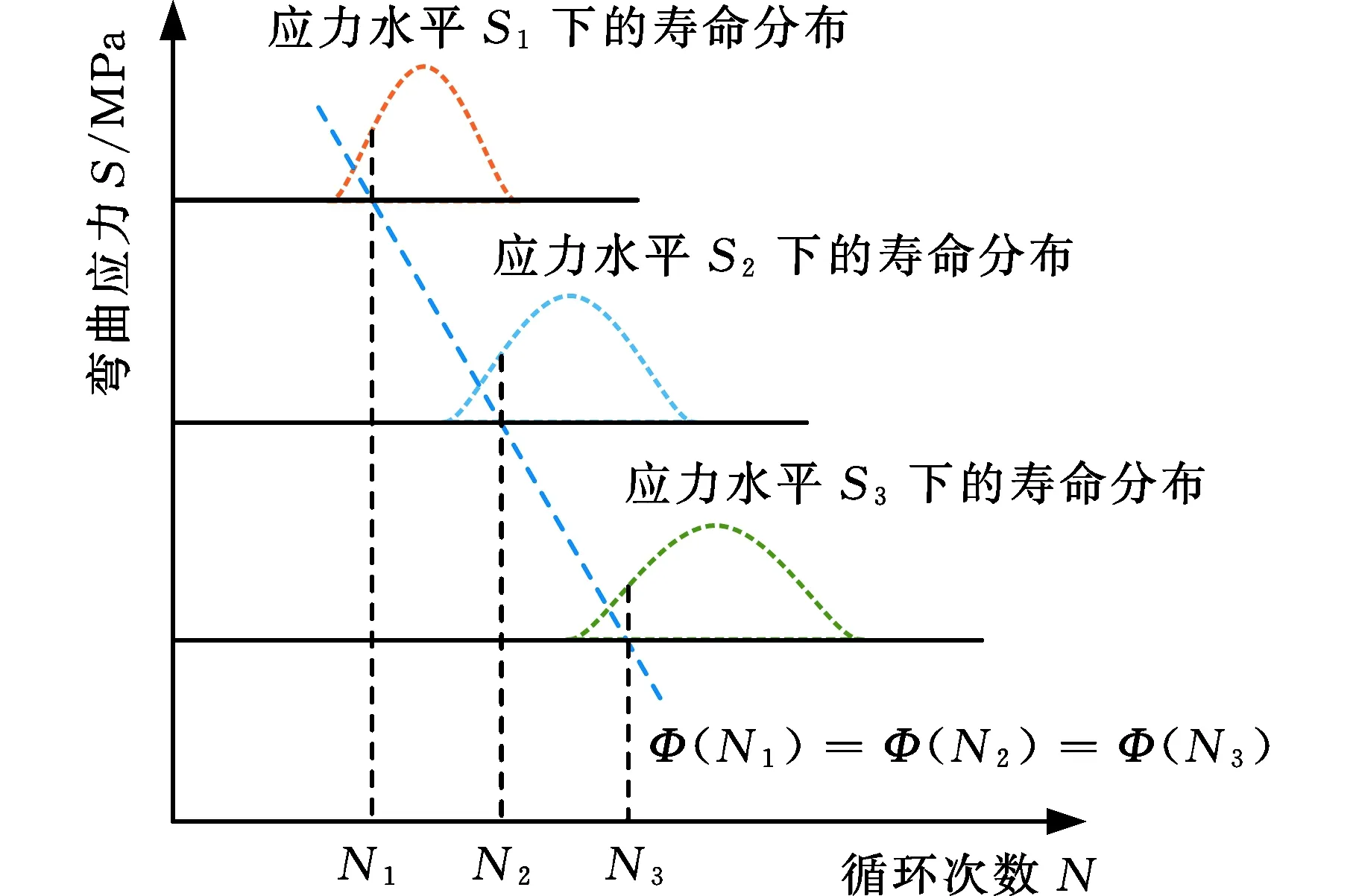
图3 P-S-N曲线拟合原理图Fig.3 P-S-N curve fitting principle diagram

2.2 基于分层贝叶斯模型的P-S-N曲线拟合

从贝叶斯统计的观点来看，模型参数也被看作是具有概率分布的随机变量[23]。分层贝叶斯方法(hierarchical Bayesian model，HBM)相对于经验贝叶斯方法的优势在于分层先验中包含了模型参数的结构信息[24]，同时避免了超参数的选择，能够提供一种更具鲁棒性的分析手段。本文将齿轮弯曲疲劳寿命数据建模分为两个层次，如图4所示，一个层次是指每个应力水平下的疲劳寿命，另一个层次是不同的应力水平下的疲劳寿命。HBM模型将各应力级下疲劳寿命参数分布估计与S-N曲线的线性拟合同时进行，并将计算应力水平之外的疲劳寿命分布信息考虑在内，以进行数据的融合与交换，从而获取最优拟合结果。

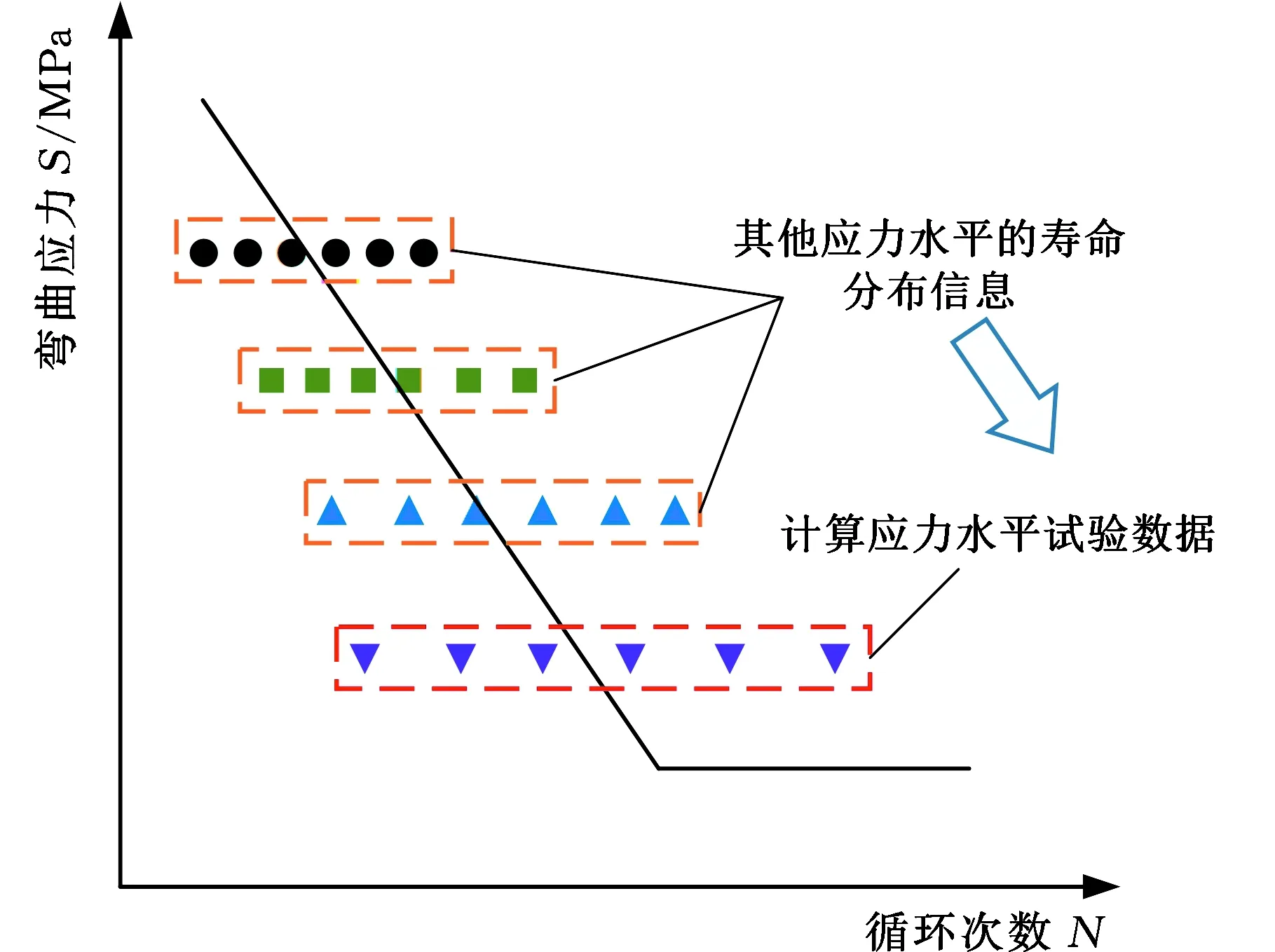
图4 分层贝叶斯模型估计S-N曲线示意图Fig.4 Schematic diagram of S-N curve estimated byhierarchical Bayesian model

本文中齿轮弯曲疲劳S-N曲线采用目前最为常用的Basquin模型，若考虑各应力水平下疲劳寿命的随机性，则Basquin方程可表达为

(4)

其中，m、C为材料参数；Nj、Sj分别为第j个应力水平下疲劳寿命与应力(j=1,2,…，n;n为应力水平数)；随机变量εj表示在不同应力水平Sj下的随机性，包含材料疲劳特性的不确定性与观测误差。两边同时取对数，可得

lgNj=lgC-mlgSj+δj

(5)

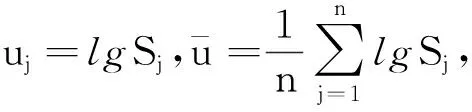
Yj=Xjβ+δj

(6)

Yj=lgNjXj=(1,lgxj)β=(β0,β1)T

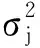
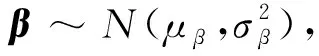
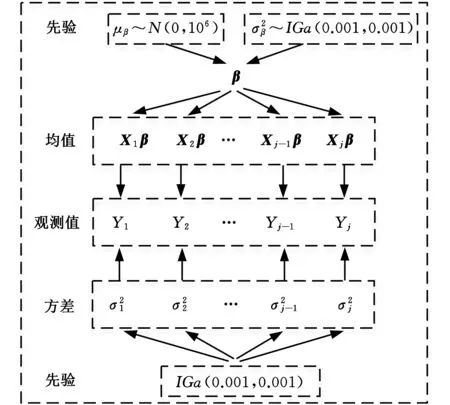
图5 分层贝叶斯层次结构图Fig.5 Hierarchical Bayesian hierarchy diagram

后验分布的计算通常采用数值积分方法求解，马尔可夫链蒙特卡罗(Markov chain Monte Carlo，MCMC)抽样技术[29]中的Gibbs抽样算法适合分层贝叶斯模型，能有效解决高维积分问题[30]，因此本文采用Gibbs抽样算法来求解后验分布。

在样本量较少的情况下，可能存在低应力水平下对数疲劳寿命标准差比高应力水平下对数疲劳寿命标准差小的情形，与目前普遍认为的异方差或同方差理论相悖[31-32]。考虑到本试验中齿轮来自于相同的材料与热处理加工工艺，将不同应力水平下的疲劳寿命分散性用统一的变异系数来度量，以此来表征齿轮材料及加工工艺的一致性。统一的变异系数为

(7)

从而各应力水平下寿命分布的方差可调整为

(8)

2.3 模型的比较与验证

为了验证HBM模型估计P-S-N曲线的性能，将HBM模型与传统LSE模型进行稳定性比较。本节提出了相对斜率指标来进行模型稳定性的比较。假设b0.5表示可靠度为50%下S-N曲线的斜率，b0.99表示可靠度为99%下S-N曲线的斜率，则相对斜率比指标可定义为

(9)

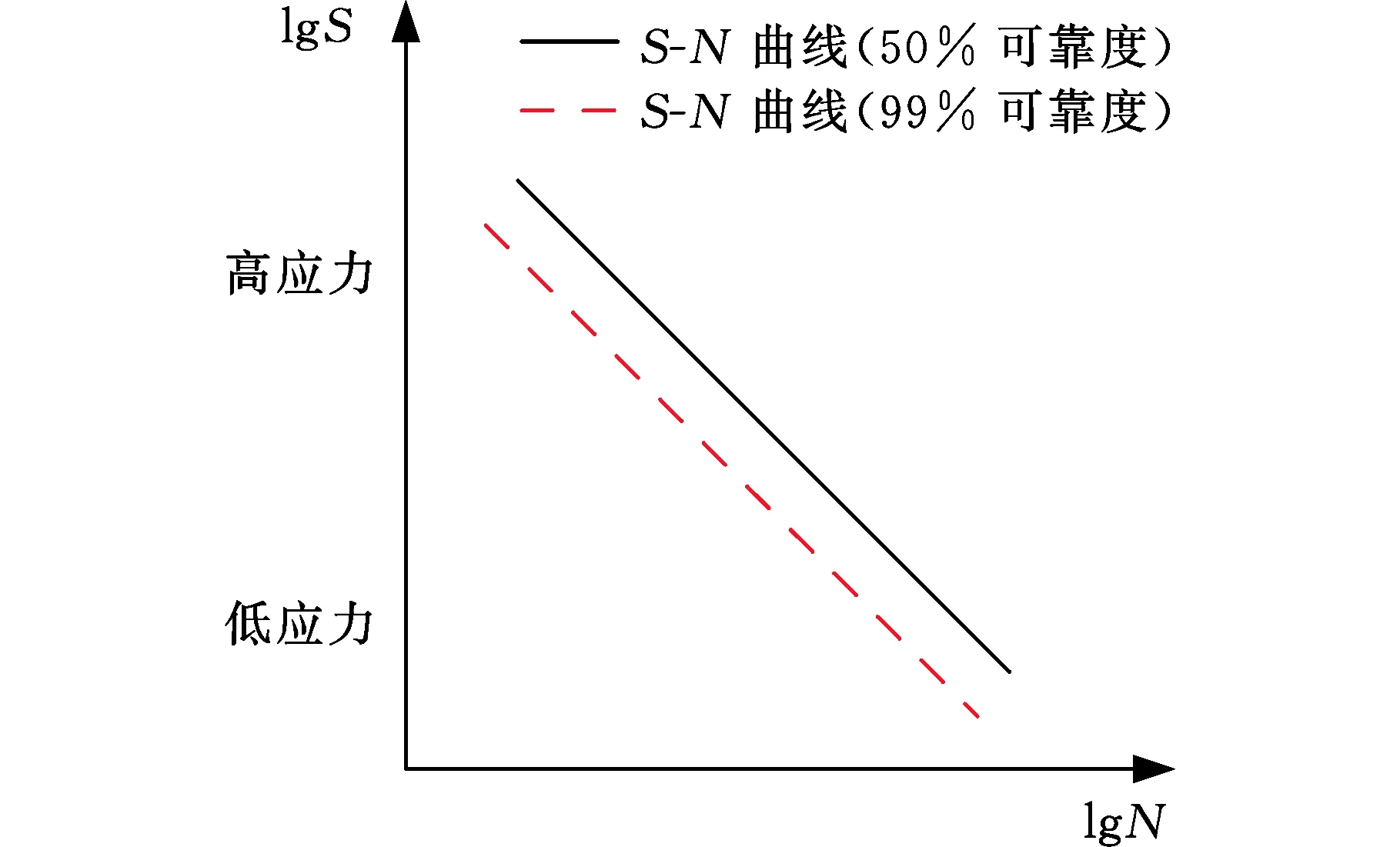
(a)α=1

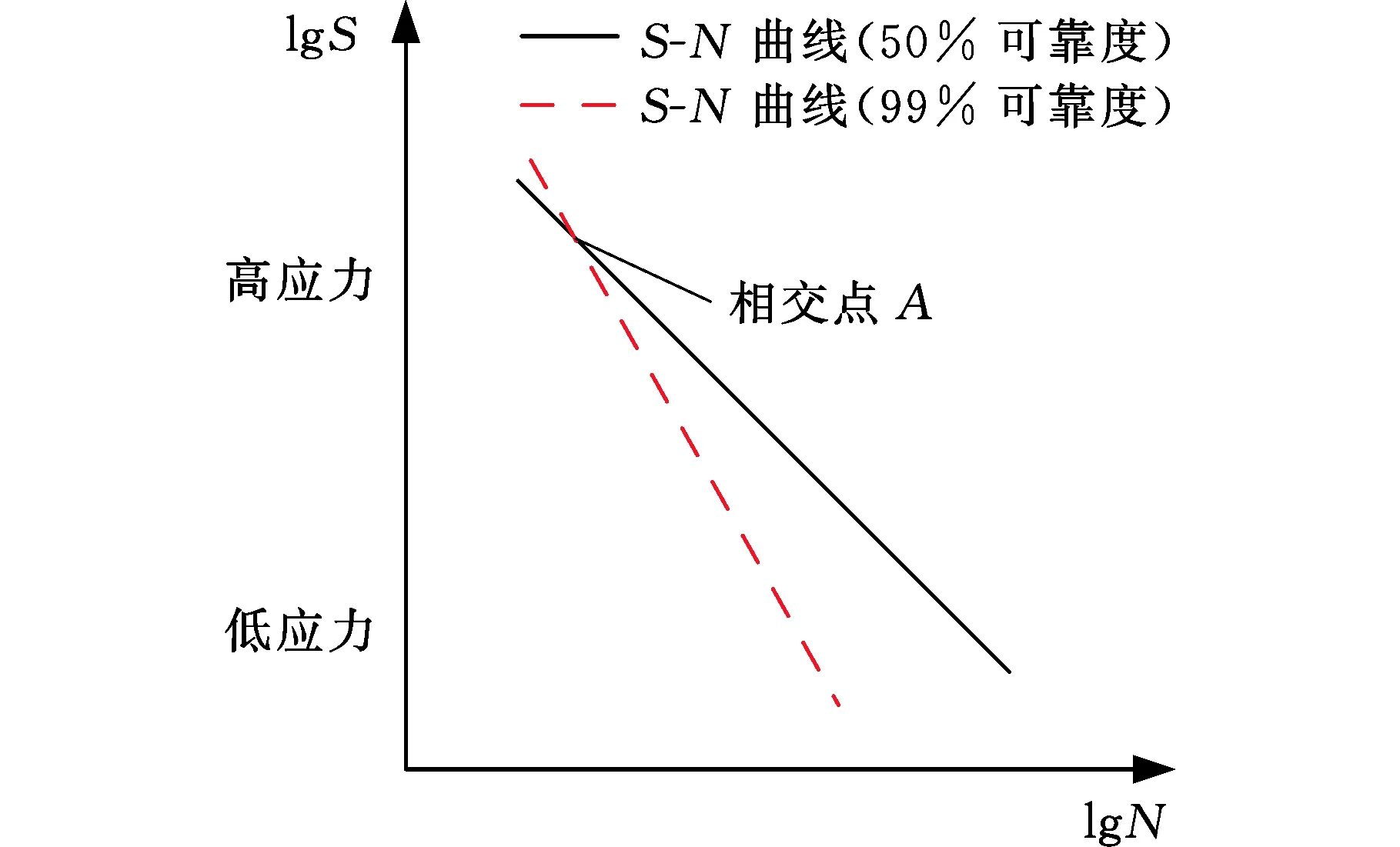
(b)α>1

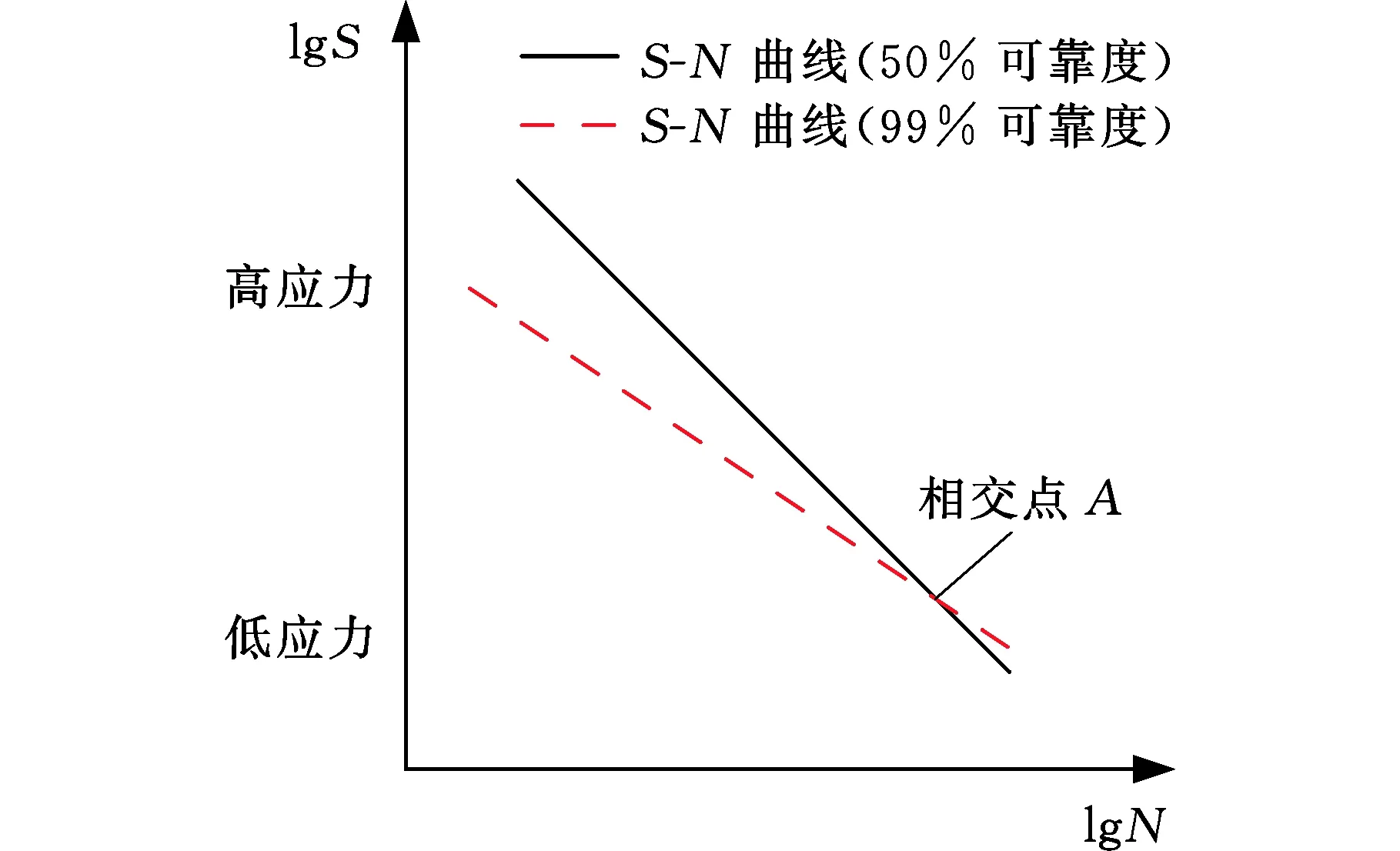
(c)α<1图6 99%可靠度与50%可靠度下S-N曲线的相对位置关系示意图Fig.6 Schematic diagram of the relative positionrelationship of the S-N curve under 99%reliability and 50% reliability

式(9)中的相对斜率比α描述了50%可靠度下与99%可靠度下S-N曲线的相对位置关系，如图6所示。当相对斜率比α=1时，99%可靠度下S-N曲线与50%可靠度下S-N曲线平行，如图6a所示；当相对斜率比α>1时，99%可靠度下S-N曲线与50%可靠度下S-N曲线相交于高应力级下的一点，如图6b所示，该点代表该应力级下试件必定会发生疲劳失效，这与高应力级下易发生弯曲疲劳失效的事实一致；当相对斜率比α<1时，99%可靠度下S-N曲线与50%可靠度下S-N曲线相交于低应力级下的一点，如图6c所示，显然，这与较低应力下存在越出点的事实是相悖的。此时，P-S-N曲线拟合出现失真。因此，可以接受α≥1的情况而不能接受α<1的情况。

3 结果与讨论

本文采用的齿轮弯曲疲劳试验数据，是在4个应力水平(该齿轮弯曲疲劳强度极限约为665 MPa)下进行试验获得的数据，每组试验11次，试验结果见表3。每组11个试验点提供了足够的数据量以作为评价小样本条件下拟合效果的基准。

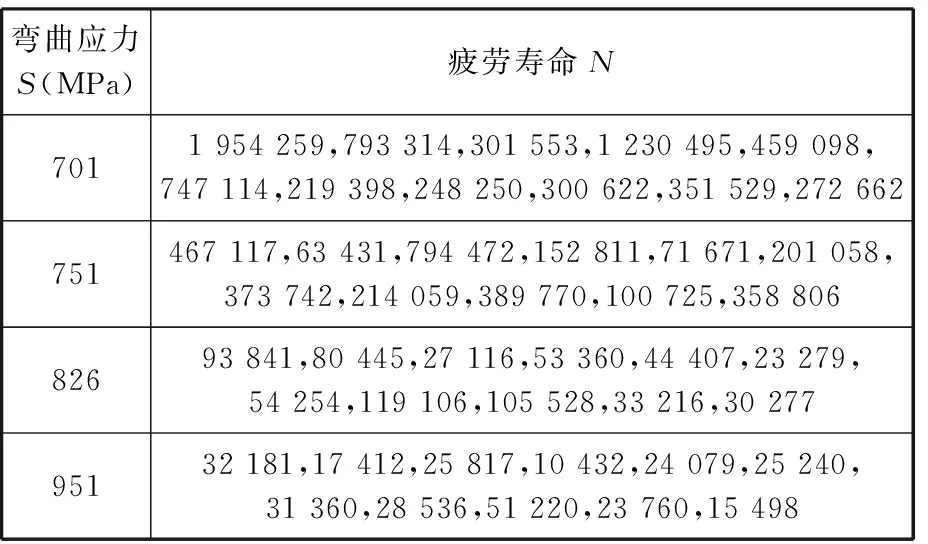
表3 齿轮弯曲疲劳试验结果

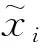
对于“11-11-11-11”(即4个应力级下11个试验点)样本，LSE模型已被证明在大样本情况下有效，因此将其所获得的结果作为基准曲线。由图7a可以看出，HBM模型获得的S-N曲线与LSE模型获得的S-N曲线几乎重合。以相同应力水平下LSE模型的疲劳寿命作为基准，绝对误差计算结果如图7b所示，四个应力级下拟合寿命最大误差为6.10%，表明本文所提出的HBM模型在“大样本数据”情况下具有与LSE模型相同的建模精度。

为对比本文所提出的HBM模型与传统LSE模型统计的稳定性，将疲劳试验数据分为“3-3-3-3”、“5-5-5-5”、“7-7-7-7”、“9-9-9-9”四种样本。在每种测试方案下，用于比较的子数据集都是从表3中完整的数据中进行随机抽样的，每个测试方案下随机抽样104次，表5给出了不同样本量下的统计结果，可以看出，在不同样本量下，本文所提出的HBM模型的相对斜率比α均能给出满意的结果，而传统的LSE模型会出现P-S-N曲线拟合失真的情况。这是因为当疲劳寿命数据不满足随着应力水平逐渐降低而疲劳寿命方差逐渐增大的规律时，传统的LSE模型不能给出满意的拟合结果，而本文所提出的模型稳定性更好而不依赖于数据样本本身。

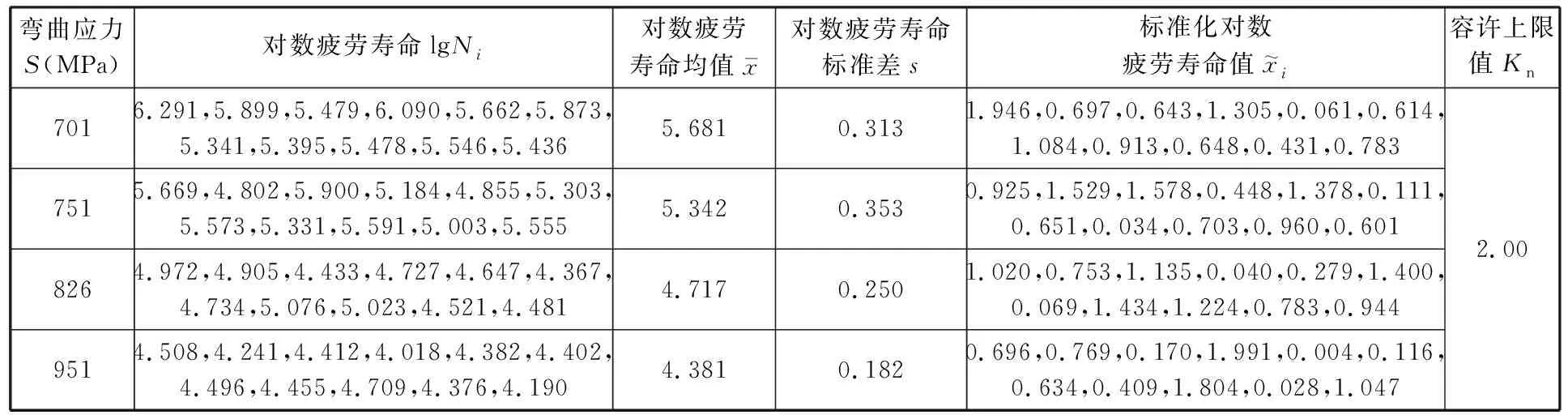
表4 齿轮弯曲疲劳试验数据预处理

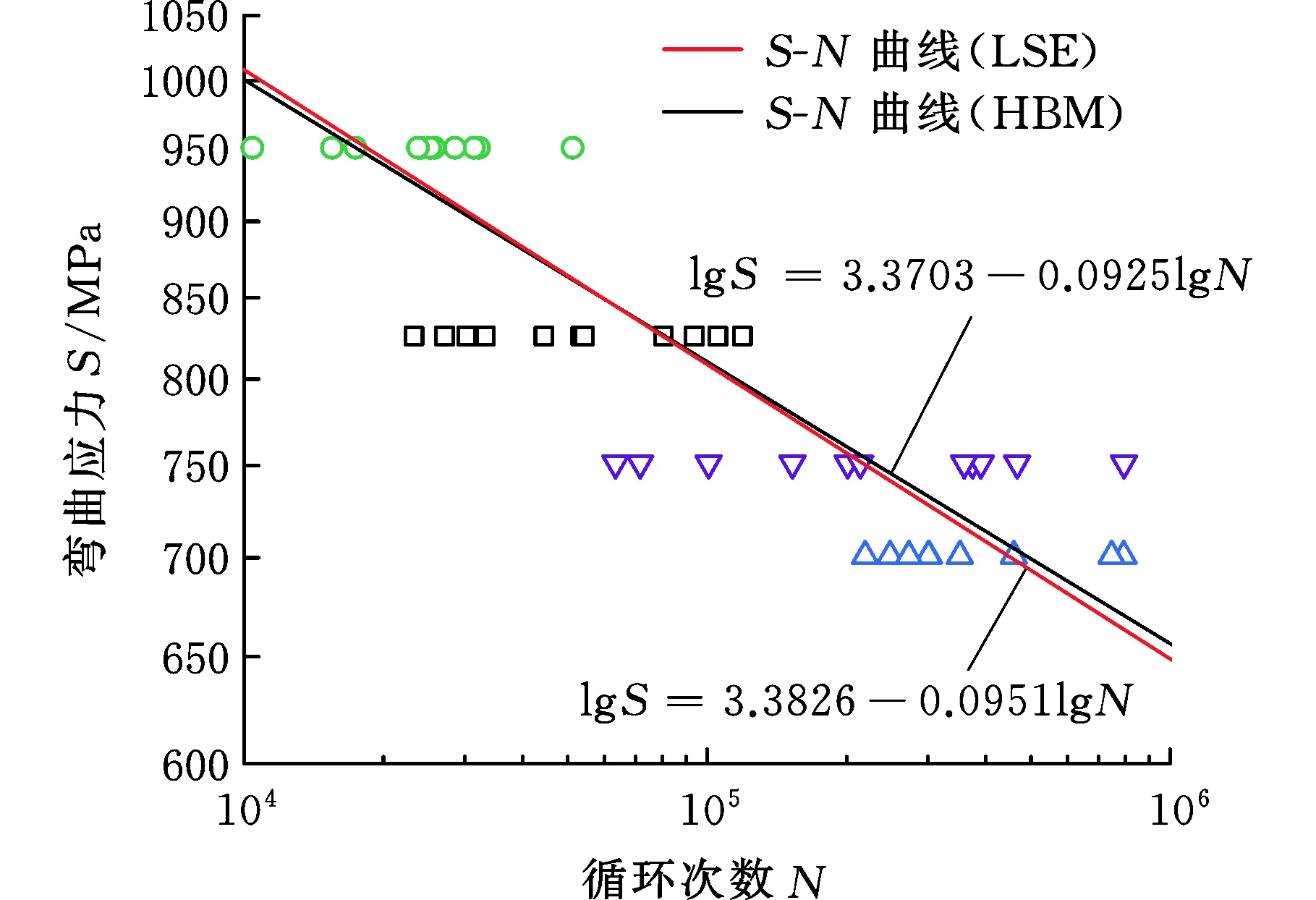
(a)50%可靠度下S-N曲线

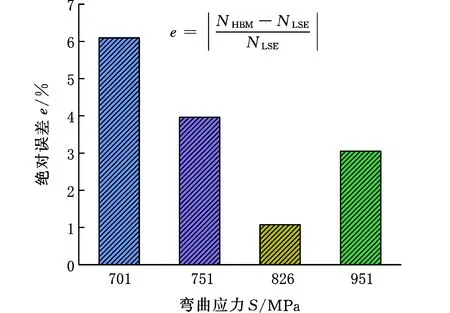
(b)拟合寿命绝对误差图7 11-11-11-11样本量下50%可靠度下S-N曲线与每个应力水平寿命的误差Fig.7 The error between the S-N curve and the lifeof each stress level at 50% reliability under 11-11-11-11sample size

其次，LSE与HBM模型相对斜率比α波动范围均随样本量增加而减小，但本文所提出的HBM模型波动范围较小。随着样本量的变化，LSE模型最小波动范围为0.7869，是本文所提出的HBM模型最大波动范围(即0.2213，样本量为“3-3-3-3”)的3.6倍左右。显然，与传统的LSE模型相比，本文所提出的HBM模型具有更好的稳定性。

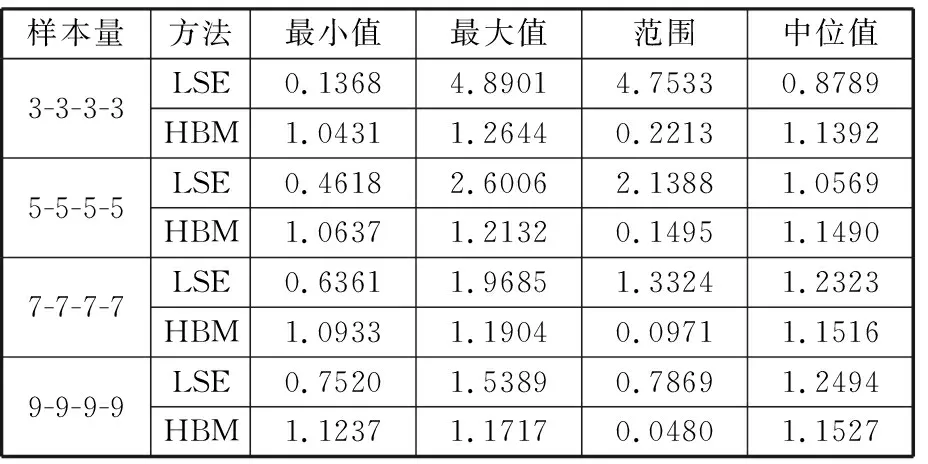
表5 不同样本量下的相对斜率比α值

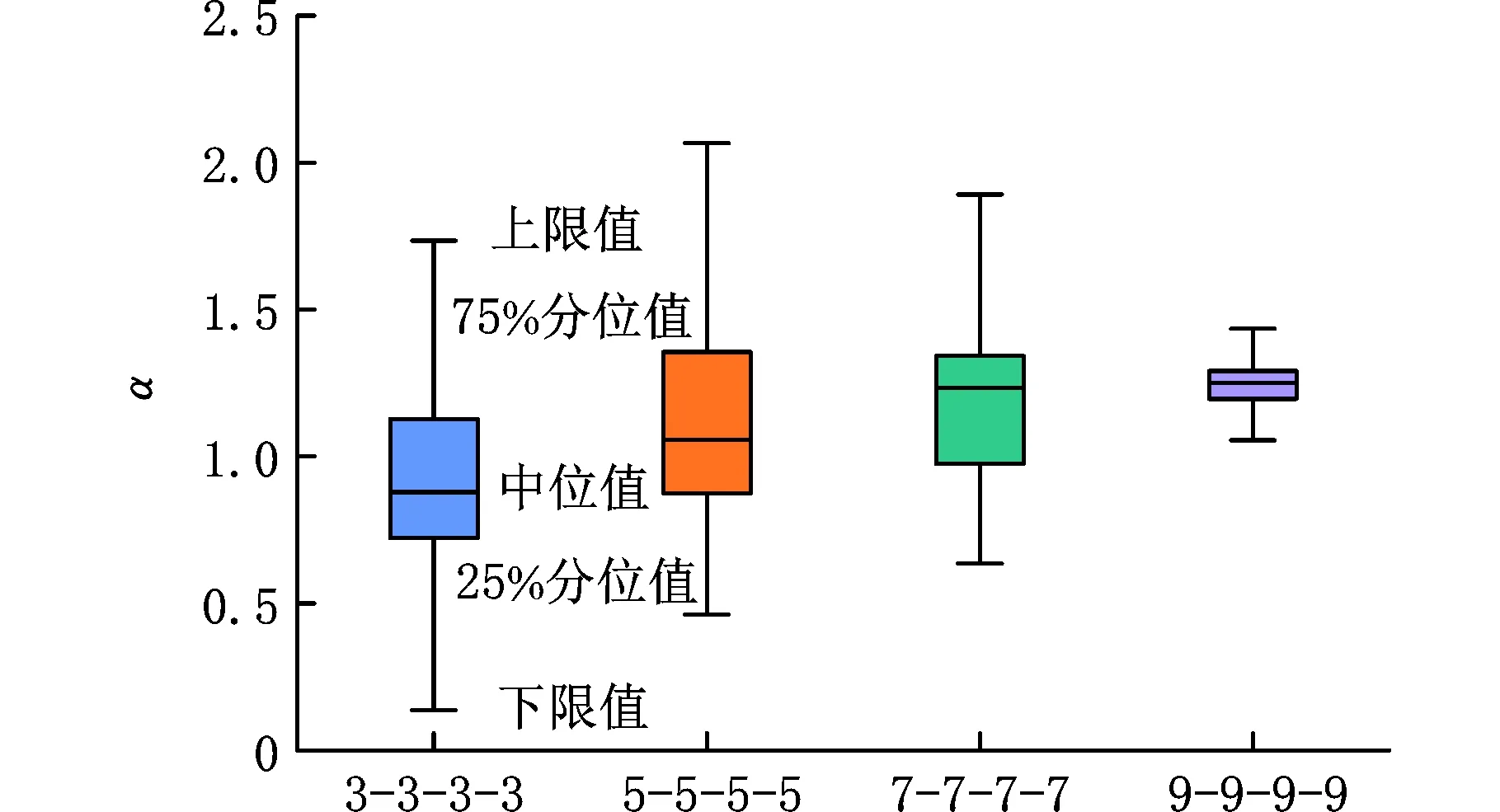
(a)不同样本量下LSE模型α值

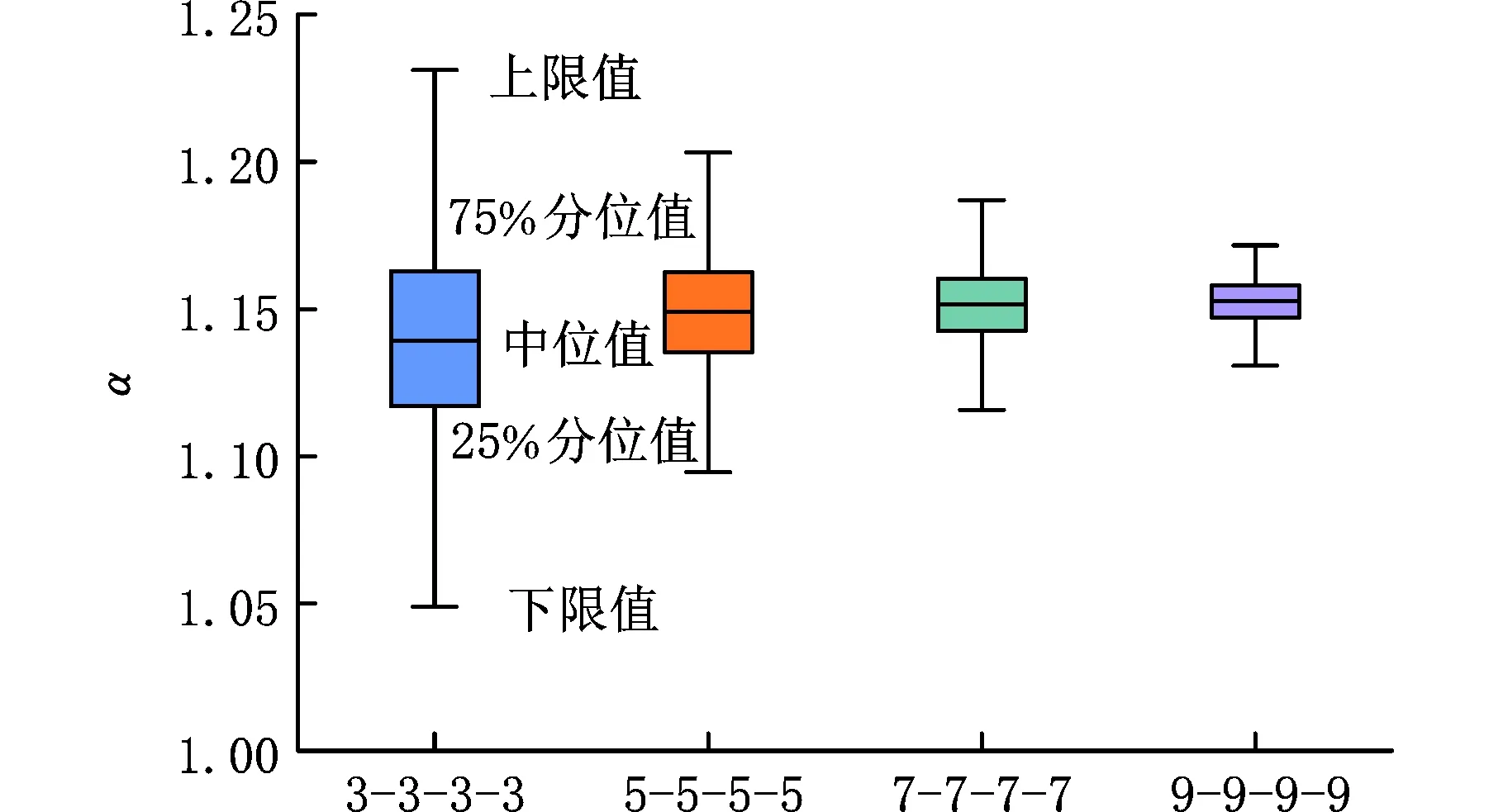
(b)不同样本量下HBM模型α值图8 不同样本量下LSE与HBM模型α值Fig.8 LSE and HBM model α values under differentsample sizes

由图8a和图8b中的箱型图可以看出，随着样本量的变化下，本文提出的HBM模型相对斜率比α均大于1，而LSE模型在样本量为“3-3-3-3”和“5-5-5-5”时易出现拟合失真的情况。当样本量从“3-3-3-3”增加到“9-9-9-9”时，HBM模型相对斜率比α的中位值从1.1392增大到1.1527，变化率为1.19%；而LSE模型中位值从0.8789增大到1.2494，变化率为42.14%。结合目前弯曲疲劳试验数据可知，本文所提出的HBM模型在小样本下拟合效果更佳，不会出现拟合失真的情况。

4 结论

本文开展了齿轮弯曲疲劳试验，并基于齿轮疲劳试验结果提出了用于估计齿轮弯曲疲劳P-S-N曲线的分层贝叶斯(HBM)模型，通过马尔可夫链蒙特卡罗(MCMC)数值仿真得出以下结论：

(1)采用单齿加载方式进行齿轮弯曲疲劳试验，获得了8620H钢渗碳齿轮材料在701 MPa、751 MPa、826 MPa、951 MPa四个弯曲应力级下的弯曲疲劳寿命数据，并建立了HBM模型与LSE模型进行疲劳试验数据的分析与处理。

(2)定义了用于评价P-S-N曲线拟合精度的相对斜率比指标。发现在大样本情况下，HBM模型具有与传统LSE模型相同的建模精度。随着样本量的变化，LSE模型相对斜率比α变化率为42.14%，而本文所提出的HBM模型变化率仅为1.19%，具有更好的稳定性与适应性，为齿轮弯曲疲劳试验等小样本数据场合提供了更具鲁棒性的分析手段。