长期荷载作用对钢-竹组合梁力学性能影响

茅 鸣，童科挺，张家亮，王建民，李玉顺

（1.青岛农业大学 建筑工程学院，山东青岛 266109；2.宁波大学土木与环境工程学院，浙江宁波 315211）

钢-竹组合结构是以竹材人造板和冷弯薄壁“［”形钢为主要材料，通过结构胶、自攻螺钉等复合而成的新型结构体系，可充分发挥竹材与型钢各自的优点.现阶段已对钢-竹组合梁、柱、板等构件进行了一系列短期力学性能试验，并取得了一定成果.长期荷载作用会对钢-竹组合结构的强度、刚度、变形等产生一定影响，故在实际工程应用中，还需考虑长期荷载作用对该类结构力学性能的影响.

目前的建筑结构中，仍以混凝土、钢-混凝土组合构件使用较为广泛，国内外学者对型钢混凝土［1］、钢管混凝土［2-3］、钢板混凝土［4］等组合构件在长期荷载作用下的力学性能进行了诸多试验研究.韩林海等［5-8］通过试验和理论分析，研究了长期荷载作用对矩形钢管混凝土柱、夹层钢管混凝土柱（CFDST）、矩形空心截面钢管混凝土柱变形和承载力的影响，在分析了长期荷载水平、长细比、材料强度等因素影响的基础上，分别提出了相对应的承载力简化计算公式.李达等［1］推导了考虑收缩徐变和界面滑移的型钢-混凝土组合梁长期挠度计算公式，并利用FLAC3D软件进行变形模拟，对公式计算、试件工程测量和软件模拟的数据进行对比分析，结果表明该研究方法可用来计算型钢-混凝土组合梁长期变形.Ding等［9］、曹万林等［10-11］对再生混凝土足尺梁进行长期稳定加载，探讨了不同持荷水平、不同骨料取代率对梁挠度和徐变系数的影响并进行了非线性拟合分析，得到的计算值与试验值较为吻合.Dall’Asta等［12］、Xue等［13］对预应力钢-混凝土组合梁进行长期加载试验，探究了混凝土蠕变、收缩及预应力筋松弛等综合效应对组合梁变形及受力状态的影响.李玉顺等［14］对若干重组竹试件进行长期荷载作用下的拉伸与压缩蠕变试验，研究重组竹在不同应力水平下的蠕变特点及变化规律，通过Burgers模型和Findley幂律模型对蠕变曲线进行拟合，确定了重组竹蠕变模型.刘非微［15］研究了不同长期荷载水平作用下旋切板胶合木（LVL）梁的蠕变变形发展规律，并在长期持荷110 d后对LVL梁进行受弯性能试验，根据试验曲线拟合不同本构模型中的蠕变系数，确定了适用于LVL梁的最佳蠕变本构方程.Amino［16］研究了长期作用下竹木复合梁所能允许的荷载水平、蠕变变形及受弯性能.

在钢-竹组合结构方面，刘欣荣等［17-18］对钢-竹组合柱实施长期加载试验，分析了其蠕变特性以及经历长期荷载后的轴心受压力学性能；周佳如等［19］研究了钢-竹组合楼板在经历长期荷载作用后的力学性能变化，并提出了长期刚度建议公式和挠度计算方法；李玉顺等［20］探究了长期荷载作用对钢-竹界面承载力、黏结应力、相对滑移的影响.但是，对于组合梁在长期荷载作用下的力学性能尚未有深入研究，故本文在组合梁短期破坏试验的基础上，对钢-竹组合工字形梁进行了长期荷载作用下的力学性能试验.通过短期、长期试验的对比，研究长期荷载作用对组合梁极限承载力、挠度变形、构件延性、截面应变等方面的影响，并提出经历长期加载后的组合梁挠度、承载力计算公式，以期为钢-竹组合梁在实际工程中的应用提供理论基础.

1 试验概况

1.1 试件设计

试验共设计了12根钢-竹组合工字形梁试件，如图1（a）所示.在制作时首先通过按1∶1质量比搅拌的A、B环氧树脂胶将2块冷弯薄壁“［”形钢粘贴于腹板（竹胶板）两侧形成腹板骨架，然后在腹板骨架上下翼缘处分别粘贴竹胶板，形成工字形截面的组合梁，如图1（b）所示.其中6根组合梁（DL-1～DL-6）直接进行受弯破坏试验，称其为短期一次破坏试验；剩余6根组合梁（CL-1～CL-6）以0.6倍正常使用极限状态下的荷载值作为长期加载的荷载水平，进行长期加载试验，然后再对其进行受弯破坏试验，称其为长期荷载作用后的二次破坏试验.试件长度均为2.6 m，计算跨度为2.4 m；以截面翼缘竹胶板厚度tw、钢板厚度ts以及含钢率（体积分数）为主要参数.具体试验参数如表1所示.

图1 钢-竹组合工字形梁Fig.1 Steel-bamboo combination I-section beam

表1 试件基本参数Table 1 Parameters of specimens

试件由竹胶板和冷弯薄壁“［”形钢通过结构胶粘结而成；根据GB/T 17657—2013《人造板及饰面人造板理化性能试验方法》及GB/T 228.1—2010《金属材料拉伸试验第一部分：室温试验方法》，分别对2种材料进行静曲试验和拉伸试验，以测定竹胶板的静曲强度MOR、弹性模量Eb，以及钢材的屈服强度fy、抗拉强度ft、弹性模量Es和屈强比fy/ft.材性实测结果如表2、3所示.

表2 竹胶板力学性能Table 2 Mechanical properties of bamboo plywood

表3 薄壁钢板力学性能Table 3 Mechanical properties of thin-walled steel

1.2 长期加载试验

本试验综合重物加载与机械加载2种方式的优点，通过一种自制的自平衡长期加载装置（已获国家发明专利授权ZL 201410809159.8）进行加载，加载装置实物图和示意图如图2、3所示.长期加载的荷载等级取组合梁0.6倍正常使用极限状态下的荷载值.试验从春季开始，经历1 a完整的四季循环.

图2 长期加载装置实物图Fig.2 Image of long-term loading device

1.3 受弯试验方案

一次破坏试验和二次破坏试验均通过自带荷载传感器的液压千斤顶和分配梁进行加载，实现2点对称集中荷载加载模式，加载装置如图4（a）所示.试验采用力控制分级加载方式，其中试件DL-1～DL-4、CL-1～CL-4每级 加载2 k N；试件DL-5和DL-6、CL-5和CL-6每级加载4 k N，试验数据需在每级加载稳定后采集，以保证试验精度.

为测得组合梁跨中截面应变变化，在梁跨中腹板处钢板表面以及上、下翼缘钢板与竹胶板表面均布置若干应变片.沿梁长方向共设置7个百分表，以确定组合梁在荷载作用下的整体变形情况，见图4（b）.

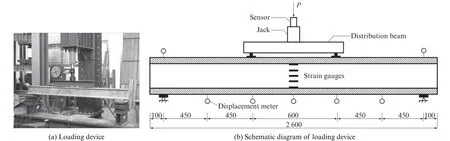
图4 受弯试验加载装置Fig.4 Loading device for bending test（size：mm）

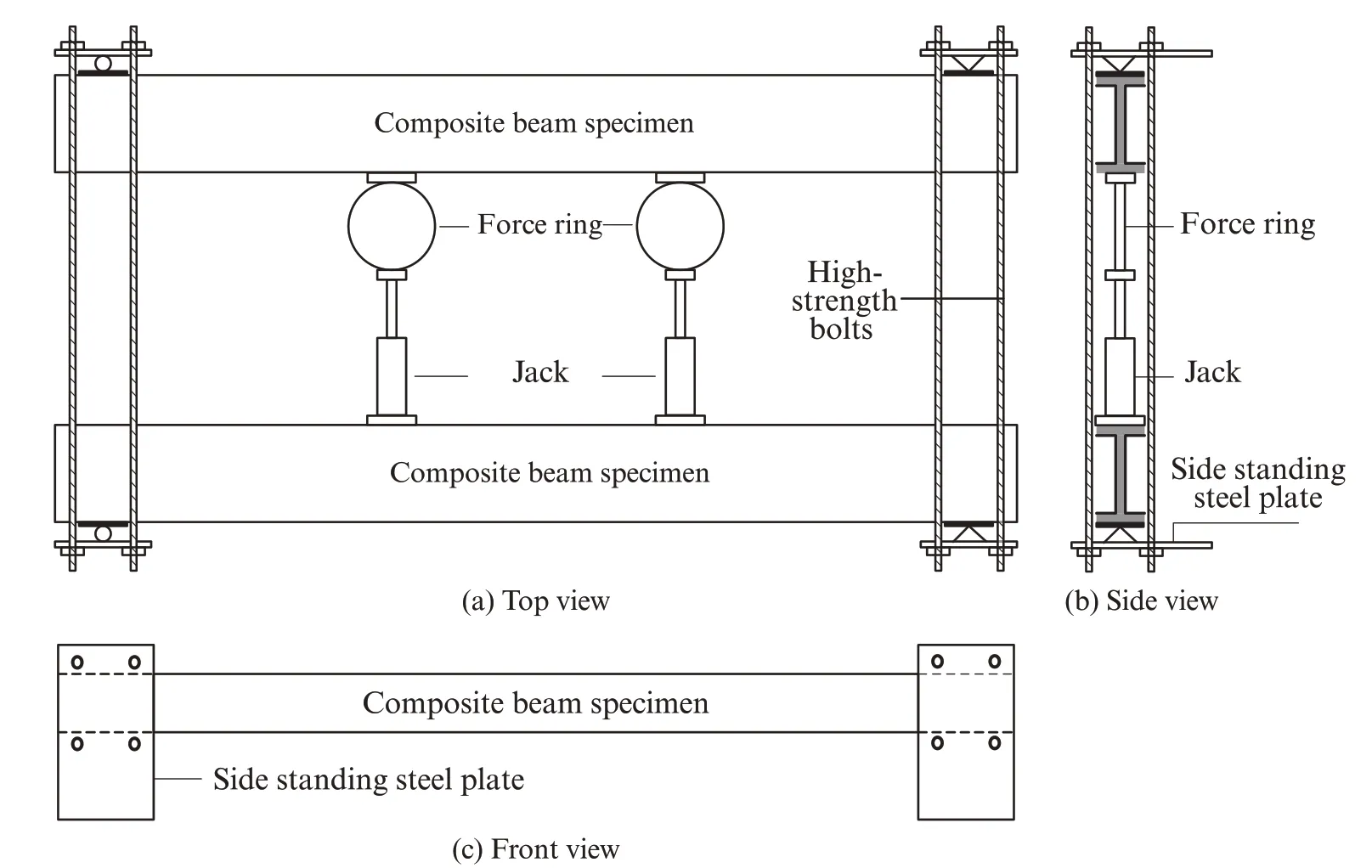
图3 长期加载装置示意图Fig.3 Schematic diagram of long-term loading device

2 试验结果及分析

2.1 短期一次破坏试验现象

短期一次破坏试验共6个试件，由于竹胶板厚度、冷弯薄壁钢板厚度以及含钢率等参数差异，试件在受力过程中表现出一定的统一性和差异性.

在加载初期，各试件的破坏现象及其发展过程基本类似；在加载到50%～60%破坏荷载时，开始出现细微的脱胶声及竹材开裂声；随着荷载增加，翼缘竹胶板开始出现裂缝，加载点附近钢板下凹，发生局部屈曲；最终各试件由于参数差异等影响出现不同的破坏形态.试件DL-1和DL-2由于下翼缘竹胶板出现层间撕裂、钢-竹界面发生细微脱胶而破坏，见图5（a）、（b）；试件DL-3～DL-6由于加载点处翼缘钢板屈曲严重，上翼缘竹胶板开胶掀起而破坏，其中试件DL-4和DL-5的下翼缘竹胶板出现了少许的撕裂，见图5（c）～（f）.

图5 一次破坏试验现象Fig.5 One-time destruction test phenomenon

从整体分析，一次破坏试验现象主要与组合梁含钢率有关.含钢率较低时，组合梁一般表现为下翼缘竹胶板脱胶开裂；随着含钢率的增加，组合梁破坏现象逐渐向上部转移，破坏时上翼缘集中力作用处钢板开始局部屈曲，上翼缘竹胶板掀起，部分试件上、下翼缘均出现竹胶板脱胶开裂现象.

2.2 长期二次破坏试验现象

对经过1 a长期加载的6个组合梁试件进行二次破坏试验.通过对试件二次破坏现象的分析，发现二次破坏试验现象与一次破坏试验现象基本一致，具有较为相同的破坏规律.但最终破坏时，组合梁上、下翼缘均出现不同程度的脱胶、掀起开裂，说明长期荷载作用使组合梁出现了一定程度的初始损伤.

以试件CL-1和CL-5为例.试件CL-1在加载至30.4 k N时，组合梁开始发出声响，此时跨中挠度为16.56 mm；当荷载增至39.4 kN时出现持续撕裂声，组合梁下翼缘脱胶（见图6（a））、上翼缘掀起（见图6（b）），此时停止加载.试件CL-5加载至40.6 k N时出现细微脱胶声，加载点处翼缘出现细微脱胶，此时跨中挠度为14.53 mm；当荷载增至59.5 k N时发出连续开裂声，竹胶板出现纵向裂缝；加载至72.2 kN时，脱胶面逐渐扩大，加载点开胶处翼缘钢板屈曲变形（见图6（c）），随后竹胶板裂缝进一步发展、翼缘竹胶板层间开裂显著（见图6（d）），因试件丧失承载力而结束试验.

图6 二次破坏试验现象Fig.6 Second destruction test phenomenon

2.3 荷载-跨中挠度曲线

组合梁一、二次破坏试验的荷载-跨中挠度（P-um）关系曲线如图7所示.比较图7（a）、（b）的发展趋势可以发现，一次破坏试验与二次破坏试验的荷载-跨中挠度曲线变化趋势略有不同.经历长期荷载作用后，组合梁弹性阶段与弹塑性阶段区分更加明显，进入弹塑性阶段后试件整体刚度有所下降，荷载-跨中挠度曲线斜率显著减小，说明经过长期荷载作用的试件产生了更大挠度.以试件DL-5、CL-5和试件DL-6、CL-6为例（见图8（a）、（b）），加载初期，试件DL-5与CL-5以及试件DL-6与CL-6的曲线斜率基本相同，曲线在弹性阶段基本重合；随着组合梁屈服，该关系曲线开始分离，二次破坏试件CL-5、CL-6挠度变化加快，曲线斜率更小.最终破坏时，二次破坏试验的组合梁极限荷载略小于一次破坏试验的相应值.

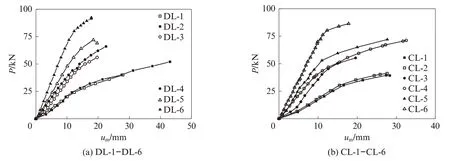
图7 一、二次破坏试验的荷载-跨中挠度关系曲线Fig.7 Load-midspan deflection curves for first and second failure tests

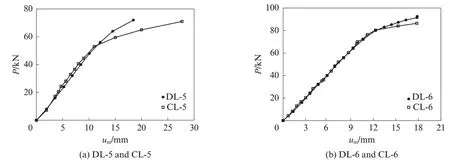
图8 一、二次破坏试验的荷载-跨中挠度关系对比曲线Fig.8 Load-midspan deflection relation comparison curves for first and second failure tests

2.4 荷载-应变曲线

图9为试件DL-6和CL-6的跨中截面应变变化曲线.对比分析图9（a）、（b）可得：（1）加载过程中，跨中截面应变沿高度方向呈线性分布，符合平截面假定.后期由于界面滑移，应变曲线在钢-竹交界面处出现折点.在组合梁破坏时，二次破坏试件CL-6的应变与一次破坏试件DL-6相比明显增大，说明长期荷载作用对组合梁的力学性能产生了一定影响，降低了组合梁的整体刚度.（2）组合梁在长期荷载作用前后，中性轴位置并没有发生明显变化，仍然保持在组合梁中间位置，可见竹胶板长期受拉或受压对组合梁的影响基本相同，并未改变组合梁中性轴位置.

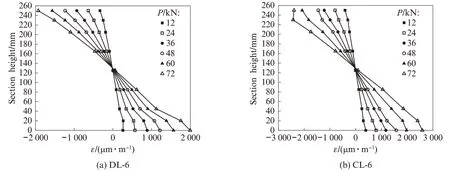
图9 一、二次破坏试验的跨中截面应变关系曲线Fig.9 Strain relationship curves of midspan section for first and second failure tests

2.5 极限荷载

通过一次破坏试验和二次破坏试验获得的极限荷载值FuDL、FuCL及其对比，以及通过一、二次破坏试验的正常使用极限荷载值F′uDL、F′uCL及其对比如表4所示.由表4可见：经过二次破坏试验后，截面尺寸及含钢率较小试件CL-1、CL-2的正常使用极限荷载F′uCL有了较为显著的降低；随着截面尺寸及含钢率的提高，一、二次破坏试验的正常使用极限荷载F′u相差不大，两者比值均在3%以内.由此可见，长期荷载作用对截面尺寸及含钢率较大试件在正常使用阶段的力学性能影响并不明显.在承载能力极限状态下，除试件CL-4外，其余二次破坏试件的极限荷载均有不同程度的减小.原因是试件DL-4在荷载达到66 k N后仍能继续加载，但荷载作用处竹胶板开裂，钢板局部屈曲，因此认为该试件已达到极限承载能力而结束试验，导致在最终统计极限荷载值时，其一次破坏试验的极限荷载略低于二次破坏试验的相应值.

表4 一、二次破坏试验的极限荷载Table 4 Ultimate load for first and second failure tests

3 理论分析

3.1 跨中挠度

试验表明，长期加载对组合梁在正常使用极限状态下的挠度变化影响不大，而进入弹塑性阶段后，组合梁刚度明显减小.本文基于有效惯性矩法［21-23］对组合梁破坏时的挠度进行计算研究.由组合梁的荷载-跨中挠度发展曲线可以发现，该曲线发展趋势大致呈两折线，即为钢-竹组合梁受力过程中的弹性阶段和弹塑性阶段.每个阶段内，荷载与挠度基本呈线性关系，所以跨中挠度δ（即um）与跨中弯矩M也是线性关系：

沿梁长方向的有效惯性矩I可用下式定义：

式中：k是由Eb、跨径和荷载类型确定的常数；x、y值均可以根据边界条件求得.

（1）弹性阶段（M≤Mcr），此时认为有效惯性矩为常量，即：

（2）弹塑性阶段（Mcr＜M＜Mu），此时有效惯性矩，可简化为：

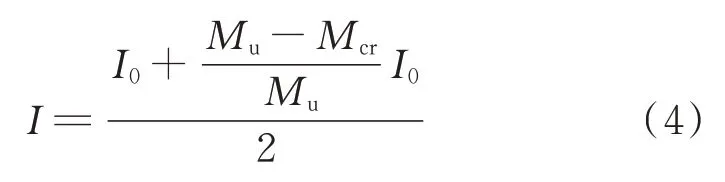
式中：Mcr、Mu分别为一次破坏试验中，钢板屈服时和承载力极限状态下的跨中弯矩.

根据有效惯性矩法以及组合梁经历长期荷载作用后的变形模量变化，结合考虑滑移作用［24］，可得到经历长期荷载作用后的组合梁挠度计算公式.

（1）弹性阶段（M≤Mcr）：

（2）弹塑性阶段（Mcr＜M＜Mu）：

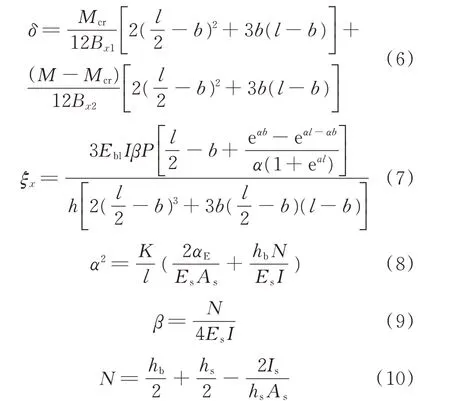
式中：Bx为考虑滑移效应影响时组合梁的折减刚度，，由于组合梁在经历长期荷载作用后会产生残余变形，若加入计算会相当复杂，故简化认为弹性阶段其弹性模量未发生改变，即为集中力到跨中的距离；l为组合梁计算跨度；Eb、Es分别为竹胶板和钢板的弹性模量；Ebl为经历长期荷载作用后的竹胶板弹性模量，Ebl＝Eb/（1＋χϕ），其中χ为调整系数，ϕ为竹胶板蠕变系数；As为钢板截面积；αE为钢板与竹胶板的弹性模量之比；hb为翼缘竹胶板高度；hs为钢板截面高度；K为结构胶抗剪刚度［25］.

以试件CL-4和CL-6为例，它们在每级弯矩荷载作用下的跨中挠度理论计算值与试验值如表5所示.由表5可知，2个试件的理论计算结果与试验结果均吻合较好，误差基本在10%以内，且挠度试验值小于理论计算值，具有一定的安全性.

表5 组合梁挠度试验值与理论值Table 5 Test value and theoretical value of composition beam deflection

3.2 承载力

为方便计算与分析，采用叠加法进行组合梁承载力计算，并作出如下假设：

（1）组合梁二次破坏试验时的竹胶板应力σ′b与短期一次破坏试验时的竹胶板应力σb成比例，即σ′b＝λσb.

（2）组合梁界面不发生滑移.

组合梁极限承载力（即跨中截面所能承受的最大弯矩）为：

则长期加载后的组合梁极限承载力为：

承载力衰减可表示为：

式中：Mb为组合梁中竹胶板的正截面抗弯承载力，Mb＝γbσbWb（其中γb为组合梁中竹胶板截面强度折减系数，取0.95；Wb为组合梁中竹胶板的截面模量）；Ms为组合梁中钢板的正截面抗弯承载力，Ms＝γsfsWs（其中γs为组合梁中薄壁钢板截面塑性发展系数，取1.05；fs为破坏时薄壁钢板的抗拉强度；Ws为组合梁中薄壁钢板的截面模量）.

3.2.1 竹胶板厚度

仅增大竹胶板厚度，即Ms保持不变，则式（13）可化简为：

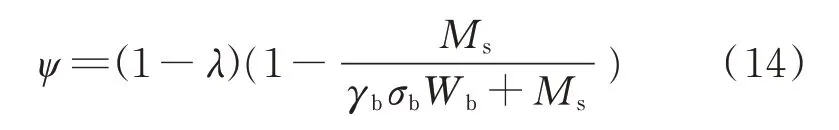
由式（14）可知，ψ与竹胶板厚度呈正相关，竹胶板越厚，承载力衰减越大；若竹胶板厚度远大于钢板厚度，则可将组合梁视为竹梁，此时其承载力约为原极限承载力的λ倍.

试件DL-1与DL-2（包括CL-1与CL-2）的不同之处仅在于竹胶板厚度（分别约16、18 mm）.由表4可知：对于二次破坏试件而言，CL-2（竹胶板厚度约18 mm）的极限荷载值相比CL-1（竹胶板厚度约16 mm）提高了1.8 k N；对于一次破坏试件而言，DL-2（竹胶板厚度约18 mm）的极限荷载值相比DL-1（竹胶板厚度约16 mm）提高了12.0 kN.对比一、二次破坏试件DL-1与CL-1（包括DL-2与CL-2）的极限荷载值可知，CL-1较DL-1降低了0.6 k N，而CL-2较DL-2降低了10.8 k N.由此可见，竹胶板厚度增加对组合梁自身承载力有一定的提高作用，但组合梁承载力的衰减程度随着竹胶板的增厚而显著增大.

3.2.2 钢板厚度

仅改变钢板厚度，即保持Mb不变，则式（13）可简化为：

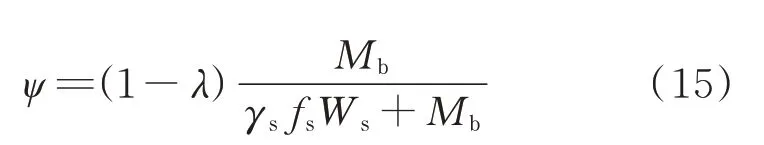
由式（15）可以发现，ψ与钢板厚度呈负相关，钢板越厚，承载力衰减越小，当竹胶板厚度远小于钢板厚度时，可认为组合梁为钢梁，此时其承载力衰减为0.

以钢板厚度不同、竹胶板厚度相同的组合梁试件DL-2与DL-5（包括CL-2与CL-5）为例，其钢板厚度分别为1.5、2.0 mm.由表4可见：对于二次破坏试件而言，CL-5（钢板厚度为2.0 mm）的极限荷载值相比CL-2（钢板厚度为1.5 mm）提高了30.6 kN；对于一次破坏试件而言，DL-5（钢板厚度为2.0 mm）的极限荷载值相比DL-2（钢板厚度为1.5 mm）提高了20.0 k N.对比一、二次破坏试件DL-2与CL-2（包括DL-5与CL-5）的极限荷载值可知，CL-2较DL-2降低了10.8 k N，而CL-5较DL-5降低了0.2 k N.由此可见，钢板厚度的增加使组合梁承载力有了明显提高，且钢板厚度的变化会影响组合梁承载力衰减程度，当钢板厚度增加时，能显著减小组合梁承载力的衰减程度.

3.2.3 含钢率

含钢率受Ab/As影响，若组合梁宽度不变，含钢率可进一步认为受tw/ts影响，则式（13）可简化为：

由式（16）可知，组合梁承载力衰减与Ws/Wb有关，即与Is/Ib成反比，计算过程中简化Ib和Is的计算：

式中：b1为竹胶板宽度；b2为钢板宽度.

由式（17）可以发现，组合梁承载力衰减最终与含钢率和竹胶板厚度有关，可分为以下几种情况：

（1）含钢率保持不变.此时组合梁承载力衰减仅与竹胶板厚度有关.若ts/tw＞1，竹胶板越厚，组合梁承载力衰减越小；若ts/tw＜1，竹胶板越厚，组合梁承载力衰减越大；若ts/tw＝1，则组合梁承载力衰减基本为零.

（2）含钢率增加.若竹胶板厚度增加，此时Is/Ib增加，故组合梁承载力衰减程度不断减小.

（3）含钢率减小.若竹胶板厚度减小，此时Is/Ib减小，故组合梁承载力衰减程度不断增加.

以组合梁试件CL-2与CL-6（包括DL-2与DL-6）为例，其竹胶板厚度分别约18、20 mm，含钢率分别为10%、13%，属于情况（2）、（3）.由表4可见：对于二次破坏试件而言，CL-6（竹胶板厚度约20 mm、含钢率13%）的极限荷载值较CL-2（竹胶板厚度约18 mm、含钢率10%）提高了45.2 k N；对于一次破坏试件而言，DL-6（竹胶板厚度约20 mm、含钢率13%）的极限荷载值较DL-2（竹胶板厚度约18 mm、含钢率10%）提高了40 k N.对比一、二次破坏试件DL-2与CL-2（包括DL-6与CL-6）的极限荷载值可知，CL-2较DL-2降低了10.8 k N，而CL-6较DL-6降低了5.6 kN.由此可见，在含钢率增加，且竹胶板厚度也增加的情况下，可使组合梁承载力有较大程度的提升，且组合梁承载力衰减程度减小，反之则承载力衰减增加，与上述情况相符.

4 结论

（1）一次破坏试验现象与组合梁含钢率有关.含钢率较低时，组合梁一般表现为下翼缘竹胶板脱胶开裂；随着含钢率的增加，组合梁破坏范围逐渐向上部转移，上翼缘集中力作用处钢板出现局部屈曲，部分试件上、下翼缘均出现竹胶板脱胶开裂现象.

（2）长期加载后的二次破坏试验现象与一次破坏现象基本一致，但由于长期荷载作用使组合梁产生了一定程度的初始损伤，导致二次破坏试验的组合梁上、下翼缘均出现脱胶、掀起开裂现象.

（3）长期加载会改变组合梁延性.二次破坏试验的荷载-挠度曲线与一次破坏试验相比，在弹性阶段，2次试验的曲线变化趋势基本一致；进入弹塑性阶段，二次破坏试验的荷载-挠度曲线斜率明显减小.竹胶板长期受拉、压作用对组合梁的影响程度基本相同，组合梁中性轴位置未发生明显改变.

（4）根据有效惯性矩法以及组合梁经历长期加载后的变形模量变化，结合考虑滑移作用，得到了经历长期荷载作用后的组合梁挠度计算公式，由此求出的理论计算值与试验值吻合较好，平均误差在10%以内.

（5）长期荷载作用下，组合梁承载力均有不同程度的下降.承载力衰减与竹胶板厚度、钢板厚度、含钢率有关，其中与竹胶板厚度呈正相关，与钢板厚度呈负相关；含钢率对组合梁承载力衰减程度的影响受竹胶板厚度影响，呈一定规律性变化.