高性能水泥基复合材料断裂性能

徐文磊，宣卫红，陈育志，陈徐东，程熙媛

（1.河海大学土木与交通学院，江苏南京 210098；2.金陵科技学院建筑工程学院，江苏南京 211169）

高性能水泥基复合材料（HPCC）通常由水泥、水、高效减水剂、高强度钢纤维以及细骨料组成，并且具有极低的水灰比.钢纤维在HPCC中通过桥接裂纹面阻止裂纹的发展，使后裂区中发生基体和钢纤维之间的荷载重分布［1］，进而改善高强基体的脆性.已有的研究表明，钢纤维掺量是影响HPCC力学行为的重要因素，拉伸强度、拉伸应变［2］等性能指标对钢纤维掺量具有很大依赖性，但是也有研究发现，钢纤维掺量对弹性模量、第一裂纹对应的抗折强度等无明显影响［3］，钢纤维掺量对HPCC的影响需要进一步的研究.

另外，凭借突出的抗压强度［4］和抗拉强度［5］、高韧性［6］以及高耐久性［7］，HPCC已经成为了重要工程建设中最具前景的建筑材料，例如公路桥梁、高层建筑以及防爆和抗震结构等，这些重要工程对材料抗起裂及裂缝开展后的稳定性和安全性提出了更高的要求.而目前关于HPCC的研究主要集中在机械性能、耐久性能及抗冲击性能等方面，涉及HPCC断裂性能的研究还不多.

Yoo等［8］探究了钢纤维掺量对HPCC弯曲行为的影响，结果表明随着钢纤维掺量的增加，HPCC在峰值载荷下的抗弯强度、挠度和裂缝嘴张开位移（CMOD）呈伪线性增加.卿龙邦等［9］基于线性相关系数陡降法计算了HPCC的起裂韧度，发现当钢纤维体积分数达到0.9%时，定向分布的钢纤维混凝土起裂韧度趋于稳定.邓宗才［10］采用等效断裂韧度方法来评价混杂纤维增强超高性能混凝土的增韧效果.这些研究重点关注了HPCC的一项或者几项断裂性能指标.

本文对钢纤维体积分数为0%、1%和2%的带预制裂缝HPCC矩形梁进行了三点弯曲测试，通过荷载-裂缝嘴张开位移（F-CMOD）曲线分析弯曲强度、残余强度、起裂韧度、失稳韧度、断裂能、脆性指数等随钢纤维体积分数的变化特征.通过扫描电镜（SEM）观察HPCC的断裂面形态，从微观角度进一步分析HPCC的断裂机理.

1 试验

1.1 试验材料和配合比

水泥采用P·Ⅱ52.5硅酸盐水泥，性能符合GB 175—2007《通用硅酸盐水泥》；河砂的最大直径为2.45 mm，细度模数为2.8；聚羧酸盐高效减水剂，固含量为50%（质量分数）；江苏博特新材料有限公司生产的SBT-HDC超细矿物掺和料，其物理性能符合GB/T 18736—2017《高强高性能混凝土用矿物外加剂》；微直钢纤维，长度13 mm，直径0.2 mm，抗拉强度2 800 MPa，以体积分数（φSF）0%、1%和2%添加到HPCC基体中，对应的试件编号为HPCC0、HPCC1和HPCC2.

HPCC的配合比见表1.将搅拌均匀的混合料浇筑在400 mm×100 mm×100 mm的模具中，在（20±2）℃且相对湿度RH＞90%的条件下养护24 h后脱模，于室内自然环境下养护60 d，试验前在试件非成型面中间位置切割深30 mm、宽2 mm的预制裂缝.另外，HPCC0、HPCC1和HPCC2各浇筑3个尺寸为100 mm×100 mm×100 mm的立方体试件，标准养护28 d后进行抗压试验，测得其平均抗压强度分别为64.8、89.8、108.8 MPa.

表1 HPCC的配合比Table 1 Mix proportion of HPCC kg/m3

1.2 三点弯曲测试

采用MTS 322闭环伺服控制系统对试件进行三点弯曲测试.加载方式及试件几何尺寸如图1所示.在预制裂缝两侧各粘贴1个带坡口的铁片安装夹式引伸计，用来测量裂缝嘴张开位移CMOD.试验在CMOD控制方式下进行加载，加载速率为0.001 mm/s，能够稳定获得包括下降段的F-CMOD曲线.每组测试3个试件，编号分别为S1、S2、S3.

图1 加载方式及试件几何尺寸Fig.1 Loading mode and geometry of specimen（size：mm）

1.3 断裂面微观形态分析

通过Hitachi SU 8100型扫描电镜来观察试件断裂面形态，以进一步揭示HPCC的破坏机理.试件弯曲破坏后从断裂面取样，并用无水乙醇浸泡以消除基体水化存在的影响，在进行SEM测试前，将样品置于真空烘箱中干燥24 h.

2 结果与分析

2.1 破坏形态

HPCC试件的破坏形态如图2所示.由图2可见：对于不含钢纤维的试件HPCC0，裂纹一旦萌生很快就会扩展形成宏观裂缝，裂缝从缺口尖端近乎沿直线扩展直达梁顶部，试件完全断裂，断口表面光滑，表现出明显的脆性；在含钢纤维试件的断裂面上可以观察到钢纤维的拔出现象，当裂纹萌生后，裂纹两侧不仅存在基体间的黏聚力，还存在钢纤维的桥接作用，即使达到峰值荷载，试件依旧保持变形和承载能力，裂缝的扩展过程较为缓慢，表现出明显的塑性；相比钢纤维体积分数为1%的试件HPCC1，钢纤维体积分数2%的试件HPCC2裂纹表面粗糙度更大，这是因为在钢纤维体积分数更高的情况下，裂纹表面附近随机分布的钢纤维更多，这些倾斜的钢纤维形成的桥接作用更强，导致基体开裂路径变得更加复杂.

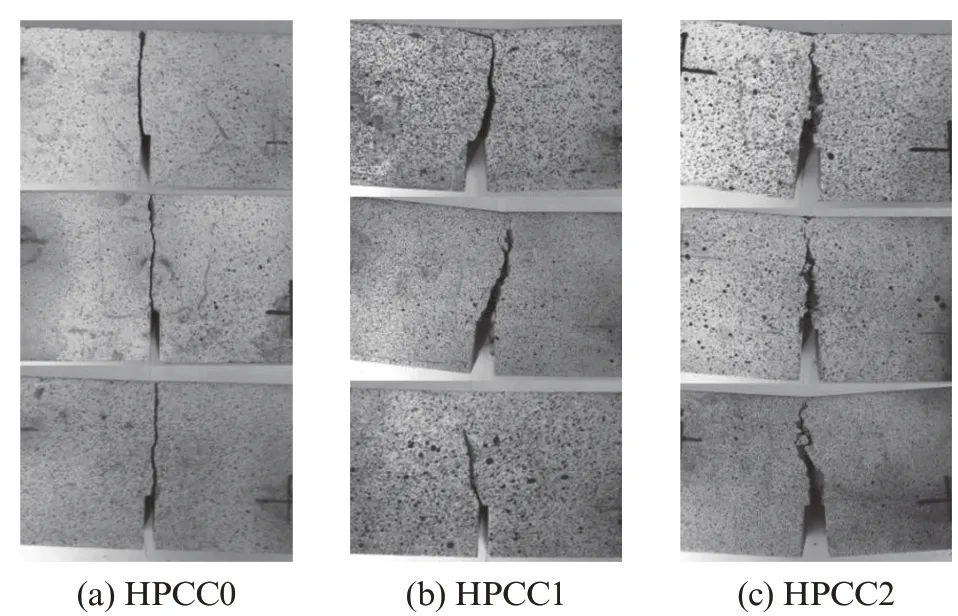
图2 HPCC试件的破坏形态Fig.2 Failure modes of HPCC specimens

2.2 F-CMOD曲线

HPCC试件的F-CMOD曲线见图3.从图3可以看出：加载初期不同钢纤维体积分数下试件的F-CMOD曲线基本重合；但是在峰值荷载前后曲线形态大有不同，不掺钢纤维试件HPCC0的加载曲线峰前部分几乎呈线性，峰后段荷载随着CMOD的增大迅速减小，表现出典型的脆性特征；而掺钢纤维试件的峰前存在明显的挠曲硬化行为，峰后段荷载随CMOD增大逐渐减小，展现了突出的韧性.

图3 HPCC试件的F-CMOD曲线Fig.3 F-CMOD curves of HPCC specimens

由图3还可以看出，随着钢纤维体积分数的增加，峰值荷载相应增大.带预制裂缝HPCC梁的三点弯曲强度f由下式得出［11］：

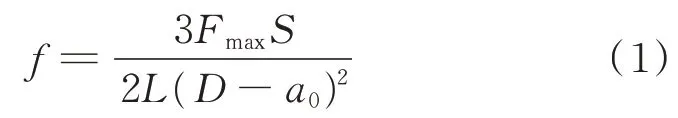
式中：Fmax为峰值荷载；S为跨度；D、L分别为试件的高度和宽度；a0为预制裂缝深度.

图4展示了HPCC试件弯曲强度与钢纤维体积分数的关系.由图4可见：HPCC试件弯曲强度随钢纤维体积分数增加呈近似线性增长，这是因为当微裂纹形成后，钢纤维对裂纹两侧基体起到了桥接作用，并且随着钢纤维体积分数的增加，钢纤维与基体之间的应力减小，从而延缓了裂纹的形成与扩展，弯曲强度随之提高.与不掺钢纤维试件相比，试件HPCC1和HPCC2的弯曲强度增幅分别为62%、145%.

图4 HPCC试件弯曲强度与钢纤维体积分数的关系Fig.4 Relationship between bending strength and steel fiber content of HPCC specimens

除了更高的弯曲强度，掺钢纤维试件较不掺钢纤维试件还具有出色的延性，这在F-CMOD曲线上表现为多峰和宽峰.由图3可见，HPCC试件虽然宽峰现象很显著，但是多峰现象并不显著，仅在HPCC2-S1中表现明显.对此，文献［12］指出，当纤维掺量低于临界纤维掺量时，复合材料不存在应变硬化和多重裂纹.

2.3 残余强度

为进一步了解钢纤维对试件F-CMOD曲线峰后行为的贡献，采用EN 14651（2007）《Test method for metallic fibre concrete-measuring the flexural tensile strength（limit of proportionality（LOP），residual）》和Fib Model Code 2010《Principles，models and test validation》推荐的方法对试件残余强度fR，i进行了评价.当CMOD值为0.5、1.5、2.5、3.5 mm时，分别计算残余强度fR，1、fR，2、fR，3和fR，4，fR，i计算公式为：

式中：FR，i为CMOD值为0.5、1.5、2.5、3.5 mm时对应的荷载.

不含钢纤维试件由于峰后软化迅速，无法根据推荐方法对残余强度进行分析.

表2列出了试件HPCC1、HPCC2的残余强度.由表2可见：与试件HPCC1相比，试件HPCC2的残余强度fR，1、fR，2、fR，3和fR，4均有所提高，增幅都在27%以上，说明较高的钢纤维体积分数会显著提高HPCC残余强度；但值得注意的是，随着fR，1变化到fR，4，残余强度的增幅从56.5%逐渐衰减到27.3%.残余强度增幅的逐渐减小说明钢纤维体积分数为2%的试件峰后荷载衰减更快，其峰后延展性更差，通过对比图3中峰后软化段的斜率也能直观看出这点.文献［13］对4种钢纤维体积分数（1%、2%、3%、4%）下超高性能钢纤维增强混凝土的弯曲行为进行了研究，同样发现微直钢纤维体积分数越高，软化区峰值载荷越大，峰后延展性越低.需要指出的是该现象并不适用于所有类型的钢纤维，文献［14］中采用端勾型钢纤维混凝土进行三点弯曲试验，其峰后延展性的表现就截然相反.

表2 试件HPCC1、HPCC2的残余强度Table 2 Residual strength of specimen HPCC1 and HPCC2

2.4 断裂特征参数

2.4.1 起裂韧度和失稳韧度

大量试验结果表明混凝土材料的断裂破坏特征呈准脆性，即混凝土裂缝的发展经历起裂、稳定扩展和失稳扩展3个过程.在混凝土裂缝扩展过程中，裂缝前端会萌生微裂纹并形成断裂过程区，且断裂过程区的发展造成混凝土F-CMOD曲线呈现非线性特征.考虑断裂过程区对钢纤维混凝土断裂韧性的影响，基于Xu等［15］提出的双K断裂准则，采用DL/T 5332—2005《水工混凝土断裂试验规程》推荐的计算公式，计算HPCC试件的起裂韧度KQΙC和失稳韧度KΙSC，结果见图5.由图5可见：HPCC起裂韧度KΙQC几乎不受钢纤维体积分数的影响，变化范围在0.62～0.68 MPa·m1/2之间，这是因为在基体开裂之前的线弹性承载阶段，基体间的黏聚力发挥主要作用，而钢纤维的锚固和黏结作用尚未被激活；与不掺钢纤维试件相比，掺钢纤维试件的失稳韧度KSΙC有很大提高，增幅达8倍以上，失稳韧度的提高可能是由于钢纤维发生了脱黏，相对于基体产生滑动，并通过在裂纹表面施加闭合牵引力而使基体裂纹稳定扩展；试件HPCC1、HPCC2的失稳韧度大致处于同一水平.Ren等［16］对6种微直钢纤维体积分数（0%～2.5%）下的混凝土梁进行了三点弯曲试验，得到的失稳韧度一同列于图5中.结合Ren等［16］的试验结果，可以认为钢纤维体积分数对HPCC失稳韧度提升具有一定的限值，在1%左右，当钢纤维体积分数继续增加时，其对失稳韧度的提升效果不明显.

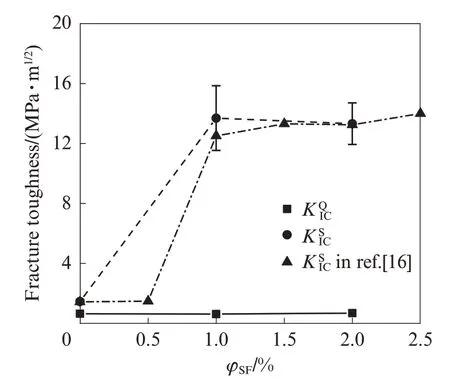
图5 HPCC试件的起裂韧度和失稳韧度Fig.5 Initial fracture toughness and unstable fracture toughness of HPCC specimens

2.4.2 断裂能

断裂能定义为产生单位断裂表面积所需的能量，通常被认为是一种材料特性.本文基于F-CMOD曲线来计算断裂能GF，采用的公式由JCI-S-001—2003《Method of test for fracture energy of concrete by use of notched beam》提供：

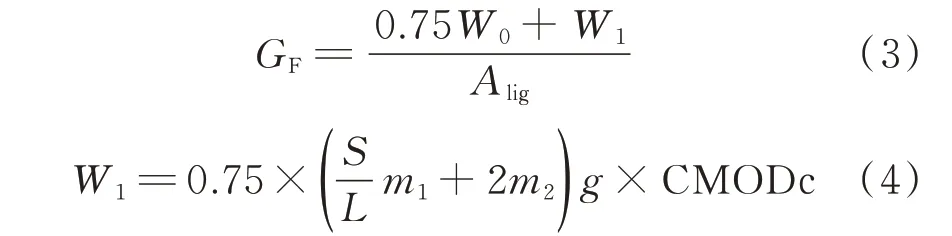
式中：W0为F-CMOD曲线下的面积；W1为试件自重和加载夹具所做的功；Alig为试件断裂面的面积；m1为试件的质量；m2为未附着在液压夹具上的弯曲压头质量；g为重力加速度；CMODc为试件破坏时的裂缝嘴张开位移.

需要说明的是，试验过程中含钢纤维的试件不会出现贯穿至梁顶的完全断裂现象，并且夹式引伸计量程有限，因此取CMODc＝4 mm用于断裂能的计算.HPCC试件断裂能与钢纤维体积分数的关系如图6所示.由图6可见，HPCC试件断裂能随着钢纤维体积分数的增加而增加，试件HPCC2的断裂能较试件HPCC1提高40%，而不掺钢纤维试件的断裂能（0.08 N/mm）和Fib Model Code 2010提出的C100普通混凝土断裂能（0.17 N/mm）都远远小于掺钢纤维试件.需要指出的是，若试验条件允许负荷持续降为0，则钢纤维混凝土梁的断裂能会进一步增加.

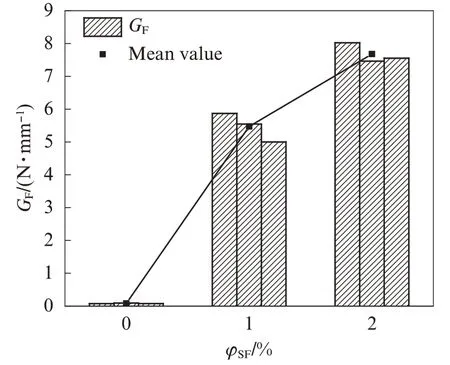
图6 HPCC试件断裂能与钢纤维体积分数的关系Fig.6 Relationship between fracture energy and steel fiber content of HPCC specimens

2.4.3 脆性指数

通常认为脆性是材料在发生重大不可逆变形之前突然断裂的倾向，Hillerborg等［17］综合考虑材料和结构尺寸的影响，提出了脆性指数B的计算公式：

式中：lch为特征长度；E为弹性模量；ft为极限拉伸强度，由狗骨头形状的试件经轴拉试验测得.

表3给出了HPCC试件的脆性指数。脆性指数越高，材料脆性越高.由表3可见：掺钢纤维能有效降低HPCC的脆性；但进一步比较钢纤维体积分数为1%和2%的HPCC试件，发现较高钢纤维体积分数对HPCC脆性的降幅很微小.

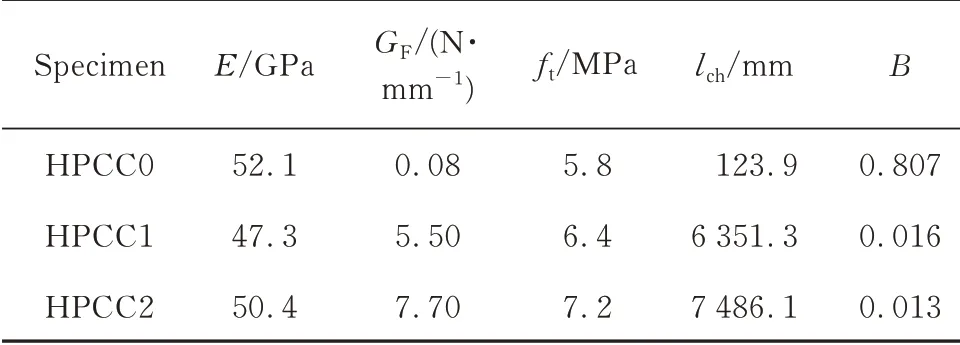
表3 HPCC试件的脆性指数Table 3 Brittleness of HPCC specimens

2.5 断裂面微观形态

图7给出了HPCC试件断裂面微观形态.图7（a）为HPCC基体SEM图，可以清楚地观察到区域A是充分水化后形成的致密层，而区域B结构较疏松，属于典型的尚未完全水化的基质.1条微裂纹在区域A、B的交界面形成，并由此诱发了周边多条细小的裂纹.图7（b）是基质致密层与疏松层交界面SEM图，可以看到裂纹沿着薄弱面扩展的迹象.加载初期微裂纹的形成与扩展主要由基体本身的性能决定，因此HPCC起裂韧度不受钢纤维体积分数的影响.图7（c）显示了钢纤维与基体的脱黏过程，这个过程中钢纤维的桥接作用被激活，钢纤维与基体间发生的相对滑移不仅迫使部分附着在钢纤维表面的薄弱基质被携带出来，而且钢纤维周围包裹的基质也会产生大量裂纹，从而引起F-CMOD曲线表现出典型的挠曲硬化特征.图7（d）显示了钢纤维与基体的剥离，此时钢纤维由于桥接应力的增大被明显拉长，大量的能量被消耗，HPCC断裂能因此大幅提升.同时泊松效应引起钢纤维横向收缩导致其与基体进一步脱黏，直至发生剥离，此时钢纤维与基体间依靠滑动摩擦来抵抗外荷载，黏聚力消失，对应F-CMOD曲线的软化区.图7（e）显示了钢纤维剥离后留下的滑动轨迹，可以看到残留的薄弱基质.值得一提的是，在SEM图中并没有观察到钢纤维断裂的现象，钢纤维失效的形式都是从基体中被拔出.

图7 HPCC试件断裂面微观形态Fig.7 Micro morphology of HPCC specimen fracture surface

3 结论

（1）HPCC弯曲强度随钢纤维体积分数增加呈近似线性增长，更高的钢纤维体积分数会明显提高HPCC的残余强度，F-CMOD曲线峰后延展性会随钢纤维体积分数增加而有所降低.

（2）HPCC起裂韧度几乎不受钢纤维体积分数的影响.掺钢纤维后其失稳韧度增幅可达8倍以上.钢纤维体积分数对失稳韧度的提升存在限值，约为1%.

（3）HPCC断裂能随着钢纤维体积分数的增加而增加，掺钢纤维能显著降低HPCC材料的脆性，但钢纤维体积分数进一步增加时，脆性的降幅很微小.

（4）HPCC加载初期微裂纹的形成与扩展主要由基体自身性能决定，钢纤维失效经历了纤维与基体脱黏和剥离的过程，失效模式为钢纤维拔出，钢纤维并未发生断裂.