条件概率的弱定义与随机事件间相依性的不同刻画
李兴东,杨 刚
(兰州交通大学 数理学院,兰州 730070)
随机事件之间及随机变量之间相依性及其度量,是概率统计中重要的研究课题之一.正如我国著名概率统计专家张尧庭教授所言,本文可引出许多随机变量之间相依性的指标,本文从不同的角度给出相依性的度量,并应尽快将这些内容吸收到统计教材中来[1-2].目前,文献[3-8]研究了Pearson相关系数、Kendall相依系数、Spearman秩相依系数等相依性度量指标的性质及其应用,这些相依性指标是随机变量间或随机向量间整体相依性的不同刻画及其度量.
因此,要准确地对复杂的相依性给出或微观或局部的度量,一条可行的途径就是首先探明随机事件间的相依性及其度量,然后将其方法与思路及其所得结论再拓展到随机变量间及随机向量间的相依性及其度量.条件概率是揭示随机事件之间及随机变量或随机变量序列之间相依性及其度量的基本工具[9],因条件概率正是从一随机事件的发生对另一事件发生的可能性的影响入手考虑相依性及其度量的.为能深入揭示相依性及其度量,必须对条件概率深入探讨.

事实上,概率为0的事件分为两类[11],概率为0的事件包含了不可能事件,不同于不可能事件,却常被误认为不可能事件.比如,在区间[0,1]上“取到有理数”的概率为0,但不是不可能事件.
本文中,首先将条件概率的定义进行推广,事件B可以是概率为0的事件,从而事件B为任意事件,A,B也就为任意两事件.为此,证明以下3个命题.
命题1设(Ω,F,P)是一个概率空间,对任意A,B∈F,则max{0,P(A)+P(B)-1}≤P(AB)≤min{P(A),P(B)}.
证明因A,B是概率空间(Ω,F,P)的任意两事件.一方面,因A∪B⊆Ω,由概率加法公式与单调性,有P(A∪B)=P(A)+P(B)-P(AB)≤P(Ω)=1,得P(AB)≥P(A)+P(B)-1;再由概率的非负性,得P(AB)≥0;故max{0,P(A)+P(B)-1}≤P(AB).
另一方面,因AB⊆A且AB⊆B,得P(AB)≤P(A)且P(AB)≤P(B),故P(AB)≤min{P(A),P(B)}.
从而,max{0,P(A)+P(B)-1}≤P(AB)≤min{P(A),P(B)}.
命题1给出了积事件概率不等式,由这个重要不等式,容易证明命题2与命题3也成立.
命题2在概率空间(Ω,F,P)中,若P(B)=0,则对任意事件A,有P(AB)=P(A)P(B),即0=P(A)×0.
命题3在概率空间(Ω,F,P)中,若P(B)=1,则对任意事件A,有P(AB)=P(A)P(B),即P(A)=P(A)×1.
由命题2与命题3,在同一个概率空间中,概率为0的事件、概率为1的事件都与任意事件独立,这与直观实际也是吻合的,即概率为0的事件和概率为1的事件都与任意事件独立,都不影响任意事件发生的概率.
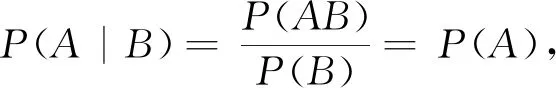
从而,给出条件概率的弱定义.文献[12]也给出了边缘密度函数为0的情形下二维随机变量的条件分布.
1 条件概率的弱定义
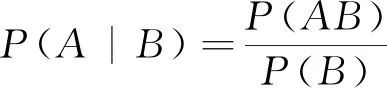
可见,弱定义中A,B是任意两事件,且允许分母P(B)=0.因此,以条件概率为基础的乘法公式、贝叶斯公式中都可以推广为任意事件,下文的事件都可以是任意事件.
接下来,基于积事件概率不等式的3个命题与条件概率的弱定义,进一步提出事件间的相依原理和相依度,从不同角度逐步深入、准确地刻画任意两随机事件之间的相依关系,也推广了条件概率、独立性等概念与相关概率命题的适用范围,使相关结论在具有更大理论价值和实践价值基础上,有更完美、对称的表达形式.
2 从不同角度刻画任意两随机事件之间的相依关系
基于条件概率的弱定义,能定性或定量地给出任意两随机事件相依性的不同刻画.
2.1 任意两随机事件相互独立的定性刻画
定性的,若同一个概率空间下的一事件的发生与否不影响另一事件发生的概率,则称两事件相互独立.在条件概率的弱定义下可以得到任意两事件相互独立的定量刻画或定义:设A,B是概率空间(Ω,F,P)的任意两事件,若P(AB)=P(A)P(B),则称A,B相互独立,简称A,B独立.否则,称A,B不独立或相依.这里,A与B都是允许概率为0或1的任意两事件.
1) 任意两随机事件的相依性是相互的
条件概率揭示了任意两随机事件的相依关系,且这任意两事件没有先后关系或因果关系,是成对出现的,其中的任何一个事件都可作为条件,这是对相依性的朴素认识.
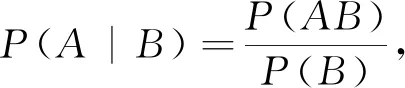
2) 由概率乘法公式刻画任意两随机事件之间的相依关系
设A,B是概率空间(Ω,F,P)的任意两事件,则P(AB)=P(A|B)P(B)=P(B|A)P(A).
3) 由贝叶斯公式刻画任意两随机事件之间的相依关系
贝叶斯公式的另一种表达形式是:
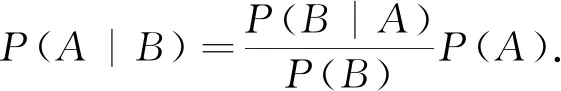
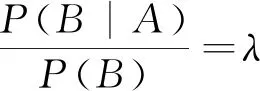
2.2 由似然度定量刻画任意两随机事件之间的相依关系
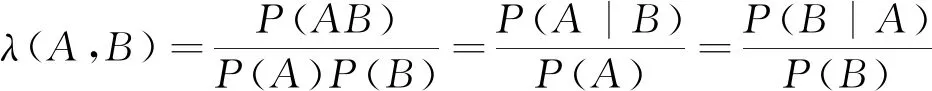
若λ(A,B)<1,则称A与B负相依;若λ(A,B)=1,则称A与B不相依(即独立);若λ(A,B)>1,则称A与B正相依;
可见,同一个概率空间的任意两事件A与B的似然度λ,实质是集合A与B的二元集函数,且函数值是非负实数.无论似然度λ取任何非负值,A与B彼此间的作用是相互的λ,似然度有如下性质.
性质1(任意两事件间的相依原理)设A,B是概率空间(Ω,F,P)的任意两事件,则有:
1)λ(A,B)=λ(B,A);
2) 任意两随机事件或负相依、或不相依、或正相依,三者必具其一且只具其一;
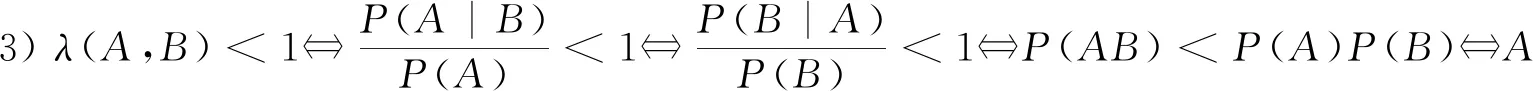

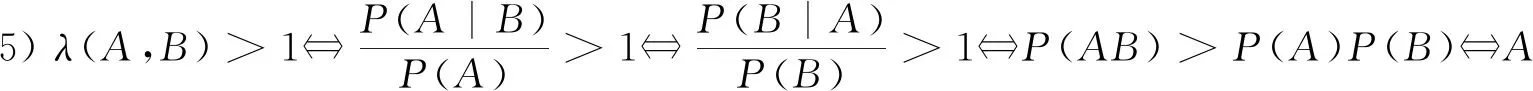
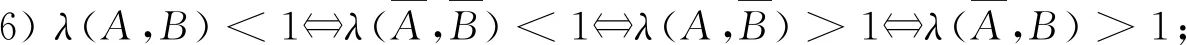
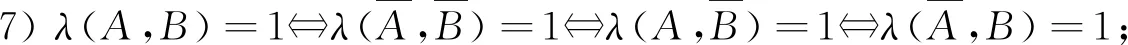

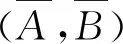
性质2设A,B是概率空间(Ω,F,P)的任意两事件,则有:

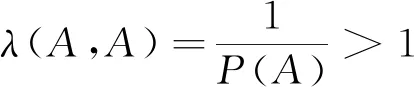
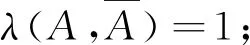
综上,同一个概率空间下任意两事件的似然度λ取非负实数值,定性并定量地刻画了A与B之间的相依关系:λ∈[0,1)时负相依;λ=1时独立;λ∈(1,+∞)时正相依.由性质2,似然度在区间[0,+∞)上以1为分界“非对称”地取值,主要定性地刻画了事件间的相依关系,但在定量方面,与下文提出的相依度相比有明显不足.
2.3 由相依度定量刻画任意两随机事件之间的相依关系
事实上,P(AB)-P(A)P(B)的符号(小于0、等于0、大于0)只是定性地反映了A与B是负相依、不相依还是正相依,只是一个绝对数,要相对地反映两事件相依程度的大小,需要知道P(AB)的最小值和最大值,由命题1,m=max{0,P(A)+P(B)-1}≤P(AB)≤min{P(A),P(B)}=M,因此,分别考虑积事件的概率到独立时的距离,积事件概率的最值到独立时的距离,两者之比能精确地刻画A与B相依程度的大小,即为A,B的相依度.文献[13]也给出了随机变量之间的相依度函数.
定义3设A,B是概率空间(Ω,F,P)的任意两事件,则称
ρ(A,B)=
为A,B的相依度.
由相依度的定义,若给定P(A),P(B),则对于在区间[m,M]中取值的P(AB),闭区间[-1,1]中存在唯一的相依度ρ(A,B)与之对应,反之亦然.从而,若给定P(A),P(B),则P(AB)与A,B的相依度ρ(A,B)之间存在一一映射关系.
当m≤P(AB) 当P(AB)=P(A)P(B)时,ρ(A,B)=0,称为不相依,即独立; 当P(A)P(B) 特别,当P(AB)=m时,ρ(A,B)=-1,称为完全负相依;当P(AB)=M时,ρ(A,B)=1,称为完全正相依. 显然,相依度也是集合A与B的二元集函数.可以验证,相依度有以下较好性质: 性质3设A,B是概率空间(Ω,F,P)的任意两事件,则有: 1) -1≤ρ(A,B)≤1; 2)ρ(A,B)=ρ(B,A); 4) |ρ|越小,相依程度越弱;|ρ|越大,相依程度越强;|ρ|=1,相依程度最大; -1. 以下实例,说明了两事件的似然度、相依度的具体求解,并验证了性质1、性质2与性质3. 例1在同一个概率空间下,已知P(A)=0.2,P(B)=0.3,并设P(AB)=0.15,分别解答: 1)λ(A,B),ρ(A,B);并说明A,B相依关系; 上文基于条件概率的弱定义,从多个角度定性并定量地逐步深入刻画了同一个概率空间的任意两事件的相依性及其度量,并已扩大了相关概率命题的应用范围,使相关结论在具有更大理论价值和实践价值基础上,有更完美、对称的表达形式.为进一步论证,下文再给出了任意两事件负相依、不相依、正相依的其他等价刻画,并结合一个具体实例,说明相关概率命题应用范围的扩大. 1) 任意两事件负相依的其他等价刻画 设A,B是概率空间(Ω,F,P)的任意两事件,A与B负相依等价于 2) 任意两事件不相依的其他等价刻画 设A,B是概率空间(Ω,F,P)的任意两事件,A与B不相依等价于 3) 任意两个事件正相依的其他等价刻画 设A,B是概率空间(Ω,F,P)的任意两事件,A与B正相依等价于 4) 相关概率命题应用范围的扩大 现行教材中,条件概率公式、乘法公式、全概率公式、贝叶斯公式中都要求分母大于0.在条件概率的弱定义下,其分母都可以等于0;本文中,其中的事件都是任意事件,既扩大了相关概率命题的应用范围,又使数学表达对称、统一. 本文从条件概率的概念出发,提出了条件概率的弱定义、事件间的相依原理和事件间的相依度,从不同角度逐步深入、准确地刻画了同一个概率空间的任意两随机事件之间的相依关系及其度量,并使建立在条件概率基础上的相关命题有形式与本质的统一. 正如我国著名概率统计专家张尧庭教授所言,本文可引出许多随机变量之间相依性的指标,从不同的角度给出相依性的度量,并应尽快将这些内容吸收到统计教材中来.笔者认为,基于条件概率的弱定义,以相依性为线索,也可以构建概率统计的主要内容、方法与原理,在理论方面与实践方面都具有“潜在”意义.本文从事件的角度作了基础性的有意义的探索. 基础性是显而易见的,有意义表现在:本文给出了两随机事件间相依性的不同刻画及其度量,特别是提出了两事件的相依度,能较准确地度量两事件相依程度.本文方法与思路及其所得结论可拓展到随机变量间及随机向量间的相依性及其度量,对应的就能得到随机变量间或随机向量间相依性的不同刻画及其度量,相应的相依度与Pearson相关系数、Kendall相依系数、Spearman秩相依系数等相依性度量指标有密切关系,能克服这些度量指标的不足,能适应各种相依类型,较准确地对复杂的相依性给出或微观或局部或整体的度量.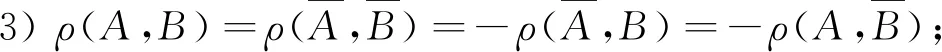

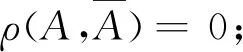
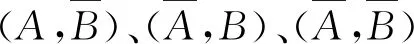


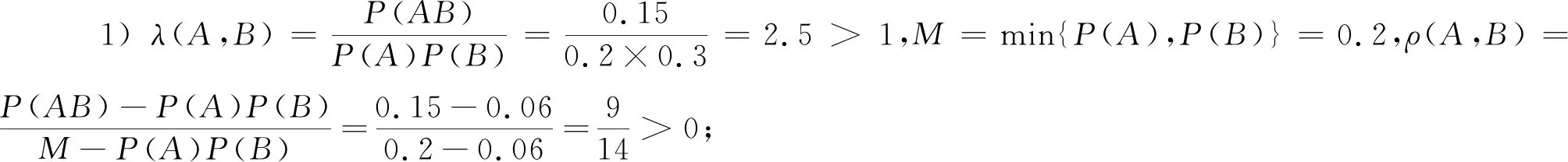
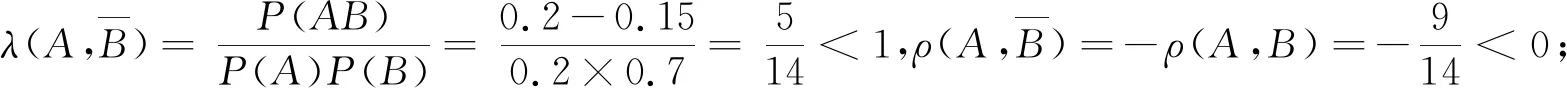
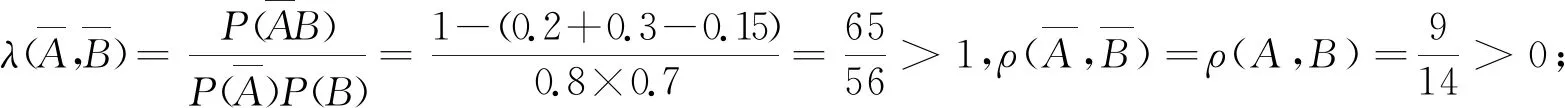
3 相依性的其他等价刻画与相关概率命题应用范围的扩大
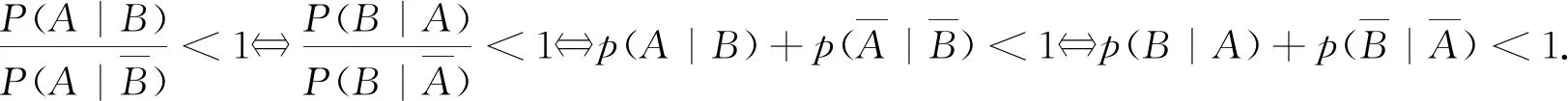
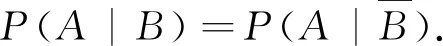
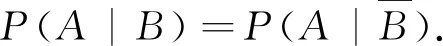

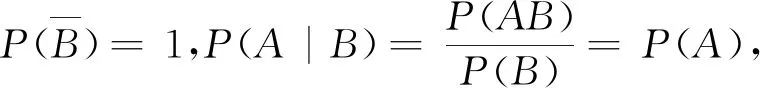
4 结束语

