利用优选状态数的MCMC模拟农机装备负载

杨子涵，宋正河

利用优选状态数的MCMC模拟农机装备负载

杨子涵，宋正河※

（中国农业大学现代农业装备优化设计北京市重点实验室，北京 100083）

传统马尔科夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）方法中状态数的选取常依赖于主观经验，用于农机装备负载模拟时，状态数取值不当将导致负载模拟精度降低或算法运行时间冗长。针对此问题，该研究提出一种基于伪损伤一致性的状态数优选方法。首先确定MCMC算法中状态数的初选范围，然后分别计算范围内不同状态数所对应的负载模拟结果，最后以生成的模拟负载与原始载荷之间的损伤一致性为评价准则确定优选状态数。利用拖拉机关键零部件的实测载荷数据对该方法进行验证。结果表明，随着状态数的提高，模拟负载与原始载荷之间的损伤一致性变化趋于平稳，算法运算时长增速不断提高，相比于传统方法，基于优选状态数的MCMC算法能够得到伪损伤差异在1%以内的负载模拟结果，与载荷谱编制的目标需求更加匹配，在保证模拟结果精度的同时有效减少运算成本。该研究能够为农机装备关键零部件的动态仿真分析及可靠性试验提供更加可靠的数据支撑。

农业机械；模拟；载荷；马尔科夫链；蒙特卡洛法；优选状态数；伪损伤

0 引 言

随着农业装备不断向现代化、智能化和规模化发展，农业装备生产企业愈发重视产品的可靠性问题[1-2]。如今，为了争夺更广阔的市场资源，企业必须以适应不同地域、不同作业需求为目标生产耐用可靠的机器[3]。为实现这一目标，研发人员需在产品投放市场前能够对产品整机及关键零部件的疲劳寿命做出更为精准的预估[4-5]。动力机械的载荷不稳定、随机波动和随时间变化等特征是对其可靠性产生威胁的重要因素[6]。因此，如何准确获取产品在实际作业工况下的载荷特征，编制全生命周期载荷谱成为了可靠性研究领域的一个重要课题[7]。相比于一般动力机械，农业装备的作业环境更加恶劣，工况复杂多变且具有明显的季节性作业特征，使农业装备载荷谱编制变得更加复杂。

针对飞机关键部件结构试验的载荷谱最先被提出，这种谱块形式的程序载荷谱主要以疲劳线性累计理论为支撑，对于台架动态加载性能要求较低，因此被广泛应用于车辆、船舶、风机等领域[8-9]。随着研究的深入，越来越多的文献表明，载荷的均值、加载的顺序和频率同样会对结构的疲劳失效产生不可忽略影响[10]。因此，更为细腻且考虑载荷加载顺序的载荷谱编制方法开始出现，如考虑变均值混合工况的车辆载荷谱CARLOS和海洋平台载荷谱Wash[11]。国内闫楚良等[12]根据飞机实际受载特征提出了高置信度中值随机疲劳载荷谱编制方法。随着电气和液压伺服系统的出现及有限元仿真技术的快速发展，如今，载荷谱的加载形式已不再局限于简化后的谱块形式[13]，在此背景下，如何基于短时的实测载荷信息模拟出能够满足试验台长期加载及全生命周期仿真需求的载荷时间序列，进一步缩减测试成本成为了新的研究热点。

目前已有的负载模拟方法主要有雨流域、时域、频域等。雨流域的相关研究[14-15]发展较早且技术最为成熟，但是由于无法保留负载的时序信息限制了其应用范围。从频域角度对负载进行建模能够反映出实测载荷样本的物理含义，目前应用对象主要集中于频谱特征明显的旋转部件[16-17]。近年来又有学者将机器学习的相关方法应用于载荷模拟[18]，由于对载荷样本要求较高并且需人工划分工况，因此未得到广泛应用。

以获取与实测信号时域特征相一致的载荷时间序列为目标的时域模拟技术是目前的主流研究方向。Johannesson[19]提出了基于极值理论载荷时域外推方法，随后众多学者针对该方法的关键技术进行了深入研究，然而该类方法仅对超出阈值的极端载荷进行建模，忽略了对一般载荷的模拟重构。MCMC（Markov chain Monte Carlo）方法能够基于负载变化特征更全面地模拟载荷时间序列。Rychlik等[20]提出了利用马尔科夫链对随机负载进行建模的方法，并利用实测卡车负载数据对该方法进行了验证。Carboni等[21]利用马尔科夫状态转移矩阵对液压泵负载进行建模，并利用负载累积时间曲线重构负载的持续时长，解决了马尔科夫域无法保留时域信息的问题。武玉倩[22]讨论了驾驶员行为特征对负载的影响，提出了基于隐马尔科夫模型的载荷谱外推方法。Cerrini等[23]针对混凝土灌装机械的铰接臂负载，提出了一种改进的马尔科夫建模方法，能够考虑状态切换所造成的负载差异。Wang等[24]基于MCMC方法提出了应用于装载机非平稳负载的循环工况模拟方法。刘纯等[25]将MCMC方法应用于风电出力时间序列的模拟。在农机装备领域，Paraforos等[26-27]利用马尔科夫链对搂草机械机体应变载荷和拖拉机油耗进行建模，通过蒙特卡洛方法生成了时频特征较为一致的模拟结果。

需要注意的是，上述MCMC方法中马尔科夫链的状态数选取均依赖于主观经验，如文献[24]中所描述的状态数取值一般为32或64，文献[27]中选取的状态数则为256。徐沈智等[28]以模拟序列与原始序列的自相关特性为评判准则，讨论了风电功率序列建模时状态数对于模拟结果的影响，并提出了基于ACF（Auto-Correlation Function）曲线距离最小的状态数选取方法。然而风电功率序列与农机装备负载在数据特征与应用方式上有着本质差异，因此并不适用农机装备负载模拟。

基于此，本文首先讨论了MCMC方法应用于农机装备负载模拟时，状态数取值对于模拟结果的影响。在此基础上，以保障载荷谱编制精度为目标，提出了一种基于伪损伤一致性的状态数优选方法。最后以拖拉机犁耕工况下前桥振动负载为例验证了状态数选取的合理性，进一步讨论了农机装备不同作业段负载差异对于状态数选取结果的影响，并给出了基于优选状态数的MCMC算法在农机装备负载模拟中的应用范例。

1 基于优选状态数的MCMC方法

1.1 MCMC方法

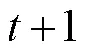
需要注意的是，与传统马尔科夫链应用方式不同，在对实测载荷序列进行建模时，往往只关注与局部极端载荷，即实测载荷序列中局部最大值与最小值所组成的转折点序列，这种方式能够在保留载荷时域信息的同时有效缩减数据量。利用MCMC方法对实测载荷进行模拟的具体步骤如下：

1）载荷时域特征提取。首先对实测载荷信号进行峰谷值提取，得到转折点序列{X}，然后将峰值序列{1,2,…}与谷值序列{1,2,…}分别进行提取，并记录升程S对应的时间间隔ΔT和降程s对应的时间间隔Δt：

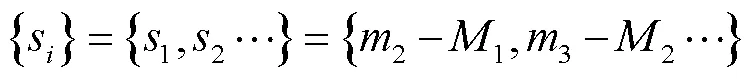
为便于蒙特卡洛模拟，进一步计算上述概率矩阵的累计概率矩阵：

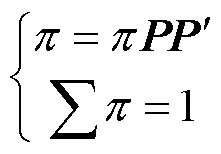
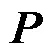
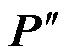
1.2 状态数选取对载荷模拟结果的影响

本文选取拖拉机犁耕作业和整地作业工况下关键零部件的振动、应力和扭矩负载作为验证数据集，如图1所示。

犁耕工况下前桥的振动和应力载荷数据采集于北京上庄试验站，拖拉机型号为约翰迪尔6B-1354，挂接机具为1LF-535型液压翻转犁，犁耕作业时拖拉机档位为B2挡，作业速度为5～10 km/h，作业路径如图2a所示。整地工况下的传动轴扭矩载荷数据采集于江苏盐城新洋试验站，拖拉机型号为东方红LX2204，挂接机具为HR4004D型驱动靶，整地作业时拖拉机档位为中三档，作业速度为2～6 km/h，作业路径如图2b所示。

上述两种工况下的田间试验均于当地春耕作业季内开展，试验严格参照标准T/NJ 1252—2020《拖拉机田间作业机组试验规程犁耕作业》和T/NJ 1253—2020《拖拉机田间作业机组试验规程整地作业》进行，试验用传感器及设备信息如表1所示。选用当地经验丰富的机手驾驶拖拉机，试验过程中不存在对于机手作业方式的干预，采集的载荷数据能够有效代表当地实际的农业生产作业特点。

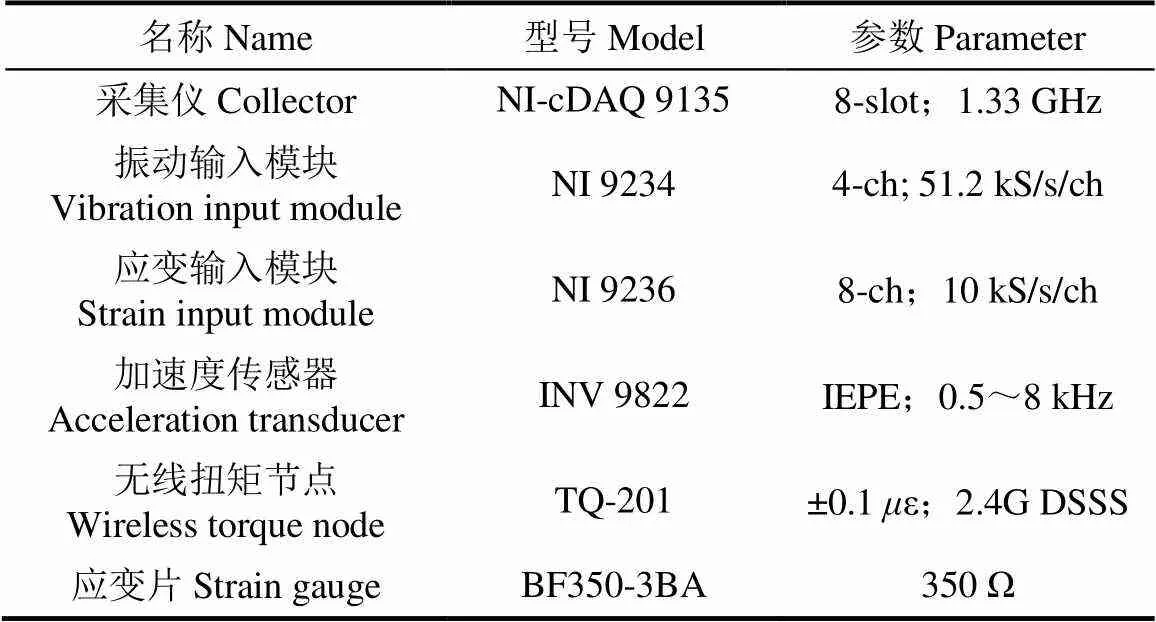
表1 传感器及设备信息

由图1和图2可知，田间作业时随着拖拉机行驶状态的循环切换，作业机具与拖拉机之间、作业机具与土壤之间的力和位置关系发生改变，拖拉机关键零部件所承受的负载特征也同步产生变化。以犁耕工况为例，根据拖拉机行驶状态，可以将该工况细分为作业阶段和调整阶段，两个阶段交替切换构成目标地块的一次完整作业，如图3a所示。

图3b中根据拖拉机行驶状态不同将实测载荷划分为16个载荷片段，可以看出，拖拉机犁耕工况负载在作业阶段（O1～O8）和调整阶段（A1～A8）具有明显的特征差异。作业阶段拖拉机牵引负荷较大，当犁具调整完毕后耕作深度保持相对稳定，因此振动量级偏大但是各负载之间差异较小。调整阶段机具处于提升状态，牵引阻力较小，振动主要由路面激励引起，相对于作业阶段载荷量级较小，但是由于田间路面及车速差异明显，波动较为剧烈且负载之间差异明显。

MCMC方法在处理由特征差异明显的片段所组成的载荷时间序列时，会破坏原有特征片段的独立性。简单的解决方式即分别提取原始负载中各个特征片段分别进行模拟，再通过循环仿真的方式实现负载重构[24]。因此，本文首先以拖拉机犁耕工况下前桥桥臂所受的振动载荷为研究对象，截取单次作业片段的载荷数据进行分析，讨论状态数选取对载荷模拟结果的影响。

可靠性常用雨流计数法得到的雨流矩阵来统计载荷循环的特征信息，因此可用雨流矩阵间的相似程度来间接评价模拟结果与实测载荷的一致性。雨流差值矩阵的-范数（Frobenius norm）可由下式得出：

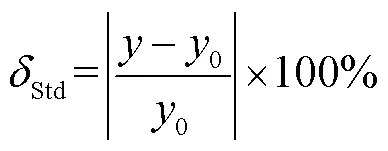
由图4a可知，随着状态数增加，MCMC方法模拟结果的均值相对误差和标准差相对误差会迅速降低并趋于稳定，相比于均值相对误差，标准差相对误差会更快趋于稳定。与宏观的统计特征不同，-范数能够从载荷循环均幅值所构成的二维空间对模拟结果进行相似性评价，评价结果也更为细致。由图4b可知，随状态数增加，-范数逐渐降低，虽然数值下降的速度逐渐平缓但具有持续下降的趋势。

综上可以看出，状态数的增加会提高MCMC方法负载模拟的精度，但是上述特征评价指标均不能给出客观一致且具有实际理论意义的状态数选取方案。基于此，本文提出一种基于伪损伤一致性的状态数优选方法。

1.3 基于伪损伤一致性的状态数选取方法

针对农机装备关键零部件实测载荷进行模拟的目的是指导产品的可靠性设计，因此本文尝试从损伤角度入手指导MCMC方法应用于负载模拟时状态数的选取。构建农机装备关键零部件载荷谱所需要考虑的载荷种类不仅仅局限于应变或应力载荷，还包括扭矩、压力、振动、牵引力等。此外，大多数农机装备关键零部件并不具备精准的疲劳应力循环曲线（S-N曲线）信息，精准的疲劳寿命预测往往需要大量的试验，耗时费力。

伪损伤理论能够在一定程度上反映外部激励载荷对结构件造成损伤的潜在能力已被证实[29]。通过计算伪损伤，能够在零部件S-N曲线未知的情况下，实现不同载荷片段之间损伤程度的定量评价。因此，本文引入伪损伤理论，通过计算载荷模拟前后的伪损伤值实现状态数的定量选取。基于伪损伤一致性的状态数选取方法过程如下：

1）利用雨流计数法提取实测载荷中每个负载循环信息，基于修正的Miner准则，将所有载荷循环的损伤值进行累加：

式中为总累计损伤；1/δ为实测第个载荷循环所造成的损伤值；为载荷循环次数；为结构材料S-N曲线的反斜率系数；S为第个载荷循环幅值；为常数变量。

2）由于伪损伤与结构材料参数并无严格对应关系，因此伪损伤简化为

LDH检测：空腹采集患者静脉血，不抗凝，离心分离血清。应用LDH检测试剂盒（成都元和华盛股份有限公司产品）和i2000全自动生化分析仪（美国Abbott Laboratories公司产品）检测LDH。正常值参考范围：150～245 U/L。

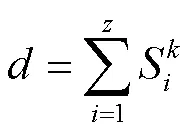
由公式（12）可知，伪损伤仅与载荷循环幅值和反映材料疲劳特性的反斜率系数有关。借鉴汽车零部件的伪损伤计算准则，对于焊接结构件或发生裂纹扩展的零部件，取3；对于典型的表面粗糙零部件，取5；对于具有光滑表面的零部件，取7[29]。

3）分别计算不同状态数下模拟负载产生的伪损伤，进一步利用公式（13）计算不同状态数对应的伪损伤系数。越接近于1，模拟负载与原始负载的伪损伤一致性越高。

式中0为原始负载对应的伪损伤。

设定伪损伤系数的上限阈值为Q，选取低于阈值且数值最小的状态数作为优选状态数。综上，利用优选状态数的MCMC方法流程如图5所示。

2 结果与分析

为验证本文状态数选取方法的有效性，选取1.2节中截取的单程犁耕作业片段进行实例分析。首先，依次计算不同状态数取值所对应的原始载荷等长度模拟结果的伪损伤系数。本文状态数的初选范围为[4,300]，由于负载模拟过程具有一定随机性，每次模拟结果的伪损伤系数并不完全一致。为消除随机性对于负载模拟结果的影响，针对每个状态数取值分别进行100次独立重复试验，计算结果取平均值作为该状态数对应伪损伤系数的最终结果。状态数与伪损伤系数的对应关系及算法用时如图6所示。

由图6可知，与原始载荷相比，MCMC方法得到的载荷模拟结果的伪损伤系数整体偏大，随着状态数增加，模拟结果的伪损伤系数会迅速降低后趋近与1，而算法的运算时长保持有上升的趋势且增速不断提高。为在满足模拟精度的前提下尽可能缩减运算成本，本文将伪损伤系数的阈值设定为1.01，即与原始载荷伪损伤的差异在1%以内，得出该负载片段的优选状态数为34。

将原始载荷与模拟结果分别进行雨流计数并绘制载荷循环幅值累计频次曲线，如图7所示。可以看出，状态数取值过低时，模拟负载的循环幅值偏大，致使生成的载荷谱更为恶劣，在状态数达到优选状态数后，比优选状态数更大的取值对提高载荷模拟精度的作用变得十分有限，这和伪损伤系数与状态数的变化关系相一致，验证了本文状态数选取方法的有效性。

按照本文方法对1.2节各载荷片段（O1～O8，A1～A8）依次进行分析，计算出各片段的优选状态数及相应的伪损伤系数，如表2所示。由表2可知，基于伪损伤一致性的状态数选取方法可以有效适用于犁耕工况下各振动载荷片段，基于优选状态数的负载模拟结果均能够满足设定的伪损伤一致性要求。此外，受农机装备田间作业特点影响，即使在单一犁耕工况下，由于载荷特征不一致，不同载荷片段对应的优选状态数计算结果同样具有差异性。相比于作业阶段，调整阶段各载荷片段之间的差异更为明显，优选状态数计算结果也更加分散。因此，在利用MCMC方法对农机装备作业载荷进行模拟时有必要针对不同负载片段分别进行优选状态数的确定。

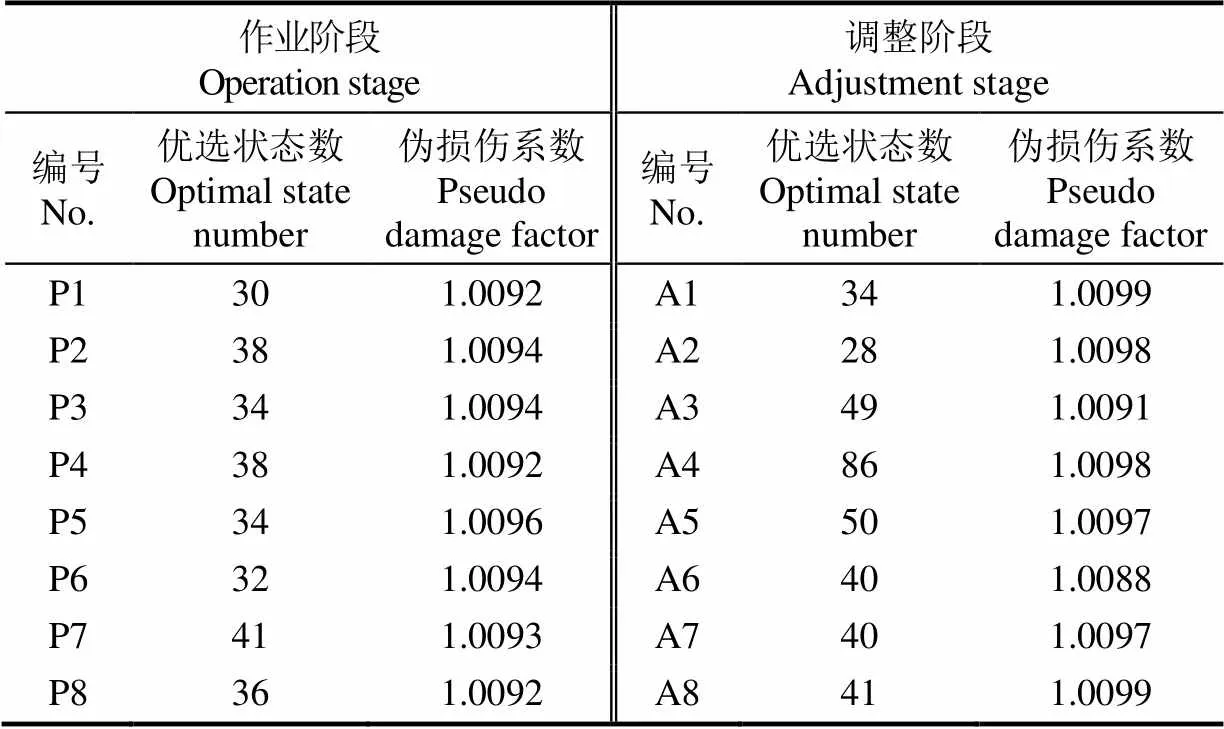
表2 犁耕工况下各载荷片段的优选状态数

同理，对1.2节中犁耕工况下前桥应力负载和整地工况下传动轴扭矩负载分别进行循环模拟。为进一步验证所述方法对于拖拉机各关键零部件在不同作业工况下所受负载的适用性，提取循环模拟结果中各载荷片段的均值、标准差和载荷循环幅值最大值作为统计特征值，按照负载类型不同进行划分，将各载荷片段模拟结果特征值与原始载荷相应特征值的差值作为一个集合，得到各统计特征值的偏差范围[min,max]如表3所示，min和max分别为差值集合中的最小值和最大值。

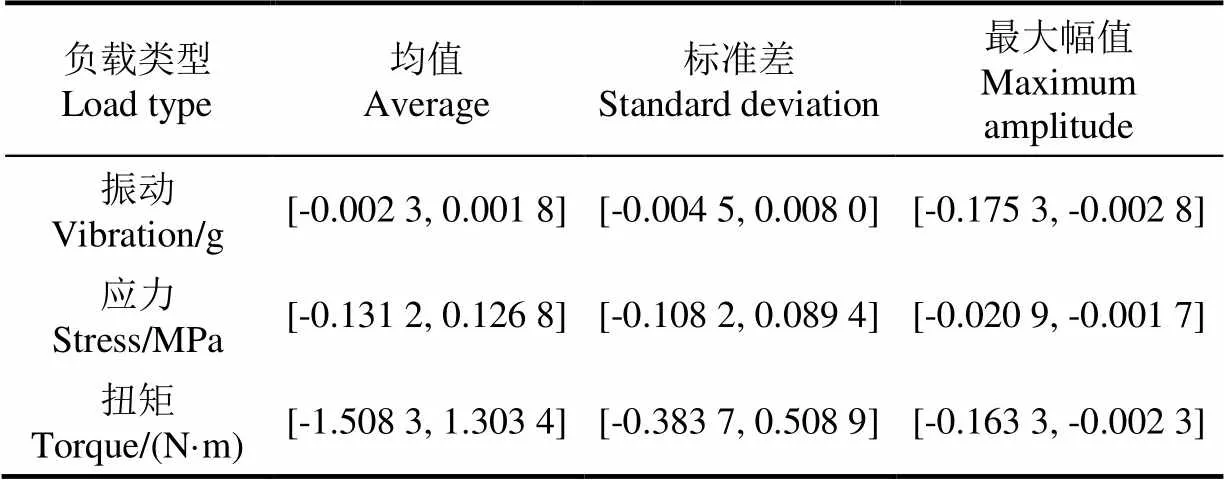
表3 各载荷片段模拟结果的统计特征值偏差范围

作为一种基于统计学原理的建模方式，理论上本文方法对于不同工况下不同类型和特征的负载数据具有通用性。由表3各统计特征值的对比结果可知，各负载片段的模拟结果与原始负载间的特征值差值范围很小，进一步验证了本文方法用于以载荷谱编制为目标的农机装备负载模拟的通用性。

3 结 论

针对传统MCMC方法中状态数选取缺乏理论依据的问题，以拖拉机前转向驱动桥犁耕作业时所受到的振动载荷为对象，研究不同状态数取值对于负载模拟精度的影响并提出状态数优选方法。主要结论如下：

1）状态数取值不同会对负载模拟结果精度产生重要影响。随着状态数取值的增加，模拟负载与原始载荷之间的均值误差、标准差误差和雨流矩阵偏差会快速减小并趋于稳定。

2）提出了基于伪损伤一致性的状态数选取方法。随着状态数提高，模拟负载与原始载荷之间的损伤一致性逐渐提高并趋于平稳，而算法运算时长的增速依然不断提高。通过设定伪损伤系数的阈值，即可计算出满足损伤一致性要求且运算时长最小的优选状态数。

3）实例分析结果表明，基于优选状态数的MCMC方法能够得到伪损伤差异在1%以内的载荷模拟结果，各负载片段的模拟结果特征值与原始载荷特征值具有较高的一致性。与传统方法相比，基于优选状态数的MCMC方法与载荷谱编制的目标更加匹配，能够满足拖拉机各关键零部件在不同工况下的负载模拟需求，在保证负载模拟精度的前提下有效减少了运算成本。

[1] 谢斌，武仲斌，毛恩荣. 农业拖拉机关键技术发展现状与展望[J]. 农业机械学报，2018，49(8)：1-17.

Xie Bin, Wu Zhongbin, Mao Enrong. Development and prospect of key technologies on agriculture tractor[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 51(8): 131-136. (in Chinese with English abstract)

[2] 尹宜勇，付宁善，廖频，等. 基于DTW距离的拖拉机传动轴载荷样本长度计算方法[J]. 农业工程学报，2020，36(12)：54-60.

Yin Yiyong, Fu Ningshan, Liao Pin, et al. Calculation method of load sample size for tractor drive shafts based on dynamic time warping distance[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(12): 54-60. (in Chinese with English abstract)

[3] Paraforos D S, Griepentrog H W, Vougioukas S G. Modeling and simulation of a four-rotor rake loading for predicting accumulated fatigue damage: A Markov regime-switching approach[J]. Applied Engineering in Agriculture, 2018, 34(2): 317-325.

[4] Wen C K, Xie B, Song Z H, et al. Methodology for designing tractor accelerated structure tests for an indoor drum-type test bench[J]. Biosystems Engineering, 2021, 205: 1-26.

[5] 杨子涵，宋正河，尹宜勇，等. 基于POT模型的大功率拖拉机传动轴载荷时域外推方法[J]. 农业工程学报，2019，35(15)：40-47.

Yang Z, Song Z, Yin Y, et al. Time domain extrapolation method for load of drive shaft of high-power tractor based on POT model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(15): 40-47. (in Chinese with English abstract)

[6] 轩福贞，朱明亮，王国彪. 结构疲劳百年研究的回顾与展望[J]. 机械工程学报，2021，57(6)：26-51.

Xuan Fuzhen, Zhu Mingliang, Wang Guobiao. Retrospect and prospect on century-long research of structural fatigue[J]. Journal of Mechanical Engineering, 2021, 57(6): 26-51. (in Chinese with English abstract)

[7] 陈道云，孙守光，李强. 高速列车载荷谱推断及扩展方法研究[J]. 机械工程学报，2018，54(10)：151-155.

Chen Daoyun, Sun Shouguang, Li Qiang. Study on deduction and extend of high-speed train load spectrum[J]. Journal of Mechanical Engineering, 2018, 54(10): 151-155. (in Chinese with English abstract)

[8] 高云凯，徐成民，方剑光. 车身台架疲劳试验程序载荷谱研究[J]. 机械工程学报，2014，50(4)：92-98.

Gao Yunkai, Xu Chengmin, Fang Jianguang. Study on the programed load spectrum of the body fatigue bench test[J]. Journal of Mechanical Engineering, 2014, 50(4): 92-98. (in Chinese with English abstract)

[9] 张英爽，王国强，王继新，等. 工程车辆传动系载荷谱编制方法[J]. 农业工程学报，2011，27(4)：179-183.

Zhang Yingshuang, Wang Guoqiang, Wang Jixin, et al. Compilation method of power train load spectrum of engineering vehicle[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(4): 179-183. (in Chinese with English abstract)

[10] Branigan Z, Suh C S. Power density-an alternative approach to quantifying fatigue failure[J]. Journal of Vibration Testing and System Dynamics, 2018, 2(4): 307-326.

[11] Heuler P, Klätschke H. Generation and use of standardised load spectra and load-time histories[J]. International Journal of Fatigue, 2005, 27(8): 974-990.

[12] 阎楚良，高镇同. 飞机高置信度中值随机疲劳载荷谱的编制原理[J]. 航空学报，2000(2)：118-123.

Yan Chuliang, Gao Zhentong. Compilation theory of median stochastic fatigue load spectrum with high confidence level for airplane[J]. Acta Aeronautica et Astronautica Sinica, 2000(2): 118-123. (in Chinese with English abstract)

[13] Sonsino C M. Fatigue testing under variable amplitude loading[J]. International Journal of Fatigue, 2007, 29(6): 1080-1089.

[14] Nagode M, Klemenc J, Fajdiga M. Parametric modelling and scatter prediction of rainflow matrices[J]. International Journal of Fatigue, 2001, 23(6): 525-532.

[15] Johannesson P, Thomas J J. Extrapolation of rainflow matrices[J]. Extremes, 2001, 4(3): 241-262.

[16] Poirier M, Gagnon M, Tahan A, et al. Extrapolation of dynamic load behaviour on hydroelectric turbine blades with cyclostationary modelling[J]. Mechanical Systems and Signal Processing, 2017, 82: 193-205.

[17] Wen Y K, Gu P. Description and simulation of nonstationary processes based on Hilbert spectra[J]. Journal of Engineering Mechanics, 2004, 130(8): 942-951.

[18] Qin C, Shi G, Tao J, et al. Precise cutterhead torque prediction for shield tunneling machines using a novel hybrid deep neural network[J]. Mechanical Systems and Signal Processing, 2021, 151: 107386.

[19] Johannesson P. Extrapolation of load histories and spectra[J]. Fatigue & Fracture of Engineering Materials & Structures, 2006, 29(3): 209-217.

[20] Rychlik I. Simulation of load sequences from rainflow matrices: Markov method[J]. International Journal of Fatigue, 1996, 18(7): 429-438.

[21] Carboni M, Cerrini A, Johannesson P, et al. Load spectra analysis and reconstruction for hydraulic pump components[J]. Fatigue & Fracture of Engineering Materials & Structures, 2008, 31(3‐4): 251-261.

[22] 武玉倩. 基于隐马尔科夫模型的装载机载荷谱编制方法研究[D]. 长春：吉林大学，2017.

Wu Yuqian. Research on Load Spectra Compilation Method of Loaders Based on Hidden Markov Model[D]. Changchun: Jilin University, 2019. (in Chinese with English abstract)

[23] Cerrini A, Johannesson P, Beretta S. Superposition of manoeuvres and load spectra extrapolation[C]. Applied Mechanics and Materials, Trans Tech Publications Ltd, 2006, 5: 255-262.

[24] Wang J, Zhang J, Liang Y, et al. A cyclic simulation approach for the generation of the non-stationary load histories of engineering vehicles[J]. Journal of Mechanical Science and Technology, 2012, 26(5): 1547-1554.

[25] 刘纯，吕振华，黄越辉，等. 长时间尺度风电出力时间序列建模新方法研究[J]. 电力系统保护与控制，2013，41(1)：7-13.

Liu Chun, Lü Zhenhua, Huang Yuehui, et al. A new method to simulate wind power time series of large time scale[J]. Power System Protection and Control, 2013, 41(1): 7-13. (in Chinese with English abstract)

[26] Paraforos D S, Griepentrog H W. Switching Markov chains for modelling the loads of a four-rotor swather under different operating modes[J]. IFAC-PapersOnLine, 2017, 50(1): 5392-5397.

[27] Paraforos D S, Griepentrog H W. Tractor fuel rate modeling and simulation using switching Markov chains on CAN-Bus data[J]. IFAC-PapersOnLine, 2019, 52(30): 379-384.

[28] 徐沈智，艾小猛，邹佳芯，等. 优选状态数的MCMC算法在风电功率序列生成中的应用[J]. 电力自动化设备，2019，39(5)：61-68.

Xu Shenzhi, Ai Xiaomeng, Zou Jiaxin, et al. Application of optimizing state number Markov chain Monte Carlo algorithm in wind power generation[J]. Electric Power Automation Equipment, 2019, 39(5): 61-68. (in Chinese with English abstract)

[29] 于佳伟，郑松林，冯金芝，等. 某轿车前副车架服役载荷模拟试验加速方法研究[J]. 机械工程学报，2016，52(22)：112-120.

Yu Jiawei, Zheng Songlin, Feng Jinzhi, et al. Research on accelerated testing method for the service-simulation fatigue test of automotive front sub-frame[J]. Journal of Mechanical Engineering, 2016, 52(22): 112-120. (in Chinese with English abstract)

Simulation of agricultural equipment load using MCMC with optimal state number

Yang Zihan, Song Zhenghe※

(,,100083,)

The selection of state number depends highly on the subjective experience in the traditional Markov Chain Monte Carlo (MCMC). However, an inappropriate value of state number can lead to a great reduction in the accuracy of load simulation, even an increase in the running time during the simulation of agricultural equipment loads. This study aims to clarify the effect of state number on the simulation when the MCMC was applied to agricultural equipment load. Specifically, the mean error, standard deviation error, and deviation of rain flow matrix between the simulated and original load decreased rapidly to stabilize, as the state number increased. Moreover, the indicators were not generalizable, if there was no significance between them. An optimization of state number was also proposed using pseudo damage consistency. As such, the damage consistency between the simulated and original load gradually improved and smoothed out, as the state number increased, whereas, the rate of increase in the operation time continued to increase. The optimal state number was calculated to satisfy the damage consistency and minimum operation time, where a threshold value was set for the pseudo damage factor. Furthermore, the field tests were carried out for both tractor ploughing and soil preparation. The specific parameters were measured to validate, including the front axle vibration, front axle stress, and driveshaft torque load. The vibration loads were also utilized to apply for the tractor front drive axle during ploughing operations. It was found that the MCMC using optimal state number can be expected torealize the load simulation with pseudo damage differences within 1%. Furthermore, there were more significant differences between the load segments in the adjustment stage, where the optimal state numbers for each load segment were more dispersed than that in the operation stage. A cyclic simulation was also developed for the loads of key components, according to the operational characteristics of a tractor. Subsequently, the MCMC cycle simulations were also performed on the front axle vibration loads for ploughing. The results show that the simulated load retained the alternating switching between the operating and adjustment stages under tractor ploughing. The same procedure was used to simulate the stress load on the front axle under ploughing, where the torque was separately loaded on the driveshaft under soil preparation. The statistical characteristic indicators were selected, including the mean, standard deviation, and the maximum load cycle amplitude for each load segment. The deviation range of each statistical eigen value was also obtained, compared with the original. The eigen values simulation for each load segment was in a higher agreement with the original eigen values. The generality was further validated when applied to the load simulation of agricultural equipment with the objective of load spectrum preparation. Consequently, the MCMC using optimal state number was better matched to the target requirements of load spectrum preparation, compared with the conventional. The finding can also effectively reduce the computational cost for the higher accuracy during load simulation of agricultural machinery.

agricultural machinery; simulation; load; Markov chain; Monte Carlo method; optimal state number; pseudo damage

2021-08-20

2021-09-30

国家重点研发计划资助项目（2017YFD0700301）

杨子涵，博士生，研究方向为农机装备载荷测试，载荷谱编制关键技术。Email：yangzihan@cau.edu.cn

宋正河，博士，教授，研究方向为农机装备试验验证方法与技术，智能化设计。Email：songzhenghe@cau.edu.cn

10.11975/j.issn.1002-6819.2021.20.002

S220

A

1002-6819(2021)-20-0015-08

杨子涵，宋正河. 利用优选状态数的MCMC 模拟农机装备负载[J]. 农业工程学报，2021，37(20)：15-22. doi：10.11975/j.issn.1002-6819.2021.20.002 http://www.tcsae.org

Yang Zihan, Song Zhenghe. Simulation of agricultural equipment load using MCMC with optimal state number[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(20): 15-22. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.20.002 http://www.tcsae.org