环量分布对基于反问题设计的混流泵优化结果的影响
李彦军,王梦成,袁建平,袁寿其,郑云浩
环量分布对基于反问题设计的混流泵优化结果的影响
李彦军,王梦成,袁建平,袁寿其,郑云浩
(江苏大学国家水泵研究中心,镇江 212013)
为定量研究叶轮出口环量分布对导叶式混流泵优化结果的影响,该研究在试验验证数值模拟准确性的基础上,以反问题设计为基础,结合最优拉丁超立方抽样法,径向基神经网络模型和多岛遗传算法,以0.8des、1.0des和1.2des处泵段加权效率为优化目标(des表示设计流量),以1.0des处扬程变化小于3%为约束条件,在自由涡设计(叶轮出口环量恒定分布)和强迫涡设计(叶轮出口环量线性变化)两种不同方案下分别对比转速为511的导叶式混流泵叶轮进行参数化优化,并对优化结果进行对比分析。研究结果表明:以轮毂处环量值作为翼展方向环量分布控制参数,结合连续性方程、能量方程和径向平衡方程,对叶轮出口处环量分布进行计算是可行的;局部敏感性分析表明环量控制参数对优化结果具有较大影响,在优化设计中应该被考虑;自由涡设计优化结果的加权效率为84.14%,而在强迫涡设计中该加权效率为85.08%,且两者扬程均满足约束条件,内流分析表明强迫涡设计中效率的提升主要由叶轮出口附近流态的改善引起。研究结果可为同类型涡轮机械的优化设计提供参考。
优化设计;混流泵叶轮;反问题设计;数值模拟;水动力参数;局部敏感性分析
0 引 言
混流泵由于其适中的扬程、较高的效率以及良好的抗空化性能被广泛应用于工业生产、农业灌溉及污水处理等领域[1-3]。然而,其理论设计体系相比于轴流泵与离心泵尚不完善[4],因此,研究其优化设计具有十分重要的意义。目前混流泵的优化设计可分为基于几何参数的传统设计与基于水动力参数的反问题设计两大类[5]。后者相比于前者具有设计参数数量少及水力性能与设计参数联系更紧密的优点。更重要的是,反问题设计中叶片角由给定的水动力参数通过迭代计算得到,相比于传统设计中通过保角变换得到的叶片角其分布形式更加多样,更有可能获得性能超出现有设计的创新型结果[6]。
反问题设计方法的有效性已在各种涡轮机械的设计优化中得到广泛证明[7-10]。Zangeneh等[11]通过调整轮毂与轮缘处流线方向载荷分布研究了载荷分布形式对混流泵性能的影响。结果表明轮缘处前加载,轮毂处后加载有利于叶片吸力面流动分离的抑制。Goto等[12]通过试验验证了上述研究的正确性。他们发现上述载荷分布形式也有利于叶轮出口处“尾迹-射流”的消除。Maillard等[13]在轴流风机的优化设计中发现给予叶片前缘适当的载荷有利于叶顶泄漏涡的提前破裂。Zhu等[14]通过调整流线载荷与轴面投影图研究了泵做透平的多目标优化。研究发现改变叶片通道内的压力梯度可以有效控制分离涡的位置。Huang等[15]以流线方向载荷分布与叶片尾缘倾角为设计参数对混流泵叶轮的设计优化进行了研究。结果表明适当的后加载有助于平滑叶片通道内的速度梯度,进而消除二次流。在另一项工作中,Ashihara等[16]发现流线方向载荷后加载有利于叶片前半部压力的提升,进而改善泵的空化性能。
虽然上述研究取得了令人满意的结果,但仍存在一定的局限性,如为控制叶轮理论扬程,在优化设计中采用自由涡来控制叶轮出口处环量分布。由Zangeneh[17]提出的叶片载荷理论可知,叶片载荷与叶轮进出口环量的分布密切相关,且张德胜等[18-19]在相关研究中指出叶轮出口处环量分布影响叶片不同叶高处的做功能力。因此,在混流泵的优化设计中,考虑翼展方向环量分布形式对混流泵优化结果的影响是必要的。
为定量研究翼展方向环量分布形式对混流泵优化结果的影响,本文以反问题设计为基础,结合最优拉丁超立方抽样、径向基神经网络模型和多岛遗传算法,在自由涡和强迫涡设计两种方案下,分别对同一混流泵模型进行参数化优化,并对优化结果进行对比分析,以期为同类型旋转机械的优化设计提供参考。
1 反问题设计理论
1.1 理论构建
本文采用由Zangeneh[20]提出的全三维反问题设计方法,在该方法中,假定流体定常无粘不可压缩,叶片对流体的作用由涡片表示,其强度(m2/s)定义为

叶片形状由流切条件计算

在此基础上给定叶轮进出口翼展方向环量分布、流线方向载荷分布及叶片尾缘处倾角即可确定叶片形状。
1.2 参数定义
叶轮做工能力由进出口翼展方向环量差确定。为满足叶轮进口流体无预旋的假设,通常假定叶轮进口处环量为0,因此,叶轮出口处环量分布与叶轮做工能力直接相关。
在之前的研究中,叶轮出口翼展方向环量被设定为恒定分布,即自由涡设计。在本研究中,为研究叶轮出口翼展方向环量分布对混流泵优化结果的影响,采用如图1所示的强迫涡设计对叶轮出口翼展方向环量分布进行参数化。
为保证在优化设计过程中叶轮理论扬程基本不变,参考汤方平和张德胜等[21-22]所提出的环量计算公式对环量分布进行估算。
由连续性方程可知
式中m为轴向速度,m/s;des为设计流量,m3/s;h和s分别为轮毂和轮缘处半径值,m。
由能量方程可知
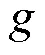
由径向平衡方程可知
记

叶片流线方向载荷分布采用如图2所示的“三段式”分布进行控制,其由两段抛物线和一段中间直线组成。图中纵坐标为载荷,横坐标为轴面流线相对位置。一般而言,叶片载荷沿轮毂与轮缘处流线方向给定,叶片其它位置的载荷值由线性插值确定。

注:m=0表示轮毂,m=1表示轮缘;NC、ND和K分别为中间直线的起始点、终止点和斜率,LE为前缘载荷值。
Zhu等[23]通过研究发现叶片尾缘处倾角对叶轮内的二次流及压力脉动幅值具有较大影响。因此,倾角也被选为设计参数。
1.3 有效性验证
在采用反问题设计方法对混流泵模型进行参数化之前需对其有效性进行验证。本文以杨魏等[24]提出的给定载荷分布与计算载荷分布的重合度作为反问题设计方法是否有效的判据,结果如图3所示。由图可知在整个流线范围内,计算载荷与给定载荷的变化趋势基本一致,两者的最大差值出现在轮缘处轴面流线相对位置0.2附近,相对误差约7%,而其他位置处相对误差均小于5%。考虑到在反问题设计中流场及叶片形状的计算均为基于无粘假设,而在CFX计算中流体的粘性被纳入计算,因此,认为上述误差在可接受范围内。
2 混流泵模型数值模拟
2.1 模型构建
以图4所示的南水北调工程中某泵站所使用的比转速为511的导叶式混流泵叶轮为基础模型,记为F0,其设计流量为0.4207 m3/s,设计扬程为12.6 m,叶片数为4个,叶轮直径为320 mm,进口轮毂与轮缘处直径分别为270 mm和20 mm,出口轮毂处与轮缘处直径分别为210 mm和370 mm。
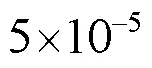
结构化网格相比于非结构化网格具有数量及质量可控的优点[25],因此,本文采用图5所示的六面体结构化网格对整体计算域进行网格划分,并在壁面处进行局部加密处理,以确保第一层网格节点与壁面之间的距离较小(即较小的+值)。其中,进水直管与出水弯管的网格划分由ANSYS-ICEM采用O型拓扑结构完成,叶轮和导叶的网格划分由ANSYS-Turbogrid采用H-C形拓扑结构完成。
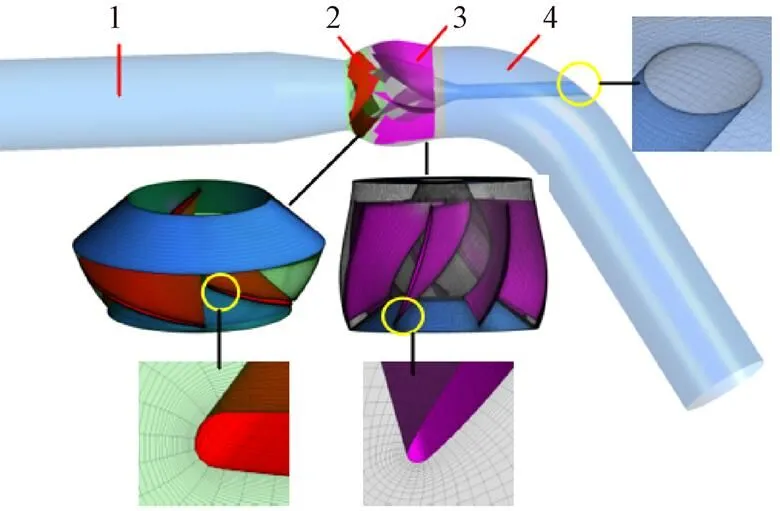
1.进水管 2.叶轮 3.导叶 4.出水管

2.2 试验验证
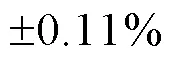
3 优化系统构建
在反问题设计方法中,叶片形状的求解与流场的求解通过迭代计算完成,因此,流场的初始化对叶片形状的求解至关重要。由于导叶的主要作用是回收叶轮出口处流体的旋转动能并将其转化为压能,因此,在导叶的优化设计中需预先求得叶轮出口处流场并将其作为进口条件。这意味着叶轮与导叶间的匹配优化最佳策略为分步优化,即先对叶轮进行优化,然后再根据优化好的叶轮对导叶进行匹配优化。本研究重点关注叶轮出口处环量分布对混流泵叶轮优化结果的影响,因此,仅以叶轮作为参数化优化对象。优化系统如图8所示,其由反问题设计、数值模拟和优化算法三部分组成,其中,反问题设计理论与数值模拟设置已在前文进行过介绍,下文将对算法选择与设置进行介绍。
3.1 设计参数
为定量研究不同涡设计对混流泵优化结果的影响,本文基于反问题设计方法,在两种不同方案下分别对F0进行参数化优化。在方案1中忽略叶轮出口翼展方向环量分布形式对混流泵优化结果的影响,故在叶轮的参数化中采用自由涡设计;而在方案2中考虑该影响,因此采用强迫涡设计对叶轮进行参数化。方案1和方案2的设计参数如表1所示。相比于方案1,方案2中叶轮出口翼展方向环量分布控制参数h也被选为设计参数。为防止反问题设计计算不收敛,无法得到正确的物理解,需保证翼展方向环量差的最大值小于均值的30%[26],因此,在本研究中,参数h的范围被定为0.27~0.35。流线方向载荷控制参数及叶片尾缘堆栈范围的选取参考文献[27]。
3.2 优化目标及约束条件
为使优化后混流泵模型与基础模型具有相似的比转速,且使其在较大的流量范围内均比基础模型具有更好的水力性能,以优化后模型1.0des处泵段扬程相比于基础模型扬程变化小于3%为约束条件1,以优化后模型0.8des、1.0des和1.2des处泵段效率相比于基础模型效率不降低为约束条件2;以上述3工况点泵段加权效率为优化目标,对混流泵叶轮进行参数化优化,权重因子按照各工况的重要性进行确定。一般而言,在混流泵的多工况优化设计中,1.0des处效率是最重要的,因此,需赋予其最大的权重值,在本研究该值为0.5;此外,由于本文研究对象为一特定调水泵站所用混流泵,其在1.2des工况运行时间与0.8des工况运行时间的比值约为3比2,因此,分别赋予1.2des和0.8des工况处0.3和0.2的权重值。约束条件的数学表达如式(8)所示,优化目标的数学表达如式(9)所示
约束条件:
优化目标:
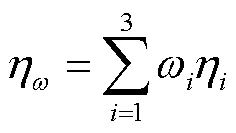
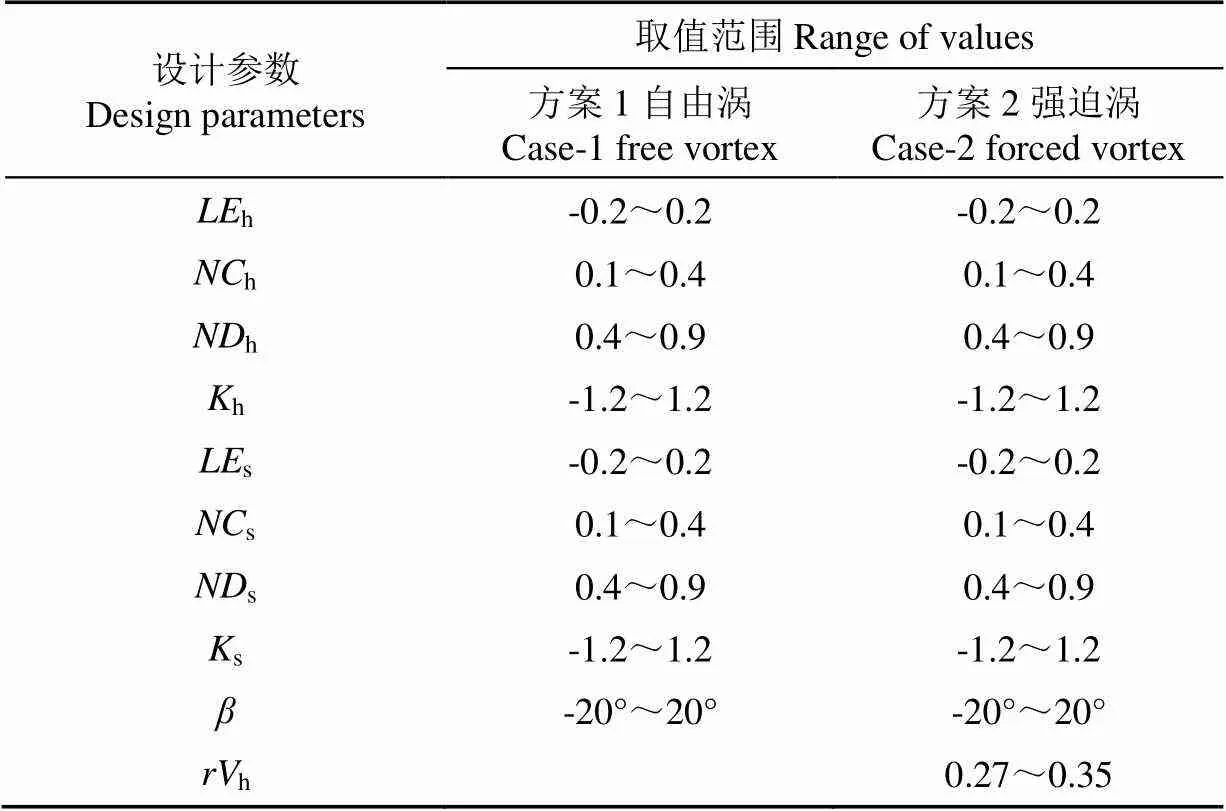
表1 自由涡设计与强迫涡设计中设计参数及范围选择
注:h表示轮毂处环量,表示叶片尾缘处倾角。下标h和s分别表示轮毂和轮缘。
Note:hmeans circulation value at the hub,means the inclination angle at the blade trailing edge; The subscripts h and s represent hub and shroud, respectively.
3.3 优化系统
3.3.1 试验设计
最优拉丁超立方抽样法可将设计空间划分为设计者指定的层数,并对每层进行独立随机抽样,具有抽样效率高,空间填充能力强,及样本空间与设计空间结构相似的优点。因此,两种方案下均使用最优拉丁超立方抽样法在设计空间中生成110个样本点。考虑到方案2中设计参数包含翼展方向环量分布控制参数,为了提高近似模型扬程预测准确性,需要对各样本点设计工况扬程进行监测,从而剔除扬程波动过大(10%设计点处泵段扬程)的样本点,并增加新样本点。

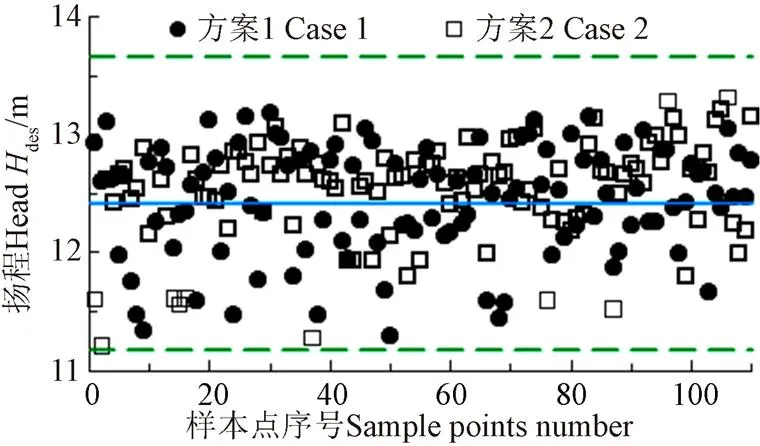
注:实线为设计工况处F0的泵段扬程,虚线为所允许的扬程变化极限。
3.3.2 近似模型
近似模型可用于构建设计参数与优化目标之间的映射关系,其可有效减少优化过程中数值模拟的调用次数,从而减少计算资源的消耗。径向基神经网络模型[28]是一种单隐层前馈神经网络模型,由输入层、隐藏层和输出层组成。其中输入层到隐藏层为非线性变换,而隐藏层到输出层为线性变换,其基本原理见文献[29]。由于其良好的非线性逼近能力,在优化设计中得到了广泛的应用。因此,本文采用该神经网络模型构建设计参数与优化目标之间的函数关系,其中,滤波算子设定为0.02,最大迭代次数为50,激活函数选用高斯函数。
3.3.3 优化算法
最优解的寻找由多岛遗传算法完成,与传统遗传算法相比,其不仅拥有交叉、变异和选择等操作,还额外引入了“岛”这一理念。在该算法中,整个种群被划分为若干个子群(岛),通过在各子群间执行交叉、变异和选择,并周期性的在各个子群间进行相应的迁徙,保持解的多样性,从而避免传统遗传算法早熟收敛的缺点。在本研究中,优化算法的设置在两种方案下保持一致,初始种群数均为50,种群代数为20,岛屿数为10,交叉概率为0.75,变异概率为0.1。因此,两种方案下各生成了10 000种不同配置的叶轮。
4 优化结果与分析
4.1 优化结果
方案1与方案2的迭代计算过程如图10所示。相比于方案1,方案2在经过若干次迭代计算后更易获得加权效率更高的叶轮配置。分别记两种方案下满足约束条件且加权效率最高的叶轮配置为F1与F2。两者设计参数及叶片外形对比分别如表2和图11所示。相比于F1,F2的设计参数及叶片外形均出现了较大变化,因此,在混流泵的优化设计中,有必要考虑叶轮出口翼展方向环量分布形式。
为验证近似模型预测准确性,对优化后模型F1与F2分别进行数值模拟分析,结果如表3所示。由表3可知F1和F2加权效率的计算值与预测值相差较小,且均满足约束条件要求。F1加权效率的计算值为84.14%,相比于F0,该加权效率增加了2.55个百分点,而F2的加权效率则在F1的基础上进一步提高了0.94个百分点。因此,在基于反问题设计的混流泵的优化设计中,采用强迫涡设计相比自由涡设计更具优势,可以进一步提升优化效果。

表2 F1与F2设计参数对比
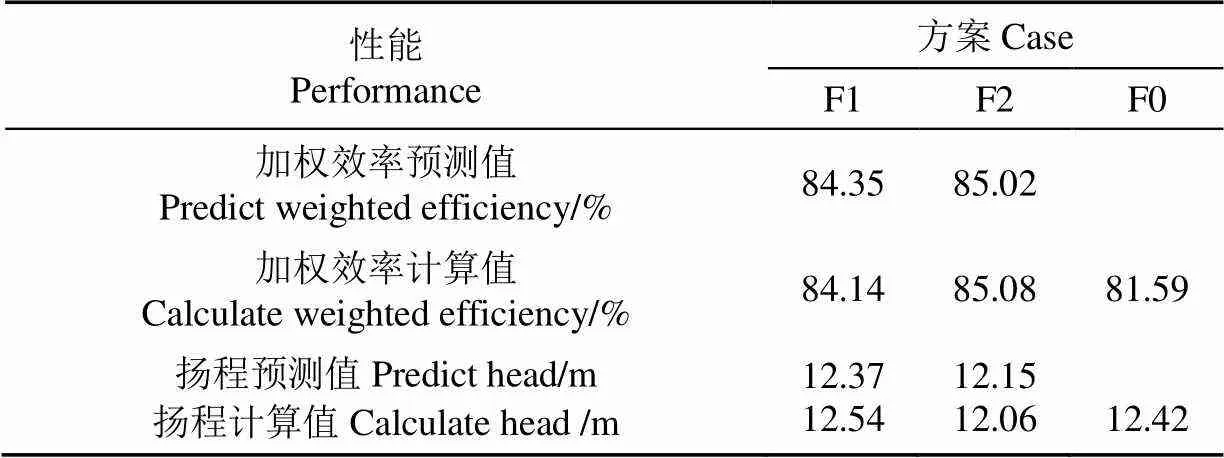
表3 计算性能与预测性能对比
F0、F1与F2的外特性对比如图12所示。在整个流量范围内,F2的泵段效率最高,F1次之,且随着流量增加,三者间的差值逐渐增大。以0.8des、1.0des和1.2des处泵段效率为例,F0的泵段效率为80.59%、85.31%和76.07%,F1的泵段效率相比于F0分别增加了0.06、2.54和4.22个百分点,而F2的泵段效率则在F1的基础上进一步增加了0.59、0.87和1.39个百分点。三者的扬程也出现了较大的区别。在设计工况处,三者扬程基本相同。然而在小流量工况处,F0的扬程最大,而F1和F2的扬程基本相等,且随着流量的减小,F0与F1和F2的扬程差逐渐增大。在大流量工况处,F1的扬程最大,而F2与F0的扬程基本相等。
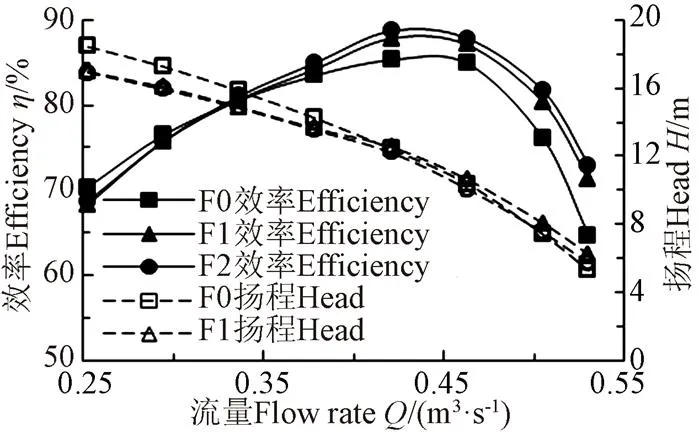
图12 优化结果外特性对比
4.2 性能分析
为分析F0、F1与F2性能差异产生的原因,以设计工况为例,对三者的内流场进行进一步对比分析。
图13展示了三种模型叶轮出口轴向速度和总压沿展向分布的对比。由图13a可知F0轮毂附近(*=0处)轴向速度为负值且在较大的范围内轴向速度处于较低的水平,这意味着该处出现了小范围的回流区及较大范围的低速区。经过优化后,F1与F2在轮毂处的轴向速度相比于F0得到了巨大的提升,从而消除了该低速回流区的存在。轮毂附近轴向速度的增加与轮缘附近轴向速度的减小使得F1与F2在整个翼展方向的轴向速度分布相比于F0更加均匀。在图13b中的翼展方向总压分布观察到了类似的现象,这表明F1与F2在叶轮出口处的流态相比于F0得到了改善。此外,相比于F1,F2在轮毂附近的轴向速度与总压略有降低,而轮缘附近的轴向速度与总压略有升高,该趋势与叶轮出口处翼展方向环量分布形式相一致,表明在混流泵的优化设计中采用强迫涡设计可以有效控制叶轮出口处的流态。
图14为叶轮出口叶片吸力面轮毂附近速度矢量和静压分布图。由图14可知F0在叶片出口轮毂附近产生了明显的回流现象,考虑到该区域内静压分布相对均匀且压力梯度与主流方向基本一致,结合图13a中F0在叶轮出口轮毂附近轴向速度为负值且在较大范围内存在低速区的事实,分析认为该回流是由低动量流体的聚集所导致的边界层脱落引起的,且该回流对叶轮出口处的流态产生了不利影响。此外,该回流与轮毂附近主流的互相作用迫使主流向跨中方向偏转,导致了叶片尾缘附近二次流的产生。在F1的叶片吸力面尾缘处也观察到了相似的回流和二次流现象,然而其形成机理与F0相比存在较大区别,且其对叶轮内部流场的影响也存在较大区别。在F1中,尽管轮毂附近的轴向速度最大,可以有效防止低动量流体的聚集,抑制边界层的生长,然而由于该区域内的静压分布存在着明显的畸变,且压力梯度垂直于主流方向,从而导致该区域内回流与二次流的出现。然而,相比于F0,F1中的回流与二次流对叶轮内部流态的影响在到达叶轮出口处之前已被消除。在F2中,由于轮毂附近轴向速度较大,且压力梯度与主流方向几乎一致,因此,该区域内的流态得到了明显改善。
考虑到叶轮出口流态对叶轮下游部件的水力性能具有较大影响,而F0、F1与F2中叶轮出口的流态又存在较大区别,因此有必要对三者下游部件的水力性能进行分析,以确定泵段整体性能提升的原因。表4为各部件的水力损失与总输入功率的比值。由表可知F0在设计工况处的叶轮效率为95.04%,已处于较高的水平,然而由于叶轮出口附近存在脱流现象,导致叶轮下游部件出现了较大的水力损失。经过优化后,在F1中,尽管叶轮内的水力效率损失仅降低0.11个百分点,然而由于出口流态的改善,叶轮下游部件的水力效率损失降低了2.43个百分点。与F1相比,F2中叶轮的水力效率损失进一步降低了0.59个百分点,而叶轮下游部件的水力效率损失则进一步降低了0.28个百分点。

表4 水力效率损失分析
4.3 参数敏感性分析
在优化设计中,与优化目标相关性较大的设计参数应该被重点考虑以提高优化效果,而相关性较小的设计参数则可以被忽略,从而降低优化复杂度,加快优化进程。局部敏感性分析通过求解各设计参数对优化目标的偏导数来确定各参数对优化目标的影响程度,因其良好的可操作性和较低的操作复杂度被广泛应用于各种优化设计中。本文所构建的近似模型的准确性已在3.1节中得到验证,因此,在此基础上进行的局部敏感性分析是可靠的。
图15为局部敏感性分析结果。在方案1中,、s、h、h和s对优化目标影响较大,而h、s、h和s对优化目标影响较小,且h、s、h和h为正影响,其余参数为负影响。在方案2中,h、s、h、h、h、s和s对优化目标影响较大,h、和s对优化目标影响较小,且h、h、h和h为负影响,其余参数为正影响。相比于方案1,方案2中各参数对优化目标的影响程度及正负关系均产生了较大改变。因此,在强迫涡设计中,设计参数的选择将与自由涡设计产生较大区别。
5 结 论
本文以反问题设计为基础,通过连续性方程、能量方程与径向平衡方程完成了叶轮出口翼展方向环量分布的参数化,并在此基础上通过数值模拟与优化算法相结合的方法探究了环量分布对混流泵优化结果的影响。结果表明:
1)与自由涡设计相比,在强迫涡设计中各样本点在设计工况处的扬程波动无明显增加,且优化结果表明,强迫涡设计中优化结果F2的加权效率相比于自由涡设计优化结果F1进一步提高了0.94%,因此在基于反问题设计的混流泵优化设计中,考虑翼展方向环量分布对优化结果的影响是可行且必要的。
2)通过控制叶轮出口处翼展方向环量分布可有效控制叶轮出口附近流态,防止回流等不利流动的产生,进而改善叶轮出流条件。
3)内流分析及水力损失分析结果表明,F2相比于F1效率的提升主要由两方面所引起。一是叶轮出口吸力面轮毂附近回流的抑制,二是叶轮出口流态的改善所导致的下游部件水力损失的减小。
[1] Li W, Ji L L, Shi W D, et al. Vibration of shaft system in the mixed-flow pump induced by the rotor-stator interaction under partial load conditions[J]. Shock and Vibration, 2018(2): 1-12.
[2] Tan L, Yu Z Y, Xu Y, et al. Role of blade rotational angle on energy performance and pressure fluctuation of a mixed-flow pump[J]. Proceedings of the Institution of Mechanical Engineers Part A Journal of Power and Energy, 2017, 231(3): 227-238.
[3] 李伟,路德乐,马凌凌,等. 混流泵启动过程压力脉动特性试验[J]. 农业工程学报,2021,37(1):44-50.
Li Wei, Lu Dele, Ma Lingling, et al. Experimental study on pressure vibration characteristics of mixed-flow pump during start-up[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(1): 44-50. (in Chinese with English abstract)
[4] 潘中永,倪永燕,袁寿其,等. 斜流泵研究进展[J]. 流体机械,2009,37(9):45-49.
Pan Zhongyong, Ni Yongyan, Yuan Shouqi, et al. Research progress of mixed-flow pump[J]. Fluid Machinery, 2009, 37(9): 45-49. (in Chinese with English abstract)
[5] 肖若富,陶然,王维维,等. 混流泵叶轮反问题设计与水力性能优化[J]. 农业机械学报,2014,45(9):84-88.
Xiao Ruofu, Tao Ran, Wang Weiwei, et al. Inverse design and hydraulic optimization of mixed-flow pump impeller[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(9): 84-88. (in Chinese with English abstract)
[6] Goto A, Zangeneh M. Hydrodynamic design of pump diffuser using inverse design method and CFD[J]. Journal of Fluids Engineering, 2002, 124: 319-328.
[7] 邴浩,曹树良,谭磊. 混流泵叶轮设计正反问题迭代方法[J]. 排灌机械工程学报,2011,29(4):277-281.
Bing Hao, Cao Shuliang, Tan Lei. Iteration method of direct inverse problem of mixed-flow pump impeller design[J]. Journal of Drainage and Irrigation Machinery Engineering, 2011, 29(4): 277-281. (in Chinese with English abstract)
[8] 王福军,姚志峰,杨魏,等. 双吸离心泵叶轮交替加载设计方法[J]. 农业机械学报,2015,46(6):84-91.
Wang Fujun, Yao Zhifeng, Yang Wei, et al. Impeller design with alternate loading technique for double-suction centrifugal pumps[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(6): 84-91. (in Chinese with English abstract)
[9] 杨魏,王福军,王宏. 离心风机叶片三维反问题优化设计[J]. 农业机械学报,2012,43(8):105-109.
Yang Wei, Wang Fujun, Wang Hong. Aerodynamic optimization design of centrifugal fan blades based on 3-D inverse design method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(8): 105-109. (in Chinese with English abstract)
[10] Zangeneh M. A compressible three-dimensional design method for radial and mixed flow turbomachinery blades[J]. International Journal for Numerical Methods in Fluids, 1991, 13(5), 599-624.
[11] Zangeneh M, Goto A, Takemura T. Suppression of secondary flows in a mixed-flow pump impeller by application of three-dimensional inverse design method: Part 1-design and numerical validation[J]. Journal of Turbomachinery, 1996, 118(3), 536-543.
[12] Goto A, Takemura T, Zangeneh M. Suppression of secondary flows in a mixed-flow pump impeller by application of three-dimensional inverse design method part 2-experimental validation[J]. Journal of Turbomachinery, 1996, 118(3), 544-551.
[13] Maillard M D, Zangeneh M. Application of 3d inverse design based multi-objective optimization of axial cooling fan with large tip gap[J]. Sea Technical Papers, 2014, 1, 415-422.
[14] Zhu B S, Wang X H, Tan L, et al. Optimization design of a reversible pump-turbine runner with high efficiency and stability[J]. Renewable Energy, 2005, 81, 366-376.
[15] Huang R F, Luo X W, Ji B, et al. Multi-objective optimization of a mixed-flow pump impeller using modified NSGA-II algorithm[J]. Science China Technological Sciences, 2015, 58, 2122–2130.
[16] Ashihara K, Goto A. Effects of blade loading on pump inducer performance and flow fields[C]. Proceedings of the ASME 2002 Joint U. S. -European Fluids Engineering Division Conference. Volume 2: Symposia and General Papers, Parts A and B. Montreal, Quebec, Canada, July, 14–18, 925-934. ASME.
[17] Zangeneh M, Goto A, Harada H. On the design criteria for suppression of secondary flows in centrifugal and mixed flow impellers[J]. Journal of Turbomachinery, 1997, 120(4): 723-735.
[18] 张德胜,施卫东,李通通,等. 轴流泵叶轮非线性环量数学模型建立与试验[J]. 农业机械学报,2013,44(1):58-61.
Zhang Desheng, Shi Weidong, Li Tongtong, et al. Establishment and experiment on nonlinear circulation mathematical model of axial-flow pump impeller[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1): 58-61. (in Chinese with English abstract)
[19] 张德胜,李通通,施卫东,等. 轴流泵叶轮出口轴面速度和环量的试验研究[J]. 农业工程学报,2012,28(7):73-77.
Zhang Desheng, Li Tongtong, Shi Weidong, et al. Experimental investigation of meridional velocity and circulation in axial-flow impeller outlet[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(7): 73-77. (in Chinese with English abstract)
[20] Zangeneh M. Inviscid-viscous interaction method for three-dimensional inverse design of centrifugal Impellers[J]. Journal of Turbomachinery, 1994, 116(2): 280-290.
[21] 张德胜. 轴流泵叶轮非线性环量分布理论及实验研究[D]. 镇江:江苏大学,2010.
Zhang Desheng. Theoretical and Experimental Research on Nonlinear Circulation Distribution of Axial Pump Impeller[D]. Zhenjiang: Jiangsu University, 2010. (in Chinese with English abstract)
[22] 汤方平. 喷水推进轴流泵设计及紊流数值分析[D]. 上海:上海交通大学,2006.
Tang Fangpin. Design and Turbulence Numerical Analysis of Water jet Axial-Flow Pump[D]. Shanghai: Shanghai Jiaotong University, 2010. (in Chinese with English abstract)
[23] Zhu B S, Tan L, Wang X H, et al. Investigation on flow characteristics of pump-turbine runners with large blade lean[J]. Journal of Fluids Engineering, 2018, 140(3): 1113-1122.
[24] 杨魏,雷晓宇,张志民,等. 基于载荷分布的潜水轴流泵叶轮与导叶水力设计[J]. 农业机械学报,2017,48(11):179-187.
Yang Wei, Lei Xiaoyu, Zhang Zhimin, et al. Hydraulic design of submersible axial-flow pump based on blade loading distributions[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(11): 179-187. (in Chinese with English abstract)
[25] 李志祥,冯建刚,钱尚拓,等. 排水泵站整流底坎参数优化[J]. 农业工程学报,2021,37(3):56-63.
Li Zhixiang, Feng Jiangang, Qian Shangtuo, et al. Optimization of rectification bottom sill parameters in drainage pumping stations[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(3): 56-63. (in Chinese with English abstract)
[26] 王梦成,李彦军,袁建平,等. 叶轮出口环量非线性分布条件下混流泵性能研究[J]. 农业机械学报,2020,51(11):211-218.
Wang Mengcheng, Li Yanjun, Yuan Jianping, et al. Performance of mixed flow pump under condition of non-linear distribution of impeller exit circulation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(11): 211-218. (in Chinese with English abstract)
[27] 王梦成,袁建平,李彦军,等. 混流泵叶轮三维反问题设计多目标优化[J]. 哈尔滨工程大学学报,2020,41(12):1854-1860.
Wang Mengcheng, Yuan Jianping, Li Yanjun, et al. Multi-objective optimization of mixed-flow pump impeller based on 3-D inverse design[J]. Journal of Harbin Engineering University, 2020, 41(12): 1854-1860. (in Chinese with English abstract)
[28] 王春林,胡蓓蓓,冯一鸣,等. 基于径向基神经网络与粒子群算法的双叶片泵多目标优化[J]. 农业工程学报,2019,35(2):25-32.
Wang Chunlin, Hu Beibei, Feng Yiming, et al. Multi-objective optimization of double vane pump based on radial basis neural network and particle swarm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(2): 25-32. (in Chinese with English abstract)
[29] 吴月宝,赵晋斌,张少腾,等. 基于径向基神经网络的多负载无线电能传输系统自适应阻抗匹配方法[J]. 电工技术学报,2021,36(19):3969-3977.
Wu Yuebao, Zhao Jinbin, Zhang Shaoteng, et al. An adaptive impedance matching method based on radial basis function neural network in multi-Load wireless power transfer Systems[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 3969-3977. (in Chinese with English abstract)
Influence of circulation distribution on the optimization results of mixed-flow pump based on inverse design
Li Yanjun, Wang Mengcheng, Yuan Jianping, Yuan Shouqi, Zheng Yunhao
(,,212023,)
To quantitatively study the influence of the impeller outlet circulation distribution on the optimization results of the mixed flow pump, the mixed flow pump with a specific speed of 511 was selected as the baseline model. A comprehensive optimization system was used to optimize under two different conditions, and the performance of the optimization results were compared with the baseline model. In the first case, the influence of the distribution form of the impeller outlet circulation on the optimization result of the mixed flow pump impeller was not considered, that is, the free vortex design (constant distribution of impeller outlet spanwise circulation) was adopted, while in the second case, the effect of circulation distribution was considered, and the forced vortex design (linear distribution of impeller outlet spanwise circulation) was adopted. The optimization system consists of an inverse design method, an optimal latin hypercube sampling method, a radial basis function neural network model and a multi-island genetic algorithm. The optimization objective is the weighted efficiency at 0.8des, 1.0desand 1.2deswith weighting factors of 0.2, 0.5, and 0.3 (desmeans design flow rate). The constraints are the head change of the optimized mixed flow pump at 1.0desless than 3% compared to the baseline model design point, and the pump section efficiency at 0.8des, 1.0desand 1.2desis greater than the baseline model. The research results showed that in the forced vortex design, when the circulation value at the hub was selected as the design parameter, it is feasible to combinedly use the continuity equation, the energy conservation equation and the radial balance equation to calculate the spanwise distribution of impeller outlet circulation. Which can ensure that the pump section head changes of the sampling points under the design condition are within a reasonable range (the range of head variation is less than 10% of the baseline model design head), and there is no need to add new sample points. In addition, the comparison of the predicted head and calculated head of the optimal solution also shows the same result. The results of local sensitivity analysis showed that the impeller outlet spanwise circulation distribution control parameters has a greater impact on the pump section weighted efficiency, and it can influence the other design parameters effect on the weighted efficiency. Therefore, it is necessary to consider the influence of the impeller outlet circulation in the optimal design of the mixed flow pump. The internal flow analysis showed that the forced vortex design can more effectively control the flow regime near the impeller outlet than the free vortex design. This is not only conductive to the improvement of the efficiency of the impeller, but also to the reduction of the hydraulic loss of the downstream components of the impeller, thereby further improving the overall optimization effect of the mixed flow pump. In the free vortex design, the weighted efficiency of the optimization result is 84.14%, while in the forced vortex design, the weighted efficiency of the optimization result is 85.08%, and the heads of both all meet the constraint conditions. This study can provide reference for the optimization design of turbomachinery, so as to maximize the optimization effect.
optimization design; mixed-flow pump impeller; inverse design; numerical simulation; hydrodynamic parameters; local sensitivity analysis
李彦军,王梦成,袁建平,等. 环量分布对基于反问题设计的混流泵优化结果的影响[J]. 农业工程学报,2021,37(20):44-52.doi:10.11975/j.issn.1002-6819.2021.20.005 http://www.tcsae.org
Li Yanjun, Wang Mengcheng, Yuan Jianping, et al. Influence of circulation distribution on the optimization results of mixed-flow pump based on inverse design[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(20): 44-52. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2021.20.005 http://www.tcsae.org
2021-06-29
2021-09-29
国家重点研发计划项目(2018YFB0606103);武汉市科技计划项目(2018060403011350).
李彦军,博士,副教授,硕士生导师,研究方向为水泵及水泵站的工程优化。Email:lyj782900@ujs.edu.com
10.11975/j.issn.1002-6819.2021.20.005
TH313
A
1002-6819(2021)-20-0044-09

