基于超椭球贝叶斯网络的制动系统可靠性研究
齐金平,周亚辉,李少雄,王 康
(1. 兰州交通大学 机电技术研究所,甘肃 兰州 730070;2. 甘肃省物流及运输装备信息化工程技术研究中心,甘肃 兰州 730070; 3. 甘肃省物流与运输装备行业技术中心,甘肃 兰州 730070)
0 引 言
近年来,中国高铁发展速度迅猛,截止2019年末,运营里程已占世界总里程70%以上,载客量增长率上升明显,运输里程持续增长,动车组的安全可靠性已成为备受关注的指标之一,维修压力也日益上升。制动系统作为动车组主要子系统之一,直接决定着运营安全,且制动系统功能层次结构复杂,同时受多因素影响,如环境、维修等,是典型的多失效状态系统。近年来,一些专家学者对制动系统进行了研究,郭济鸣等[1]以基于Markov模型的故障树为基础,对制动系统进行了可靠性分析;陈蓝等[2]对气动控制单元建立故障树进行分析,并对其不可靠度进行了预测;钱盈等[3]建立基础制动系统GO图并进行定量评估。以上分析建模方法简单,只能对整个系统分析,且不能双向推理。
贝叶斯网络(Bayesian network)的优势在处理复杂系统中的可靠性问题时得到了凸显,出现了离散、模糊、动态等贝叶斯网络,付果[4]以贝叶斯网络为起点,为可靠性评估提供了更多信息;李硕[5]基于液压系统的特性,提出离散贝叶斯网络的建模方法;张瑞军等[6]以模糊子集为基础,区间三角模糊多态贝叶斯网络得以构建;李文杰等[7]使用贝叶斯网络方法和模糊数学理论,建立了航道整治建筑物技术状况的综合评价模型;张重阳等[8]将贝叶斯网络理论应用于路网形态特征之中,构建量化路网抗震可靠性的贝叶斯网络模型并求解。但是,现实工程数据缺失,以及模糊模型及概率模型对数据的强依赖性,使贝叶斯网络在处理实际问题时未能充分发挥作用,且贝叶斯网络节点失效区间取极值的可能性几乎不会发生。
凸模型处理复杂系统不确定问题的能力显著,且可以弥补概率模型和模糊模型不足,使其在可靠性分析中优势独特,超椭球模型是凸模型的一种特殊情况,它能提高区间分析精度,规避区间出现极值情况。陈东宁等[9]结合椭球模型对液压系统进行可靠性评估;葛轶等[10]引入椭球模型,结合贝叶斯网络构建新模型,并以配电系统为例验证实用性。以上研究多以2种故障状态分析为主,对多状态、多失效模式分析较少,对贝叶斯网络的应用也主要从方法本身出发进行分析。笔者以超椭球模型对区间变量进行约束,结合贝叶斯网络,构建超椭球贝叶斯网络模型,提高了区间精度,一定程度上解决区间保守问题,并将其引入动车制动可靠性分析中,通过求解制动系统的灵敏度、后验概率等重要参数,以期找出系统的薄弱环节和影响制动系统可靠性的高风险事件,为检修策略的制定及技术改造提供理论指导。
1 基本概念
1.1 超椭球贝叶斯网络

(1)

引入矢量z使根节点的失效可能性落在式(1)的超椭球域内,表述为式(2)~式(4):
z=D-1Q
(2)
(3)
(4)
故而式(1)表述为新的超椭球模型:
(z-z0)T(z-z0)≤1
(5)
(6)
根据式(5),根节点失效在Δz=z-z0的超椭球空间内部随机取值,假如(r,θ1,θ2,…,θn-1),r∈[0,1],θi∈[0,2π]为单位超椭球的坐标,则xi的失效可能性表述为:
(7)
1.2 后验概率与灵敏度
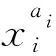
(8)
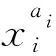
(9)
其中:
(10)
根节点xi相对于叶节点T的灵敏度为:
(11)
式中:ki为xi故障状态的数量。
2 动车组制动系统可靠性分析
制动系统主要包括电制动和空气制动2大部分,空气制动又由基础制动部分、制动控制部分、空气供给系统3个子系统构成,其结构简图如图1。

图1 制动系统结构Fig. 1 Braking system structure
根据图1及文献[9]中制动系统构成与运行原理,构建BN如图2。各节点具体含义见表1。
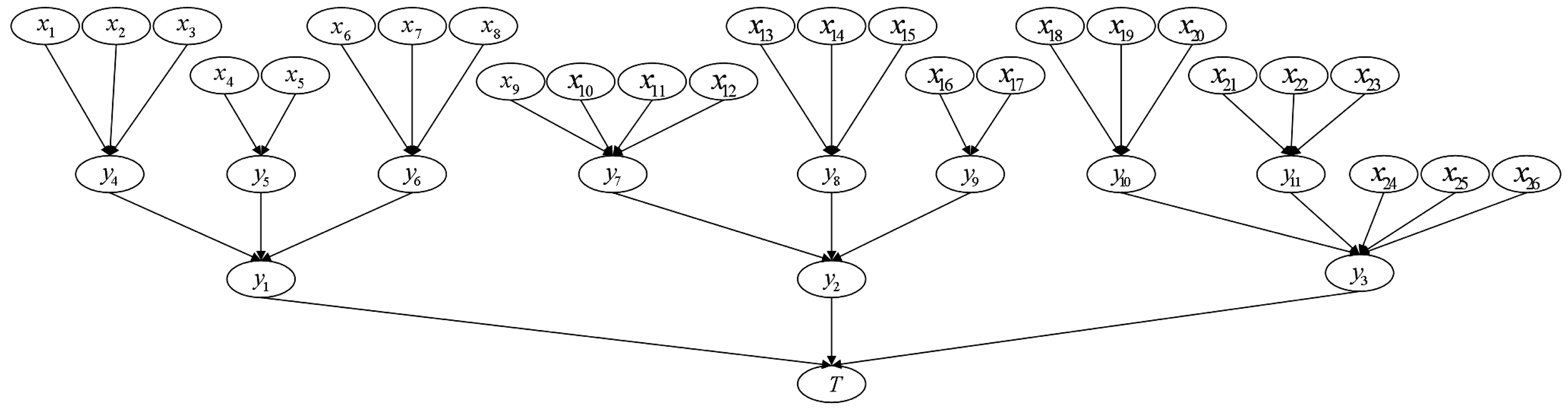
图2 制动系统贝叶斯网络Fig. 2 Brake system Bayesian network

表1 节点含义Table 1 Node implications
由文献[10]中某铁路局运行故障数据,采用信心指数修正的专家调查法,并结合三角模糊数进行处理分析,可得部分节点失效可能性区间如表2。

表2 节点失效可能性区间Table 2 Node failure probability interval
其中x1~x6,x21~x24为2种故障状态,其余为3种故障状态,假设0表示无故障状态,0.5表示半故障状态,1表示完全故障状态。由文献[11]及以上结果,得中间节点y5条件概率表如表3。表3中,规则1表示在x4,x5无故障状态下y5故障概率为0。

表3 中间节点y5的条件概率Table 3 Conditional probability tables for intermediate nodes y5
假设各基本事件故障状态为0.5的故障概率与故障状态为1的故障概率相同,由表2、表3、式(7)、以及贝叶斯网络上级事件失效可能性计算公式可得中间节点的失效可能性:
P(y6=0.5)=P8×t9+P8×t7+P7×t8+P7×t8+P6×t7=[84.098,96.058]×10-6
(12)
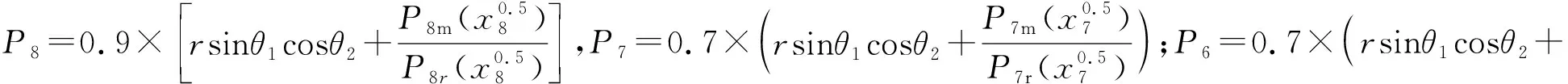

其余节点失效可能性如表4。由表4可知:无论是故障状态为0.5还是故障状态为1,超椭球贝叶斯概率区间更小,精度更高。
同理,结合表4可得:
P(T=[0,1])=(34.874,38.632)×10-6,
P(T=1)=(154.279,159.578)×10-6。
由式(8)及上述结果,对贝叶斯网络反向推理,得各节点后验概率如表5,后验概率大的部件为系统薄弱环节。
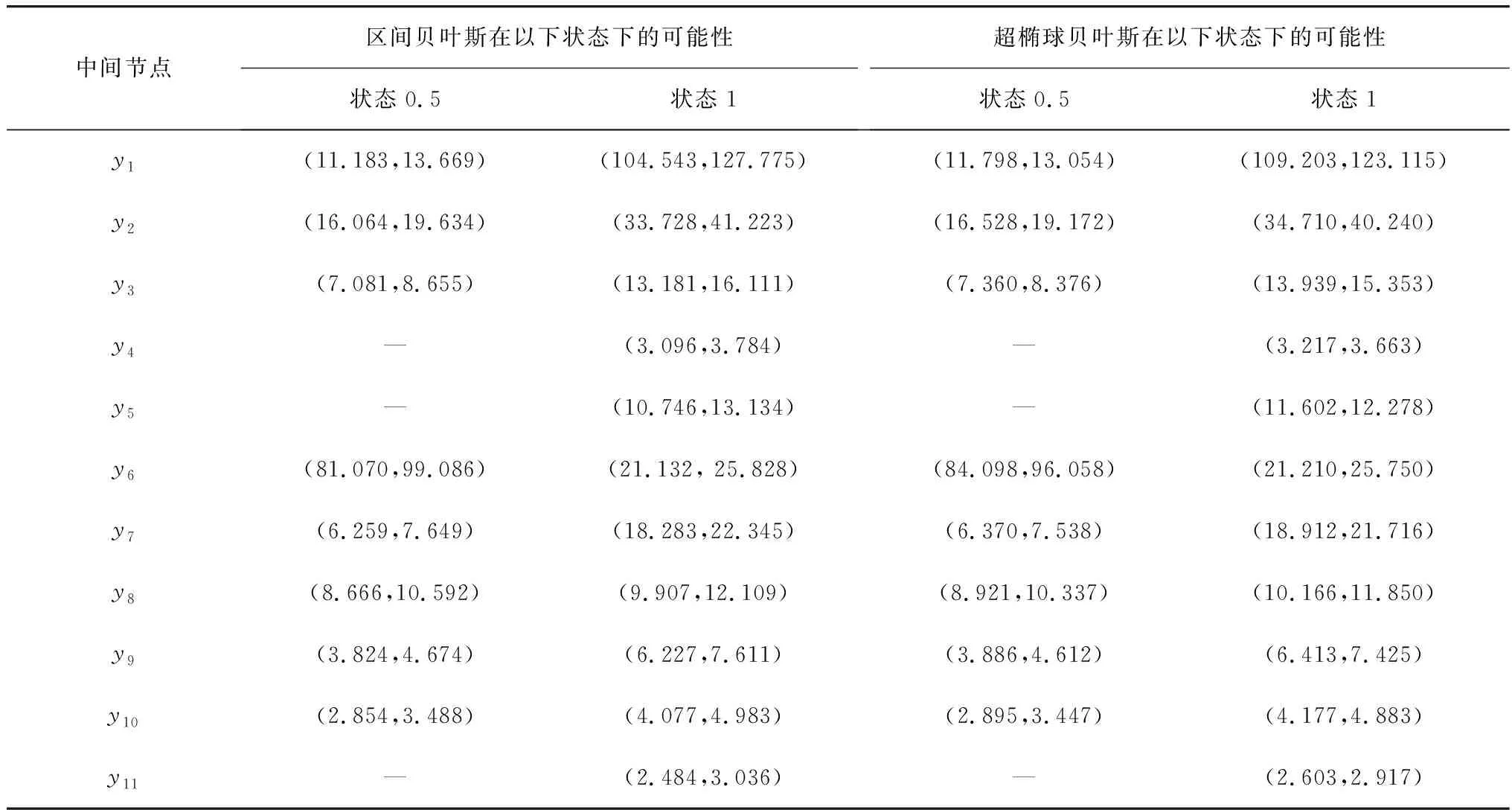
表4 中间节点失效可能性(10-6)Table 4 Intermediate node failure probability

表5 后验概率表(10-6)Table 5 Posteriori probabilities
由式(9)~式(11),可得节点灵敏度中值为:
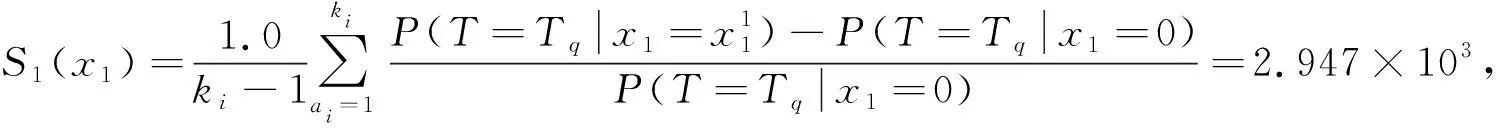
由图3可知:x8、x16、x17在系统轻微故障时灵敏度大,x7、x6在系统完全故障时灵敏度较大,均为风险高的事件,应该侧重检修。由表(5)可知:系统轻微故障时,x11,x14后验概率较大,系统完全故障时,x7后验概率最大,为系统的薄弱环节。这与实际相符,主要原因是闸片由于过度磨损,常出现缺陷和裂纹,而风管又容易被砂石等击打而导致破裂漏风,空气压缩机经常使用容易出现渗油等现象,因而故障率也较高,应根据分析结果合理安排维修频次。

图3 灵敏度数值Fig. 3 Sensitivity value
3 结 语
1)制动系统是典型的多状态、多失效模式系统,构建超椭球贝叶斯网络模型,描述各节点的多种故障状态,更加符合现场实际情况。
2)以贝叶斯网络为基础,结合超椭球模型约束根节点的取值范围,解决了区间贝叶斯网络分析结果保守问题,可靠性分析精度得以提高。
3)利用超椭球贝叶斯网络的双向推理能力,求解制动系统的灵敏度、后验概率等重要参数,找出了系统的薄弱环节以及影响系统可靠性的高风险事件,为检修策略的制定提供理论指导。

