螺旋带状整地装置功耗分析与试验研究

许春林，恒勇奇，李 峥，薛向磊，王金武*

（1.东北农业大学工程学院，哈尔滨 150030；2.浙江省农业科学院农业装备研究所，杭州 310021）

土壤耕整作业是农业生产过程重要环节[1-2]。旋耕为平原地区主要耕作方式，可一次性完成耕耙作业，且耕后表土细碎、地表平整，但存在能耗高、土壤扰动大等问题[3-4]。近年学者通过理论减阻、振动减阻和仿生减阻等技术虽降低一定旋耕耕作阻力[5-7]，但旋耕产生的抛土功耗大和土壤扰动大等问题并未解决。许春林等研制斜置式螺旋带状整地装置，以带状整地代替全幅整地、以螺旋整地代替旋耕整地为上述问题提供解决方案[8]。功率消耗是衡量整地装置综合性能重要参数[9]，研究斜置式螺旋带状整地装置作业功耗，对优化装置结构参数、机具配套动力和减阻降耗等具有重要价值。

传统耕作部件功耗试验通常在田间或室内土槽试验台上完成。田间试验可直接反应耕作机具实际性能和土壤响应，但存在控制精度差、土壤环境因素不可控等缺点[10]。离散元法可有效解决耕作部件与土壤相互作用的非线性问题，获取田间试验缺少的数据信息，实现耕作部件性能预测及参数优化，成为当前农机具研究重要辅助手段。祝英豪等基于离散元法，构建稻板田旋耕功耗预测模型，用以辅助旋埋刀辊功耗检测[11]；胡建平等基于离散元法，构建双轴旋耕—秸秆—土壤耕作模型，研究双轴配置参数对功耗影响，通过响应面分析，建立功耗数学预测模型[12]；Zhao等采用离散元法模拟不同刃口曲线旋耕刀作业时扭矩要求和土壤扰动特性，结果表明随刃口滑切角增加，作业所需扭矩和土壤扰动量均减小[13]。

本文根据东北地区土壤特性及螺旋带状整地装置作业特点，分析螺旋带状整地装置作业功耗和土壤扰动，得到螺旋带状整地装置作业功耗与结构参数、工作参数、土壤物理及力学性质函数关系。通过离散元法建立该装置功耗模型，明确入土角度、转速、作业速度等因素对作业功耗影响，并通过土槽试验验证，以期为螺旋带状整地装置结构优化、动力合理配套和功耗特性研究等提供参考。

1 结构与原理

螺旋带状整地装置的螺旋叶片用4 mm钢板经模具冷压而成，焊接于螺旋带状整地装置刀轴，螺旋叶片左旋。整地作业由螺旋叶片绕自身轴线圆周运动（相对运动）及随机组前进直线运动组成。与旋耕刀长幅摆线运动不同[14]，螺旋带状整地装置绝对运动轨迹为螺旋线。操作人员可根据农艺和作业要求调解螺旋整地装置入土角（见图1中θ所示）调节耕深。如图1所示，当机具作业时，螺旋叶片可随机具以速度V前行作进给运动切入正前方土壤，也可以角速度绕自身轴线作圆周运动，挤压被切土壤并切下土垡；两种运动共同作用于土层作切削。

图1 作业示意图Fig.1 Tillage schematic

切削后土壤由于受离心力、重力、螺旋叶片法向力（法向力可分解为轴向分力和径向分力）、摩擦力等共同作用，产生两种状态：土壤颗粒所受离心力（惯性力）大于其他力合力时，土壤颗粒被螺旋叶片抛出；土壤颗粒所受离心力（惯性力）小于其他力合力时，随螺旋叶片一起旋转，并在螺旋叶片法向推力的轴向分力及摩擦力作用下向后运动。土壤颗粒在被螺旋叶片抛出和向后推送过程中，和沟壁、螺旋叶片及其他土壤颗粒碰撞，导致土壤破碎。螺旋叶片推动土块向后运动，不仅完成推土整地作业，同时产生的轴向力也可减小拖拉机对机具的牵引阻力。图2为扰动后土壤分布和耕作带耕层断面示意图。

图2 耕作带耕层断面示意图Fig.2 Schematic diagram of plowing zone

2 螺旋带状整地装置功耗分析

根据螺旋带状整地装置工作原理可知：螺旋带状整地装置作业时功率消耗主要来自切土功耗和抛土功耗。

2.1 螺旋带状整地装置运动模型

建立螺旋带状整地装置运动坐标系。坐标系原点固定在搅龙末端旋转轴中心位置，x轴沿搅龙旋转轴斜向上，y轴、z轴分别与x轴垂直且位于搅龙旋转平面上。

设机具前进速度为V，作业时间为t，则位于搅龙螺旋叶片点运动方程为：

式中，V-机具前进速度（m.s-1）；θ-螺旋搅龙入土角度（°）；ω-螺旋搅龙旋转角速度（rad.s-1）；R-螺旋搅龙叶片半径（m）。

利用Matlab画出螺旋带状整地装置运动轨迹，如图3所示。

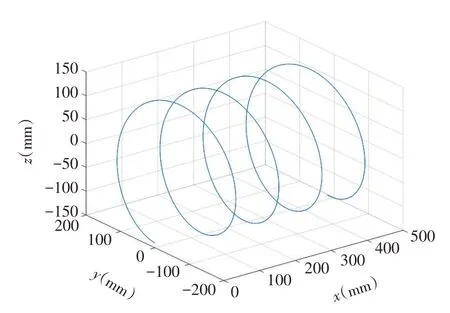
图3 螺旋叶片边缘处点部分轨迹Fig.3 Partial trajectories of the pointsat theedge of the spiral blade

对方程式（1）中时间求导，可得螺线搅龙叶片端点速度在坐标轴上投影：

则螺旋搅龙叶片端点绝对速度的模为：

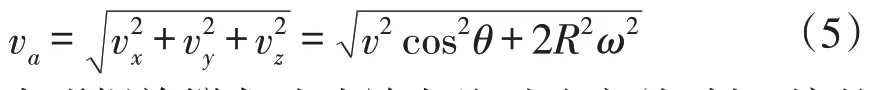
表明螺旋搅龙叶片端点绝对速度（切削土壤的速度）受螺旋转速、作业速度、入土角度及螺旋叶片直径影响。

2.2 切土功耗

土壤强度破坏机理为剪切破坏，在土体内某一截面上，其剪应力等于该截面抗剪强度时，则在该截面上发生剪切破坏[15]。螺旋带状整地装置工作时，在螺旋叶片前方土壤由于受螺旋叶片旋转挤压作用发生破坏，取螺旋刃面微元体ds（见图4），若忽略叶片摩擦作用对土壤应力状态影响，则最大主应力可由应力极限圆求出：

图4 螺旋叶片微元受力Fig.4 Forceacting on micro elements of helical blades

式中，C-土壤内聚力系数（N.m-2）；φ为土壤内摩擦角（°）。

作用在螺旋叶片微元上法向力F1为：

式中，i-螺旋叶片每转在进给方向上位移量（m）；n为螺旋叶片转速（r.min-1）。

作用在螺旋叶片微元上摩擦力F2为：

式中，μ-土壤与螺旋叶片摩擦系数。

参与切削土壤螺旋叶片长度为：

式中，h-作业耕深（m）。

力F1和F2对刀轴力矩为：

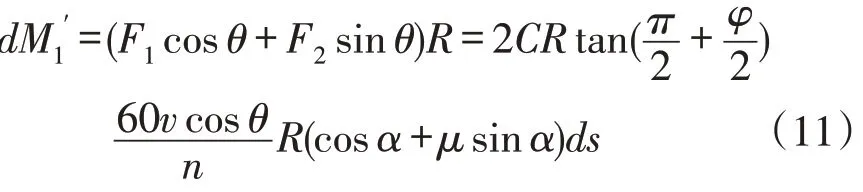
螺旋叶片切削土壤阻力矩为：

由于螺旋叶片切削土壤时仅有半周参与，所以实际切削土壤时力矩为[16]：

螺旋叶片切削土壤阻力矩为：

综上，螺旋带状整地装置切土功耗为：

2.3 抛土功耗

螺旋带状整地装置作业时，会在正前方切削出半圆柱形沟壁（见图1）。切削形成的沟壁可看作倾斜放置的螺旋输送器管壁，故沟壁与螺旋带状整地装置可组成倾斜放置的螺旋升运器，输送方向沿螺旋轴向下。因此，螺旋叶片转速直接影响螺旋叶片上土壤运动状态。当螺旋叶片转速小于临界转速ns时，螺旋叶片仅对土壤有推土作用；当螺旋叶片转速大于临界转速ns时，螺旋叶片开始对土壤产生抛土作用[17]。临界转速可由以下经验公式求出：

式中，A-物料综合特性系数，查文献[18]取50；D-螺旋直径（mm）。

切削后螺旋滚筒内土壤可随螺旋叶片以角速度ω作圆周运动，也可与螺旋叶片产生相对滑动。当土壤颗粒滑动至螺旋叶片边缘时，土壤颗粒速度最大，此时土壤颗粒最大速度为[19]：

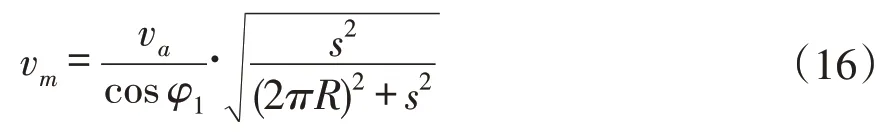
式中，Va-螺旋叶片边缘处绝对速度（m.s-1）；φ1-叶片与土壤摩擦角（°）；S-螺旋叶片螺距（m）。

单位时间内螺旋带状整地装置切削土壤质量为：

式中，ρ-土壤密度（kg.m-3）；L-耕宽（m）；h-耕深（m）。

被抛土壤颗粒动能为：

综上，单位时间内抛土功耗为：

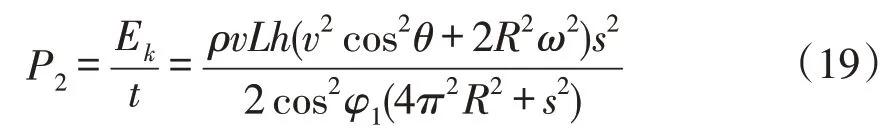
由此，螺旋带状整地装置作业功耗为：

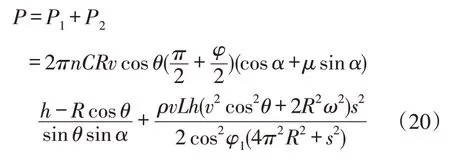
3 仿真试验与分析

为研究螺旋带状整地装置作业功耗和土壤扰动性能，控制无关变量一致性，采用离散元分析软件建立仿真土壤模型，结合正交试验作离散元仿真。

3.1 离散元模型建立

为准确模拟东北壤土物理特性，保证仿真结果可靠性，选取哈尔滨市农业科学院示范园区（位于哈尔滨市万宝镇）试验地东北壤土开展参数测量。2020年9月25日实测0～200 mm深度土层平均含水率21.44%，平均土壤容重1.21 g.cm-3，平均土壤坚实度2.88 kPa。根据东北壤土特点，设置土壤颗粒间力学关系模型为Herts-Mindlin with Bonding接触模型[20]。通过确定仿真接触模型及参数，在不影响装置仿真结果条件下，为减少软件运行时间，建立适用于螺旋带状整地装置离散元虚拟土槽[1 000 mm（长）×400 mm（宽）×300 mm（高）]，土壤密度1 210 kg.m-3。土壤颗粒为单颗球状颗粒，半径7 mm。为模拟土壤颗粒在螺旋带状整地装置作业过程中运动行为，应用Solidworks 2018软件创建出螺旋带状整地装置几何仿真模型，并将几何模型以.stl文件格式导入EDEM中，虚拟土槽和几何仿真模型如图5所示。接触参数设置如下：土壤泊松比为0.25，土壤剪切模量为1×106Pa，土壤-土壤恢复系数为0.13，土壤-土壤动摩擦因数为0.27，土壤-土壤静摩擦因数为0.56，土壤-装置恢复系数为0.16，土壤-装置动摩擦因数为0.35，土壤-装置静摩擦因数为0.6，土壤颗粒间法向接触刚度为3.4×108N.m-1，土壤颗粒间切向接触刚度为1.5×108N.m-1，土壤颗粒间临界法向应力为2×105Pa，土壤颗粒间临界切向应力为6.8×104Pa。

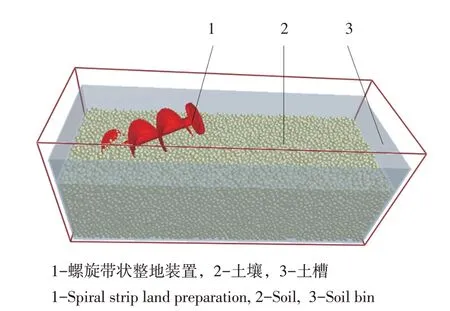
图5 虚拟土槽和几何模型Fig.5 Simulation soil bin and gemetric model

3.2 仿真试验方法

公式（20）功耗模型可知，当土壤物理和力学性质一定时，螺旋带状整地装置作业功耗与作业速度、螺旋叶片转速、入土角度等因素有关。故选取入土角度θ、作业速度V、刀轴转速n为试验因素，根据中心组合试验（CCD）设计原理，设置因素参数作离散元仿真。其中，耕深为120 mm，试验因素编码如表1所示。

表1 试验因素编码Table 1 Experimental factors codes

选取作业功耗为评价指标。利用EDEM 2018软件后处理模块，提取整地装置在仿真过程中扭矩数据，绘制扭矩变化折线图，输出整地装置在仿真过程中各监测点所需总扭矩值，导入EXCEL中求出所有点平均扭矩。

螺旋带状整地装置作业时总功耗为其转动扭矩所产生功耗，其计算公式为：

式中，P-作业功耗（kW）；M-刀轴扭矩（N.m-1）；n-刀轴转速（r.min-1）。

3.3 仿真结果与分析

3.3.1 仿真结果

仿真试验目的是确定不同影响因素对试验指标影响规律，寻找最佳参数。通过EDEM软件实施试验方案，共23组，试验方案与测定结果如表2所示，其中X1、X2、X3分别为入土角度θ、作业速度V、转速n的编码值。

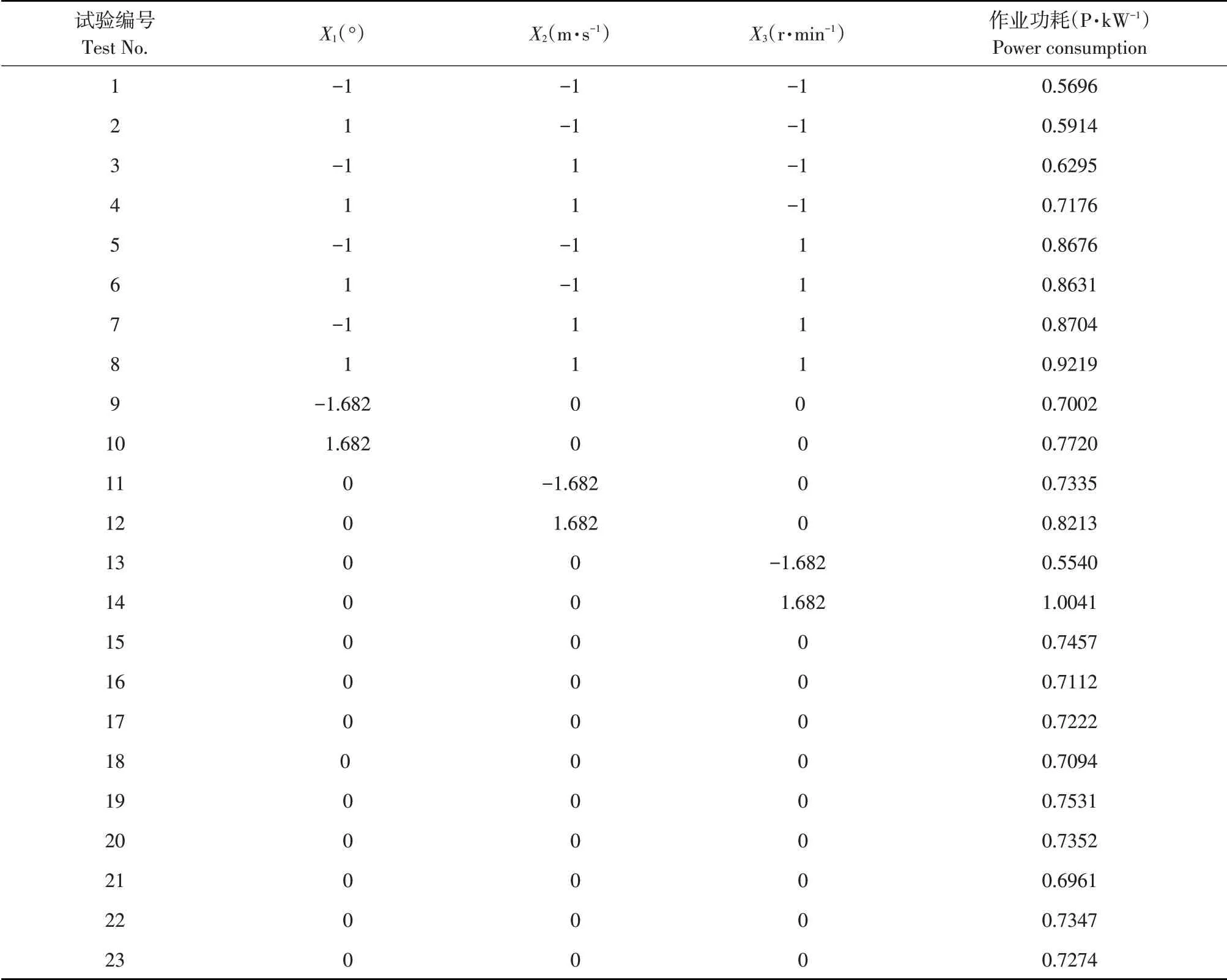
表2 试验方案及结果Table2 Experimental project and results

3.3.2 试验结果分析

为确定实验因素对作业功耗影响规律，应用Design-Expert 8.0.6软件对上述试验结果作回归分析，作业功耗回归方程显著性分析结果见表3。

由方差分析结果可知，入土角度、作业速度、刀轴转速均对作业功耗有极显著影响，且入土角度与作业速度、作业速度与转速间存在交互作用。因素和因素间交互作用对于作业功耗影响顺序为：X2、X3、X1、X32、X22、X2X3、X1X2、X1X3、X12，其中X2、X3、X1、X32、X22影响极显著（P＜0.01），X2X3、X1X2影响显著（0.01≤P＜0.05），其余影响因素均不显著（P＞0.1）。剔除不显著项后，得到作业功耗因素编码回归方程为：

对回归方程（22）作失拟性检验，如表3所示，其中P=0.7973，不显著（P＞0.1），证明不存在其他影响试验指标的主要因素，试验指标和试验因素存在显著二次关系，分析结果合理。

3.3.3 响应曲面分析

通过表3方差分析可知，入土角度X1、作业速度X2、转速X3均对作业功耗P有显著影响，但其交互作用存在不显著项。为研究因素间交互作用对作业功耗影响，利用Design-Expert 8.0.6软件的3DSurface model graphs得出入土角度、作业速度、转速显著交互作用对作业功耗影响的响应曲面，如图6所示。

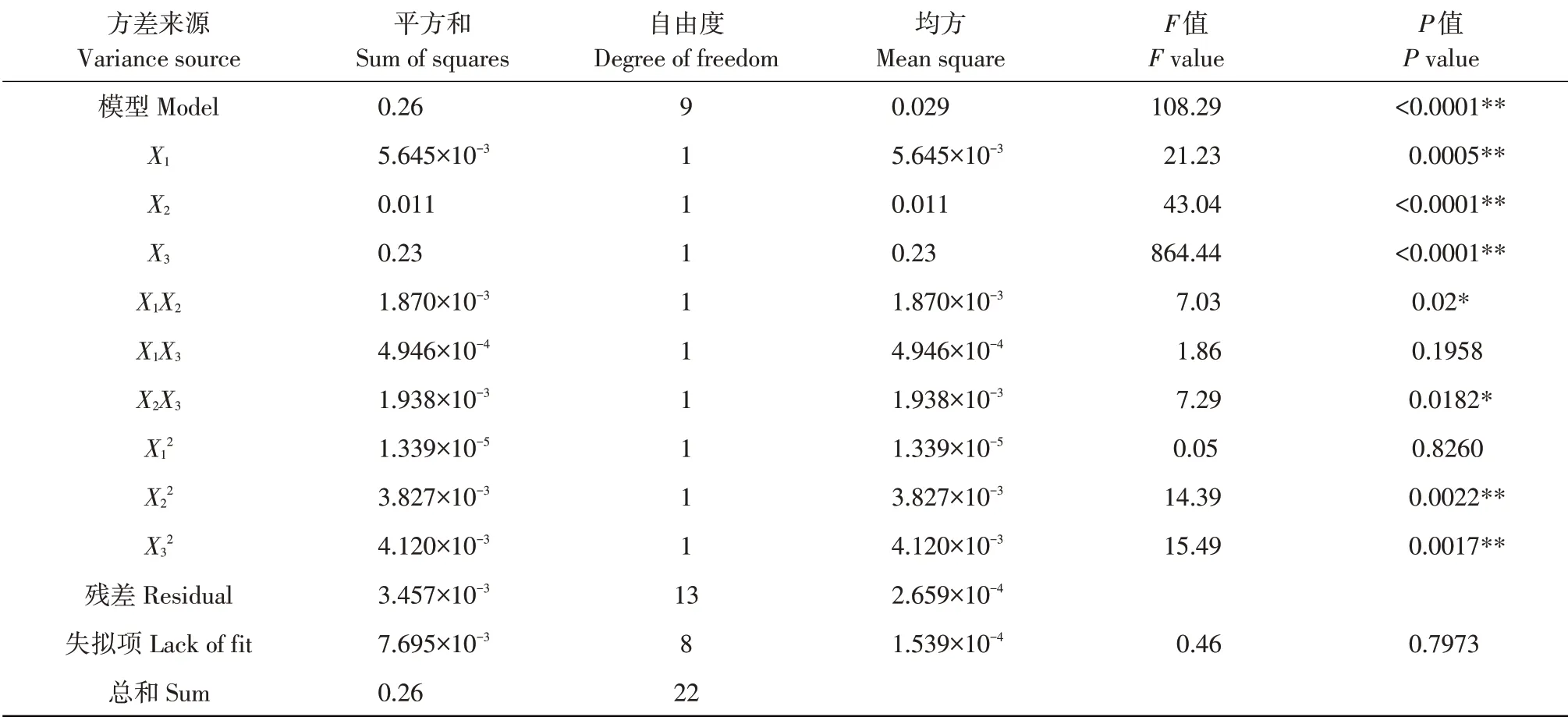
表3 作业功耗方差分析Table 3 Varianceanalysis of power consumption

当螺旋叶片转速为250 r.min-1时，入土角度和作业速度的交互作用如图6a所示：当入土角度一定时，作业功耗随入土角度增大而增大；当入土角度一定时，作业功耗随作业速度增大而增大。当入土角度为25°时，螺旋叶片转速和作业速度的交互作用如图6b所示：当作业速度一定时，作业功耗随螺旋叶片转速提高而增大；当螺旋螺旋叶片转速一定时，作业功耗随作业速度增大而增大。

图6 作业功耗的双因素响应曲面Fig.6 Responsesurface of doubleparametersabout power consumption

3.3.4 参数优化

为得到最佳试验因素水平组合，利用Design-Expert 8.0.6软件中优化模块对回归模型求解，依据螺旋带状整地装置实际工作条件和作业性能要求选择优化约束条件为：

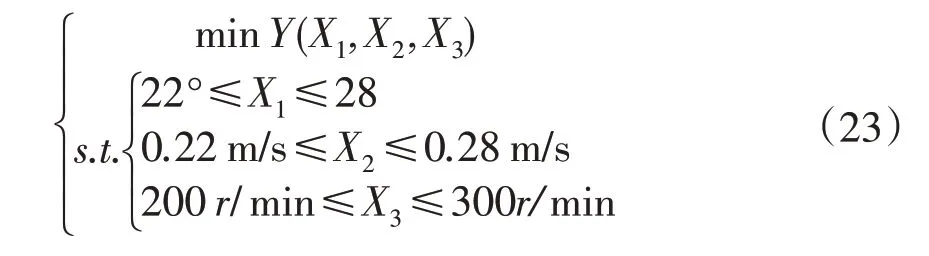
由式（23）可得，当螺旋带状整地装置入土角度为22°、作业速度为0.22 m.s-1、螺旋叶片转速为200 r.min-1时，螺旋带状整地装置作业功耗最小，此时，作业功耗为0.5717 kW，对该优化结果作仿真试验验证其合理性。

4 仿真模型验证

为验证上述离散元仿真模型精度，通过土槽试验台作台架试验，并将实测值与仿真值对比。

4.1 土壤准备

试验于2020年12月在东北农业大学工程实训中心室内土槽试验台进行。试验所用土壤取自哈尔滨市农业科学院示范园区试验田（哈尔滨市万宝镇）。土壤经干燥、筛分后填入土槽，逐层淋水、压实等工序直至土壤容重达1.21 g.cm-3、平均含水率达21.78%（与取土试验田0～200 mm深度所测土壤基本性状保持一致）。每次试验前，将土壤破碎-平整-压实至上述状态，提高土槽试验与田间试验相近度。

4.2 试验原理及装置

试验螺旋带状整地装置作研究对象。室内土槽长×宽×高为6 m×1.2 m×0.4 m，螺旋带状整地装置通过螺栓固定在自制试验台架上，土槽试验台结构见图7。螺旋带状整地装置耕作过程中所受扭矩由HN-50C型动态扭矩测试仪（温州市海宝仪器有限公司）和配套电脑测试软件配合测量与记录。

图7 土槽试验台Fig.7 Soil bin test-bed

试验时，台架固定，土槽前进速度由5.5 kW电机Y132M2-6（浙江方大电机有限公司）和配套变频器控制，变频器频率为120、145、170 Hz时对应前进速度为0.2、0.25、0.3 m.s-1；螺旋带状整地装置转速由YE2-100L（南京环球电机有限公司）和配套变频器控制，变频器频率为14.66、16.66、18.66 Hz时对应螺旋叶片转速为220、250、280 r.min-1；入土角度可通过试验台在10～30°调整，耕深固定为120 mm。利用土槽试验台分别以3种工况开展土槽整地试验，通过扭矩测定软件得到试验过程中扭矩。

4.3 试验结果对比

利用土槽试验台分别以3种工况开展土槽整地试验，通过扭矩测定软件得到试验过程中扭矩值，并利用公式（21）计算出实测功耗值，最后计算仿真值与实测值的相对误差，结果见表4。

根据表4可知，实测值与仿真值相对误差均值为8.34%，范围在7.06%～9.40%；实测功耗值和仿真功耗值变化趋势一致；实测功耗值均大于仿真功耗值，主要是土槽内土壤物理性质不完全一致、作业过程中不可避免的磨擦及磨损、土壤黏附螺旋叶片等原因导致额外功率消耗。误差对比试验结果说明，离散元仿真模型可较准确反映螺旋带状整地装置在作业过程中功率消耗情况，为后续该装置的动力匹配和参数优化等研究提供支持。

表4 误差对比试验设计与结果Table 4 Error contrast test and result

5 结 论

a.基于土壤强度破坏机理，分析螺旋带状整地装置碎土原理，提出该装置切土和抛土过程功耗方程，建立螺旋带状征地装置的整地功耗模型。

b.运用Central Comsite法设计试验，通过离散元仿真模型作模拟试验，并依据试验结果建立整地功耗与入土角度、作业速度、螺旋叶片转速3个试验因素回归数学模型；确定试验因素对试验指标影响顺序为作业速度、螺旋叶片转速、入土角度；同时也确定3个因素对作业功耗影响规律和交互关系。

c.利用土槽试验台测定螺旋带状整地装置在不同工况下作业功耗，并与离散元仿真值对比，得出仿真值与实测值相对误差均值为8.34%，说明该离散元仿真模型可较准确反映螺旋带状整地装置作业功耗。