非线性振动中周期与振幅和能量关系的级数表达式
郝继光,黄亦斌
(1. 南昌市湾里区第一中学,江西 南昌 330004;2. 江西师范大学 物理与通信电子学院,江西 南昌 330022)
通常对振动的处理方式,是将势能函数在极小值点处取到二次项,从而求出振动的频率和周期. 这等价于把该振动视为简谐振动处理. 若想考虑振动频率与振幅的可能关系,在这一阶是不可能得到的,需考虑高阶效应,成为非线性振动问题. 这一关系一直是大家比较感兴趣的问题[1-7],其中针对单摆的研究较多[4-7]. 这一关系一般难以存在有限表达式,故而我们可以就一般情形寻找其级数表达式. 由于计算量较大,我们使用了Mathematica 软件,其中除常见简单命令外,我们还大量使用了Series(幂级数展开)、DSolve(解微分方程),Collect(合并同类项)等命令.
设振子的势能在极小值点(取为x=0,且V(0)=0)附近的泰勒级数为
(1)
上式ω>0.
由能量守恒,有
(2)
将其对时间求导,得
(3)
设正向最远到达x=A处,取此时为初始时刻.兹使用微扰法求其级数解(在数学上类似的例子见参考文献[8]),即设其解为
x=x0+x1+x2+x3+x4+…
(4)
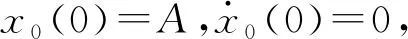
1 精确到二阶的结论
把式(4)代入方程(3),精确到二阶解x2,得方程组:
(5)
于是,使用DSolve命令,精确到二阶的解为
(6)
注意其中有非周期项,而我们的振动显然是周期性的.其原因就在于2π/ω并非真正的周期.可令
ω=Ω+aA+bA2+…
(7)
即Ω为真正的圆频率,其初级近似为ω,高阶部分则表示为A的级数.仅将上式代入式(6)中的三角函数中(其他位置的ω不做替换,因为我们要尽量用原始的系数ω2、k1、k2、…来表示),并利用Series命令展开到A3项,令每一阶的新非周期项的系数为0,即可确定式(7)中的系数a、b.这样得到的T=2π/Ω才是真正的周期.由此可以确定ω、Ω的关系:
(8)
同时式(6)变为
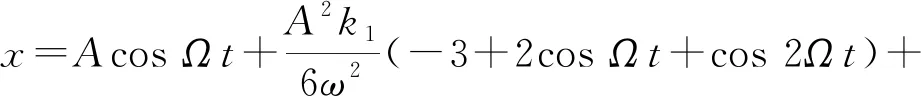
(9)
它恰为式(6)去掉非周期项、并将所有三角函数内的ω换为Ω的结果.另外,由式(9)可以看到,平均位置(坐标的时间平均值,即常数项)为
(10)
设反向振幅为B,即反向最远到达-B处.由于初始条件x=A和x=-B不可区分(或平权),故以上各式若做替换A→-B,则应该保持不变(其中式(6)和式(9)还需重新定义时间零点).这可称为“双向振幅交换不变性”.式(10)的交换不变性给出
(11)
由此得到A和B的相互关系为
(12)
由于式(11)只有两项,所以式(12)也只能保留两项.
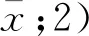
2 精确到四阶的结论
考虑四阶效应时,把式(4)代入方程(3),得到的两个新方程为
(13)
(14)
解x3,x4分别对应A4,A5项,利用DSolve命令可得到结果,但比较冗长,从略.它们中当然也存在非周期项,如x3中的这些项:ωtsinωt,ωtsin 2ωt.为消去各阶非周期项而需做的变换(与式(8)对应)是
(15)
而x3,x4用Ω可表示为
(16)
56064ω4k1k3-5760ω6k4)cosΩt+
1584ω4k1k3+1080ω6k4)cos 5Ωt]
(17)
式(9)、(16)、(17)之和就是方程(3)精确到4阶的解. 容易得到,平均位置为
(18)
由式(15),周期T=2π/Ω为
(19)
此外,由式(2),能量与振幅A的关系为
(20)
以上各式应该都具有“振幅交换不变性”. 具体地,由于E(A)=E(-B),上式可以给出双向振幅B与A的关系为
(21)
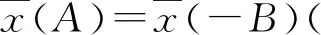
利用InverseSeries 命令反解式(20),得到振幅A与能量的关系:
(22)
其中,能量含在A0中,
(23)
反向振幅B与能量的关系很容易由式(22)得到,只要作替换A→-B,A0→-A0即可,或作替换A→B且把k1,k3,k5、…添负号亦可.把式(22)代入式(19),即可得到周期与能量的关系:
(24)
至于平均位置与能量的关系,可利用式(18)和(22),得到
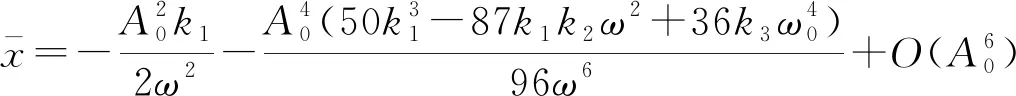
(25)
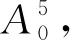
3 例证
例1:单摆
单摆的势能为V(θ)=mgL(1-cosθ).记x=Lθ,将势能展开到x6项,与式(1)对比,得
由前面所说的一般程序,或由式(9)、(16)、(17),得到解为
(26)
其中θ0=A/L为角度θ的振幅.而
(27)
故有
(28)
该结果与其用椭圆积分表示的精确结果展开式的前5阶相同,也与单摆周期的另一级数表达式
(29)
例2:平方反比引力场中的近圆轨道
平方反比引力场中粒子的径向方程为[8]
(30)
其中m1为粒子质量,m2为中心天体质量,常数E和h分别是粒子的总能量和单位质量的角动量,而V(r)为径向运动的等效势能.V(r)存在极小值点r0=h2/Gm2,极小值为-(Gm2)2m1/2h2.r=r0即圆轨道.对于近圆轨道,令r=r0+x,将V(r)展开到x6项,并与式(1)对比,得
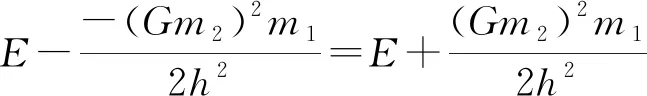
(31)
其中e就是偏心率.于是,式(24)给出周期与能量的关系为
(32)
其中能量含在e中,且用到了r0的定义.式(25)给出平均半径与能量的关系为
(33)
该结果式(32)、(33)是否正确?可以用严格结果检验.平方反比引力场中存在如下关系[9]:
(34)
其中a为半长轴.前者就是开普勒第三定律,后者是用轨道参数表达的能量.两式消去a,将其中的E用e表示,并利用ω的定义,可得
(35)
其级数展开正是式(32).另一方面,对平方反比引力场中的粒子,有[9]
(36)
前者是轨道方程,后者表示角动量守恒. 由两式可计算半径的时间平均值为
将上面的周期表达式(35)代入,并利用ω,r0的定义,得到平均半径为
(37)
其级数展开正与式(33)相符.
——《势能》

