基于函数型进化算子的铝电解多目标优化
范 倩, 龙 伟, 姚立忠, 李炎炎
(1.四川大学机械工程学院, 成都 610065; 2. 重庆科技学院电气工程学院, 重庆 401331)
1 引 言
大型铝电解生产过程能耗巨大并且电流效率并不理想[1]. 铝电解槽内部包含大量复杂的内部物理化学反应和不可预知的外部干扰, 且大多数槽内参数难以检测和及时调整, 故铝电解决策参数优化是一个多参数、高度非线性且机理模糊的复杂优化问题[2-3]. 在保证铝电解槽平稳运行基础下, 考虑如何提高电流效率和降低直流能耗已成为各大工厂的生产目标. 其难点在于选择适应的优化算法来准确、高效地求解铝电解制造系统工艺模型进而获得工艺决策. 目前, 一些经典优化算法已被用于求解铝电解制造过程中的多目标优化问题. 如:文献[4]融合比例加权系数法和简约梯度法, 文献[5]提出引入拥挤距离排序的多目标细菌觅食算法, 文献[6]提出基于差分进化思想的PSO算法, 以吨铝直流能耗和电流效应作为优化目标求解铝电解制造系统的决策参数. 但上述算法自适应性不足, 选择精英个体的压力过大易导致解集陷入早熟或失衡. 非支配排序遗传算法(NSGA-Ⅱ,multi-objective optimization algorithm)因其解的分布更均匀, 结构易于理解而被视作多目标优化的核心算法之一[7-8]. 但基本NSGA-Ⅱ在解决高维复杂非线性优化问题时仍存在选择压力大, 交叉和变异算子设计的随机性易让优秀解集被破坏等问题. 江岳春等[9]利用基于超平面投影的NSGA-Ⅱ(HP-NSGA-Ⅱ,Hyperplane Projection)提高综合能源多主题化调度模型解集的分布性;耿志强等[10]用普通算术交叉代替SBX交叉使群体拥有更广的多样性. 然而, HP策略只针对三维及以上的高维优化问题, 算术交叉比例系数的不确定性仍有破坏解集的风险.
对于铝电解制造过程优化, 现有研究基本只将吨铝直流能耗和电流转换效率(或CF4)作为优化目标. 因此, 针对此二维复杂优化问题, 本文提出一种基于函数型进化算子并融合拥挤熵排序的NSGA-Ⅱ多目标优化算法(Non-dominated sorting genetic algorithm with Crowding Entropy Sorting based on Functional Evolution Operator, FEONSGA-Ⅱ-CES), 通过计算不同级别Pareto前沿面上种群个体的拥挤熵并进行更新来维护优秀解集的多样性. 为了克服基本选择算子和交叉算子致使NSGA-Ⅱ早熟以及减缓系数随机性带来的不良影响, 本文采用基于迭代次数的新型算术交叉算子和高斯柯西变异算子, 并用四种标准测试函数检验FEONSGA-Ⅱ-CES有效性. 最后, 我们将本文所提算法与三种常用经典算法运用于求解铝电解双目标优化问题进行对比, 得出最优运行指导参数集合.
NSGA-Ⅱ[11-12]相较于NSGA-I的改进在于:(1) 使用快速非支配排序, 使算法复杂度降低;(2) 在Pareto同级判断优劣准则中引入拥挤度概念, 减轻后代选择压力;(3) 采用精英策略, 扩大选择空间, 防止信息丢失, 提高了优化结果的精度.
本文引入基于拥挤熵的排序法缓解选择压力, 避免算法陷入未成熟收敛, 然后在选择和交叉两个进化算子方面做出改进.
本文带入分布熵的概念计算拥挤距离, 再利用拥挤熵排序[13-14]精准反映优秀解周围的分布密度. 我们以图1中个体N为例, 计算其分布熵EN.
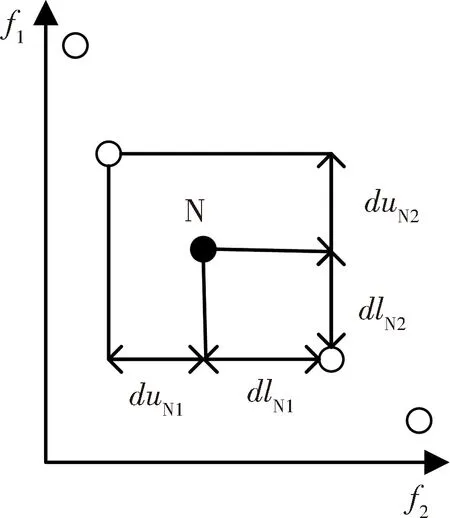
图1 点N拥挤程度示意图
dlij和duij分别代表第i个解在第j个目标函数上与其上下相邻解的距离. 分布熵计算过程如式(2)~式(4).
(2)
cij=dlij+duij
(3)
Eij=-[plijlog2(plij)+puijlog2(puij)]
(4)
按照上述式子计算分布熵后, 对每一目标函数的边界值个体赋予无穷大的拥挤熵值, 保证其始终被选择, 其余个体按式(5)计算其拥挤熵.
(5)
2.2 f(α)函数算数交叉算子
标准NSGA-Ⅱ算法使用的是SBX交叉. 该算子模拟浮点数编码交叉过程, 即随机生成一个阈值, 带入公式按比例线性组合两个父代个体. 本文采用函数型算术交叉算子[10]来取代原有交叉操作, 以确保更广的搜索范围. 其定义公式为:
(6)
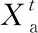
为了提高交叉质量, 我们构造f(α)函数进行动态交叉, 见式(7).
(7)
f(α)为区间[0,1]上的一个值, 保证搜索范围覆盖决策变量的所有领域, 同时交叉比例随着迭代次数增加而规律性地变化, 见图2. 设α=t/β, 其中t为当前迭代次数,β=T/10,T为最大迭代次数. 由此我们得到新的交叉策略如式(8)所示.
(8)

图2 f(α)函数曲线Fig.2 f(α) function curve
图3显示了交叉策略本质过程, 值得一提的是,本文将算数交叉中的α比例系数改进为与迭代次数t相关的f(α)函数. 由图2与式(8)可知, 迭代到中期时,t很小, 导致f(α)接近0.5, 每个子代继承父代各一半的基因. 更具多样化的子代增大了得到性能优秀个体的可能性. 随着迭代次数增加,t变大, 导致f(α)逼近0, 父代基因基本不改变. 父代等位基因的少量交换可以增加算法的局部优化能力. 这样既能维持群体多样性, 又能保证在迭代后期群体向全局收敛方向移动且不破坏最优个体.
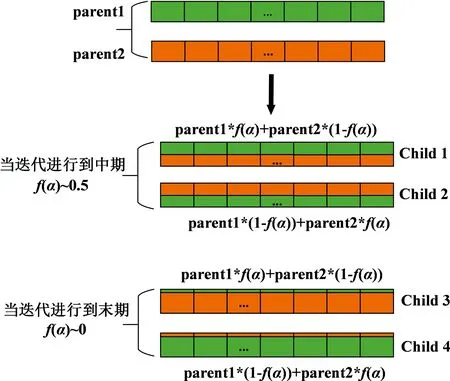
图3 交叉过程示意图Fig.3 Diagram of crossover process
2.3 高斯-柯西变异算子
虽然变异运算只是产生新个体的辅助方法, 但它决定了多目标进化算法的局部搜索能力, 维持优秀前沿解向正确的方向加速收敛[15-16]. 本文采用多点变异, 变异值的随机性会产生较大的无关联扰动, 破坏原有优良基因. 针对上述问题, 我们提出高斯柯西混合变异来增强变异解的质量.
其中,G(x)为高斯分布函数,Cϒ(x)为柯西分布函数,γ为比例系数. 密度分布曲线如图4所示.
由图4可知, 标准高斯分布函数在原点处的峰值较大, 原点两端分布较短. 高斯变异能产生距离原点很近的扰动, 具有较强的局部开发能力. 柯西函数分布特性与高斯相反, 且ϒ值影响曲线特征. 柯西变异能够在当前变异个体附近生成范围更广的扰动, 更容易跳出局部极值. 首先结合两种函数的分布特性引入决策变量柯西变异公式[17-18]:
i=1,2,...,n
(9)
(10)


图4 高斯和柯西函数分布Fig.4 Distributions of Gaussian and Cauchy functions

图5 变异过程示意图Fig.5 Diagram of mutation process
由于柯西函数的自适应γ系数影响曲线峰值及原点两端分布特性, 我们可以调节γ数值来随机改变产生扰动的范围. 由图4可知,γ=0.3, 0.5, 0.7和1.0为差异较大的几个临界点, 故本文设置两个区间. 当种群从0迭代到3/4T,γ在[0.7, 1.0]区间内取值. 图5用Parent1两端基因来表示γ=[0.7, 1.0]时的突变极限范围, 为了直观显示区别, 人为设定区间[0.010, 0.100]. 此区间可以产生较大扰动加强算法的全局搜索性能. 从3/4T迭代到进化结束,γ在[0.3, 0.5]区间选择内取值. 图5用Parent2两端基因来表示γ=[0.3, 0.5]时的突变极限范围, 仍设定区间[0.005, 0.050]. 此区间函数曲线原点的两端分布较短, 产生的扰动较小, 这便于在后期种群趋于稳定时能增加局部搜索能力. 上述T代表最大迭代次数, 具体调节方式如下:
当t: 0~3/4T时,γ∈[0.7, 1.0]; 当t: 3/4T~1T时,γ∈[0.3, 0.5];然后将更新后的γ值带入公式(9).
考虑到增强型NSGA-Ⅱ-CES具有较强的全局搜索能力和较高的搜索精度, 可通过以上三节所提出基于拥挤熵排序法、f(α)函数算数交叉算子和高斯-柯西变异等优化策略提高所求 Pareto 最优解集的分布均匀性. 具体的算法步骤如图6所示.
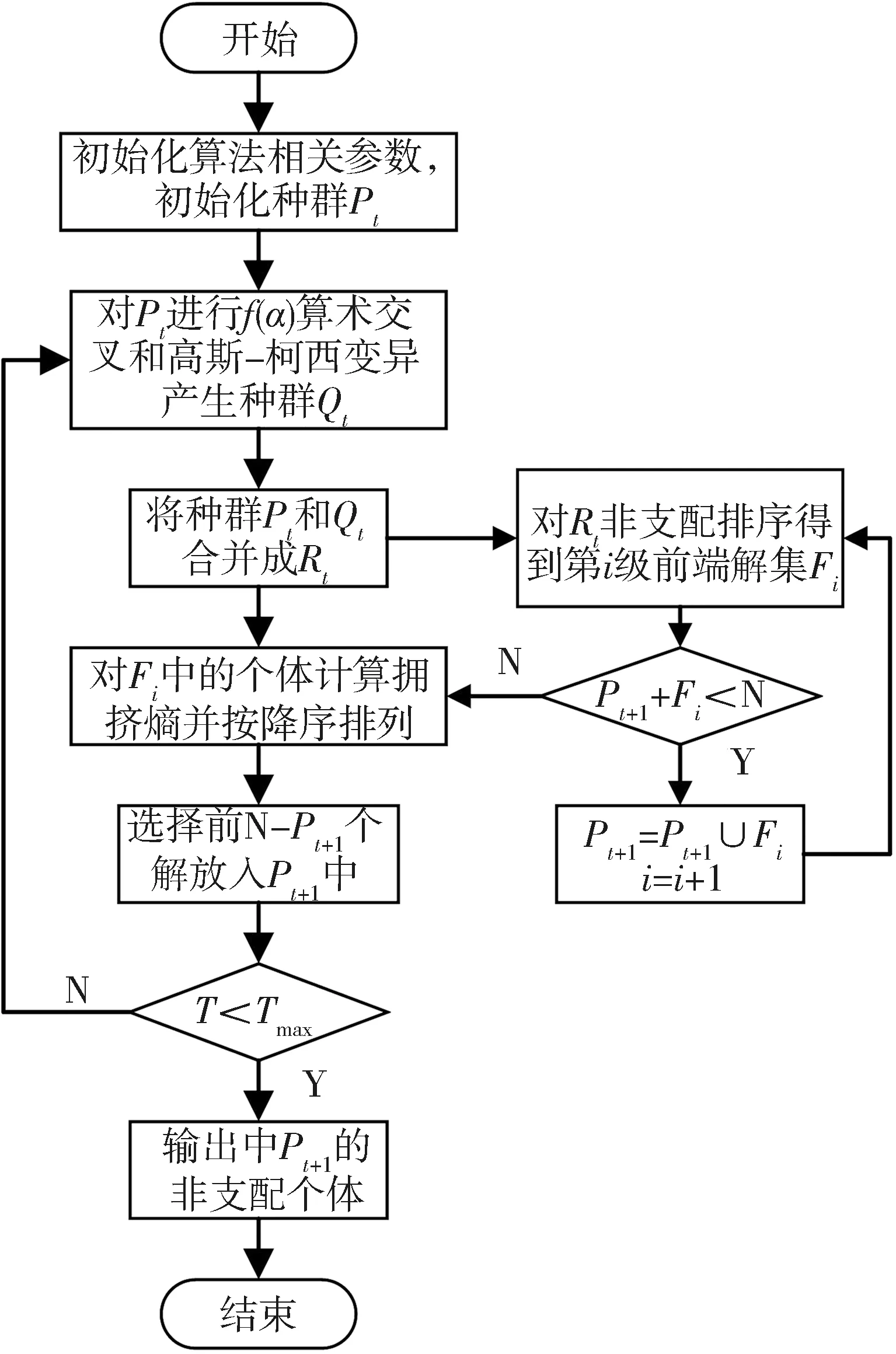
图6 FEONSGA-Ⅱ-CES算法流程Fig.6 Flow of FEONSGA-Ⅱ-CES
为检测算法的可行性, 我们在MATLAB R2020a环境下利用NSGA-Ⅱ、MOPSO、MOEA/D以及本文提出的FEONSGA-Ⅱ-CES求解标准算例函数ZDT1、ZDT2、ZDT3及ZDT6[19]的Pareto前沿解, 用子代空间距离指标(GD)和均匀分布指标(SP)来衡量算法性能[20]. 每个算法均迭代计算300 次, 种群大小设置为 200.
(11)
(12)
其中,P为解集,P*为参考集,d(x,y)表示解集P中的点y到参考集P*中点x的欧氏距离.
图7展示了FEONSGA-Ⅱ-CES求解四种标准函数的Pareto前沿, 其解准确且均匀, 特别是在优化ZDT3时也可以得到拟合度较高的前沿解. 在相同的测试环境下, 对所选的4组测试函数分别独立运行50次, 求其GD和SP的平均值, 见表 1.
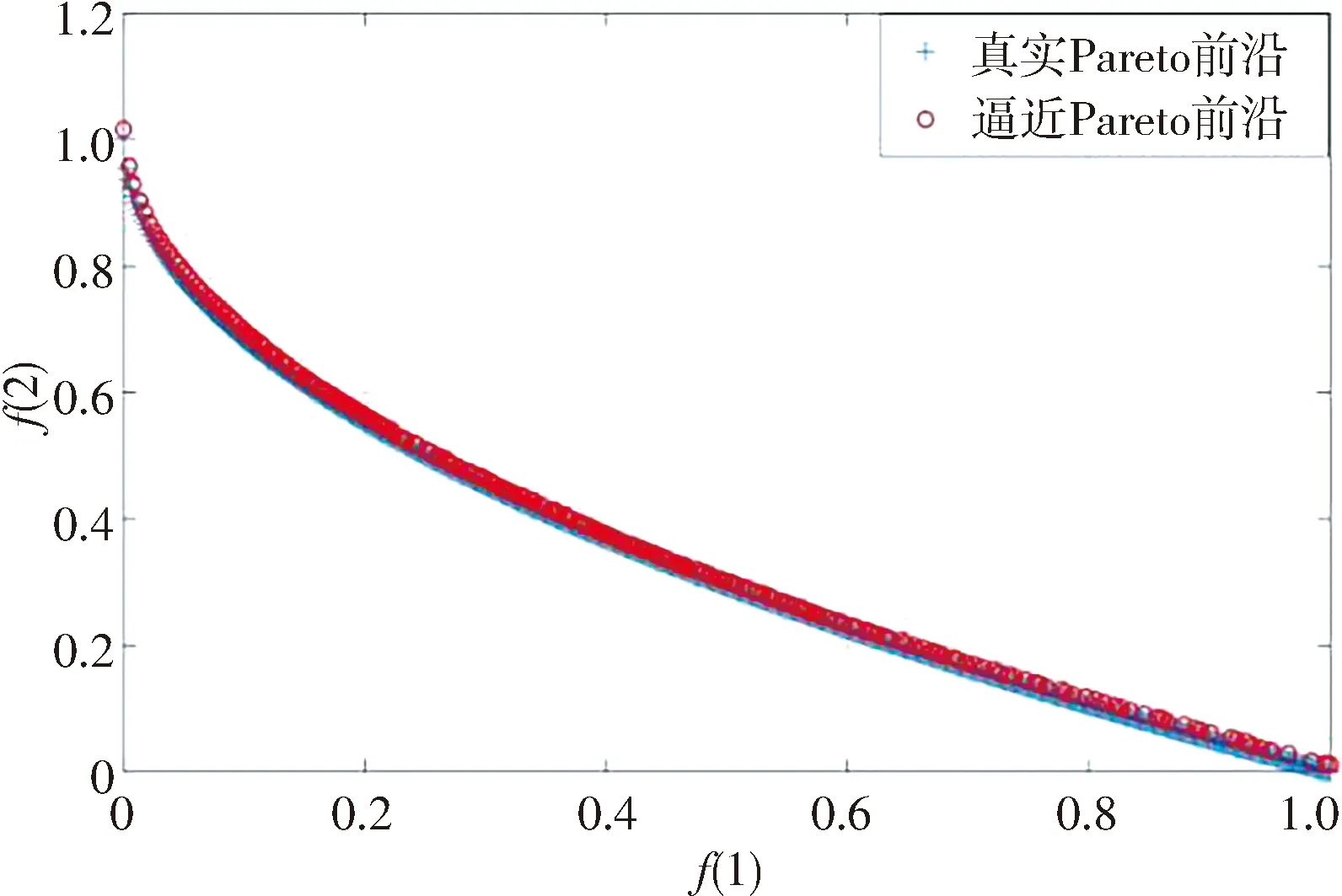
(a) ZDT1

(b) ZDT2

(c) ZDT3
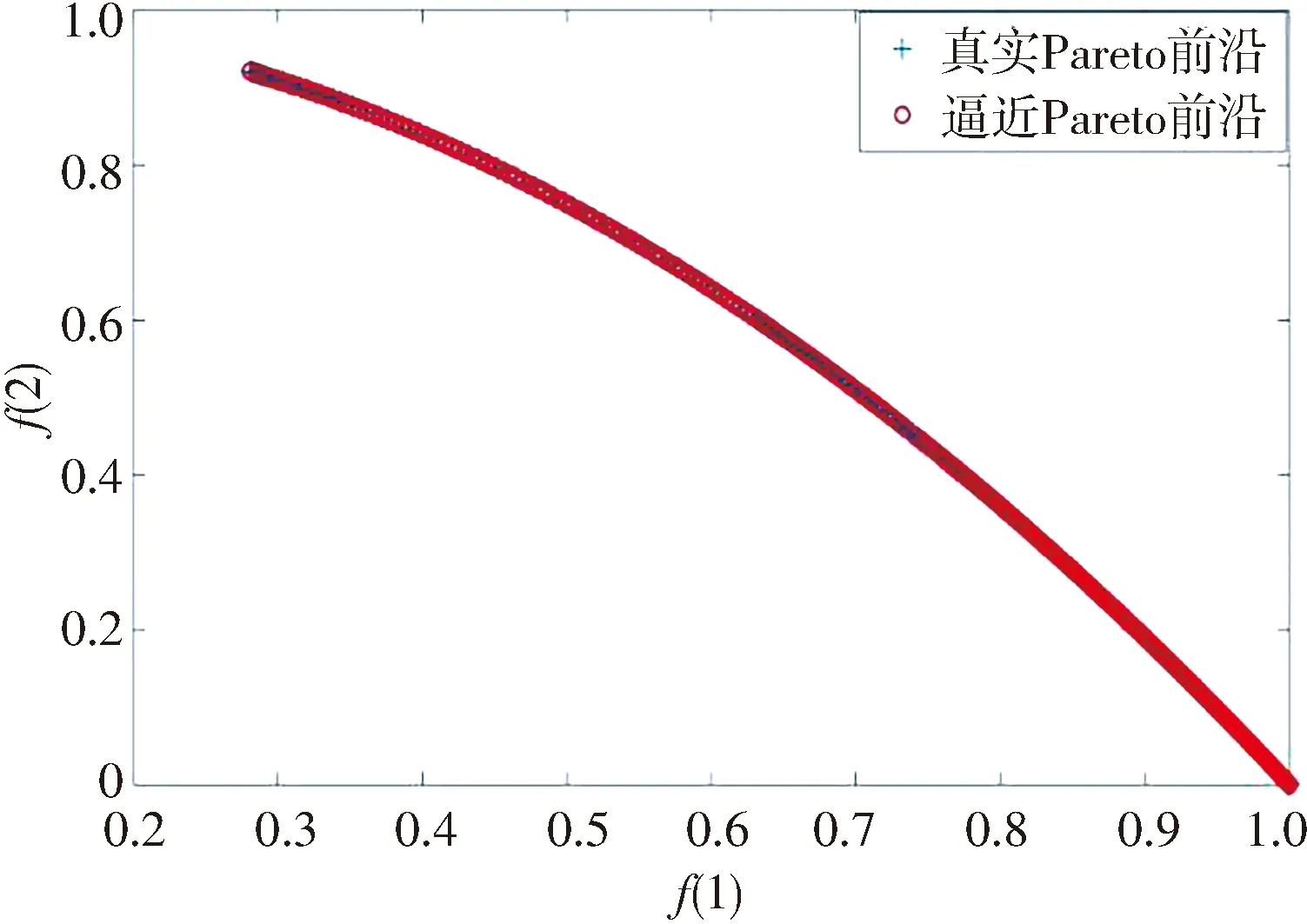
(d) ZDT6
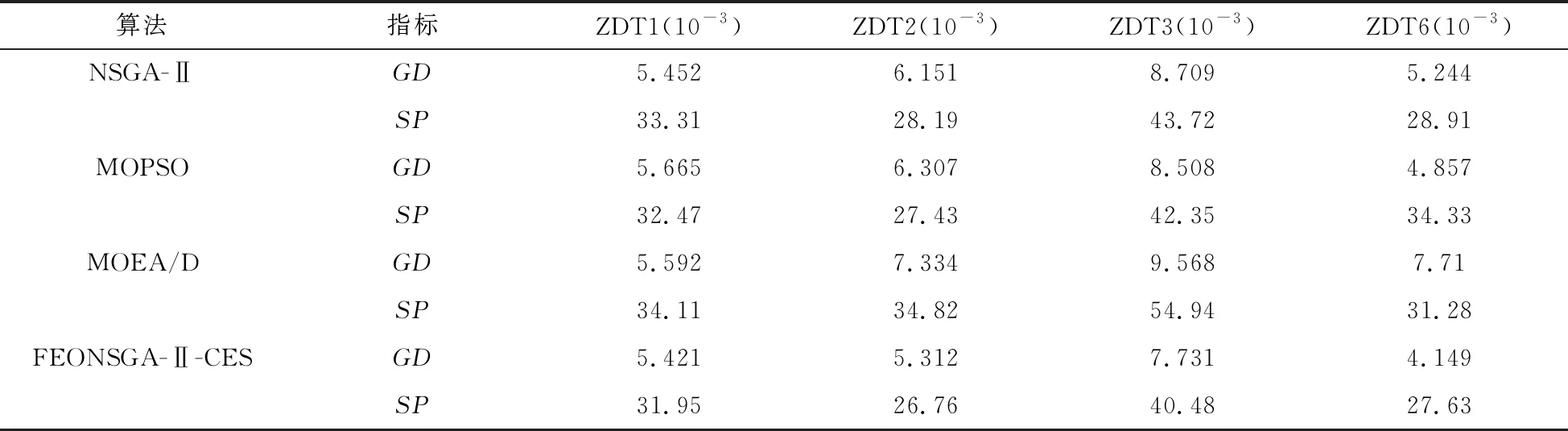
表1 GD和SP测试结果
表1中GD统计结果表明, FEONSGA-Ⅱ-CES由于引入拥挤熵排序且对算术交叉中的比例因子α进行自适应更新, 能更好地克服优化算法本身存在的随机性带来的劣质影响, 随迭代次数改变平衡了算法的收敛性且偏差最小. 根据SP统计结果可知, 在对4个函数进行优化时, 由于高斯柯西混合变异能避免算法陷入局部最优, FEONSGA-Ⅱ-CES能得到更小的SP值. 这表明本文提出的算法能更大程度地保证获得分布更均匀的非支配解, 引导基因群向真实Pareto前沿逼近.
4 铝电解应用实例及仿真结果分析
4.1 多目标优化模型
根据铝电解企业提效减耗的要求, 本文以铝电解直流能耗最小和电流效率最大为优化目标, 通过课题组的预备实验, 总结得到如下主要参数[5]:工作电压U, 系列电流I, 分子比r, 电解温度T, NB次数tNB, 出铝量q, 铝水平ha, 电解质水平he. 具体样本参数见表2.
铝电解直流电耗是指产生一吨铝所需要的直流能耗. 其最小可用数学式表示:DCmin=f1(I,r,tNB,ha,he,T,q,U).
电流效率CE=q/q0×100%,q为电解槽实际铝产量,q0为理论产量. 其最大可用数学式表示:CEmax=f1(I,r,tNB,ha,he,T,q,U).

表2 225号电解槽样本
考虑170kA系列电解槽生产工艺要求, 我们可知:
1 670A≤I≤1 720A,
2.35≤r≤2.60,
3 600mV≤U≤3 750mV,
930℃≤T≤970 ℃,
16cm≤ha≤21cm,
14cm≤he≤18cm,
610≤tNB≤710.
利用GA-WNN神经网络建立铝电解生产过程预测模型克服其高度非线性.GA采用锦标赛选择, 算数交叉和实数离散变异, 设置参数如表3所示.表2中的前200组数据用于建立预测模型, 后23组作为检测样本, 拟合结果如图8所示.

表3 模型的设置参数
铝电解制造系统的目标预测模型精度决定了优化后的Pareto前沿解的可参考性. 图8中用GAWNN模型训练的铝电解能耗最大误差为-0.357%,电流效率最大预测误差为 0.002 7%, 满足建模精度.
采用上述4种算法求解铝电解制造系统中重要参数的一系列Pareto最优解, 取部分结果列于表4. 通过对比表4可知, 当吨铝直流能耗为1.050×104kW·h/t-Al时, 本文提出的优化算法所得电流效率为98.93%, 比其他优化算法优化效果均有不同程度的提高, 比较符合提效减耗的优化目标.
同时取4种算法综合性能较高的一组数据与某铝厂225号电解槽某段时间的实际监测的平均值进行对比, 从图9的仿真结果我们可明显得出与表4一致的结论. 虽然NSGA-Ⅱ优化后的直流能耗略微高于FEONSGA-Ⅱ-CES优化的结果, 但是其电流效率也大幅度低于FEONSGA-Ⅱ-CES的优化结果. 以上的实验结果均表明在相同环境下将函数型的进化算子带入NSGA-Ⅱ提高了该算法的准确性和收敛性.
本文优化结果仅为决策者提供决策范围, 在实际操作中, 人工经验和外部复杂因素[20]必须被考虑. 若要选择决策者满意的解, 需要基于 Pareto 前沿根据决策偏好选择详细的操作条件.
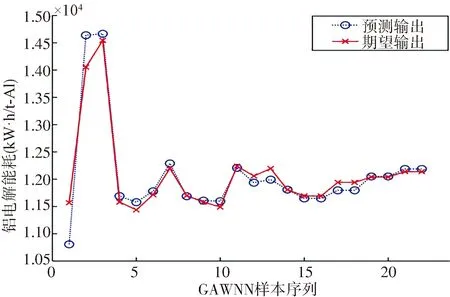
(a) 铝电解能耗预测结果(a) Predicted resultsof energy consumption aluminum electrolytic

(b) 电流效率预测结果(b) Predicted resultsof the CE
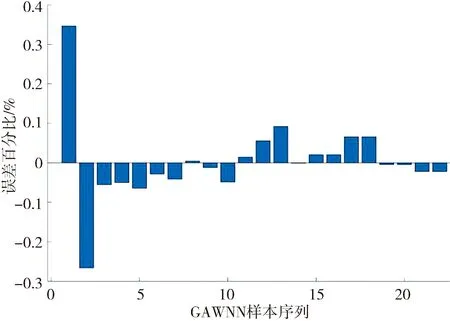
(c) 铝电解能耗误差(c) Energy consumption errors of aluminum electrolysis

(d) 电流效率误差(d) Energy consumption errors of the CE
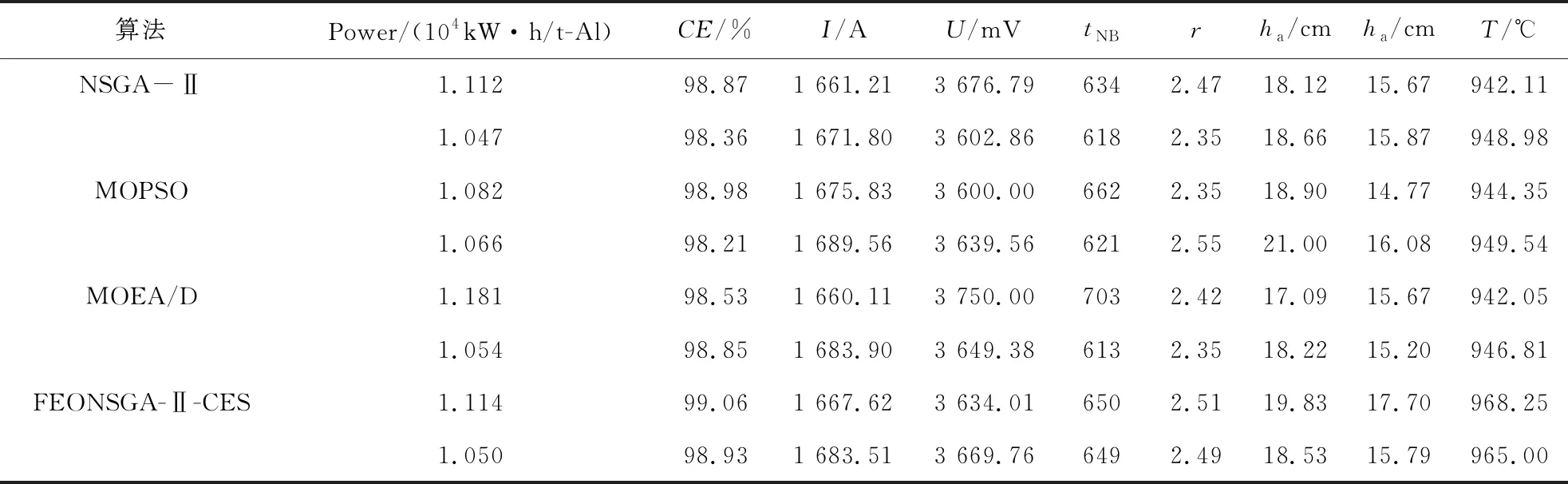
表4 铝电解制造系统部分优秀仿真解

(a) 吨铝直流能耗对比(a) Comparison ofenergy consumption aluminum electrolytic
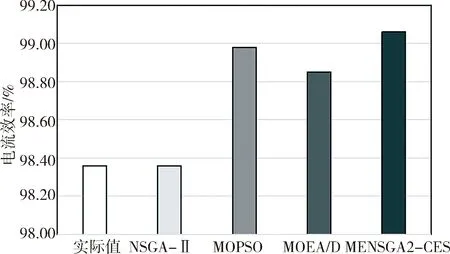
(b) 电流效率对比(b) Comparison of the CE
5 结 论
针对NSGA-Ⅱ在求解复杂铝电解多目标问题时缺乏自适应性而容易导致结果不收敛或解集遭到破坏等问题, 本文提出FEONSGA-Ⅱ-CES增强型算法. 该算法引进了拥挤熵概念,更新子代避免算法陷入早熟;在算术交叉中,采用新型函数交叉算子以防止非支配解遭到破坏;使用随迭代次数变比例系数的高斯柯西变异,扩大搜索区域和提高搜索精度. 通过4组标准算例验证FEONSGA-Ⅱ-CES得到收敛性较好、分布较均匀的Pareto前沿解.
其次, 结合铝电解生产过程特点, 利用GAWNN神经网络建立铝电解生产过程预测模型. 将FEONSGA-Ⅱ-CES 应用到铝电解的多目标优化中, 对比仿真结果表明, FEONSGA-Ⅱ-CES算法求解得到的铝电解槽平稳运行时的决策参数投入到生产中后, 在一定程度上能提高电流效率并降低吨铝直流能耗.
其他因素也影响着得到最终理想的解决方案, 例如废气排放等, 这是我们未来的研究方向.

