基于非线性方程组和优化建模的实验数据重构方法

郝玉洁， 郭子萱， 胡 兵， 唐昌兵， 王浩煜， 辛 勇

(1.四川大学数学学院， 成都 610064； 2.中国核动力研究设计院 核反应堆系统设计技术重点实验室， 成都 610000)

1 引 言

核反应堆的燃耗深度[1]即单位质量核燃料释放的核裂变能量，其中乏燃料(即在反应堆中经受过辐射照射的核燃料)的燃耗深度是衡量核电站经济性和核燃料辐照性能的关键指标.测量乏燃料的燃耗深度可通过测量其释放的γ射线计数[2]来实现.在离散测量γ射线计数过程中，由于受到周围点的干扰，探测器的读数并不精准.这会对后续计算带来误差和困难.为了克服这个问题，有必要通过建立数学模型、运用数学方法来减小这种探测误差，重构实验数据.

在实验数据的去噪处理中,均值滤波算法[3-4]和中值滤波算法[5-7]是常用的两种方法，它们对不同的噪声有不同的去噪特性. 多年来,人们一直致力于改进滤波器,并取得了明显效果,参见文献[5，7].近年来，随着小波理论的发展，很多学者将小波变换应用于信号去噪[8-9].这种方法虽然去噪效果较好，但容易丢失细节信息，导致边缘模糊.最近，邓和刘[10]在形态学噪声滤除器基础上提出了一种基于形态学成分分析(MCA)和K奇异值分析(K-SVD)的去噪方法，可以一定程度上解决边缘模糊问题.

在本文考虑的实验数据重构问题中，误差源于离散探测点之间的相互干扰，不是服从某种随机分布的噪声，因而不能直接应用上述去噪方法，需要建立新的重构模型.本文首先建立了探头扫描数据的正向计算模型，将工程问题转化为求解一种不定的非线性方程组[11].该方程组有无穷多个解，需要建立优化问题[12]形式的重构模型，进而求解其特定意义下的最优解.本文建立了两种重构模型，第一种是根据观测得到的相对误差与参数之间的线性关系构造优化目标函数；第二种根据Lagrange乘子法[13-15]建立重构模型.数值实验结果表明，两种重构模型得到的重构结果都比探测值更接近真实的精确值，相较而言第二种重构模型的重构结果比第一种更加精确，且具有可以直接把探测值作为迭代初值的优点.

本文结构安排如下：我们在第二节中建立实验结果正向计算的矩阵模型；第三节分别基于优化目标函数和Lagrange乘子法建立两种重构模型；第四节通过数值实验对重构效果进行验证；第五节总结本文的工作.

本文考虑的离散测量γ射线计数实验场景如下：被探测物体为一块矩形板，探测器从板的正上方进行散点式的扫描探测.假设有n1行n2列共n=n1×n2个探测点，将第i个探测点的真实值记为xi，此点的探测值记为yi.点的排列顺序如图1所示.

基于离散测量γ射线计数的特点[1-2]，我们对探测实验做以下基本假设：

(i) 探测点行与行之间的距离相同，列与列之间的距离相同，且列距不小于行距;

(ii) 目标点xi周围的探测点会影响目标点的探测值yi，这种影响与两点之间的距离负相关，并且距离相同的点的影响因子是相同的；

(iii) 目标点的探测值yi只受到探测点本身xi和探测点左方xi-1,右方xi+1,上方xi-n2,下方xi+n2,左上方xi-n2-1,右上方xi-n2+1,左下方xi-1+n2,右下方xi+1+n2共9个点的影响，所有9个点的影响因子之和为1.

图1 探测点的顺序Fig.1 The order of detective points

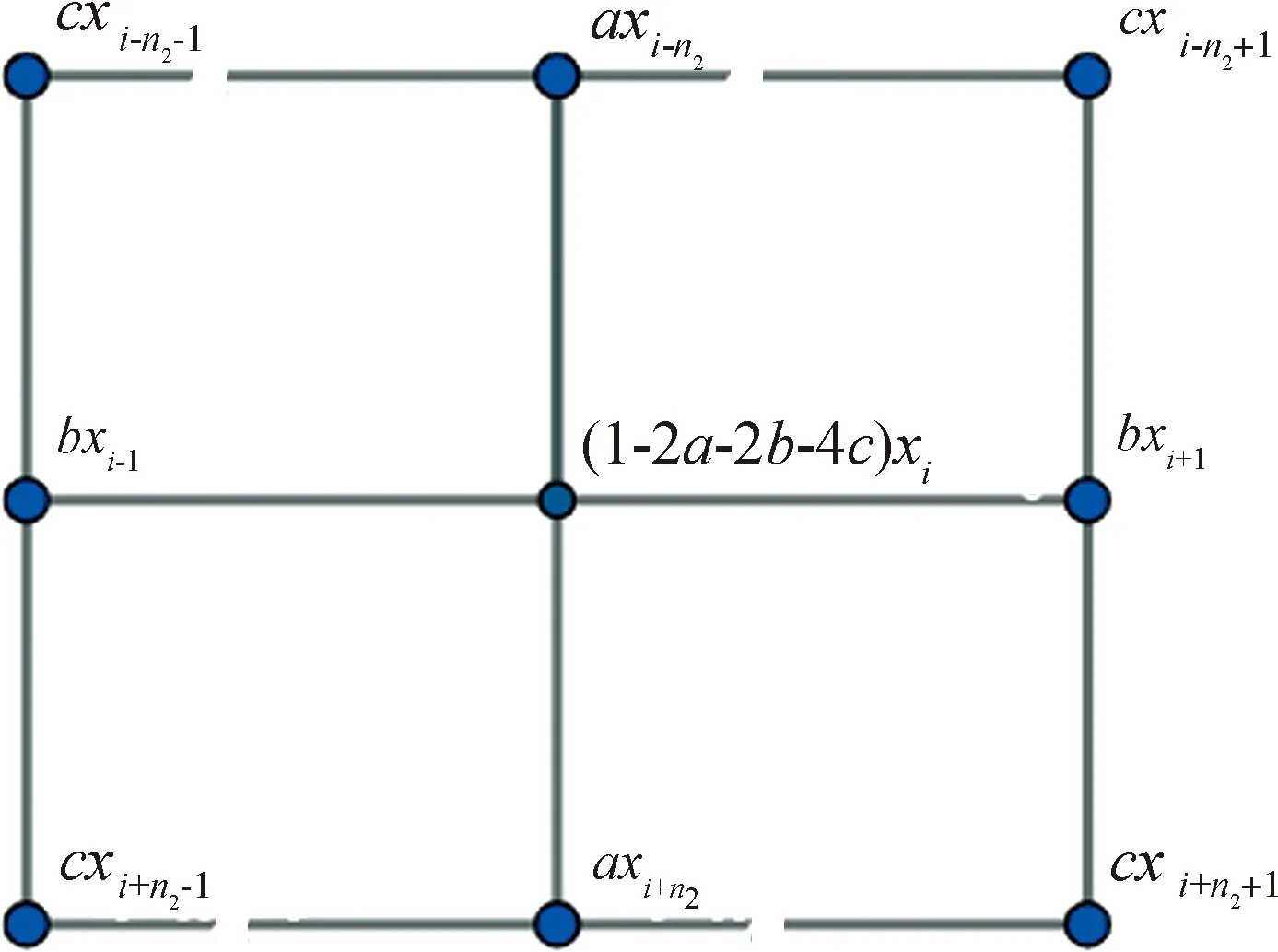
图2 目标点的探测值可以简化为附近9个点(包括该点)的真实值的线性组合

根据以上假设，在探测器扫描目标点xi时，探测值yi受到目标点上下两个点的影响因子是相同的，记为a；探测值受到目标点左右两个点的影响因子是相同的，记为b；探测值受到扫描点左上，左下，右上，右下四个点的影响因子相同，记为c. 则目标扫描点的影响因子为1-2a-2b-4c.探测值yi为附近9个点真实值的线性组合

yi=(1-2a-2b-4c)xi+

a(xi-n2+xi+n2)+b(xi-1+xi+1)+

c(xi-n2-1+xi-n2+1+xi-1+n2+xi+1+n2)

(1)

根据假设(ii),距离目标点越近，影响因子越大，因而参数应满足a≥b>c>0.

记x=(xi)i=1,2,…,n∈Rn是每一个探测点的真实数据组成的列向量，y=(yi)i=1,2,…,n∈Rn是每个探测点的观测数据组成的列向量.我们得到矩阵形式的数学模型

A(a,b,c)x=y

(2)

n阶方阵A可以写成如下n1×n1块的分块三对角稀疏矩阵

其中C和D都是n2阶的三对角稀疏矩阵,

C=a*diag(ones(n2))+

c*diag(ones(n2-1),-1)+

c*diag(ones(n2-1),1),

D=(1-2a-2b-4c)*diag(ones(n2))+

b*diag(ones(n2-1),-1)+

b*diag(ones(n2-1),1).

进一步,对模型矩阵A化简，将其中的未知参数a、b、c分离出来，以使比较清晰地观察A与a、b、c的关系.简单分析后有A=I-(aA1+bA2+cA3)，其中I为n阶单位矩阵，A1、A2、A3为n阶对称正定的矩阵.A1、A3可以写成n1×n1块的分块三对角稀疏矩阵，A2可以写成n1×n1块的分块对角稀疏矩阵，

E=2*diag(ones(n2))-

diag(ones(n2-1),-1)-

diag(ones(n2-1),1),

F=-diag(ones(n2-1),-1)-

diag(ones(n2-1),1).

通过前面建立的矩阵模型，我们已经将这个工程问题转化成如下的数学问题：

Find (x;a,b,c), s.t.A(a,b,c)x=y

(3)

这是一个不定的非线性方程组，有无穷多解. (y;0,0,0)是其中一个解，代表真实值就等于实验值，与实际实验中的相互干扰不符.因此我们需要构建出优化问题形式的重构模型，进而寻找符合实际需求的非(y;0,0,0)的最优解.

3.1 重构模型Ⅰ

由于y=x-(aA1+bA2+cA3)x,则

‖x-y‖2=‖(aA1+bA2+cA3)x‖2，

(4)

图与a2+b2+c2的比值Fig.3 The ratio of and a2+b2+c2

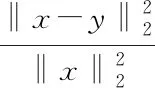
s.t.Ax=y,a≥b>c>0

(5)

在上述模型中，参数k需要事先确定.研究人员可以根据探测场景和自己的经验选取合适的参数值.如果能够利用工程手段得到若干组探测数据y和精确数据x，根据已有的若干组参考数据x和y，用最小二乘法拟合

可以训练得到最优的模型参数k.

利用数据通过最小二乘训练得到参数k时，优化函数在[x;a,b,c]处的取值并不能保证严格为0，但在[y;0,0,0]处是严格为0的，并且为目标函数的一个全局最小值点.所以，如果将[y;0,0,0]作为初值，那么程序并不会迭代.为了克服这个问题，我们考虑给y加上一个小扰动t，即将[y+t;0,0,0]作为初值.

3.2 重构模型Ⅱ

第一种模型的构造思路非常简单直接，但它不能将实验数据[y;0,0,0]直接作为重构模型求解的迭代初值，而我们真正关心的是最终重构结果，a，b，c只是引入的中间变量.为此我们基于Lagrange乘子法建立第二种重构模型.

由于我们只有一个等式约束

x-(aA1+bA2+cA3)x=y

(6)

受Lagrange乘子法的启发，我们可以将其视为KKT条件：

∇xL(x;a,b,c)=

x-y-aA1x-bA2x-cA3x=0

(7)

于是有Lagrange乘子函数

(8)

其中K为常数.对于乘子为a，b，c的拉格朗日乘子函数可以构造很多种优化问题，我们选择如下的最简单形式：

(9)

则根据KKT条件，优化问题(9)的解一定满足式(3).

关于模型参数ki(i=1,2,3)的选取，我们有以下定理.

定理3.1若(x*;a*,b*,c*)是问题(9)的解，且a*,b*,c*均为正数，则

证明 若(x*;a*,b*,c*)是问题(9)的解，则(x*;a*,b*,c*)满足以下KKT条件.

(10)

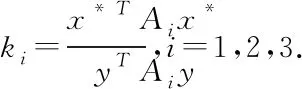
上述定理告诉我们k1，k2，k3的理论选取方式，但由于x*是重构模型需要求解的未知向量，所以这三个参数需要在求解重构模型之前用其他方式选定.类似于重构模型Ⅰ，研究人员可以根据探测场景和自己的经验选取合适的参数ki.如果能够借助工程手段得到若干组探测数据y和精确数据x，我们还可以根据这已有的若干组参考数据x和y，使用最小二乘法拟合xTAix-kiyTAiy=0训练得到模型参数k1，k2，k3.

4 数值算例

本节中我们通过数值实验来检验上述两种重构模型的效果.基于离散测量γ射线计数的一般规律，我们首先按以下方式随机生成50组模拟数据x：矩形板上离散探测点最外一圈的取值位于区间[40，100]，再往内一圈数值位于区间[100，200]，再往内圈数值位于区间[500，600].

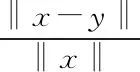
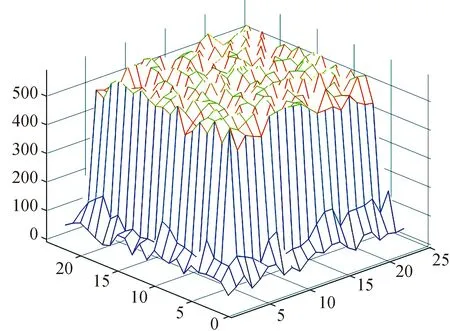
图4 一组x数据的大致形状

图5 两种重构方法的相对误差及其与探测值的相对误差

经过最小二乘训练，得到此次实验中重构模型Ⅰ的参数为k=0.188 826 971,重构模型Ⅱ的参数为k1=1.030 744 286,k2=1.024 777 026，k3=1.025 237 126.重构效果见图5.可以看出，两种重构方法都有效，而第二种重构方法效果比第一种更好.

5 结 论

针对离散测量γ射线计数中的实验数据重构问题，本文建立了探头扫描数据的正向计算模型.通过将工程问题转化为求解一种不定的非线性方程组的数学问题，本文针对此种非线性方程组建立两种优化问题形式的重构模型.数值实验结果表明，两种模型得到的重构结果都比探测器的探测值更接近真实的精确值，相比较而言第二种模型的重构结果比第一种更加精确，且允许直接把探测值作为迭代初值.

在一般的离散扫描实验中，离散探测点之间都存在局部的相互干扰，干扰方式可以被本文的正向计算模型近似.所以本文建立的重构方法，也适用于大多数领域的离散扫描实验数据重构，具有广泛的适用性和工程实用价值.