基于AT的锅炉燃烧温度场重建算法研究
武钰晖, 杨岚斐, 赵 丽, 周新志
(1. 四川大学电子信息学院, 成都 610065; 2. 成都万江港利科技股份有限公司, 成都 610043)
1 引 言
在锅炉运行中,炉膛温度分布直接影响煤粉的燃烧效率以及锅炉燃烧安全,是反映燃烧过程及排放物演变的重要参数[1-2]. 通过了解炉膛温度场,能适时调整燃料的混合比例,使设备处于最佳运行状态;有利于提高燃烧效率,减少污染;有助于检测可能引起爆炸等安全事故的热点,避免燃烧的潜在隐患. 由于锅炉燃烧过程中具有环境恶劣、瞬态变化等特征,传统的接触式测温难以获得准确的炉内温度场[3]. 声学层析成像(Acoustic Tomography, AT)测温技术作为一种非侵入式测温,具有时延小,测量范围大,环境适应能力强等优点[4-6],能够实现锅炉温度场的实时监控,保证燃烧优化运行.
AT温度场重建技术通过测量超声波在待测区域中多条路径上的飞行时间,结合重建算法反演出待测区域的温度分布情况. 常见的重建算法有最小二乘法(Least Square Method, LSM),代数重建法(Algebraic Reconstruction Technique, ART),基于RBF神经网络的方法以及截断奇异值分解法(Truncated Singular Value Decomposition Method, TSVD)等. LSM方法[6-10]是目前广泛用于声学温度场测量的一种典型重建算法,计算过程较为简便,稳定性强,能保证较高重建精度,但是最小二乘法重建出的温度信息数据有限,且重建结果具有边缘缺失效应. ART[1,3,11]的优势在于原理复杂性相对较低,但结果易受噪声干扰. 基于RBF神经网络的方法[12-13]具有任意精度的最优泛函逼近能力,但是需要大量可靠的训练样本来计算合适的参数,实用性受到很大限制. TSVD[14]是将造成解不稳定的较小奇异值直接截去,但是应截断多大的奇异值是一个难题. 在最小二乘法的基础上,颜华等[15]利用Kriging模型同时具有局部和全局的统计特性,在用最小二乘法重建出少量像素后运用克里金法对其进行内插和外推运算,从而得到整个区域的温度描述. Shen等[2]利用多二次插值处理稀疏数据的良好能力,提出一种基于LSM和多二次插值的重构算法,使得重建结果不会在区域边缘丢失信息. Jia等[16]将LSM具有较高稳定性和精度的优点与径向基函数数学拟合的优点综合考虑,研究了一种基于LSM和径向基逼近的改进重构算法,但是径向基函数的形状参数需要数值实验进行合理确定. 因此,如何提高温度场重建精度,改善重建质量依然是一个开放性的问题.
为了提高AT测温重建精度,改善重建质量,本文通过建立基于待测燃烧区域划分单元块的温度描述得到稀疏网格温度场,在此基础上,为了重建出细致的温度场分布,对网格进一步细化,建立细密网格温度场模型,并对重建过程的关键参数进行优化整定,最终实现燃烧温度场的高精度重建.
AT重建温度场的基本原理是超声波在介质中的飞行速度会随介质温度的变化而变化,超声波传播速度与介质温度的平方根呈正比例关系[16],超声速度和气体温度之间的关系可用下式表示
(1)
其中,v表示气体中超声波传播速度,单位:m/s;γ表示气体绝热指数;R表示理想气体普适常数,单位:J/(mol·K);M表示气体的摩尔质量,单位:kg/ mol;T表示气体热力学温度,单位:K.对于确定的气体介质,M、γ和R均为已知量,则P为一固定可知的常数.若介质为空气,P=20.03[16].
当气体介质和超声波传播速度v已知,T表示为
(2)
超声波收发传感器之间的路径长度是固定的已知常数,测定二者间的超声波飞行时间,则可以确定超声波在传播路径上的平均速度.从而取得在待测路径上的平均温度,如下式
(3)
其中,L是超声波收发传感器之间的路径长度;t是传感器之间的超声波飞行时间.
利用超声波对温度场进行重建要在待测区域布置多组超声波收发传感器,选取多条他们之间形成的超声波传播路径,测出超声波的飞行时间,结合合适的温度场重建算法,计算出待测区域的超声波声速分布,最后由声速和温度的关系求得待测区域的温度分布情况.
3 温度场重建算法原理
本文提出的重建算法是一种层层递进的重建算法. 第一层,建立温度场的稀疏网格模型. 将温度场待测区域划分为稀疏的网格,根据超声波飞行时间,采用LSM方法得到待测区域的稀疏网格温度场.第二层,建立温度场的细密网格模型. 在稀疏网格温度信息的基础上,将温度场待测区域进一步细分. 基于最小二乘支持向量机(Least Squares Support Vector Machine, LSSVM)能实现小样本的预测且擅长处理复杂的非线性问题的特点[17],利用训练好的LSSVM建立待测区域细化后网格的温度描述,从而重建出整个待测区域的温度场.第三层,重建过程关键参数的整定. LSSVM重建模型参数会影响温度场重建精度,为了从细密网格温度描述中选出重建精度最高的结果,再利用优化算法对LSSVM模型参数进行整定,从中找出重建精度最高的模型,从而实现温度场的高精度重建(本文提出的算法简称为LLD算法). 其算法思想概括如图1所示.

图1 LLD温度场重建算法思想
3.1 稀疏网格温度矩阵的表征
LLD重建算法重建温度场首先建立稀疏网格,通过LSM方法求解稀疏网格的温度描述. 结合距离公式,声学信号沿着特定的路径从发射传感器到接收传感器之间的飞行时间(Time of flight, TOF)可表示为
(4)
其中,t为超声波飞行时间;v为超声波传播速度;a是超声波速度的倒数;s是超声波传播路径方程.
在温度场重建中,将待测温度场平面划分成N个网格单元块,由于最小二乘法病态矩阵求解特性的限制,划分的单元块数N要小于选取的传播路径数M[2,18].设超声波的传播速度在各单元块内是均匀分布的,根据式(4),超声波在第k条选取路径上对应的超声波飞行时间可以表达为
(5)
其中,ai表示第i个单元块中的超声波平均速度的倒数;ΔSki表示第k条选取路径相应通过的第i个单元块内的长度.

(6)
应用最小二乘法,令下式成立.
(7)
可得到正则方程
ST·S·A=ST·t
(8)
其中,
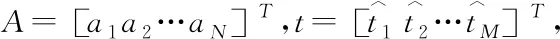
由式(8)可得
A=(STS)-1STt
(9)
根据式(2)可得
(10)
则T=[T1T2…TN]T为N个网格单元块的平均温度组成的矩阵,即得到了稀疏网格中心点的温度信息,也就是作为LSSVM温度采样点的温度.
3.2 最小二乘支持向量机重建模型
在稀疏网格温度信息的基础上,进一步将温度场网格细化,利用LSSVM建立待测区域细密网格的温度描述. LSSVM是一种对标准支持向量机(Support Vector Machine,SVM)的改进算法,相较于SVM,该算法将不等式约束转化为等式约束,采用最小二乘线性系统作为损失函数,将SVM的二次规划问题的求解转化为线性方程组的求解,使得计算进一步简化[17,19-20]. LSSVM方法具有良好的泛化能力,可以实现样本数据较少的预测,且擅长处理复杂的非线性问题. 该方法的基本原理表述如下.

f(x)=ωTφ(x)+b
(11)
其中,ω表示权重向量;φ(·)表示非线性变换映射函数;b表示偏置向量.
则LSSVM的优化问题用下式表示
(12)
其中,J(ω)为优化的目标函数;C为正则化参数,是一个常量;ξi为样本误差向量.
为求解方程(12),引入拉格朗日乘子αi,可将约束最优化问题转化为如下的无约束最优化问题,得到的函数表达式如下:
L(ω,b,ξ,α)=J(ω,ξ)-
(13)
根据Karush-Khun-Tucker(KKT)条件,其最优解满足下式.
(14)
由式(14)则得到求解α和b的线性方程组如下.
(15)
其中,EN=[1;1;…;1]T;α=[α1;α2;…;αN]T;Y=[y1;y2;…;yN]T;IN为单位矩阵;K(xi,xj)为核函数;Ωi,j=φT(xi)·φ(xj)=K(xi,xj).
则最终得到的LSSVM回归函数为
(16)
本文使用径向基核函数,表达式如式(17)所示,其中,σ为核宽度.
(17)
3.3 LSSVM重建模型参数的整定
LSSVM重建模型中正则化参数C和核宽度σ参数取值不同,则重建出的细密网格温度场不同,其精度亦随之不同. 为了进一步提高温度场重建的精度,可以取多组LSSVM模型参数进行预测,得到多个细密网格温度场,从而在得到的细密网格温度描述中选出重建精度最高的一种. 为了在可接受的计算成本内智能地确定,节约人力和时间成本,我们结合优化算法实现LSSVM重建模型参数的整定,从而得到高精度的重建结果. 本文采用差分进化算法对其进行优化. 差分进化算法[22-25](Differential Evolution, DE)是一种基于群体的启发式随机搜索算法,可以通过种群内个体之间的合作与竞争智能产生优化搜索. 相较于其他优化算法,DE算法具有参数少、算法稳定、具有较强的全局寻优能力等优点.
在温度场重建中,重建结果的均方根误差的大小是评判温度场重建效果的好坏的常用指标.因此本文以重建结果的均方根误差作为求适应度的评价指标. 在DE算法中,首先初始化种群规模、最大迭代次数、变异因子、交叉因子等参数,随机生成初始种群,而后对种群进行评价,计算种群内每个个体的适应度. 之后经过变异、交叉和选择,通过不断的迭代计算,保留优胜个体,逐步寻找到最优的参数,从而实现高精度的温度分布重建. 同时,为了提高DE算法的快速收敛性和鲁棒性,在算法的进化过程自动调节变异因子F和交叉因子CR,使得在迭代早期过程中全局搜索能力较强,迭代后期过程中保证计算精度和收敛速度[25],如下式.
(18)
(19)
其中,g是当前进化代数;G是最大进化代数;Fmax、Fmin分别为变异因子最大值和最小值;CRmax、CRmin分别为交叉因子最大值和最小值.
DE算法优化LSSVM参数的具体步骤如下.
(1) 初始化DE的各种参数:种群规模、最大迭代次数、变异因子和交叉因子等.
(2) 随机初始化一个种群.
(3) 对种群进行评价,计算种群内每个个体的适应度. 即分别对每个个体采用LSSVM进行重建,得到每个个体的重建误差,并将其作为各个体的适应度值.
(4) 按照变异策略进行变异操作,按照交叉策略进行交叉操作,得到新的临时种群.
(5) 对临时种群进行评价,计算临时种群中每个个体相应的适应度值;进行选择操作,得到新种群,综合得到适应度最佳的个体.
(6) 判断是否满足迭代次数,若满足输出此时的最优个体即最优解,否则,返回步骤(4).
4 仿真实验与结果分析
4.1 仿真实验与结果
为了评估算法的可行性和有效性,利用LLD算法对东方锅炉厂提供的炉温分布在MATLAB平台上进行重建实验.
温度场待测区域的尺寸为25 m×8.22 m,即锅炉测温区域的实际长度和宽度. 如图2所示,将该区域划分为5×3个网格单元块,其中T1~T10表示均匀布置在待测区域四条边上的10个收发一体的超声波传感器,共形成23条有效的超声波传播路径. 东方锅炉厂提供的三种温度场分布如图3所示,分别为单峰温度场、双峰温度场和高低峰温度场.

图2 超声波收发传感器的布局及待测区域划分情况
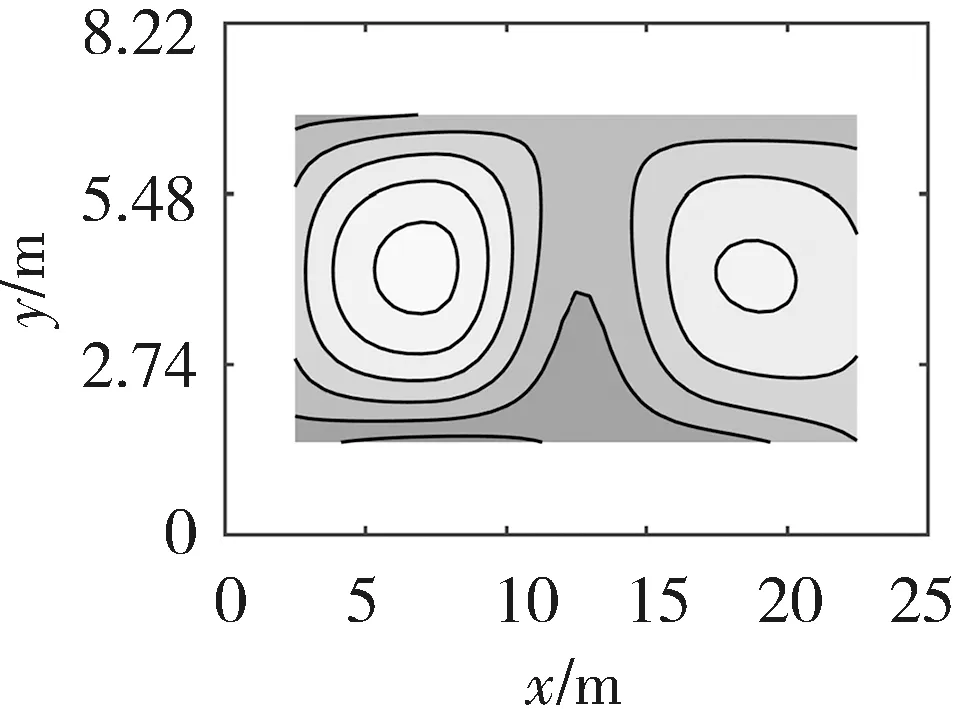
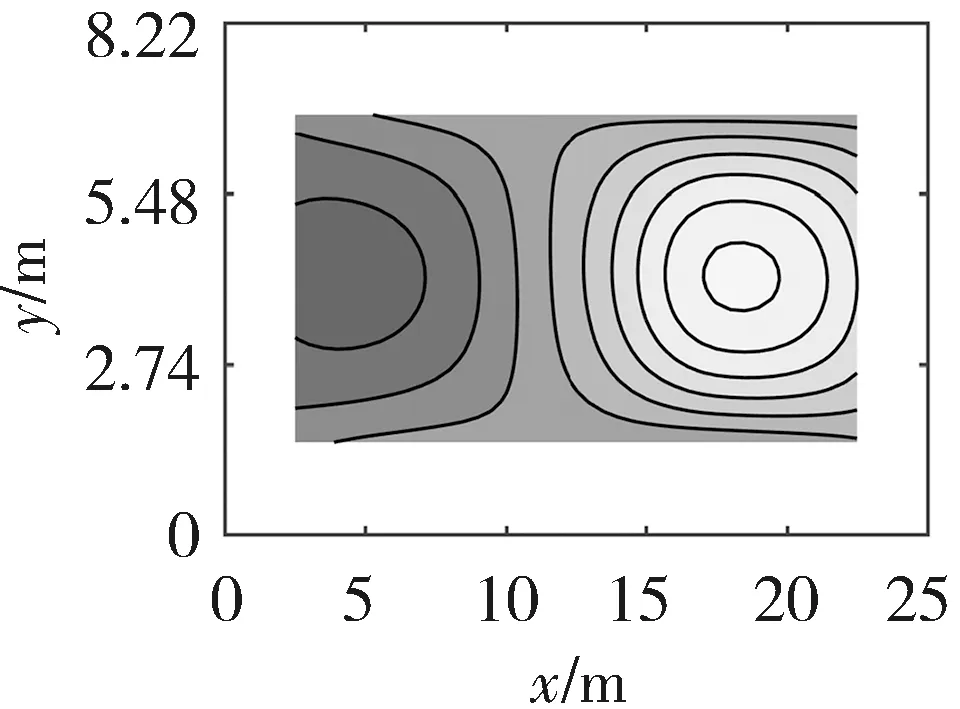
仿真时,DE算法的种群规模设为20,最大迭代次数为200次,变异因子Fmax、Fmin分别为0.9和0.2,交叉因子CRmax、CRmin分别为0.6和0.1,变异策略选用DE/rand/1变异策略,交叉策略选用二项式交叉策略. 将LLD算法重建结果与以下几个算法进行比较:最小二乘法LSM[6],基于最小二乘法和三次样条插值的算法(Algorithm based on LSM and Cubic Spline Interpolation, LSM-SP)[7],基于代数重建法和三次样条插值的算法(Algorithm based on ART and Cubic Spline Interpolation, ART-SP)[3],基于最小二乘法和克里金插值的算法(Algorithm based on LSM and Kriging Interpolation, LSM-KR)[15],基于最小二乘法和多二次插值的算法(Algorithm based on LSM and Multiquadric Radial Basis Function Interpolation, LSM-MQ)[2]. 其中,最小二乘法采用常用的双立方插值(Bicubic Interpolation, BI). 图4~图6分别展示了以不同算法实现的三种温度场重建结果.

(a) 单峰温度场(a) Single-peak temperature field
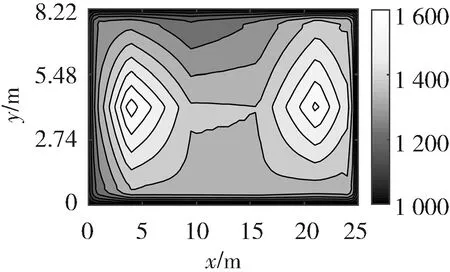
(b) 双峰温度场(b) Double-peak temperature field

(c) 高低峰温度场(c) High-low peak temperature field

(a) LSM-BI

(b) LSM-SP

(c) ART-SP
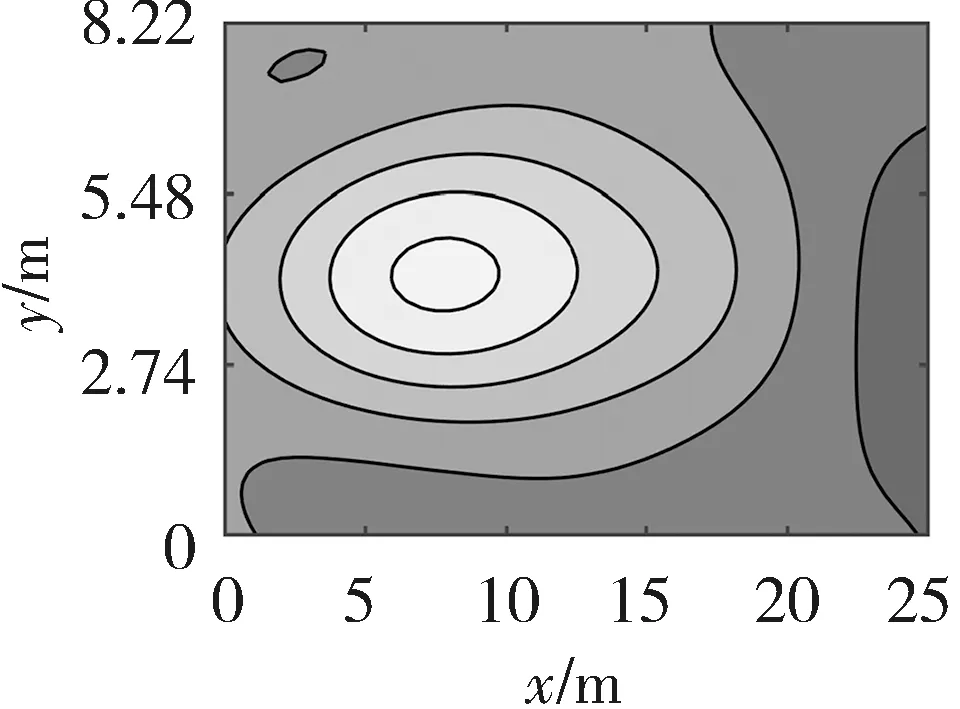
(d) LSM-KR

(e) LSM-MQ
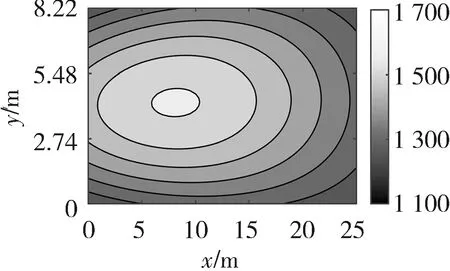
(f) LLD
(a) LSM-BI

(b) LSM-SP

(c) ART-SP

(d) LSM-KR

(e) LSM-MQ
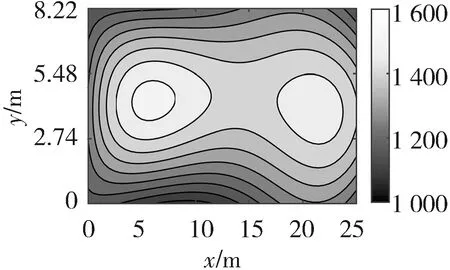
(f) LLD
(a)LSM-BI

(b) LSM-SP

(c) ART-SP
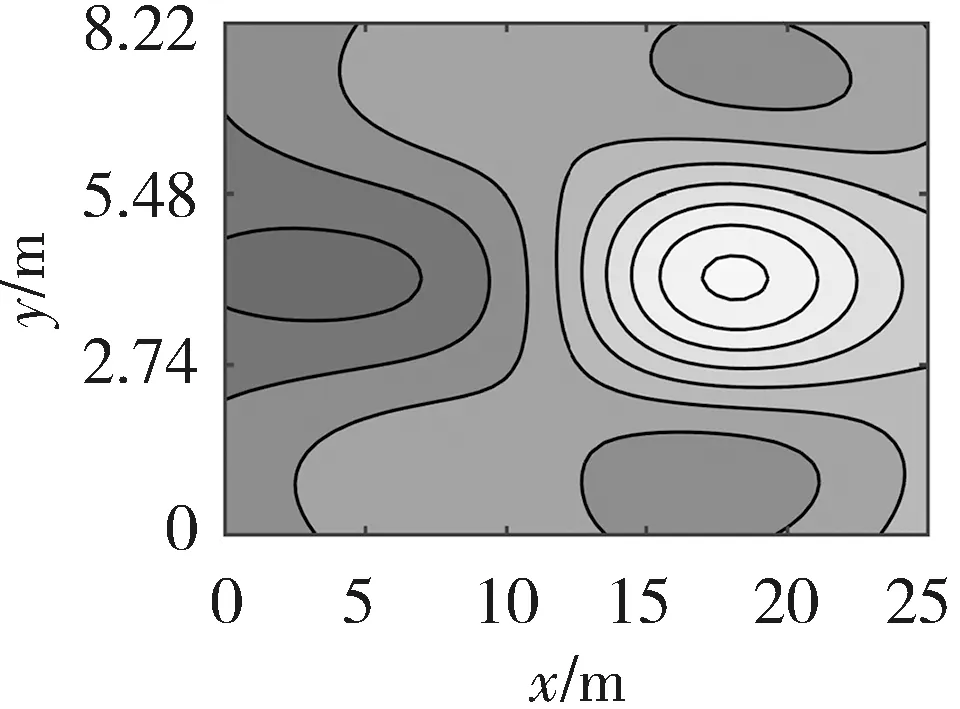
(d) LSM-KR
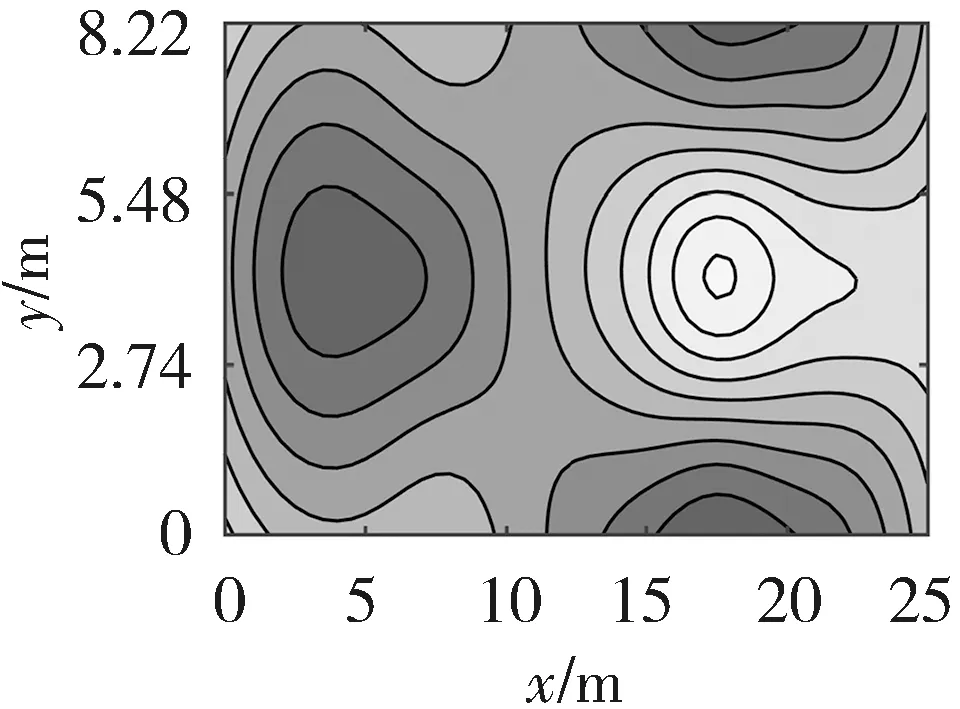
(e) LSM-MQ

(f) LLD
从图4~图6可以看出,LLD算法可以有效地对温度场进行重建. 这6种算法都可以描述温度场的分布信息,但是LSM算法在温度场的边缘存在信息丢失的不足,与另外5种算法相比,LLD算法的温度场重建质量较高.
4.2 误差分析
为了定量评估各种算法的温度场重建效果,本文使用了两种误差评价标准——平均绝对误差以及均方根误差,误差函数定义如下.
(20)
(21)
其中,n为重建出的温度值数目;TRi和TMi分别代表算法所得重建结果与东方锅炉厂提供的模拟温度场在同一坐标下对应的温度值;TMmean为模拟温度场的平均温度.
为了全面分析温度场的重建效果,本文除了从全局分析重建误差外,另外从中心区域和边缘区域两个区域有针对性地对重建误差进行分析对比. 其中,中心区域即最小二乘法和双立方插值能重建出来的部分,边缘区域即待测温度场除中心区域外的部分. 对于LSM-BI算法,由于边缘温度信息缺失,中心区域的误差看作全局误差. 三种温度场重建结果的全局误差、中心区域误差和边缘区域误差如表1~表3所示.
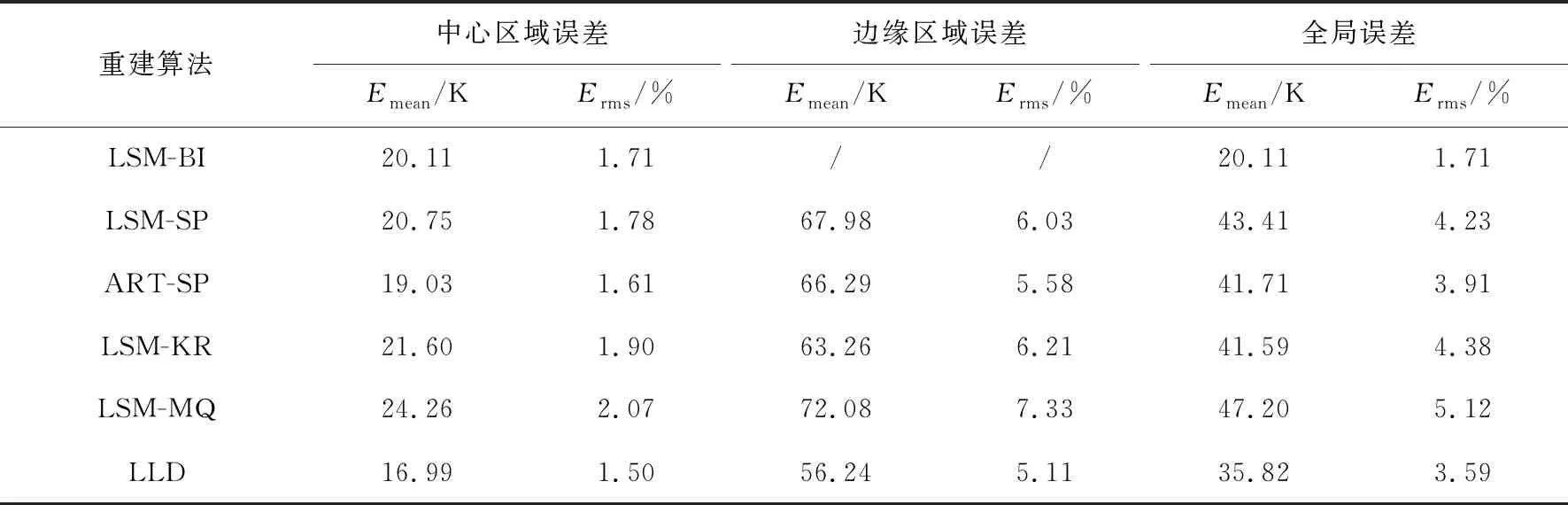
表1 单峰温度场重建误差
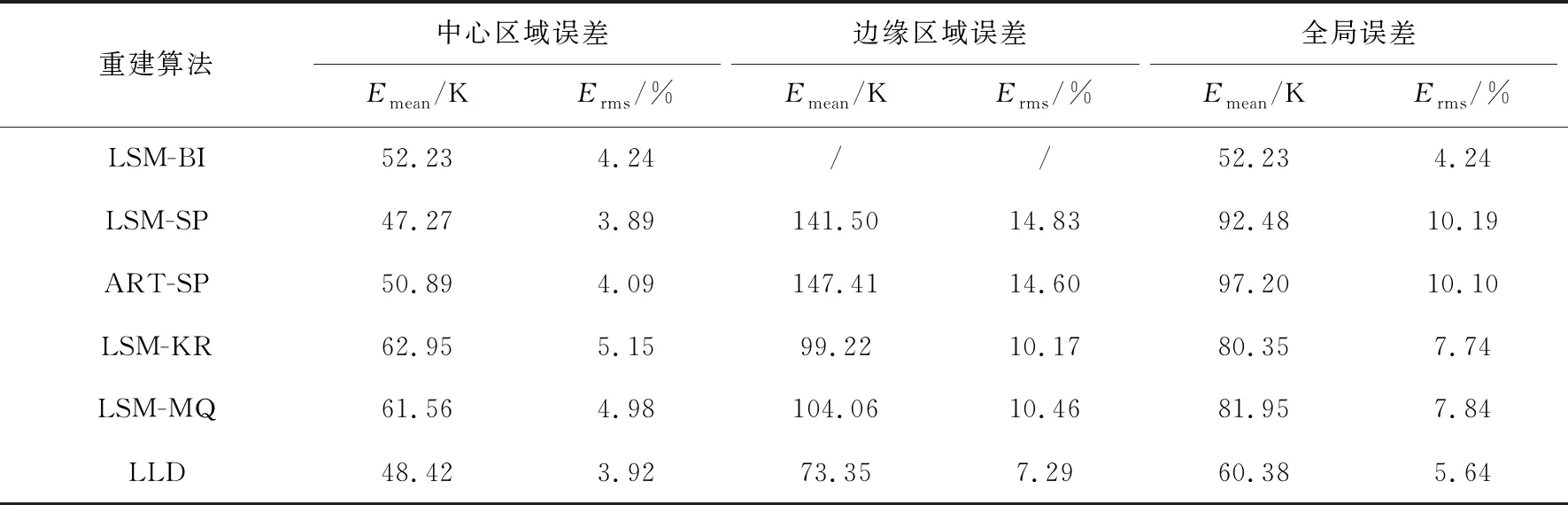
表2 双峰温度场重建误差
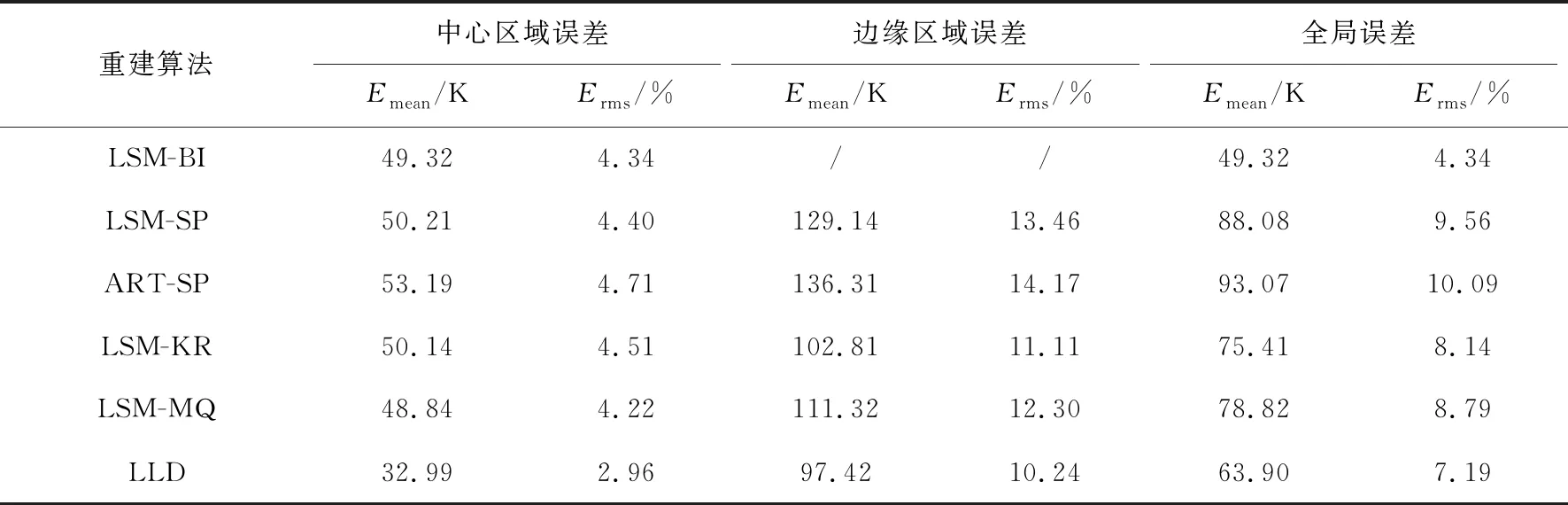
表3 高低峰温度场重建误差
表1表明对于单峰温度场,从中心区域误差和边缘区域误差来看,LLD算法重建结果的平均绝对误差和均方根误差均小于其他比较重建算法. 从全局的误差来看,由于LSM算法的温度场重建具有边缘缺失,故不进入全局误差的对比. 与其他比较算法相比,LLD算法的重建误差最小,重建效果最好. 从表2可以看出,对于双峰温度场,LSM-SP算法和ART-SP算法的重建误差较大. 从全局来看,LLD算法重建结果的均方根误差相较于其他比较算法中的最小值降低了2.1%. 由表3可知,对于高低峰温度场,LLD算法重建结果在中心区域和边缘区域的均方根误差比所有其他算法中的最小值分别降低了1.26%和0.87%. 从全局来看,LLD算法相较于其他比较算法重建精度最高. 从表1~表3的定量分析中可以看出,相较于其他比较算法,LLD算法无论是对于中心区域还是对于边缘区域,都具有较高的重建质量. LLD算法实现了高精度的温度场重建.
4.3 噪声对重建结果的影响
由于超声波飞行时间在实际测量中会存在一定的误差,为模拟实际飞行时间测量值,因此在飞行时间理论值上加入了不同水平的噪声,如下式.
tm=ta×(1+α×Nnoise)
(22)
其中,tm代表测量的超声波飞行时间数据;ta是实际的超声波飞行时间数据;α即代表噪声水平;Nnoise是标准正态分布的高斯噪声. 表4给出了噪声水平分别为1%,3%,5%下的LLD算法重建结果误差.
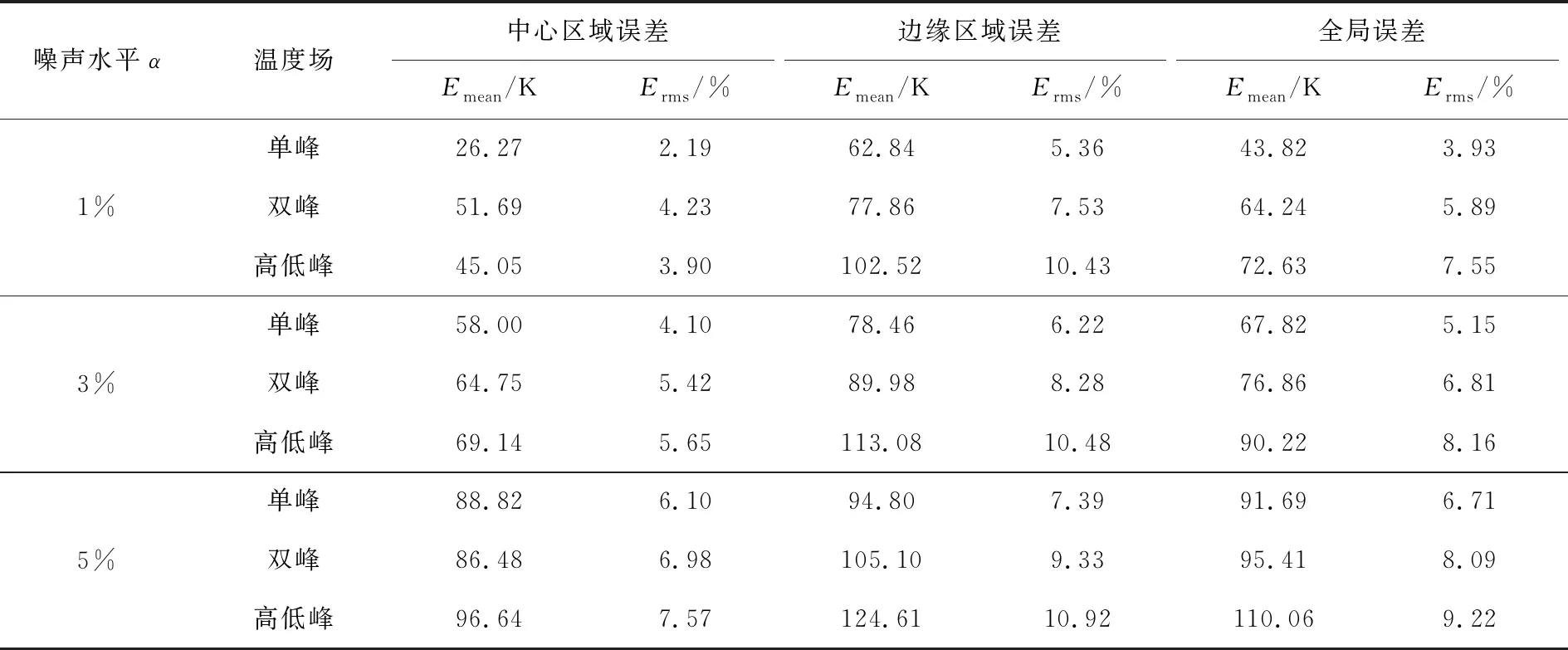
表4 添加噪声后的LLD算法重建误差
表4体现了LLD算法的鲁棒性. 同时可看出,随着噪声水平的增加,温度场重建结果的平均绝对误差和均方根误差也都在逐渐增加. 因此超声波飞行时间的测量精度直接影响温度场重建效果,精度越高,重建效果越好. 这个结果表明,在实际测量时,应当尽量降低噪声干扰,进一步改善超声波飞行时间数据的测量质量.
LLD算法通过对燃烧区域稀疏网格和细密网格温度场的递进重建,以及对LSSVM模型关键参数的优化整定,实现了锅炉燃烧温度场的高精度重建. 通过对锅炉厂提供的三种温度场进行仿真重建实验,证明LLD算法克服了最小二乘法边缘温度信息缺失的问题,能够实现全局重建. 实验结果的误差分析表明,LLD算法的重建误差优于相关算法,它对中心区域和边缘区域的温度场重建都具有较佳的重建性能. 因此,LLD算法能够有效地描述温度场的信息,实现高精度重建. 考虑到噪声水平会影响重建结果的误差,超声波飞行时间数据的去噪将是今后进一步研究的方向.

