求解无约束优化问题的Aitken加速算法
谢亚君 ,姚 洁 ,马昌凤
(1.福州外语外贸学院理工学院,福建福州 350202;2.福建师范大学 数学与信息学院,福建福州 350007)
§1 引言
基于Neculai[1]的工作,本文提出一种求解如下无约束优化问题

的Aitken加速方法,其中f ∈Rn→R为连续可微的函数.
至今为止,无约束优化问题的求解已获得广泛关注,并取得丰硕的研究成果(见[2-6]),其中,包括共轭梯度法(见[7]),牛顿法与拟牛顿法等(见[8-12]).虽然牛顿法具有二阶收敛速度的优势,但是需要计算二阶导数.因此在求解大规模问题时,该方法往往因为计算代价过高而变得不再适用.同时当Hessian阵非正定时,无法保证所产生的方向是目标函数的下降方向.尤其是当Hessian阵奇异时,算法无法继续循环迭代.修正牛顿法可在一定程度上克服此缺陷,然而修正参数的选取较难把握,对收敛速度亦有较大影响.众所周知,拟牛顿法可以避免这些缺点,在迭代过程中不需要计算目标函数的Hessian阵,却在某种意义下具有Hessian阵的作用,因此该方法在相关领域得到广泛的应用.例如,均衡问题,神经网络,激光检测,非线性方程组等(见[13-16]).
假设x0为某个初值点.求解问题(1)的迭代格式有如下表达式

其中αk是由某种线搜索,例如Wolfe或Armijo线搜索获得的步长,dk表示搜索方向.通常对问题(1)的迭代求解格式有两个主要切入点,一个是针对步长因子αk进行合理设计,另一个是考虑有效地选取较优的搜索方向dk.详细可参看文献[17-20].
牛顿法是通过求解如下方程得到牛顿搜索方向dk,

其中Gk,gk分别表示函数f在点xk处的Hessian矩阵和梯度值.鉴于Hessian阵Gk高昂的计算代价,可寻求一个矩阵Bk+1作为Hessian阵Gk+1的一种近似替代.将函数f在点xk+1处利用二次Taylor展开得到近似方程

进而构造所谓的割线方程

其中sk=xk+1−xk,yk=gk+1−gk,Bk+1=Bk+Δk,Δk可视为误差校正矩阵.利用割线方程推导近似Hessian阵Bk+1,关于矩阵Bk+1的有效选取方面已有一系列较好的研究成果.例如,秩1校正公式或BFGS 算法等(见[21-23]).
在文献[1]中,Neculai证明了一个简单而有效的对角拟牛顿更新公式来求解


针对问题(6),基于对角拟牛顿更新迭代法(DNRTR)(见[1]),提出一个修正的Aitken加速迭代格式来求解无约束优化问题(1),该方法在与前者对比的过程中显示了非常良好且具有明显优势的收敛性能.
本文剩余部分组织如下:§2提出求解无约束优化问题(1)的修正Aitken加速迭代方法,同时证明了其具有良好的高阶收敛性能.数值实验和结论分别安排在§3和§4.
§2 算法及收敛性
本节考虑改善对角拟牛顿更新方法(DNRTR)(见[1]),进而引入一个修正Aitken加速迭代格式来求解优化问题(1).最后提供重要的理论证明和收敛性结果.首先注意到问题(6)亦可转化为如下形式

问题(7)的Lagrangian函数为

其中λ表示其Lagrangian乘子.由最优性条件可得

将(10)式代入(7)式,即可得Lagrangian乘子
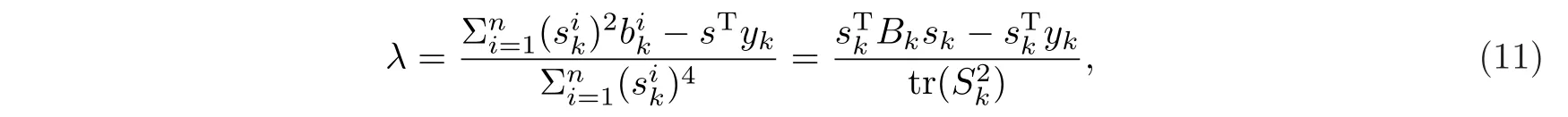

算法1(基于拟牛顿更新的Aitken加速算法(AADQN))
步1 给定初始点x0∈Rn,参数0<β <1,0<σ <0.5,m=0及充分小的正数ε1,ε2>0.计算向量g0=∇f(x0).令d0=−g0,k=0.
步2 若‖g(xk)‖2<ε1停算;否则,转到步3.
步3 计算满足线搜索的步长αk,若不等式

成立,令mk=m,αk=βmk;否则,m:=m+1,然后循环(14).再计算

步4 利用公式(12)更新对角矩阵Bk+1.
步5 令

其中i=1,···,n,.置xk=.
步6 更新搜索方向

步7 置k:=k+1,返回步2.
注记1显然经过计算可知(19)所确定的搜索方向是下降的,即g(xk+1)Tdk+1<0.事实上有

由上式可得,若‖g(xk+1)‖≠0,则有g(xk+1)Tdk+1<0.

当k→∞,若xk→x∗且‖g∗‖→0,则由算法步5定义的格式x=φ(x)即为不动点迭代.关于‖g∗‖→0的事实将在后面收敛性分析给出详细证明.
下面先给出算法的适定性证明.
引理1序列{Δk},{Bk}由更新格式(12)产生.此外,若‖sk‖≠0,且存在(i=1,2,···,n),其中为对角矩阵B0的第i个对角元素,则对所有的正整数k,序列{Δk},{Bk}有界.
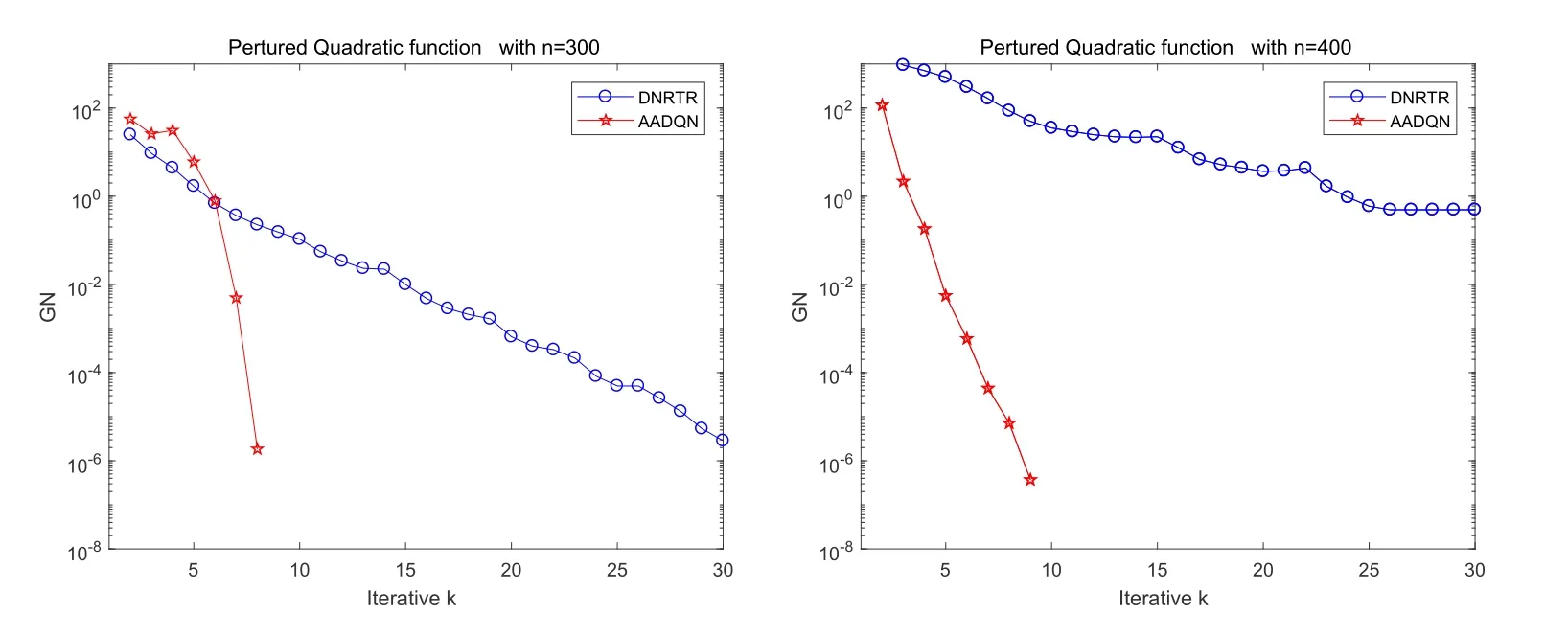
证当k=0,y0=∇2f(ς0)s0,其中x0<ς0 注意到‖s0‖2≤n()2且由已知条件 即B1也是有界的.从而由归纳法可得引理结论. 文献[24]中给出了所谓界退化性质 其中Bk+1是前一步迭代矩阵Bk的更新,νk=max{‖xk+1−x∗‖,‖xk −x∗‖},κ为某个常数.该文描述了Hessian矩阵与其近似矩阵Bk+1可由前一步迭代中二者的差值来控制的事实,既满足界退化性质,同时也给出了满足此性质的算法至少具有q-线性收敛的结果(详见[24]).下面证明更新公式(12)满足界退化性质. 引理2若‖sk‖≠0,则更新公式(12)满足界退化性质. 证由更新公式(12)可得 由于‖sk‖≠0,因此必存在ρ>0,使得‖sk‖>ρ,同时有且 其中˜sk为向量sk的最大值分量.注意到 综合以上引理1-2 可得下面结论. 定理1若存在两个正的常数ε与δ满足不等式‖x0−x∗‖ <ε及‖B0−∇2f(x∗)‖F <δ.那么由更新格式(12)产生的序列{xk}为适定的. 定理2设{xk}是由算法1产生的序列,f(x)有下界且对任意的x0∈Rn,∇f(x)在水平集 上存在且一致连续.则 (a) 下降方向dk满足与−gk的夹角θk的余弦值大于某个常数λ ∈(0,1); (b){xk}的任意聚点x∗都满足∇f(x∗)=0. 证(a) 由(19)式中步长dk的选取可知,若‖gk‖≠0,当(Bk)ii ≥ε2>0(i=1,2,···),则 否则当(Bk)ii ≤0,由算法可知取步长dk=−gk,从而cosθk=1. 综上可知cosθk >λ >0,其中λ ∈(0,1). (b) 用反证法,设x∗是{xk}的聚点且∇f(x∗)≠0.由条件可知f(xk)→f(x∗)且f(xk)−f(xk+1)→0.又由(14)式可得 其中sk=βmkdk.若gk↛0,则由(30)式可知,‖sk‖→0.又由(14)可得,对于,不等式 由于‖pk‖=1,因此{pk}有界,从而存在收敛子列.不失一般性,仍记为{pk}→p∗(‖p∗‖=1). 将(33)两边取极限得 对上式求极限可得 即∇f(x∗)Tp∗<0,与(35)矛盾.因此有∇f(x∗)=0. 下面的定理将说明:在算法1中的步5,借助(20)式中的Aitken迭代格式,将对算法DNRTR[1]执行了有益的改善和加速. 定理3假设算法1(即AADQN)满足引理1-2以及定理2的条件,则由算法产生的序列{xk}收敛于优化问题(1)的解x∗且收敛阶高于算法DNRTR. 证显然由引理1-2以及定理2可知算法1产生的序列{xk}收敛于优化问题(1)的解x∗.由文献[1]可知算法DNRTR至少为q-线性收敛的.下面证明算法AADQN所产生的序列{xk}收敛阶高于算法DNRTR. 由算法AADQN可知 进一步,由极限的性质可得 为了方便,记算法AADQN 步5 中的k=.由(38)以及(17)则有 本节给出一些数值例子来验证§2提出的算法1(AADQN)在求解无约束优化问题(1)时的高效性.通过与文献[1]中的算法DNRTR 在更方面性能指标进行详细对比.这些指标包括迭代次数(记为“IT”),消耗的CPU时间(记为“CPU”),梯度范数(记为“GN”)以及函数值(记为“VAL”).终止准则为GN=‖g(xk)‖2<10−6或迭代次数超过kmax=500,其中xk表示第k步迭代点.数值实验的机器环境为Intel(R)Core(TM) i7-2670QM,CPU 2.20GHZ,内存8GB的Windows10操作系统. 为了全面比较两个算法的综合性能,选择了无约束优化问题的10个不同测试函数,这些测试函数源于文献[25],其中10个不同的测试函数也充分地展现了其多样性和非线性程度.将这些测试函数的具体形式列在表1中,同时给出不同的初始点信息. 表1 测试函数 所有的数值测试结果在表2-4以及图1-2中展示. 表2-4中列出两种算法的收敛性对比结果.事实上,可以给出更多不同参数下的收敛性状况.本节给出当参数α=2,β=1,γ=1,δ=2,c=100的情形.从相关收敛性指标中,注意到VAL未必都会趋向于零,原因是有些测试函数并非在零处取得其最小值.在图1-图2中,显示了在不用维数下算法AADQN的迭代序列{xk}的梯度范数(GN)下降速度非常迅速,且明显优于算法DNRTR,特别是针对Pertured Quadratic函数维数较高(n=10000)情形,算法AADQN的迭代次数均小于30次,而算法DNRTR都超过了500次.这种高阶收敛的理论依据在定理3中已给出具体证明.同时在表2-表4中也注意到对于大部分测试函数,在计算成本方面,算法AADQN明显小于算法DNRTR. 图1 算法DNRTR 与AADQN 的收敛性轨迹, n=300,400 图2 算法DNRTR 与AADQN 的收敛性轨迹, n=5000,10000 表2 数值结果n=300 表3 数值结果n=300 表4 Pertured Quadratic 函数在不同维数情形下的数值结果 总而言之,两种方法均收敛到无约束优化问题(1)的解x∗.然而,无论从CPU时间与迭代次数,亦或者是GN与VAL,都明显说明了算法AADQN优于算法DNRTR.这也意味着算法AADQN 在求解无约束优化问题(1)时是可行且有效的. 本文基于对角拟牛顿更新,提出一个求解无约束优化问题的修正Aitken加速迭代算法.这种新思想的获得是源于在搜索方向更新时借助了对角矩阵,从而具有互相独立的“ 点对点”更新特性,因此易于考虑引入一些有效的加速技巧.算法的高阶收敛性优点在理论上得到验证.数值实验结果也进一步说明了,所提出的算法在求解无约束优化问题时是很有意义且非常高效的.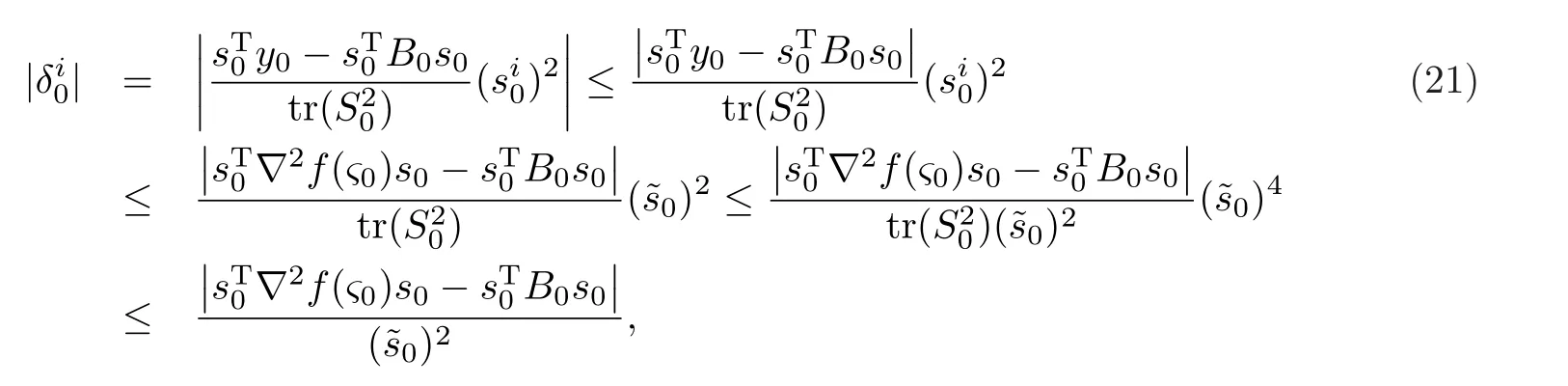



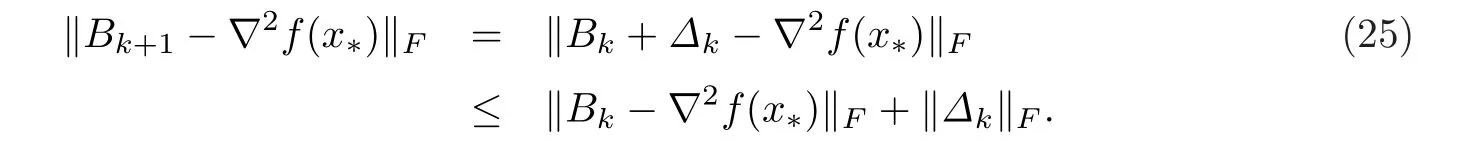




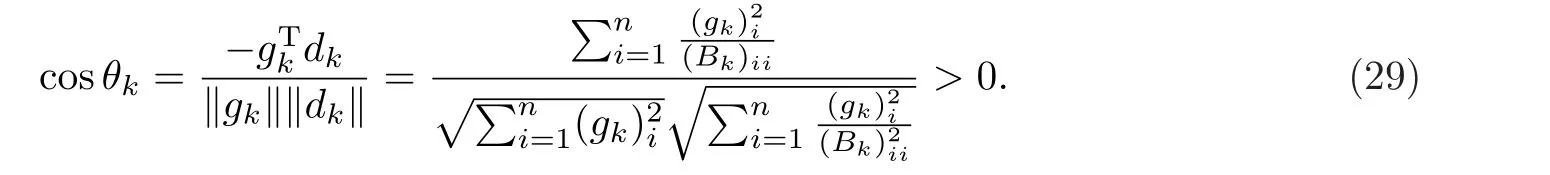

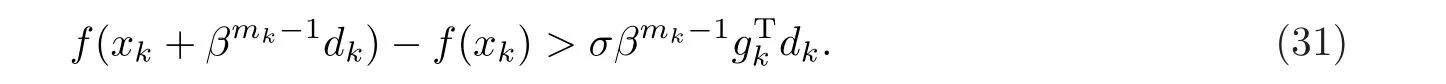
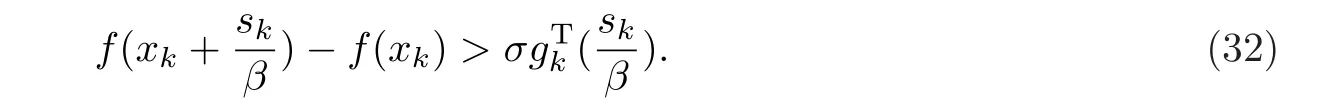


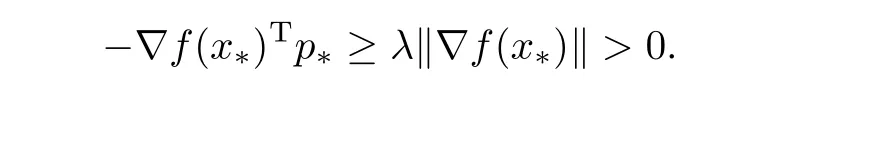


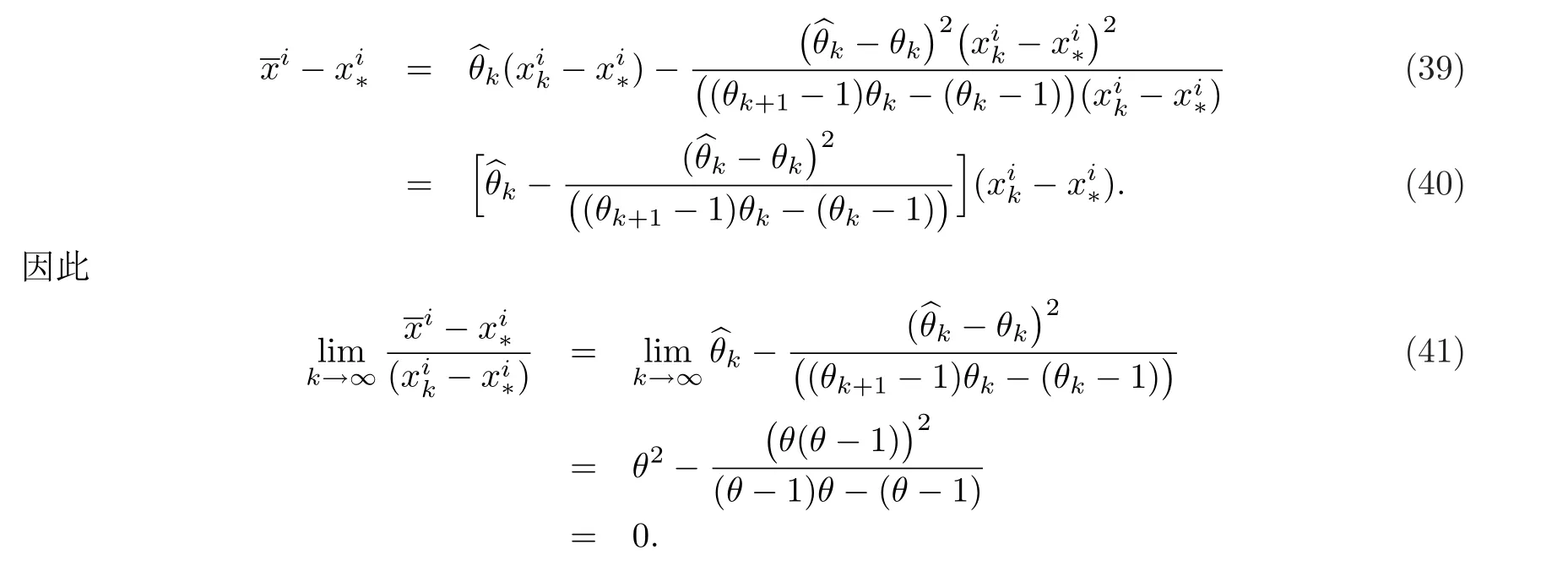
§3 数值实验





§4 结论

