一类具有时变系数的超线性抛物系统的渐近稳定性
郑 军∗何 莎
(1.西南交通大学 数学学院,四川成都 611756;2.蒙特利尔工学院 电气工程系,加拿大蒙特利尔H3T 1J4)
§1 引言
在晶体生长,金属浇铸和退火,固体气体反应系统,固体和流体力学,以及生物系统中出现的许多问题中,所涉及的输运反应现象通常用具有时变系数的抛物型偏微分方程来描述,例如[1-6].具有时变系数的抛物型偏微分方程解的适定性以及正则性理论已有广泛发展(如[7-9]).然而对于具有时变系数的抛物型偏微分方程解的稳定性研究还比较有限,例如[10-13]考察的对象仅是具有时变系数的线性抛物系统,其中[10-12]通过控制器设计,得到系统的稳定性,而[13]建立了系统的可观性.基于此,本文考察具有时变系数的超线性抛物型偏微分方程

的稳定性.其中Ω ⊂RN(N ≥1)为有界开区域,且边界∂Ω是C1-的,a ∈C(Ω ×R+;R≥0),c ∈C(Ω ×R+;R)均依赖于时间变量t,f ∈C(Ω ×R+×R;R)为非线性项,且存在a0,µi ∈C(R≥0;R≥0),i=1,2,···,n,及c0∈C(R≥0;R)使得


这里mi >1,i=1,2,···,n,n为正整数,R为实数集,R+为正实数集,R≥0为非负实数集.
对于(1) 中的方程,一个典型的形式为

其中c,µ1,µ2为连续函数,p,q >1且p≠q.当c,µ1不依赖于时间变量且µ2(t)≡0时,在不同条件下,已有大量文献利用Galerkin方法,或能量方法,或稳定性集和半群理论等方法,对(4)的解在有限时间的爆破性,或在小初值条件下系统的稳定性等进行探讨,现不再详述.然而,当c,µ1,µ2依赖于时间变量且µ2(t)/≡0时,对该类问题的稳定性或者爆破性质进行研究存在着较大困难.另外,如前所述,由于许多工程实际问题中,描述物理现象的经常是具有时变系数的超线性方程,且从控制角度考虑,必须要保证系统的稳定性(以及可控性,可观性,可测性等),因此,对具有时变系数的超线性抛物系统的稳定性进行研究具有十分重要的意义.
在一定程度上,证明抛物系统的稳定性可以归属于偏微分方程正则性理论研究的范畴,因此许多偏微分正则性方法可以应用于抛物系统稳定性理论,例如,可以通过以下几个基本思路对抛物系统稳定性进行探究:一是方程本身就具有较好的结构性质,如非线性项具有良好的“ 符号”特征(或单调性质),则可以证明具有非时变系数的抛物系统的稳定性,例如[14-15];二是通过控制器设计,可以保证具有时变系数的线性抛物系统的稳定性,例如[10-12];三是利用扰动的思想研究系统的稳定性,例如,当初值为零时,若0为系统的平衡点,则对于较小的初值,可以得到具有非时变系数的超线性抛物系统的稳定性,例如[16-17].值得一提的是,对于一些具有非时变系数的抛物系统,证明在大初值条件下解是爆破的,可以看作是思路三的逆向思维的体现,例如[9-16].
本文基于上述思路三,在小初值的条件下,为具有时变系数的超线性抛物系统(1)建立不同范数意义下的渐近稳定性.为了克服时变系数及多个超线性项为系统稳定性的建立带来的困难,本文将首先考察一个含时变系数的非线性常微分系统,并证明在小初值条件下,该微分系统是渐近稳定的,即后文的引理4.1.最后,利用Lyapunov方法,并应用引理4.1,可以证明,在小初值条件下,具有时变系数的超线性抛物系统(1)在不同范数意义下均是渐近稳定的.
尽管本文建立的是小初值前提下的超线性抛物系统(1)的渐近稳定性,但由于引理4.1可以应用于或推广到更为广泛的系统,因此,本文方法也适用于具有更为一般形式的偏微分系统,或者常微分系统,或者抽象形式的有限维或无限维系统(参见后文注4.1及注4.3),从而,本文所使用的方法对于考察非线性控制系统的稳定性或非线性偏微分方程的正则性具有一定启发意义.
§2 记号与常用不等式
记K:={γ:R≥0→R≥0|γ(0)=0,γ连续,严格递增},L:={γ:R≥0→R≥0|γ连续,严格递减,且,KL:={µ:R≥0×R≥0→R≥0|对于任意固定的t ∈R≥0,µ(·,t)∈K,对于任意固定的s ∈R+,µ(s,·)∈L}.
本文使用的函数空间的记号都是标准的,参见[9].记‖u‖q:=‖u‖Lq(Ω),∀q ∈[1,+∞],特别地,记‖u‖:=‖u‖L2(Ω),‖u‖1,q:=‖u‖W1,q(Ω),∀q ∈[1,+∞].未加特殊说明外,本文出现的C均表示为常数,各处可以取不同值;对于任意常数ε>0,C(ε)表示为依赖于ε的常数,各处可以取不同值.
引理2.1[18,p313,314,119]下列插值不等式成立.

引理2.2[18,p285,290]下列Sobolev不等式成立.

§3 主要结论
本文作如下假设.
(H1) 1≤N ≤2,1 (H2)N >2,2 (H3) 存在常数δ0∈[0,1)及M >0使得 其中CE为引理1.2中的Sobolev 嵌入常数. (H2’)N >2,2<2mi <2∗,i=1,2,···,n. (H3’) 在(H3)中,δ0=0,M=1. 当a,c,f,u0及∂Ω充分光滑且f满足Bernstein-Nagumo型条件时,对于任意T >0,由[7,§6,Chap.V]知,在[0,T]时间段,系统(1) 一定存在古典解(或强解),其估计式依赖于T.当a,c,f,u0及∂Ω正则性降低,且f满足Bernstein-Nagumo型条件时,则通过函数序列逼近技巧可知(1)一定存在弱解.另外,当f不满足Bernstein-Nagumo型条件,但a,c,f,u0及∂Ω有较好的正则性时,对于某个固定的常数T >0,在[0,T]时间段,(1)一定存在弱解,见[19].特别地,若存在p >N且p ≥2,使得弱解的W1,p-估计式关于t一致有界,则该弱解是全局的,见[19].因此,只要稍加条件,总可以保证系统(1)的古典解(或强解),或弱解的全局或局部存在性.由于本文重点在于说明系统(1)的渐近稳定性,因此,在不加强调的情况下,本文仅假设a,c,f是连续的及∂Ω是C1-的(见引言部分),同时不再对初值u0,f的正则性进行特别的说明,所谓的解也总是使得本文每个式子都有意义.本文主要结论如下. 定理3.1记u为超线性抛物系统(1)的解,下面结论成立. 为了证明定理3.1,先证明一个有用的结论,它可以用于判断具有多个非线性项的控制系统的渐近稳定性. 引理4.1设如下条件成立. 对于任意T >0,若y为定义在[0,T]上的非负,绝对连续函数,且几乎处处满足如下微分不等式 其中y0≥0,则对于任意ε ∈(0,1−k),一定存在常数r∗=r∗(ε)>0与函数βε ∈KL,使得当y0 注意到G(0)=0及对于任意的s ≥0,总有βε(s,0)=s.断言由(7)定义的βε为KL-函数.事实上,由于η(s),η−1(s)及G(t)均连续,并注意到,则βε(s,t)关于s与t均连续.由于η(s)与η−1(s)均严格单调递减,则对于固定的t,βε(s,t)关于s严格单调递增.由条件(i)及(7)可知,对于固定的s,.综上,由(7)定义的βε为KL-函数. 现令t∗=inf{t ∈[0,T]|y(t)≥r∗}.由于y(0)=y0 若t∗∈(0,T],则由t∗的定义知 从而由(5),(6)及条件(i)得 如果y0>0,由(8)可得 由η(s)的定义,并注意到η−1(s) 在[0,+∞)上单调递减,可得 如果y0=0,由(8)可知,y(t)在[0,t∗)上单调递减,从而对于任意t ∈[0,t∗)总有y(t)=0=βε(0,t)=βε(y0,t). 因此只要0≤y0 这是一个矛盾! 因此{t ∈[0,T]|y(t)≥r∗}=∅,即 进而,如上述过程可证明当y0 注4.1引理4.1的证明思想来源于[20,引理4.4].在文献[20]中,g2(t)α2(y)≡0,因此引理4.1是[20,引理4.4]在系统具有更多个非线性项的情形下的推广.并且,值得一提的是,Dini 导数意义下,引理4.1 的结论仍然成立. 定理3.1的证明首先,证明(i)中的结论.将(1)两边乘以u并积分,经过简单计算得 再利用结构性条件得 下面分两种情形进行讨论. 由引理2.1(i)得 由引理2.2(ii)及Young不等式得 由(9),(10)及(H3)得 由引理2.1(ii)得 由引理2.2(i),引理2.2(ii)及Young不等式得 注意到此时仍有 类似情形1可证得结论. 其次,证明(ii)中结论.采用(i)的证明方法.事实上,将(1)两边乘以Δu,再积分并整理得 注意到条件(H1)(或(H2’))总可以保证 由引理4.1可知:对于任意σ ∈(0,1),一定存在常数r∗=r∗(σ)>0,使得当‖∇u0‖2 推论3.1的证明只需注意到(13)与(14),并关于时间变量进行积分,则可以得到推论3.1的结论. 注4.3引理4.1可以用来处理更为广泛的非线性系统的稳定性,包括偏微分控制系统,常微分控制系统,以及具有抽象形式的有限维或无限维系统.例如,考察如下非线性常微分系统 首先注意到y=0满足方程(15a),故由比较原理可知,对于任意t ≥0,总有y ≥0.其次,注意到对于任意t ≥0,总有t ≤(1+t)ln(1+t),因此,为证明(15)的稳定性,只需证明下面系统的稳定性.(因为由比较原理知,0≤y ≤z) 本文首先证明了一类具有小初值与多个非线性项的时变系数常微分系统的渐近稳定性,在此基础上,获得了一类具有时变系数与小初值的超线性抛物系统在不同范数意义下的渐近稳定性.注意到本文所考察的具有时变系数的非线性常微分系统具有较为一般的形式,因此,本文的方法有望推广应用到更为广泛的非线性偏微分系统,以及其他控制系统.特别地,在下一个工作中,将利用本文引理与定理的证明思想,考察一类抽象形式的无限维控制系统的稳定性.

§4 主要结论的证明






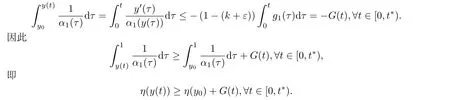







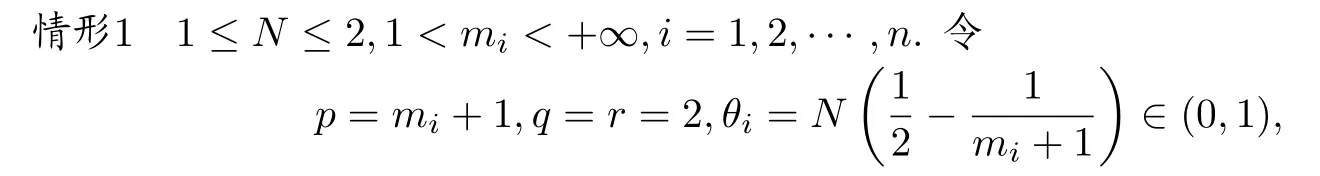







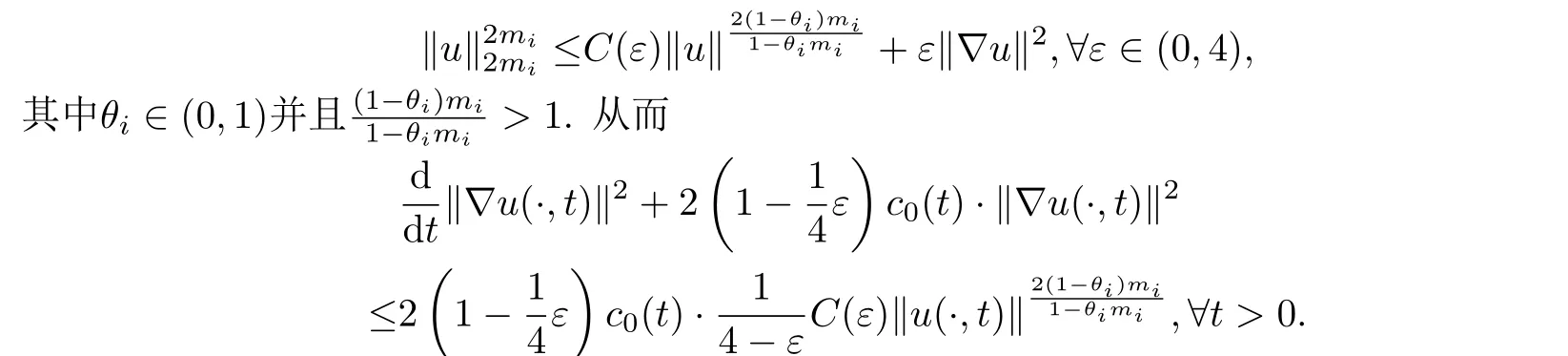
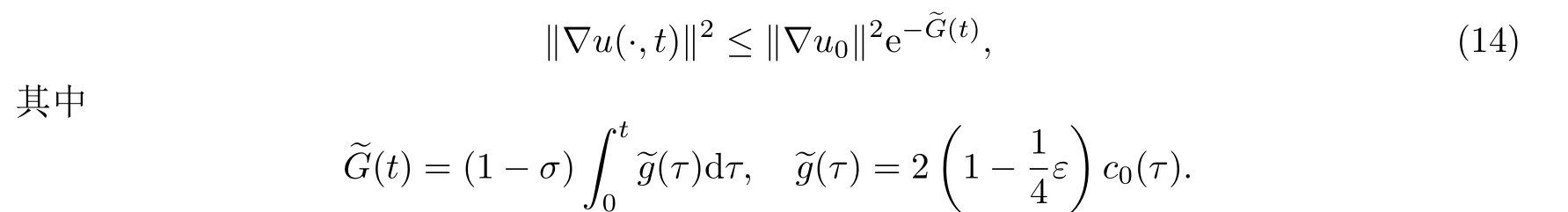


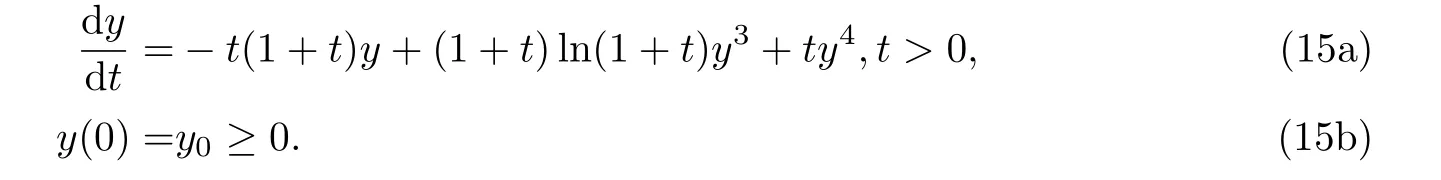

§5 结束语

